جک نایف و بوت استرپ (Jackknife and Bootstrap) روش های بازنمونه گیری — به زبان ساده

به منظور برآورد پارامترهای جامعه آماری، از یک نمونه آماری استفاده میکنیم. گاهی حجم نمونه برای برآورد چنین پارامتری کم است. برای افزایش دقت و همچنین برآورد خطای برآوردگر پارامتر جامعه، از روشهای «بازنمونهگیری» (Re-sampling) استفاده میشود. «بوت استرپ» (Bootstrap) و «جک نایف» (Jackknife)، از جمله روشهای پرکاربرد در این زمینه هستند. برای آشنایی بیشتر با مفهوم نمونهگیری و بازنمونهگیری بهتر است مطلب نمونهگیری و بازنمونهگیری آماری (Sampling and Re-sampling) --- به زبان ساده را مطالعه کنید. هر دو روش جک نایف و بوت استرپ، در گروه محاسبات ناپارامتری قرار داشته و برای برآورد «خطای استاندارد» (Standard Error) و «فاصله اطمینان» (Confidence Interval) به کار میروند.
روش جک نایف توسط «موریس کوئینل» (Maurice Quenouille) آمارشناس انگلیسی در سال 1949 معرفی شد ولی بعدها «بردلی افرون» (Bradley Efron) دانشمند آمریکایی، آن را در سال 1979 توسعه داد و روش بوت استرپ را معرفی کرد.

در معنی لغت، جک نایف به معنی چاقوی ضامندار چند کاره است. در روش جک نایف نیز به کمک چنین چاقویی، بازنمونهگیری از نمونه موجود تهیه شده و برآورد توسط آن انجام میشود.
همچنین بوت استرپ به معنی بند پوتین یا چکمه است، که در انتهای پوتین قرار گرفته و کار پوشیدن آن را سادهتر میکند. افرون به دلیل راحتی محاسبات در این روش برای محاسبه خطای برآوردگرها، این نام را انتخاب کرده است.

روش جک نایف
فرض کنید، برآوردگر پارامتر باشد. اگر iامین مشاهده از این نمونه را خارج کنیم، برآوردگر حاصل از باقیمانده اعضای نمونه تصادفی را با نشان میدهیم. حال برآوردگر جکنایف برای پارامتر جامعه را به صورت زیر معرفی میکنیم:
در نتیجه میتوان مراحل مربوط به محاسبه برآوردگر جک نایف را به شکل زیر در نظر گرفت:
- تهیه یک نمونه تصادفی به حجم n از جامعه آماری
- خارج کردن عنصر iام از نمونه اصلی و انتخاب n-1 مشاهده باقیمانده
- محاسبه برآوردگر مربوط به پارامتر جامعه آماری توسط این نمونه n-1تایی ( )
- تکرار مراحل ۲ و ۳ برای i=1,2,...,n.
- محاسبه میانگین مقدارهای بدست آمده از مرحله ۳ به عنوان برآوردگر جکنایف پارامتر جامعه آماری ()
اهمیت این روش در امکان محاسبه خطای برآوردگر در زمانی است که توزیع برآوردگر پارامتر موجود نباشد. برای مثال در بیشتر مواقع محاسبه خطای برآوردگر برای پارامترهایی مانند صدکهای جامعه آماری به راحتی امکان پذیر نیست.
اگر برآوردگر برای چنین پارامتری باشد، خطای این برآوردگر را میتوان از طریق واریانس ها بدست آورد. در نتیجه خواهیم داشت:
مثال ۱
فرض کنید چهار مشاهده ، نمونه تصادفی را تشکیل میدهند و . به این ترتیب مقدار میانگین این چهار مشاهده برابر است با:
حال چهار برآوردگر حاصل از روش جکنایف طبق جدول زیر بدست میآید:
| دادهها | 2,3,4 | 1,3,4 | 1,2,4 | 1,2,3 |
| برآوردگر (میانگین) |
در نتیجه برآوردگر جکنایف برابر است با:
و واریانس برای این برآوردگر نیز برابر است با:
البته در این مثال واریانس برآوردگر برابر است با 0.104 که در مقایسه با برآوردگر جک نایف کوچکتر است ولی اهمیت روش جک نایف در مواردی است که توزیع برآوردگر و در نتیجه واریانس آن نامشخص است. برای روشن شدن این موضوع میتوانید به مثال ۴ توجه کنید.
برآوردگر اریب-اصلاح شده جک نایف
به کمک روش جکنایف میتوان اریبی برآوردگر را نیز محاسبه کرد. برآورد اریبی به روش جکنایف برای برآوردگر برابر است با:
در نتیجه برآوردگر «اریب-اصلاح شده جک نایف» (Bias Corrected Jackknife) برابر خواهد بود با:
با توجه به مثال ۱ برآوردگر جک نایف اصلاح شده، برابر است با 2.5 و میزان اریبی آن نیز صفر محاسبه میشود.
روش بوت استرپ
این روش در گروه روشهای آمار ناپارامتری و تکنیکهای بازنمونهگیری طبقهبندی میشود و به منظور برآورد پارامتر جامعه آماری با استفاده از نمونهگیری با جایگذاری به کار میرود. بوتاسترپ همچنین برای محاسبه فاصله اطمینان برای برآوردگر کاربرد دارد. فرض کنید میخواهید در یک مسئله یادگیری ماشین، مهارت مدل تولید شده را اندازهگیری کنید. برای این کار با استفاده از روش بوتاسترپ میتوان یک فاصله اطمینان ایجاد کرد و برای پیشبینی دادههای جدید از آن کمک گرفت.
همانطور که دیده شد، در روش جک نایف برای n مشاهده، n زیرنمونه به اندازه n-1 برای برآورد پارامتر جامعه آماری ایجاد شد. ولی در روش بوت استرپ زیرنمونهها، بوسیله بازنمونهگیری با جایگذاری از نمونه اصلی تولید میشوند. با توجه به اینکه تعداد نمونه اصلی برابر با n است میتوان بینهایت زیرنمونه با اندازه n با جایگذاری ایجاد کرد. در روش بوت استرپ تعداد بازنمونهگیری با و تعداد مشاهدات در هر زیرنمونه نیز با مشخص میشود. واضح است که و ممکن است از n بزرگتر، مساوی یا کوچکتر باشند زیرا نمونهگیری با جایگذاری است و در حقیقت حجم نمونه اصلی را میتوان بسیار بزرگ در نظر گرفت.
مراحل روش بوت استرپ را میتوان به صورت زیر معرفی کرد:
- تعیین تعداد زیرنمونهها
- تعیین حجم زیرنمونهها
- انتخاب یک مشاهده از نمونه اصلی و قرار دادن آن در زیرنمونه
- تکرار مرحله ۲ تا رسیدن به حجم زیرنمونه (روش نمونهگیری با جایگذاری)
- محاسبه برآوردگر مربوط به پارامتر جامعه آماری با استفاده از زیرنمونه
- تکرار مراحل ۳ تا ۵ به تعداد به منظور بدست آوردن همین تعداد برآوردگر
- محاسبه میانگین برآوردگرهای محاسبه شده در مرحله 6
مثال ۲
شبه کد مربوط به برآورد میانه جامعه آماری براساس یک مجموعه داده به کمک روش بوتاسترپ در این مثال بررسی میشود. فرض کنید مجموعه n مشاهده از یک نمونه تصادفی باشد. هدف برآورد میانه برای این دادهها است. میانه این نمونه تصادفی میتواند برآوردی برای میانه جامعه آماری باشد.
|
T= mean(TBoot) |
در سطر اول شبه کد، مجموعه داده x، معرفی شده است. سپس برداری با نام TBoot به طول برای قرارگیری میانههای حاصل از زیرنمونههای تولید شده در بوت استرپ، ایجاد و مراحل بوت استرپ آغاز میشود.
در یک حلقه تکرار (Loop)، بازنمونهگیریها انجام شده و میانه حاصل از آن زیرنمونهها در بردار TBoot ثبت میشود. در انتها نیز به منظور محاسبه برآورد میانه دادهها به روش بوتاسترپ، میانگین بردار TBoot در متغیر T ثبت شده. همچنین خطای برآوردگر بوتاسترپ، با محاسبه انحراف استاندار مقدارهای بردار TBoot به عنوان خروجی در متغیر se قرار گرفته است.
مثال ۳
در این مثال با استفاده از شبه کد نوشته شده در مثال ۲ برآورد میانه را برای وزن ۱۰ بسته به کمک روش بوت استرپ بررسی میکنیم.
اطلاعات مربوط به وزن این بستهها در جدول زیر قرار داد. محقق میخواهد میانه و واریانس میانه وزن این بستهها را محاسبه کند.
| بسته | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| وزن | 191 | 180 | 160 | 220 | 297 | 93 | 302 | 215 | 243 | 171 |
با انتخاب و عمل بوتاسترپ آغاز میشود. در مرحله اول نتیجه بازنمونهگیری با جایگذاری به صورت زیر است.
| بسته | 1 | 1 | 3 | 3 | 4 | 5 | 6 | 6 | 6 | 9 |
| وزن | 191 | 191 | 160 | 160 | 220 | 297 | 93 | 93 | 93 | 243 |
میانه در این حالت برابر با 175.5 است. در مرحله دوم نیز نتایج طبق جدول زیر است:
| بسته | 2 | 5 | 6 | 6 | 6 | 6 | 7 | 7 | 9 | 10 |
| وزن | 180 | 297 | 93 | 93 | 93 | 93 | 302 | 302 | 243 | 171 |
میانه در این حالت نیز برابر با 175.5 است. در مرحله سوم نیز نتایج طبق جدول زیر است:
| بسته | 1 | 1 | 3 | 4 | 5 | 5 | 7 | 8 | 8 | 10 |
| وزن | 191 | 191 | 160 | 220 | 297 | 297 | 302 | 215 | 215 | 171 |
میانه در این مرحله برابر با ۲۱۵ است. این کار به تعداد تکرار میشود و جدول و نمودار فراوانی مربوط به مقدارهای میانهها ترسیم میشود.
| حدود رده | نماینده رده | فراوانی |
| 160-170 | 165 | 2 |
| 170-180 | 175 | 6 |
| 180-190 | 185 | 7 |
| 190-200 | 195 | 6 |
| 200-210 | 205 | 8 |
| 210-220 | 215 | 14 |
| 220-230 | 225 | 3 |
| 230-240 | 235 | 4 |
برای پیدا کردن میانه به روش بوتاسترپ کافی است میانگین وزنی (با وزن فراوانی ردهها) مقدارهای نماینده ردهها را محاسبه کنیم.
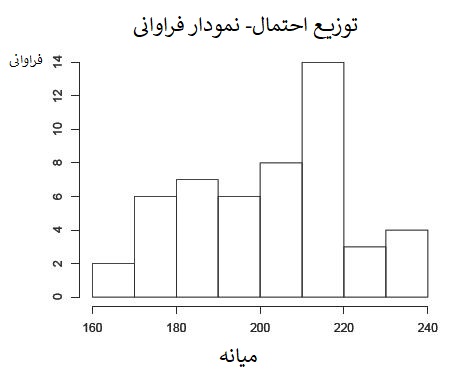
واریانس این مقدارها نیز برابر با 41241 است. در نتیجه خطای برآورد برابر است با:
مثال ۴
با استفاده از بسته bootstrap در نرمافزار R نیز امکان استفاده از روشهای برآوردیابی جک نایف و بوت استرپ وجود دارد. در زیر کد مربوط به برآورد صدک 65ام دادههای توزیع نرمال آورده شده است.
library(bootstrap)
set.seed(12345)
x = rnorm(10)
p65 = function(x){quantile(x, .65)}
bp65=bootstrap(x,nboot = 100,p65)
jp65=jackknife(x,p65)
mean(bp65$thetastar)
mean(jp65$jack.values)
sd(bp65$thetastar)
sd(jp65$jack.values)
دستور اول فراخوانی bootstrap از بستههای (Packages) زبان آماری R را به عهده دارد. خط دوم کد نیز به منظور یکسان سازی نتایج حاصل از تولید اعداد تصادفی نوشته شده. خط سوم کد نیز وظیفه تولید ۱۰ عدد تصادفی از توزیع نرمال را دارد. همچنین در خط چهارم، تابعی که برای محاسبه صدک ۶۵ لازم است نوشته شده. در خط پنجم و ششم نیز توابع مربوط به برآورد بوتاسترپ و جکنایف صدک ۶۵ام با استفاده از دادههای x تعریف شدهاند.
در خط هفتم و هشتم نیز میانگین برآوردگرهای حاصل از هر دو روش ارائه شدهاست. نتایج حاصل از این برنامه برای روش بوت استرپ برابر با 0.2414 و برای روش جک نایف نیز 0.3660 خواهد بود. این دو عدد بیانگر برآورد صدک ۶۵ام از یک جامعه نرمال با میانگین ۰ و واریانس ۱ است. در انتها نیز خطای برآوردگرها در هر دو روش استخراج شده که برابر با 0.3928 و 0.288 خواهد بود.
اگر به فراگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های Minitab
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش روش های نمونه برداری و بازرسی در کنترل کیفیت
- نمونهگیری و بازنمونهگیری آماری (Sampling and Re-sampling) --- به زبان ساده
- مفاهیم آماری – شاخصهای توصیفی
- توزیع فراوانی – به زبان ساده
- جامعه آماری — انواع داده و مقیاسهای آنها
- مفاهیم آماری – آمار و جامعه آماری – به زبان ساده
^^











سلام خسته نباشید
من سمیناری در رابطه با برآورد خطای استاندارد جک نایف و بوت استرپ و فواصل اطمینان مربوط به اون رو قراره ارایه بدم ولی هیچ مطلب و کتابی نمی تونم در رابطه باهاش پیدا کنم تموم مطالب و مقالات زبان اصلی هست…
اگه میشه یه سری کتاب و مطلب در این باره معرفی کنید که زبان اصلی نباشه …
ممنون