برنامه تشخیص درخت بودن یک گراف – راهنمای کاربردی

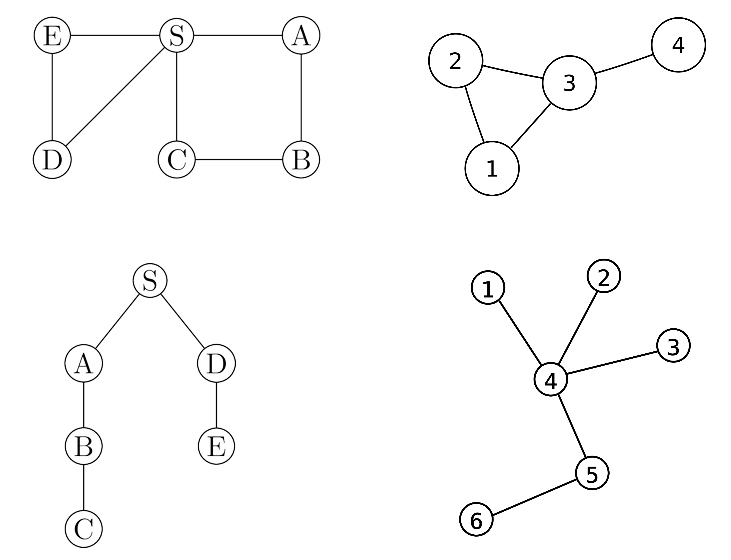
در این مطلب، برنامه تشخیص درخت بودن یک گراف در زبان‌های برنامه‌نویسی گوناگون شامل ++C، «پایتون» (Python) و «جاوا» (Java) ارائه شده است. در واقع، هدف نوشتن تابعی است که یک گراف بدون جهت را دریافت کرده و بررسی کند که آیا درخت است یا نه. در صورتی که گراف یک درخت بود «مقدار یک» و در غیر این صورت، «مقدار صفر» را بازگرداند. برای مثال، گراف زیر یک درخت است.

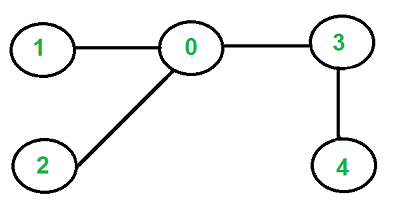
اما، گراف زیر یک درخت نیست.

یک گراف بدون جهت، در صورتی درخت است که مشخصات زیر را داشته باشد:

1. هیچ دوری نداشته باشد.
2. گراف هم‌بند باشد.

برای یک گراف بدون جهت، می‌توان از الگوریتم‌های «جستجوی اول سطح» (Breadth-First Search | BFS) یا «جستجوی اول عمق» (Depth-First Search | DFS) برای تشخیص وجود دو ویژگی بالا استفاده کرد. شایان ذکر است، برای مطالعه بیشتر پیرامون گراف و درخت، مطالعه مطالب «گراف — تعاریف و انواع آن به زبان ساده» و «درخت در گراف — به زبان ساده» توصیه می‌شود.

روش شناسایی دور در یک گراف بدون جهت

همانطور که پیش‌تر بیان شد، برای تعیین درخت بودن یا نبودن یک گراف بدون جهت، می‌توان از الگوریتم‌های BFS یا DFS استفاده کرد. برای هر یک از راس‌های بازدید شده v، اگر یک راس هم‌جوار u وجود داشته باشد که پیش از این بازدید شده باشد و u والد v نباشد، یک دور در گراف وجود دارد. اگر چنین راس هم‌جواری برای هیچ یک از راس‌ها یافت نشود، هیچ دوری در گراف وجود ندارد.

روش شناسایی هم‌بندی در یک گراف بدون جهت

از آنجا که گراف بدون جهت است، می‌توان کار را با استفاده از الگوریتم BFS یا DFS و از هر راسی آغاز کرد و بررسی کرد که آیا همه راس‌ها دسترسی پذیر هستند یا خیر. در صورتی که همه راس‌ها دسترسی پذیر باشند، گراف هم‌بند است و در غیر این صورت هم‌بند نیست.

برنامه تشخیص درخت بودن یک گراف در ++C

برنامه تشخیص درخت بودن یک گراف در جاوا

برنامه تشخیص درخت بودن یک گراف در پایتون

پیاده‌سازی و انجام عملیات مختلف مربوط به گراف در پایتون هم دارای اصول و قواعد یکسانی است. با این تفاوت که هر زبان سینتکس و قواعد گرامری مخصوص به خود را دارد. در زیر کدهای مربوط به تشخیص درخت بودن گراف را در این زبان مشاهده می‌کنید.

خروجی

Graph is Tree
Graph is not Tree

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^