فرادرس
الگوریتم بازی مار و پله همراه با کد — به زبان ساده
بازی مار و پله (Snakes and Ladders)، یک بازی باستانی هندی است که اکنون یک بازی کلاسیک جهانی محبوب محسوب می‌شود. این بازی قابل انجام بین دو یا تعداد بیشتری بازیکن است. صفحه بازی مار و پله، شطرنجی است؛ در این بازی، در برخی از خانه‌ها نردبان‌هایی وجود دارد که فرد را به خانه‌های بالاتر می‌رساند و در بعضی از خانه‌ها، مارهایی وجود دارد که فرد را اصطلاحا نیش می‌زنند و به خانه‌های پایین‌تری انتقال می‌دهند (جایی که دم مار در آن قرار دارد). بازی به این صورت انجام می‌شود که هر بازیکن تاس می‌اندازد و با توجه به عددی که می‌آید، تعداد خانه‌هایی را به جلو حرکت می‌کند. بسته به عدد تاس، ممکن است فرد در یک خانه عادی، دارای نربان و یا دارای مار قرار بگیرد. در «مساله مار و پله» (Snake and Ladder Problem)، هدف پیدا کردن کمترین تعداد دفعات پرتاب تاس لازم برای رسیدن به مقصد (آخرین خانه در صفحه شطرنجی) از مبدا (اولین خانه) است. این مساله کمی با بازی تخته‌ای متداول مار و پله که افراد بازی می‌کنند متفاوت است و در آن، بازیکن بر عددی که در پرتاب تاس به دست می‌آید کنترل دارد و باید اعدادی را پیدا کند که با کمترین تعداد پرتاب تاس به خانه نهایی برسد. در ادامه، الگوریتم بازی مار و پله (در واقع الگوریتم لازم برای حل این مساله) ارائه و پیاده‌سازی آن در زبان‌های برنامه‌نویسی «پایتون» (Python)، «جاوا» (Java)، «سی‌پلاس‌پلاس» (++C) و «سی‌شارپ» (#C) انجام شده است.
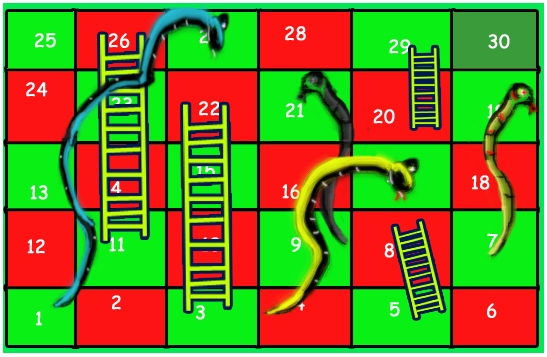
الگوریتم بازی مار و پله
برای مثال، در صفحه بازی موجود در تصویر بالا، تعداد پرتاب‌های تاس لازم برای رسیدن از خانه ۱ به خانه ۳۰ برابر با سه است. گام‌های زیر برای آنکه بازیکن با سه پرتاب تاس به نتیجه برسد انجام می‌شود.
- ابتدا تاس دو انداخته می‌شود تا بازیکن از خانه یک به خانه سه برود و با استفاده از نردبان به خانه ۲۲ برسد.
- سپس، تاس ۶ انداخته می‌شود تا فرد از خانه ۲۲ به خانه ۲۸ برسد.
- در نهایت، با انداختن تاس ۲، بازیکن به خانه ۳۰ (مقصد نهایی) می‌رسد.
برخی از دیگر راهکارهای موجود برای حل مساله مار و پله (با کمترین تعداد پرتاب تاس) عبارتند از: (2, 2, 6)، (2, 4, 4) و (2, 3, 5).
ایده موجود برای حل این مساله در حالت کلی آن است که صفحه بازی به صورت یک گراف جهت‌دار در نظر گرفته شود. اکنون، مساله یافتن کوتاه‌ترین مسیر در گراف است. هر «راس» (Vertex) از گراف، دارای «یالی» (Edge) به شش راس بعدی است؛ اگر راس‌های بعدی دارای نردبان یا مار نباشند. اگر هر یک از شش راس دارای مار یا نردبان باشند، یال از راس کنونی به راس بالای نردبان یا دم مار متصل می‌شود.
با توجه به اینکه همه یال‌ها دارای وزن‌های برابری هستند، می‌توان کوتاه‌ترین مسیر را با استفاده از «جستجوی اول عمق» (Breadth First Search) کشف کرد. در ادامه، پیاده‌سازی ایده بالا با استفاده از زبان‌های برنامه‌نویسی گوناگون انجام شده است. ورودی با دو چیز نمایش داده شده است: N که تعداد خانه‌های صفحه بازی است و آرایه [move[0…N-1 با اندازه N. یک ورودی [move[i برابر با ۱- است اگر هیچ مار یا نردبانی از i وجود نداشته باشد؛ در غیر این صورت، [move[i حاوی اندیس سلول مقصد برای مار یا نردبان در i است.
پیاده سازی الگوریتم بازی مار و پله در ++C
// C++ program to find minimum number of dice throws required to
// reach last cell from first cell of a given snake and ladder
// board
#include<iostream>
#include <queue>
using namespace std;
// An entry in queue used in BFS
struct queueEntry
{
int v; // Vertex number
int dist; // Distance of this vertex from source
};
// This function returns minimum number of dice throws required to
// Reach last cell from 0'th cell in a snake and ladder game.
// move[] is an array of size N where N is no. of cells on board
// If there is no snake or ladder from cell i, then move[i] is -1
// Otherwise move[i] contains cell to which snake or ladder at i
// takes to.
int getMinDiceThrows(int move[], int N)
{
// The graph has N vertices. Mark all the vertices as
// not visited
bool *visited = new bool[N];
for (int i = 0; i < N; i++)
visited[i] = false;
// Create a queue for BFS
queue<queueEntry> q;
// Mark the node 0 as visited and enqueue it.
visited[0] = true;
queueEntry s = {0, 0}; // distance of 0't vertex is also 0
q.push(s); // Enqueue 0'th vertex
// Do a BFS starting from vertex at index 0
queueEntry qe; // A queue entry (qe)
while (!q.empty())
{
qe = q.front();
int v = qe.v; // vertex no. of queue entry
// If front vertex is the destination vertex,
// we are done
if (v == N-1)
break;
// Otherwise dequeue the front vertex and enqueue
// its adjacent vertices (or cell numbers reachable
// through a dice throw)
q.pop();
for (int j=v+1; j<=(v+6) && j<N; ++j)
{
// If this cell is already visited, then ignore
if (!visited[j])
{
// Otherwise calculate its distance and mark it
// as visited
queueEntry a;
a.dist = (qe.dist + 1);
visited[j] = true;
// Check if there a snake or ladder at 'j'
// then tail of snake or top of ladder
// become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.push(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
// Driver program to test methods of graph class
int main()
{
// Let us construct the board given in above diagram
int N = 30;
int moves[N];
for (int i = 0; i<N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
cout << "Min Dice throws required is " << getMinDiceThrows(moves, N);
return 0;
}
پیاده سازی الگوریتم بازی مار و پله در پایتون
# Python3 program to find minimum number
# of dice throws required to reach last
# cell from first cell of a given
# snake and ladder board
# An entry in queue used in BFS
class QueueEntry(object):
def __init__(self, v = 0, dist = 0):
self.v = v
self.dist = dist
'''This function returns minimum number of
dice throws required to. Reach last cell
from 0'th cell in a snake and ladder game.
move[] is an array of size N where N is
no. of cells on board. If there is no
snake or ladder from cell i, then move[i]
is -1. Otherwise move[i] contains cell to
which snake or ladder at i takes to.'''
def getMinDiceThrows(move, N):
# The graph has N vertices. Mark all
# the vertices as not visited
visited = [False] * N
# Create a queue for BFS
queue = []
# Mark the node 0 as visited and enqueue it
visited[0] = True
# Distance of 0't vertex is also 0
# Enqueue 0'th vertex
queue.append(QueueEntry(0, 0))
# Do a BFS starting from vertex at index 0
qe = QueueEntry() # A queue entry (qe)
while queue:
qe = queue.pop(0)
v = qe.v # Vertex no. of queue entry
# If front vertex is the destination
# vertex, we are done
if v == N - 1:
break
# Otherwise dequeue the front vertex
# and enqueue its adjacent vertices
# (or cell numbers reachable through
# a dice throw)
j = v + 1
while j <= v + 6 and j < N:
# If this cell is already visited,
# then ignore
if visited[j] is False:
# Otherwise calculate its
# distance and mark it
# as visited
a = QueueEntry()
a.dist = qe.dist + 1
visited[j] = True
# Check if there a snake or ladder
# at 'j' then tail of snake or top
# of ladder become the adjacent of 'i'
a.v = move[j] if move[j] != -1 else j
queue.append(a)
j += 1
# We reach here when 'qe' has last vertex
# return the distance of vertex in 'qe
return qe.dist
# driver code
N = 30
moves = [-1] * N
# Ladders
moves[2] = 21
moves[4] = 7
moves[10] = 25
moves[19] = 28
# Snakes
moves[26] = 0
moves[20] = 8
moves[16] = 3
moves[18] = 6
print("Min Dice throws required is {0}".
format(getMinDiceThrows(moves, N)))
# This code is contributed by Ajitesh Pathak
پیاده سازی الگوریتم بازی مار و پله در جاوا
// Java program to find minimum number of dice
// throws required to reach last cell from first
// cell of a given snake and ladder board
import java.util.LinkedList;
import java.util.Queue;
public class SnakesLadder
{
// An entry in queue used in BFS
static class qentry
{
int v;// Vertex number
int dist;// Distance of this vertex from source
}
// This function returns minimum number of dice
// throws required to Reach last cell from 0'th cell
// in a snake and ladder game. move[] is an array of
// size N where N is no. of cells on board If there
// is no snake or ladder from cell i, then move[i]
// is -1 Otherwise move[i] contains cell to which
// snake or ladder at i takes to.
static int getMinDiceThrows(int move[], int n)
{
int visited[] = new int[n];
Queue<qentry> q = new LinkedList<>();
qentry qe = new qentry();
qe.v = 0;
qe.dist = 0;
// Mark the node 0 as visited and enqueue it.
visited[0] = 1;
q.add(qe);
// Do a BFS starting from vertex at index 0
while (!q.isEmpty())
{
qe = q.remove();
int v = qe.v;
// If front vertex is the destination
// vertex, we are done
if (v == n - 1)
break;
// Otherwise dequeue the front vertex and
// enqueue its adjacent vertices (or cell
// numbers reachable through a dice throw)
for (int j = v + 1; j <= (v + 6) && j < n; ++j)
{
// If this cell is already visited, then ignore
if (visited[j] == 0)
{
// Otherwise calculate its distance and
// mark it as visited
qentry a = new qentry();
a.dist = (qe.dist + 1);
visited[j] = 1;
// Check if there a snake or ladder at 'j'
// then tail of snake or top of ladder
// become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.add(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
public static void main(String[] args)
{
// Let us construct the board given in above diagram
int N = 30;
int moves[] = new int[N];
for (int i = 0; i < N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
System.out.println("Min Dice throws required is " +
getMinDiceThrows(moves, N));
}
}
خروجی:
Min Dice throws required is 3
پیچیدگی زمانی راهکار بالا از درجه (O(N است؛ زیرا هر سلول تنها یک‌بار به «صف» (Queue) اضافه و کم می‌شود و یک فرایند معمول افزودن به صف یا حذف کردن از آن از درجه زمانی (O(1 است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان داده‌ها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
^^
سلام وقت بخیر و خسته نباشید به شما استاد گرامی
اگه امکانش باشه با بیسیک فور اندروید هم کدش رو قرار بدین
با تشکر