گراف قویا همبند و برنامه تشخیص آن — راهنمای کاربردی

در این مطلب، روش نوشتن برنامه‌ای که تشخیص می‌دهد یک گراف قویا همبند است یا خیر، مورد بررسی قرار گرفته است. همچنین، پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C، «جاوا» (Java) و «پایتون» (Python) انجام شده است. فرض می‌شود یک گراف جهت‌دار به عنوان ورودی به برنامه داده شده است. هدف آن است که برنامه بررسی و مشخص کند که آیا گراف قویا هم‌بند است یا خیر. یک گراف جهت‌دار، قویا هم‌بند است اگر مسیری بین هر دو جفت از راس‌های آن وجود داشته باشد. برای مثال، گرافی که در تصویر زیر آمده، قویا هم‌بند محسوب می‌شود.

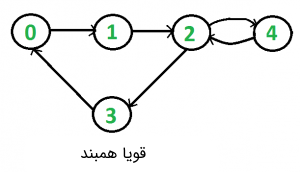
انجام چنین کاری در گراف غیرجهت‌دار آسان است. در این راستا، کافی است که پیمایش «جستجوی اول سطح» (Breadth-First Search | BFS) و «جستجوی اول عمق» (Depth-First Search | DFS) با آغاز از هر راسی انجام شود. اگر در پیمایش BFS یا DFS، همه راس‌ها مشاهده شدند، گراف غیر جهت‌دار همبند است. این رویکرد برای گراف‌های جهت‌دار پاسخگو نیست. برای مثال، گراف زیر قویا همبند نیست. اگر پیمایش DFS یا BFS با شروع از راس صفر انجام شود، می‌توان به همه راس‌ها رسید، اما اگر از هر راس دیگری آغاز شود، نمی‌توان به همه راس‌ها رسید.

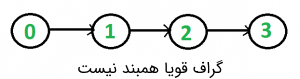
یک ایده ساده آن است که از همه الگوریتم‌های کوتاه‌ترین مسیرها مانند پیدا کردن «بستار تعدی» (Transitive Closure) گراف یا «الگوریتم فلوید-وارشال» (Floyd Warshall) استفاده شود. پیچیدگی زمانی این روش، از درجه (O(v³ است. همچنین، می‌توان DFS را به تعداد V مرتبه با آغاز از هر راسی انجام داد. اگر DFS همه راس‌ها را ملاقات نکرد، گراف قویا همبند نیست. این الگوریتم، ((O(V*(V+E زمان می‌برد که مشابه با بستار تعدی برای گراف چگال است.

یک ایده بهتر، استفاده از الگوریتم «اجزای قویاً هم‌بند» (Strongly Connected Components | SCC) است. می‌توان همه SCC‌ها را در زمان (O(V+E پیدا کرد. اگر تعداد SCC‌ها برابر با یک باشد، گراف قویا هم‌بند است. الگوریتم SCC پس از پیدا کردن همه SCC‌ها، دیگر کاری انجام نمی‌دهد. در ادامه، الگوریتم ساده و مبتنی بر DFS «کساراجو» (Kosaraju) ارائه شده است که دو پیمایش در گراف انجام و تشخیص می‌دهد که گراف قویا همبند است یا خیر. روش کار این الگوریتم، در ادامه بیان شده است.

1. همه راس‌ها را با «ملاقات نشده» مقداردهی اولیه کن.
2. پیمایش DFS گراف را با شروع از هر راس دلخواه v آغاز کن. اگر در پیمایش DFS همه راس‌ها ملاقات نشدند، false را بازگردان.
3. همه یال‌ها را معکوس کن (یا ترانهاده یا معکوس گراف را پیدا کن)
4. همه راس‌ها را در گراف معکوس شده با عنوان «ملاقات نشده» علامت‌گذاری کن.
5. پیمایش DFS گراف معکوس را از همان راس v (که در گام ۲ از آن استفاده شد) آغاز کن. اگر پیمایش DFS همه راس‌ها را ملاقات نکرد، مقدار false را بازگردان. در غیر این صورت، مقدار true را بازگردان.

ایده آن است که اگر همه گره‌ها از راس v دسترسی‌پذیر باشند، و هر گره‌ای بتواند به v برسد، گراف قویا هم‌بند است. در گام ۲، بررسی می‌شود که همه راس‌ها از راس v دسترسی‌پذیر هستند. در گام ۴، بررسی می‌شود که آیا می‌توان از همه راس‌ها به راس v رسید (در گراف معکوس، اگر همه راس‌ها از راس v دسترسی‌پذیر باشند، همه راس‌ها می‌توانند در گراف اصلی به راس v برسند). پیاده‌سازی الگوریتم بالا، در ادامه در زبان‌های برنامه‌نویسی گوناگون ارائه شده است.

برنامه تشخیص گراف قویا همبند در ++C

// C++ program to check if a given directed graph is strongly  
// connected or not 
#include <iostream> 
#include <list> 
#include <stack> 
using namespace std; 
  
class Graph 
{ 
    int V;    // No. of vertices 
    list<int> *adj;    // An array of adjacency lists 
  
    // A recursive function to print DFS starting from v 
    void DFSUtil(int v, bool visited[]); 
public: 
    // Constructor and Destructor 
    Graph(int V) { this->V = V;  adj = new list<int>[V];} 
    ~Graph() { delete [] adj; } 
  
    // Method to add an edge 
    void addEdge(int v, int w); 
  
    // The main function that returns true if the graph is strongly 
    // connected, otherwise false 
    bool isSC(); 
  
    // Function that returns reverse (or transpose) of this graph 
    Graph getTranspose(); 
}; 
  
// A recursive function to print DFS starting from v 
void Graph::DFSUtil(int v, bool visited[]) 
{ 
    // Mark the current node as visited and print it 
    visited[v] = true; 
  
    // Recur for all the vertices adjacent to this vertex 
    list<int>::iterator i; 
    for (i = adj[v].begin(); i != adj[v].end(); ++i) 
        if (!visited[*i]) 
            DFSUtil(*i, visited); 
} 
  
// Function that returns reverse (or transpose) of this graph 
Graph Graph::getTranspose() 
{ 
    Graph g(V); 
    for (int v = 0; v < V; v++) 
    { 
        // Recur for all the vertices adjacent to this vertex 
        list<int>::iterator i; 
        for(i = adj[v].begin(); i != adj[v].end(); ++i) 
        { 
            g.adj[*i].push_back(v); 
        } 
    } 
    return g; 
} 
  
void Graph::addEdge(int v, int w) 
{ 
    adj[v].push_back(w); // Add w to v’s list. 
} 
  
// The main function that returns true if graph is strongly connected 
bool Graph::isSC() 
{ 
    // St1p 1: Mark all the vertices as not visited (For first DFS) 
    bool visited[V]; 
    for (int i = 0; i < V; i++) 
        visited[i] = false; 
  
    // Step 2: Do DFS traversal starting from first vertex. 
    DFSUtil(0, visited); 
  
     // If DFS traversal doesn’t visit all vertices, then return false. 
    for (int i = 0; i < V; i++) 
        if (visited[i] == false) 
             return false; 
  
    // Step 3: Create a reversed graph 
    Graph gr = getTranspose(); 
  
    // Step 4: Mark all the vertices as not visited (For second DFS) 
    for(int i = 0; i < V; i++) 
        visited[i] = false; 
  
    // Step 5: Do DFS for reversed graph starting from first vertex. 
    // Staring Vertex must be same starting point of first DFS 
    gr.DFSUtil(0, visited); 
  
    // If all vertices are not visited in second DFS, then 
    // return false 
    for (int i = 0; i < V; i++) 
        if (visited[i] == false) 
             return false; 
  
    return true; 
} 
  
// Driver program to test above functions 
int main() 
{ 
    // Create graphs given in the above diagrams 
    Graph g1(5); 
    g1.addEdge(0, 1); 
    g1.addEdge(1, 2); 
    g1.addEdge(2, 3); 
    g1.addEdge(3, 0); 
    g1.addEdge(2, 4); 
    g1.addEdge(4, 2); 
    g1.isSC()? cout << "Yes\n" : cout << "No\n"; 
  
    Graph g2(4); 
    g2.addEdge(0, 1); 
    g2.addEdge(1, 2); 
    g2.addEdge(2, 3); 
    g2.isSC()? cout << "Yes\n" : cout << "No\n"; 
  
    return 0; 
}

برنامه تشخیص گراف قویا همبند در جاوا

// Java program to check if a given directed graph is strongly 
// connected or not 
import java.io.*; 
import java.util.*; 
import java.util.LinkedList; 
  
// This class represents a directed graph using adjacency 
// list representation 
class Graph 
{ 
    private int V;   // No. of vertices 
    private LinkedList<Integer> adj[]; //Adjacency List 
  
    //Constructor 
    Graph(int v) 
    { 
        V = v; 
        adj = new LinkedList[v]; 
        for (int i=0; i<v; ++i) 
            adj[i] = new LinkedList(); 
    } 
  
    //Function to add an edge into the graph 
    void addEdge(int v,int w) {  adj[v].add(w); } 
  
    // A recursive function to print DFS starting from v 
    void DFSUtil(int v,Boolean visited[]) 
    { 
        // Mark the current node as visited and print it 
        visited[v] = true; 
  
        int n; 
  
        // Recur for all the vertices adjacent to this vertex 
        Iterator<Integer> i = adj[v].iterator(); 
        while (i.hasNext()) 
        { 
            n = i.next(); 
            if (!visited[n]) 
                DFSUtil(n,visited); 
        } 
    } 
  
    // Function that returns transpose of this graph 
    Graph getTranspose() 
    { 
        Graph g = new Graph(V); 
        for (int v = 0; v < V; v++) 
        { 
            // Recur for all the vertices adjacent to this vertex 
            Iterator<Integer> i = adj[v].listIterator(); 
            while (i.hasNext()) 
                g.adj[i.next()].add(v); 
        } 
        return g; 
    } 
  
    // The main function that returns true if graph is strongly 
    // connected 
    Boolean isSC() 
    { 
        // Step 1: Mark all the vertices as not visited 
        // (For first DFS) 
        Boolean visited[] = new Boolean[V]; 
        for (int i = 0; i < V; i++) 
            visited[i] = false; 
  
        // Step 2: Do DFS traversal starting from first vertex. 
        DFSUtil(0, visited); 
  
        // If DFS traversal doesn't visit all vertices, then 
        // return false. 
        for (int i = 0; i < V; i++) 
            if (visited[i] == false) 
                return false; 
  
        // Step 3: Create a reversed graph 
        Graph gr = getTranspose(); 
  
        // Step 4: Mark all the vertices as not visited (For 
        // second DFS) 
        for (int i = 0; i < V; i++) 
            visited[i] = false; 
  
        // Step 5: Do DFS for reversed graph starting from 
        // first vertex. Staring Vertex must be same starting 
        // point of first DFS 
        gr.DFSUtil(0, visited); 
  
        // If all vertices are not visited in second DFS, then 
        // return false 
        for (int i = 0; i < V; i++) 
            if (visited[i] == false) 
                return false; 
  
        return true; 
    } 
  
    public static void main(String args[]) 
    { 
        // Create graphs given in the above diagrams 
        Graph g1 = new Graph(5); 
        g1.addEdge(0, 1); 
        g1.addEdge(1, 2); 
        g1.addEdge(2, 3); 
        g1.addEdge(3, 0); 
        g1.addEdge(2, 4); 
        g1.addEdge(4, 2); 
        if (g1.isSC()) 
            System.out.println("Yes"); 
        else
            System.out.println("No"); 
  
        Graph g2 = new Graph(4); 
        g2.addEdge(0, 1); 
        g2.addEdge(1, 2); 
        g2.addEdge(2, 3); 
        if (g2.isSC()) 
            System.out.println("Yes"); 
        else
            System.out.println("No"); 
    } 
} 
// This code is contributed by Aakash Hasija 

برنامه تشخیص گراف قویا همبند در پایتون

# Python program to check if a given directed graph is strongly  
# connected or not 
  
from collections import defaultdict 
   
#This class represents a directed graph using adjacency list representation 
class Graph: 
   
    def __init__(self,vertices): 
        self.V= vertices #No. of vertices 
        self.graph = defaultdict(list) # default dictionary to store graph 
   
    # function to add an edge to graph 
    def addEdge(self,u,v): 
        self.graph[u].append(v) 
      
   
    #A function used by isSC() to perform DFS 
    def DFSUtil(self,v,visited): 
  
        # Mark the current node as visited  
        visited[v]= True
  
        #Recur for all the vertices adjacent to this vertex 
        for i in self.graph[v]: 
            if visited[i]==False: 
                self.DFSUtil(i,visited) 
  
  
    # Function that returns reverse (or transpose) of this graph 
    def getTranspose(self): 
  
        g = Graph(self.V) 
  
        # Recur for all the vertices adjacent to this vertex 
        for i in self.graph: 
            for j in self.graph[i]: 
                g.addEdge(j,i) 
          
        return g 
  
          
    # The main function that returns true if graph is strongly connected 
    def isSC(self): 
  
        # Step 1: Mark all the vertices as not visited (For first DFS) 
        visited =[False]*(self.V) 
          
        # Step 2: Do DFS traversal starting from first vertex. 
        self.DFSUtil(0,visited) 
  
        # If DFS traversal doesnt visit all vertices, then return false 
        if any(i == False for i in visited): 
            return False
  
        # Step 3: Create a reversed graph 
        gr = self.getTranspose() 
          
        # Step 4: Mark all the vertices as not visited (For second DFS) 
        visited =[False]*(self.V) 
  
        # Step 5: Do DFS for reversed graph starting from first vertex. 
        # Staring Vertex must be same starting point of first DFS 
        gr.DFSUtil(0,visited) 
  
        # If all vertices are not visited in second DFS, then 
        # return false 
        if any(i == False for i in visited): 
            return False
  
        return True
  
# Create a graph given in the above diagram 
g1 = Graph(5) 
g1.addEdge(0, 1) 
g1.addEdge(1, 2) 
g1.addEdge(2, 3) 
g1.addEdge(3, 0) 
g1.addEdge(2, 4) 
g1.addEdge(4, 2) 
print "Yes" if g1.isSC() else "No"
  
g2 = Graph(4) 
g2.addEdge(0, 1) 
g2.addEdge(1, 2) 
g2.addEdge(2, 3) 
print "Yes" if g2.isSC() else "No"
  
#This code is contributed by Neelam Yadav

خروجی قطعه کد بالا، به صورت زیر است.

Yes
No

پیچیدگی زمانی روش ارائه شده در بالا، برابر با «جستجوی اول عمق» است و اگر گراف با استفاده از ماتریس مجاورت ارائه شده باشد، از درجه (O(V+E خواهد بود. این رویکرد نیازمند دو بار پیمایش گراف است. می‌توان با استفاده از «الگوریتم تارژان مؤلفه‌های قویا هم‌بند» (Tarjan’s Strongly Connected Components Algorithm)، با یک بار پیمایش گراف این کار را انجام داد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده

^^