نظریه گراف (Graph Theory) در علوم کامپیوتر – به زبان ساده

اگر مشکلی برای حل کردن وجود نمیداشت؛ بسیاری از چیزهایی که در دنیا میبینیم به وجود نمیآمدند. این واقعیت در مورد همه چیز صدق میکند؛ اما در علوم رایانه امری کاملاً بدیهی است.
برای نمونه فردی نیاز داشته است تا ترتیب چیزهایی را حفظ کند و بدین ترتیب با ساختمانها داده مختلف کار کرده تا این که بهترین راهحل را برای یک مسئله که قصد حل کردنش را داشته پیدا کرده است. فرد دیگری نیازمند روش مناسبی برای ذخیرهسازی دادهها بوده است و از این رو با سیستمهای عددی مختلف کار کرده تا این که بهترین گزینه را برای نوع اطلاعاتی که میخواسته ذخیره کند یافته است. افراد مختلف نیازمند روش مناسبی برای وظایف برچسبگذاری و پردازش بودهاند و بنابراین بر مبنای ابزارهایی که داشتهاند، روشی برای گرد هم آوردن همه آنها به صورت یک سیستم منفرد که همه مقاصد را تأمین کند یافتهاند.
البته علوم رایانه تنها رشتهای نیست که بر مبنای یافتههای قبلی خود بنا شده و توسعه یافته است؛ اما شاید روش کار در این حوزه از یک نظر منحصر به فرد است، چون ابداعات علوم رایانه بر مبنای انتزاعهایی که از خود آن به دست میآید، صورت میگیرند.
انتزاعهایی که در علوم رایانه صورت میگیرد، بسیار حائز اهمیت هستند، زیرا در نهایت همه برنامهنویسان، تولیدکنندگان فناوری و همچنین مصرفکنندههای آن، از این انتزاع بهرهمند میشوند. در این نوشته به بررسی گرافها میپردازیم. بدین منظور باید کمی عمیقتر شویم و ابتدا ریشههای ژرفتر آن را در حوزهای از ریاضیات گسسته به نام نظریه گراف جستجو کنیم. اگر تا کنون با ریاضیات گسسته برخوردی نداشتهاید، جای نگرانی نیست؛ چون به کمک هم این بحث را به پیش میبریم و موانع را در این مسیر از پیش رو برمیداریم.
گرافها
زمانی که برای نخستین بار به ساختمانهای غیرخطی نگاه میکنیم، در مورد بنیادیترین خصوصیات آنها چیزهایی میآموزیم، مانند این که دادههایشان از ترتیب خاصی پیروی نمیکنند؛ یا دست کم ترتیبی عددی مشخصی ندارند. این حالت هنگام مشاهده آرایهها یا لیستهای پیوندی وجود دارد. درختها از یک گره ریشه آغاز میشوند و میتوانند به گرههای دیگر وصل شوند که به این معنی است که زیردرختهایی درون درخت وجود دارد. درختها با چند قاعده مشخص تعریف میشوند: گره ریشه منفرد میتواند به گرههای دیگر وصل باشد یا نباشد؛ اما در نهایت همه گرهها از یک ریشه مشتق میشوند. برخی درختها قواعد خاصتری دارند، مانند درختهای جستجوی دودویی که در هر زمان میتوانند تنها دو لینک به دو گره داشته باشند.
اما اگر این قواعد را کلاً کنار بگذاریم چطور؟ آنچه مشخص این است که این کار امکانپذیر است و در چنین صورتی دیگر با درخت سر و کار نداریم و با چیزی به نام گراف مواجه میشویم. درختها تنها نوع محدودی از گرافها هستند که قواعد خاصی در مورد آنها وجود دارد. هر درخت همواره یک گراف نیز محسوب میشود؛ اما همه گرافها درخت نیستند.
اینک سؤال این است که چه چیزی باعث میشود که درخت از بقیه گرافها متمایز باشد؟
تنها تفاوت در این است که درخت تنها یک جهت میتواند داشته باشد و این جهت از ریشه آغاز شده و به گرههای برگ یا گرههای فرزند حرکت میکند. درخت میتواند اتصالهای یکطرفهای نیز داشته باشد، یعنی یک گره فرزند میتواند تنها یک والد داشته باشد و یک درخت نمیتواند هیچ حلقه یا پیوند دوری داشته باشد.

در مورد گراف، همه این محدودیتها رفع میشوند. گرافها هیچ چیزی به مفهوم گره ریشه ندارند. گرهها میتوانند به هر روش دلخواهی به هم اتصال یابند. یک گره میتواند به پنج گره دیگر نیز اتصال داشته باشد. همچنین گرافها هیچ نماد گردش «یکطرفه» ندارند و به جای آن میتوانند جهتی برای آنها تعریف شده باشد و یا این که کلاً هیچ جهتی نداشته باشند. همچنین گرافها میتوانند برخی پیوندهای جهتدار و برخی پیوندهای غیر جهتدار داشته باشند. در آغاز توضیحات خود را از گرافهای ساده شروع میکنیم.
گرافهای جهتدار و گرافهای غیر جهتدار
اینک میدانیم که گرافها تقریباً همه قواعدی که در مورد درختها میدانیم را نقض میکنند. با این وجود، یک خصوصیت است که هر گراف باید داشته باشد و آن این است که هر گرافی همواره باید دست کم یک گره منفرد داشته باشد. همان طور که همه درختها به دست کم یک گره ریشه نیاز دارند تا آنها را به عنوان درخت در نظر بگریم، به طور مشابه هر گراف نیز باید دست کم یک گره منفرد داشته باشد تا بتوانیم آن را گراف بنامیم. یک گراف با تنها یک گره، معمولاً به نام یک گراف سینگلتون (singleton graph) نامیده میشود.
اغلب گرافهایی که با آنها سر و کار داریم اندکی پیچیدهتر هستند؛ اما جای نگرانی نیست چون قصد نداریم در این نوشته وارد بحث گرافهای خیلی پیچیده بشویم؛ گرچه برخی از گرافها واقعاً پیچیده هستند. در این بخش نگاهی به دو نوع از گراف خواهیم داشت که کاملاً آسان هستند و در مسائل مربوط به نظریه گراف کاملاً رایج هستند: گرافهای جهتدار و گرافهای غیر جهتدار. همان طور که میدانیم هیچ قاعده واقعی برای اتصال یک گره به گره دیگر در گراف وجود ندارد. یالها (که گاهی اوقات پیوند یا لینک نیز نامیده میشوند) میتوانند گرهها را به هر روش ممکن به هم متصل کنند.

انواع مختلف یالهای یک گراف زمانی که میخواهیم گرافهای مختلف را بازشناسی کرده و یا تعریف کنیم اهمیت مییابند. در واقع انواع یالهایی که یک گراف دارد، یکی از بزرگترین و بدیهیترین تفاوتهای بین یک گراف با گراف دیگر است. در اغلب موارد گرافها میتوانند دو نوع یال داشته باشند: یالی که جهتدار است و یالی که جهتی ندارد. این دو نوع یال را به ترتیب یال جهتدار و غیر جهتدار مینامیم.
در یک یال جهتدار، دو گره به روشی بسیار خاص به هم متصل میشوند. در مثال زیر، گره A به گره B وصل شده است. و تنها یک روش برای حرکت بین این دو گره وجود دارد، یعنی برای عبور تنها یک جهت وجود دارد. در اغلب موارد گره آغاز جهت را به نام مبدأ و گره انتهای یال را گره مقصد مینامند. در یک یال جهتدار تنها میتوان از گره مبدأ به مقصد حرکت کرد و پیمایش مسیر معکوس هرگز ممکن نیست.
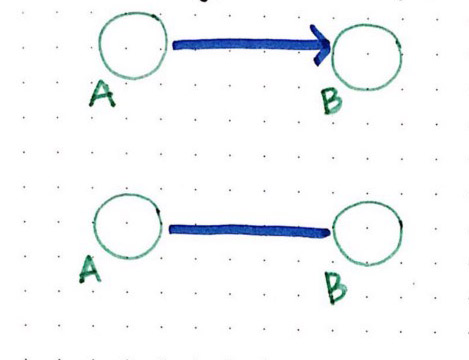
با این وجود، یالهای غیر جهتدار روش کاملاً متفاوتی دارند. در یک یال غیر جهتدار، مسیر بین دو گره دوطرفه است. یعنی مسیری که دو گره را به هم متصل میسازد از هر دو طرف قابل پیمایش است و گرههای مبدأ و مقصد به خط سیر ما بستگی دارند و ثابت نیستند.
تفاوت این دو در عمل کاملاً مهم است، چون یالها در یک گراف تعیین میکنند که گراف از چه نوع است. اگر همه یالها دریک گراف جهتدار باشند؛ گراف را یک گراف جهتدار (برخی اوقات digraph) مینامیم. اگر همه یالها در یک گراف غیر جهتدار باشند، این گراف را همان طور که احتمالاً حدس میزنید یک گراف غیر جهتدار مینامیم.
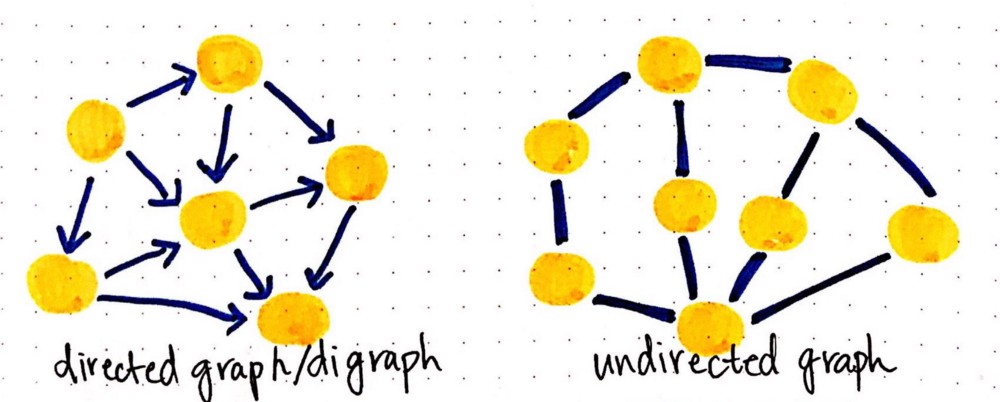
در ادامه منشأ همه این اصطلاحهای مربوط به گراف را بررسی میکنیم.
علوم رایانه مفاهیم زیادی را از رشتههای دیگر به خدمت گرفته است. به طور خاص بسیاری از مفاهیم از علوم منطق و ریاضیات وارد علوم رایانه شدهاند. گراف نیز از این قاعده مستثنی نیست.
ساختمان داده گراف آن چنان که در علوم رایانه میشناسیم از ریاضیات و شاخه مطالعه گراف که به نام نظریه گراف نیز نامیده میشود، وارد شده است. در ریاضیات، گرافها روشی برای بازنمایی رسمی یک شبکه هستند که اساساً مجموعهای از شیءهایی هستند که همه به یکدیگر وصل شدهاند.
زمانی که دانشمندان رایانه از نظریه گراف در کدهای خود استفاده کردند و در نهایت آن را به صورت یک ساختمان داده پیادهسازی کردند، چیزهای زیادی را تغییر ندادند. بنابراین اصطلاحهای زیادی که امروزه برای توصیف و پیادهسازی گرافها استفاده میکنیم، دقیقاً اصطلاحهایی هستند که ریاضیدانها برای اشاره به نظریه گراف مورد استفاده قرار میدهند.
برای نمونه بر اساس اصطلاحهای ریاضیاتی، گراف را به صورت زوجهای مرتب توصیف میکنیم. اگر از جبر دبیرستانی به خاطر داشته باشید، زوجهای مرتب را هنگام یادگیری مختصات زوج مرتب (x,y) یاد گرفتهایم. در این جا نیز مفهوم مشابهی استفاده میشود و تنها یک تفاوت وجود دارد و آن این است در گراف به جای x و y از v برای رأسها و از e برای یالها استفاده میشود.
تعریف رسمی ریاضیاتی یک گراف چنین است: (G = (V, E
لحظهای صبر کنید. چه میشود اگر گرافهای ما بیش از یک گره و بیش از یک یال داشته باشند. در واقع گرافها به طور کلی در صورتی که بیش از یک گره داشته باشند، معمولاً بیش از یک یال نیز دارند. تعریف چنین گرافهایی را در ادامه آوردهایم.
میدانیم که تعریف گراف به این دلیل صحیح است که زوج مرتب (V,E) اساساً از دو شیء تشکیل یافته است: مجموعهای از رئوس و مجموعهای از یالها.
استفاده از یک مثال همواره باعث تسهیل فرایند یادگیری میشود. بنابراین در ادامه مثالی برای یک گراف جهتدار با 8 رأس و 11 یال ارائه کردهایم.

در تعریف فوق زوج مرتب (V,E) را نوشتهایم؛ اما از آنجا که هر یک از این آیتمها یک شیء است، باید آنها را نیز بنویسیم. ما V را به صورت یک مجموعه نامرتب از ارجاعها به 8 رأس تعریف کردهایم. کلمه «نامرتب» در این جا کاملاً مهم است، زیرا همان طور که احتمالاً به یاد دارید، برخلاف درختها، در گراف هیچ سلسله مراتبی از گرهها وجود ندارد. یعنی لازم نیست آنها را به ترتیب لیست کنیم و از این لحاظ ترتیب اهمیتی ندارد.
همچنین باید E را به عنوان یک شیء تعریف کنیم که شامل دستهای از اشیای یال درون خود است. توجه کنید که اشیای یال ما نیز نامرتب هستند. از آنجا که مشغول تعریف یک گراف نامرتب هستیم، بنابراین هیچ معنی ثابتی برای گرافهای مبدأ و مقصد وجود نخواهد داشت. دقت کنید که این یک گراف غیر جهتدار است و این بدان معنی است که یالها دوطرفه هستند و گره مبدأ و گره مقصد ثابت نیستند. بنابراین هر یک از شیءهای یال ما نیز زوجهای نامرتب هستند.
اینک ممکن است کنجکاو شویم که پس تعریف گراف جهتدار گونه است؟ در مثال زیر نمونه دیگری ارائه شده است که شامل یک گراف جهتدار با سه رأس و سه یال است.

روش تعریف رأسها در این جا هیچ تفاوتی ندارد؛ اما با نگاهی دقیقتر به تعریف یالها میبینیم که شیءهای یال در این حالت زوجهای مرتب هستند، چون جهت در این مثال حائز اهمیت است. از آنجا که میتوان تنها از گره مبدأ به گره مقصد حرکت کرد، یالها باید مرتب باشند به طوری که گره مبدأ در تعریف هر یال، نخستین گره باشد.
اکنون با شیوه تعریف گرافها آشنا شدیم. در ادامه روش استفاده عملی از گرافها را بررسی میکنیم.
گرافهای کاملاً اجتماعی
گرافها همه جا در پیرامون ما حضور دارند؛ اما ممکن است در اکثر موارد نتوانیم آنها را ببینیم. در واقع شما با مطالعه همین نوشته نیز اکنون از یک گراف استفاده میکنید. وب خود یک ساختمان گراف بسیار عظیم است. زمانی که روی لینکها کلیک میکنیم و بین وبسایتهای مختلف حرکت میکنیم در واقع روی یک گراف در حال پیمایش هستیم. برخی اوقات این گرافها گرههایی دارند که یالهایشان غیر جهتدار است، یعنی میتوانیم از یک صفحه به صفحه دیگر رفته و به عقب بازگردیم. برخی اوقات نیز یالهای گراف ما جهتدار هستند، یعنی تنها از صفحه وب A میتوانیم به صفحه وب B برویم و نمیتوانیم به عقب بازگردیم.
اما مثال بهتری نیز برای گراف وجود دارد که تعاملهای روزانه ما با گرافها را به زیبایی نشان میدهد و آن شبکههای اجتماعی هستند.
فیسبوک به عنوان یک شبکه عظیم اجتماعی، نوعی گراف است. اگر در مورد کارکردهای این شبکه اجتماعی به دقت تأمل کنیم، بهتر میتوانیم شیوه تعریف آن را درک کنیم و بدانیم که چه نوع گرافی است. اگر روی فیسبوک فردی را به عنوان دوست اضافه کنیم، فرد دیگر نیز باید این درخواست را بپذیرد، چون در غیر این صورت رابطه دوستی شکل نمیگیرد. در این حالت رابطه دو نفر (معادل گره و یال در گراف) دوطرفه است. هیچ مفهومی به نام مبدأ و مقصد وجود ندارد، شما دوستی دارید و او نیز دوست شما است.
آیا میتوانید حدس بزنید فیسبوک چه نوع گرافی را پیادهسازی کرده است؟

روابط در فیسبوک دوطرفه هستند و اگر روابط دوستی را در فیسبوک به صورت یک گراف تعریف کنیم، یالهای آن همگی به صورت زوجهای نامرتب هستند. از سوی دیگر طرز کار توییتر کاملاً از فیسبوک متفاوت است. در توییتر فردی میتواند فرد دیگر را فالو کند؛ اما فرد دوم میتواند وی را فالو نکند.

توییتر را میتوان به صوت یک گراف جهتدار نمایش داد. هر یال که ایجاد میشود یک رابطه یکطرفه را نمایش میدهد. زمانی که شما فردی را در توییتر فالو میکنید، یک یال در گراف ایجاد میکنید که حساب کاربری شما به عنوان گره مبدأ و حساب کاربری فرد دیگر به عنوان گره مقصد محسوب میشود.
بنابراین زمانی که فرد دوم شما را فالو بک میکند چه رخ میدهد؟ آیا تغییری در یال شما ایجاد میشود؟ آیا این یال دوطرفه میشود؟ البته چنین نیست، چون شما میتوانید هر زمان فرد دوم را آنفالو کنید. زمانی که فرد دوم شما را فالو میکند، یک یال دوم از حساب کاربری وی به عنوان گره مبدأ به حساب کاربری شما به عنوان گره مقصد ایجاد میشود.
همین مدل در مورد وبسایت Medium نیز وجود دارد. شما در مدیوم میتوانید افراد دیگر را فالو یا آنفالو کنید. در واقع این مدل از شبکه همه جا حضور دارد. زمانی که لایههای فوقانی آن را جدا کنیم آنچه در عمل باقی میماند یک گراف است و گراف واقعاً ابزار قدرتمندی است.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای علوم کامپیوتر
- مجموعه آموزشهای برنامهنویسی
- آموزش نظریه گراف و کاربردها
- مجموعه آموزشهای ریاضیات
- آموزش درخت در نظریه گراف و کاربردها
- آموزش گراف در ساختمان گسسته
==












