چگالی سطحی بار الکتریکی چیست؟ – تعریف و توضیح + مثال

بر طبق فیزیک الکترومغناطیس، چگالی بار به صورت اندازه بار الکتریکی بر واحد حجم در فضا در یک، دو یا سه بعد، تعریف می‌شود. به عنوان مثال، چگالی سطحی بار یا حجمی به ترتیب برابر مقدار بار الکتریکی بر سطح یا حجم است. در این مطلب، در مورد چگالی سطحی بار و نحوه محاسبه آن بر روی سطوح مختلف صحبت می‌کنیم. در ادامه، چگالی بار خطی و حجمی را نیز به زبان ساده همراه با مثال‌های گوناگون، توضیح خواهیم داد.

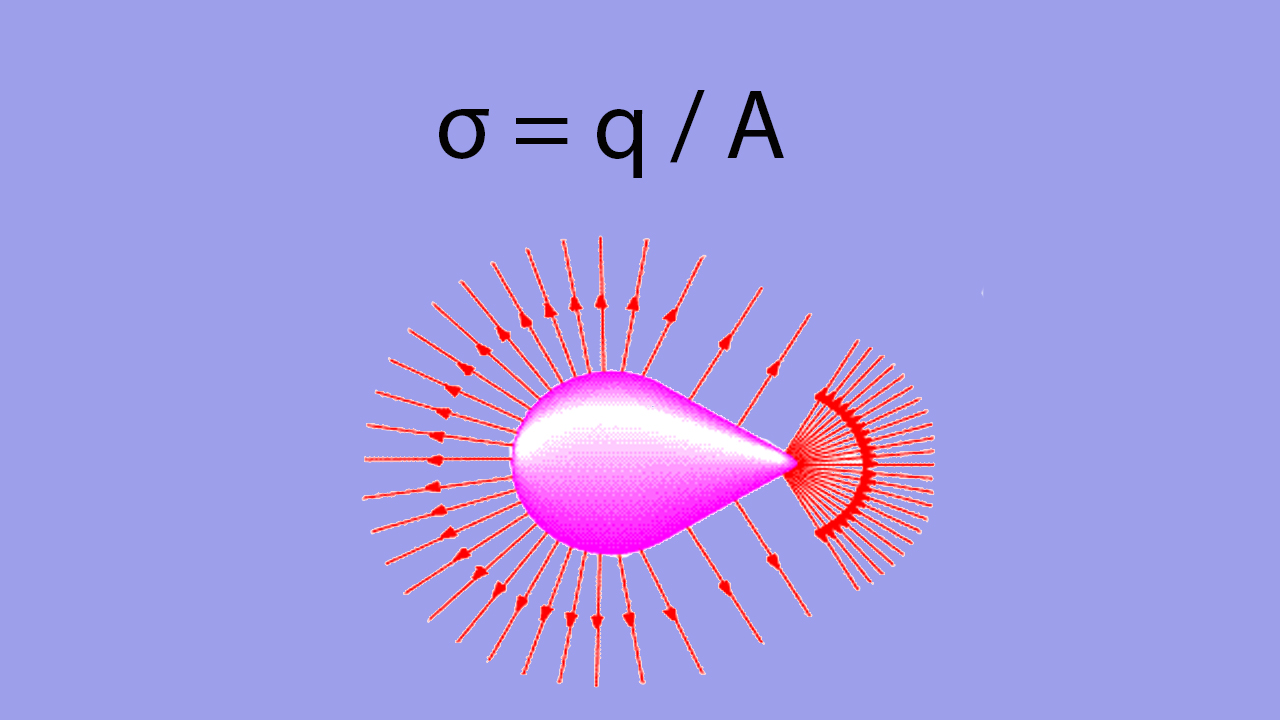
چگالی سطحی بار الکتریکی چیست ؟

در الکترومغناطیس، چگالی بار برابر بار الکتریکی بر واحد طول، مساحت یا حجم، است. چگالی سطحی بار ($$\sigma$$) به صورت مقدار بار الکتریکی بر واحد مساحت تعریف می‌شود.

چگالی سطحی بار الکتریکی را با دقت بیشتری بررسی و برای درک بهتر این مفهوم، ابتدا در مورد توزیع بار صحبت می‌کنیم. به مجموعه‌ای از بارهای الکتریکی، توزیع بار گفته می‌شود. توزیع بارهای الکتریکی به دو دسته کلی تقسیم می‌شود:

1. توزیع بار گسسته
2. توزیع بار پیوسته

به بارهای نقطه‌ای که در فاصله مشخصی از یکدیگر قرار گرفته‌اند، توزیع بار گسسته گفته می‌شود. بارهای گسسته قابل شمارش هستند. به عنوان مثال، یک بار نقطه‌ای ۵ نانوکولنی در نقطه یک و بار نقطه‌ای دیگری به بزرگی ۱۰ نانوکولن در نقطه ۲ و در فاصله ۱۰ سانتی‌متری از بار اول قرار گرفته است.

در توزیع بار پیوسته، بارهای الکتریکی به صورت نقطه‌ای و جدا از هم قرار نگرفته‌اند. به عنوان مثال، میله‌ای رسانا به طول یک متر را در نظر بگیرید. این میله را باردار می‌کنیم و بار آن مثبت می‌شود. بار مثبت به طور پیوسته در طول میله پخش شده است. در این حالت نمی‌توانیم بارها را به صورت جداگانه بشماریم. در واقع، در هر نقطه‌ای از میله بار داریم. توزیع بار پیوسته می‌تواند به دو صورت یکنواخت یا غیریکنواخت در میله پخش شود.

در توزیع بار یکنواخت، مقدار بارها در هر نقطه از میله با نقطه دیگر برابر است. در مقابل، در توزیع بار غیریکنواخت، مقدار بار در نقطه‌ای از میله کمتر یا بیشتر از مقدار بار در نقطه‌ای دیگر است. این قسمت را با ذکر مثالی ساده توضیح می‌دهیم. فرض کنید در صف نانوایی ایستاده‌اید. اگر فاصله افراد در صف از یکدیگر یکسان باشد، می‌گوییم افراد به صورت یکنواخت در صف قرار گرفته‌اند. اما اگر افراد بیشتری با فاصله کم در جلوی صف تجمع کرده باشند، صف غیریکنواخت خواهد بود. در نتیجه، در توزیع بار پیوسته کمیتی به نام چگالی بار را معرفی می‌کنیم. چگالی بار الکتریکی به سه دسته تقسیم می‌شود:

1. چگالی خطی بار
2. چگالی سطحی بار
3. چگالی حجمی بار

در این قسمت، در مورد چگالی سطحی بار الکتریکی توضیح می‌دهیم. در ادامه، در مورد چگالی‌ خطی و حجمی بار نیز صحبت خواهیم کرد.

در چگالی سطحی، بار بر روی سطح مشخصی به صورت پیوسته و یکنواخت یا پیوسته و غیریکنواخت، پخش شده است.

فرمول چگالی سطحی بار الکتریکی چیست ؟

چگالی سطحی بار برابر نسبت بار قرار گرفته بر روی سطح به مساحت آن سطح است و با استفاده از فرمول زیر محاسبه می‌شود:

$$\sigma = \frac{q}{A}$$

واحد چگالی سطحی بار برابر کولن بر متر مربع ($$\frac{C}{m^2}$$) است.

فرض کنید، بار الکتریکی به صورت یکنواخت بر روی صفحه‌ای رسانا پخش شده و $$\sigma = 10 \ \frac{C}{m^2}$$ است. معنای این جمله آن است که در مساحت یک متر مربع از صفحه، مقدار بار برابر ۱۰ کولن و در مساحت ۲۰ متر مربع از صفحه، مقدار بار الکتریکی برابر ۲۰ کولن خواهد بود.

دیمانسیون چگالی سطحی بار چیست ؟

بار الکتریکی برابر است با:

$$q = It$$

دیمانسیون بار الکتریکی برابر $$[IT]$$ و دیمانسیون مساحت برابر $$[L^2]$$ است. در نتیجه، دیمانسیون چگالی سطحی بار به صورت زیر نوشته خواهد شد:

$$[L^{-2} T I]$$

مثال اول محاسبه چگالی سطحی بار

چگالی سطحی بار رسانایی با بار ۵ کولن و مساحت ۱۰ متر مربع را به‌دست آورید.

پاسخ: بار رسانا و مساحت آن داده شده‌ است. چگالی سطحی بار با استفاده از فرمول زیر محاسبه می‌شود:

$$\sigma = \frac{q}{A}$$

با قرار دادن مقدار بار و مساحت در رابطه فوق داریم:

$$\sigma = \frac{q}{A} = \frac{5}{10} = 0.5 \ \frac{C}{m^2}$$

تاکنون با تعریف چگالی سطحی بار و فرمول محاسبه آن آشنا شدیم. در ادامه، نحوه محاسبه چگالی‌ سطحی بار شکل‌های مختلف را توضیح می‌دهیم. رساناها با شکل‌های متفاوت، مساحت‌های مختلفی دارند. بنابراین، مقدار چگالی سطحی بار آن‌ها متفاوت خواهد بود.

چگالی سطحی بار در کره رسانا

کره‌ای رسانا به شعاع r و بار کل Q بر روی سطح آن را در نظر بگیرید.

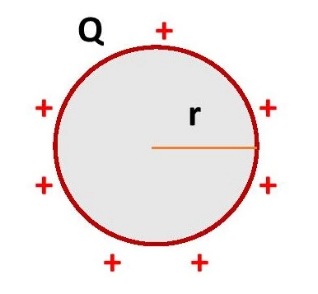
مساحت کره با استفاده از فرمول زیر به‌دست می‌آید:

$$A = 4 \pi r^2$$

بنابراین، چگالی سطحی بار آن به صورت زیر محاسبه خواهد شد:

$$\sigma = \frac{Q}{ 4 \pi r^2}$$

توجه به این نکته مهم است که چگالی سطحی بارِ پوسته کروی رسانا با مقدار آن در کره رسانایی با شعاع و بار یکسان، برابر خواهد بود. از آنجا که انحنای سطح کره در هر نقطه‌ای روی سطح یکسان است، چگالی سطحی بار در هر جایی بر روی سطح کره ثابت خواهد بود.

مثال محاسبه چگالی سطحی بار کره

چگالی سطحی بار کره‌ای به شعاع ۹ سانتی‌متر و مقدار بار ۱۲ کولن را به‌دست آورید.

پاسخ: چگالی سطحی بار با استفاده از رابطه زیر محاسبه می‌شود:

$$\sigma = \frac{q}{A}$$

مساحت کره به صورت زیر به‌دست می‌آید:

$$A = 4 \pi r^2 \\ A = 4 \pi (0.09)^ 2 \\ A = 0.1017 \ m^2$$

با قرار دادن مساحت کره در رابطه چگالی سطحی، داریم:

 $$\sigma = \frac{12}{0.1017 } = 117.994 \ \frac{C}{m^2}$$

چگالی سطحی بار در استوانه رسانا

استوانه‌ای به طول L و شعاع r در نظر بگیرید. همان‌طور که در تصویر زیر مشاهده می‌شود، استوانه سه سطح دارد:

• دو سطح تخت در بالا و پایین
• سطح منحنی

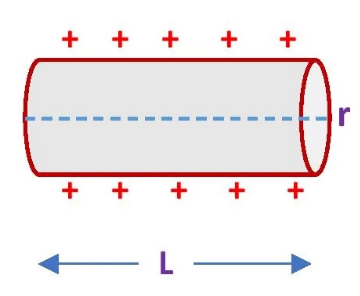
چگالی بار هر یک از این سطوح متفاوت از دیگری خواهد بود. مساحت سطح منحنی برابر $$2 \pi r L$$ و مساحت هر یک از سطوح تخت برابر $$\pi r^2$$ است. بنابراین، فرمول چگالی سطحی بارِ سطح منحنی استوانه عبارت است از:

$$\sigma = \frac{Q}{ 2 \pi r L}$$

همچنین، چگالی سطحیِ سطح تخت برابر است با:

$$\sigma = \frac{Q}{\pi r ^ 2}$$

در رابطه‌های بالا، Q مقدار بار روی سطح استوانه است. چگالی سطحی بار استوانه با استفاده از این دو رابطه به‌دست خواهد آمد.

چگالی سطحی بار الکتریکی در خازن

فرمول محاسبه چگالی سطحی بار خازن به شکل و مساحت صفحات آن بستگی دارد. اگر خازن از دو صفحه مستطیل شکل به طول L و عرض b تشکیل شده باشد، مساحت هر صفحه برابر $$A = L b$$ است. در نتیجه، چگالی سطحی بار آن با استفاده از فرمول $$\sigma = \frac {Q} {L b}$$ محاسبه می‌شود.

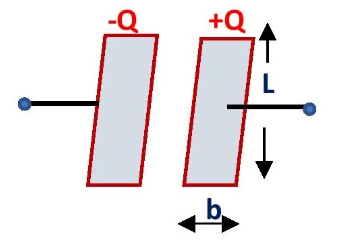
اگر صفحات تشکیل‌دهنده خازن، دایره‌ای به شعاع r باشند، چگالی سطحی بار با استفاده از رابطه زیر به‌دست خواهد آمد:

$$\sigma = \frac{Q} {\pi r ^ 2}$$

چگالی سطحی بار در رسانایی با شکل نامنظم چگونه است؟

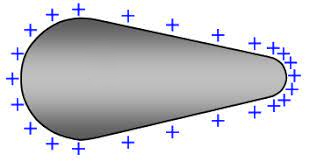
در رسانایی با شکل نامنظم، مساحت در نقاط مختلف سطح، متفاوت خواهد بود. از این رو، مقدار چگالی سطحی بار از نقطه‌ای به نقطه دیگر تغییر می‌کند. مقدار این کمیت در ناحیه‌ای با انحنای بیشتر، بزرگ‌تر است. این بدان معنا است که مقدار چگالی سطحی بار در لبه‌ها بیشتر خواهد بود. بنابراین، فرمول مشخصی برای محاسبه چگالی سطحی برای رسانایی با شکل نامشخص وجود ندارد.

چگالی سطحی بار به مقدار انحنای رسانا بستگی دارد. هرچه انحنا بیشتر باشد، چگالی سطحی نیز بزرگ‌تر خواهد بود. به عنوان مثال، کره‌ای به شعاع r را در نظر بگیرید. همان‌طور که گفتیم چگالی سطحی بار این کره با استفاده از فرمول $$\sigma = \frac {Q} {4 \pi r^2}$$ به‌دست می‌آید. در کره، انحنای بزرگ‌تر به معنای شعاع کوچک‌تر است. همان‌گونه که در رابطه چگالی سطحی دیده می‌شود، مقدار این کمیت با مجذور شعاع کره نسبت عکس دارد. در نتیجه، هر چه شعاع کوچک‌تر باشد، چگالی سطحی کره بزرگ‌تر خواهد بود.

نکته: چگالی سطحی بار با افزایش انحنای سطح رسانا، افزایش می‌یابد.

مثال چگالی سطحی بار رسانایی با شکل نامنظم

چگالی سطحی بار رسانایی با شکل نامنظم برابر است با:

1. صفر
2. بی‌نهایت
3. ثابت
4. در نقطه‌های مختلف، متفاوت است.

پاسخ: چگالی سطحی بار در رسانایی با شکل نامنظم در نقاطی با شعاع انحنای کوچک‌تر، بزرگ‌تر خواهد بود. به بیان دیگر، چگالی سطحی متناسب با معکوس شعاع انحنا است. از آنجا که شعاع انحنا در نقاط تیز، کمینه و در نقاط تخت، بیشینه است، مقدار چگالی سطحی در نقاط تیز زیاد و در نقاط تخت، کم خواهد بود.

برای درک بهتر این قسمت، انحنا یا خمیدگی را به اختصار توضیح می‌دهیم.

انحنا چیست ؟

صفحه‌ای با انحنای مشخص به شکل $$y = f(x)$$ در نظر بگیرید. فرض کنید خط مماس در نقطه $$M (x,y)$$ بر این منحنی رسم شده است. زاویه خط مماس با محور افقی برابر $$\alpha$$ است.

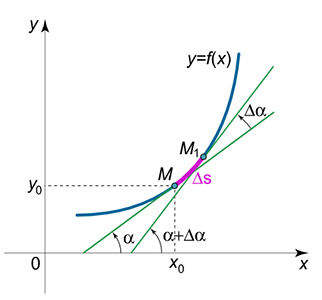
در حرکت از نقطه $$M$$ به نقطه $$M_1$$، جابجایی به اندازه $$\triangle s$$ بر روی قوس منحنی انجام شده است. مکان خط مماس و زاویه آن با محور $$x$$ ($$\alpha + \triangle x)$$ در این جابجایی نیز تغییر کرده است. بنابراین، با جابجایی نقطه به اندازه $$\triangle s$$ بر روی منحنی، خط مماس به اندازه زاویه $$\triangle \alpha$$ می‌چرخد. به نسبت $$\frac {\triangle \alpha} {\triangle s}$$ خمیدگی میانگین قوس $$MM_1$$ گفته می‌شود. با کوچک شدن جابجایی و میل کردن آن به سمت صفر، انحنای منحنی در نقطه $$M$$ به صورت زیر به‌دست می‌آید:

$$K = \lim_{\triangle s \rightarrow 0} |\frac{\triangle \alpha}{\triangle s}|$$

به بیان دیگر، انحنای در نقطه‌ای از منحنی برابر سرعت چرخش خط مماس بر منحنی در آن نقطه است.

برای منحنی با فرمول $$y = f(x)$$، انحنا در نقطه $$M(x,y)$$ به صورت زیر تعریف می‌شود:

$$K = \frac{|y'' (x)|}{[1 + (y'(x))^2]^{\frac{3}{2}}}$$

اگر منحنی به صورت پارامتری و توسط معادلات $$x = x(t)$$ و $$y = y(t)$$ تعریف شده باشد، انحنا در نقطه $$M(x,y)$$ با استفاده از رابطه زیر محاسبه می‌شود:

$$K = \frac{|x' y '' - y' x '' |}{[(x')^2 + (y')^2]^{\frac{3}{2}}}$$

همچنین، اگر رابطه منحنی به صورت معادله قطبی $$r = r (\theta)$$ نوشته شده باشد، انحنا با استفاده از فرمول زیر محاسبه خواهد شد:

$$K = \frac{|r^2 + 2 (r')^2 - r r'' |}{[r^2 + (r')^2]^{\frac{3}{2}}}$$

شعاع انحنای منحنی در نقطه $$M(x,y)$$ متناسب با معکوس انحنای منحنی در این نقطه است:

$$R = \frac{1} {K}$$

مثال محاسبه انحنای بیضی در راس

انحنای بیضی با معادله $$\frac{x^2}{a^2} + \frac{y^2}{b^2} =1$$ را در راس‌های آن به‌دست آورید.

پاسخ: برای حل این مثال کافی است که انحنای بیضی را در دو نقطه $$A(a,0)$$ و $$B(0,b)$$ به‌دست آوریم، زیرا به دلیل تقارن منحنی، انحنای دو راس مقابل با یکدیگر برابر است.

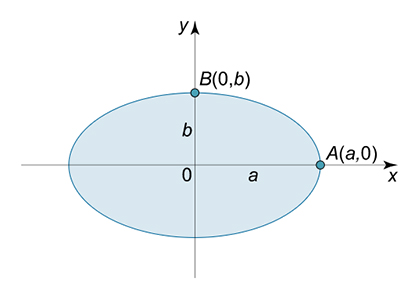
برای محاسبه انحنای بیضی، بهتر است معادله کانونی آن را به شکل معادله پارامتری بنویسیم:

$$x = a \cos t, \ \ \ y = b \sin t$$

t پارامتر است. مقدار آن در نقطه $$A(a,0)$$ برابر صفر و در نقطه $$B(0,b)$$ برابر $$\frac {\pi} {2}$$ fi به‌دست می‌آید. مشتق‌های اول و دوم $$x$$ و $$y$$ را حساب می‌کنیم:

$$x' = x'_t = (a \cos t)' = - \ a \sin t, \ \ \ x'' = x_{tt}'' = ( - \ a \sin t)' = - \ a \cos t \\ y' = y_t' = (b \sin t)' = a \cos t , \ \ \ y '' = y ''_{tt} = (b \cos t) ' = - \ \sin t$$

انحنای نمودار پارامتری با استفاده از فرمول زیر به‌دست می‌آید:

$$K = \frac{|x' y '' - y' x '' |}{[(x')^2 + (y')^2]^{\frac{3}{2}}}$$

با جایگذاری مشتق‌های به‌دست آمده در رابطه فوق، داریم:

$$K = \frac{|ab \sin^2 t + ab \cos^2 t|}{(a^2 \sin^2 t+ b^2 \cos ^2 t)^ {\frac{3}{2}}} = \frac{| ab \ (\sin ^2t + \cos^2 t)|}{(a^2 \sin^2 t+ b^2 \cos ^2 t)^ {\frac{3}{2}}} = \frac{ab}{{(a^2 \sin^2 t+ b^2 \cos ^2 t)^ {\frac{3}{2}}}}$$

در ادامه، مقدار انحنا در دو راس $$A(a,0)$$ و $$B(0,b)$$ را به‌دست می‌آوریم:

$$K (A) = K (t= 0) = \frac{ab}{{(a^2 \sin^2 0+ b^2 \cos ^2 0)^ {\frac{3}{2}}}} = \frac{ab}{(b^2)^{\frac{3}{2}}} = \frac{ab}{b^3}= \frac{a}{b^2} \\ K (B) = K (t= \frac{\pi}{2}) = \frac{ab}{{(a^2 \sin^2 \frac{\pi}{2}+ b^2 \cos ^2 \frac{\pi}{2})^ {\frac{3}{2}}}} = \frac{ab}{(a^2)^{\frac{3}{2}}} = \frac{ab}{a^3}= \frac{b}{a^2}$$

مثال محاسبه انحنا شعاع انحنای سهمی در مبدا مختصات و نقطه دلخواه

انحنا و شعاع انحنای سهمی به معادله $$y = x^2$$ را در مبدا مختصات و نقطه‌ای دلخواه به‌دست آورید و مقدار آن‌ها را با یکدیگر مقایسه کنید.

پاسخ: مشتق تابع داده شده را محاسبه می‌کنیم:

$$y' = (x^2) ' = 2 x; \ \ \ y '' = (2x) ' = 2$$

$$K = \frac{y '' }{[1 + (y ')^2]^{\frac{3}{2}} } = \frac{2 }{[1 + (2x)^2]^{\frac{3}{2}} } = \frac{2}{(1 + 4x^2)^\frac{3}{2}}$$

در مبدا مختصات ($$x =0$$)، انحنا و شعاع انحنای نمودار به صورت زیر محاسبه می‌شوند:

$$K (x =0) = \frac{2}{(1 + 4 (0)^2)^{\frac{3}{2}}} = 2, \ \ \ R = \frac{1}{K} = \frac{1}{2}$$

در ادامه مثال خواسته شده است که این دو مقدار در نقطه دلخواه دیگری محاسبه و با مقدار آن‌ها در مبدا مختصات مقایسه شوند. برای این کار نقطه $$(1,1)$$ در نظر می‌گیریم:

$$K (x =1) = \frac{2}{(1 + 4 (1)^2)^{\frac{3}{2}}} = 0.17, \ \ \ R = \frac{1}{K} = \frac{1}{0.17}= 5.6$$

همان‌طور که مشاهده می‌شود در نقطه $$(1,1)$$ شعاع انحنا بزرگ‌تر و مقدار انحنا کمتر است. در نتیجه، اگر سهمی را رسانایی فلزی در نظر بگیریم، چگالی سطحی بار در نوک آن یعنی نقطه $$(0,0)$$ بزرگ‌تر از نقطه $$(1,1)$$ است.

نحوه محاسبه چگالی سطحی بار

برای به‌دست آوردن مقدار کمیتی فیزیکی، باید از فرمول مرتبط با آن کمیت استفاده کنید. در مطالب بالا، فرمول محاسبه چگالی سطحی برخی اشکال هندسی را بیان کردیم. در واقع، برای محاسبه چگالی سطحی بار به دو کمیت نیاز داریم:

1. مقدار کل بار بر روی سطح رسانا
2. مساحت کل رسانا

مثال محاسبه بار بر روی کره رسانا

چگالی سطحی بار کره‌ای رسانا به شعاع ۱۰ سانتی‌متر برابر $$0.7 \ \frac{C} {m^2}$$ است. مقدار بار کل بر روی سطح آن را به‌دست آورید.

پاسخ: چگالی سطحی بار کره برابر $$0.7 \ \frac{C} {m^2}$$ و شعاع آن برابر ۱۰ سانتی‌متر یا ۰/۱ متر است. بنابراین، مساحت کره برابر است با:

$$A = 4 \pi r^2 = 4 \times(3.14) \times (0.1)^2 = 0.1256 \ m^2$$

بار کل بر روی سطح کره با استفاده از رابطه زیر به‌دست می‌آید:

$$Q = \sigma A \\ Q = 0.7 \times 0.1256 = 0.8792 \ C$$

تاکنون با چگالی بار در دو بعد، یعنی چگالی سطحی بار آشنا شدیم و روش محاسبه آن را توضیح دادیم. در ادامه، در مورد چگالی بار در یک و دو بعد یعنی چگالی خطی و چگالی حجمی بار صحبت خواهیم کرد.

چگالی خطی بار

به توزیع بار الکتریکی در امتداد طولی رسانا، توزیع بار خطی می‌گوییم. به مقدار بار الکتریکی توزیع شده در واحد طول رسانا، توزیع خطی بار گفته و با $$\lambda$$ نشان داده می‌شود.

فرمول چگالی خطی بار

اگر طول رسانایی برابر $$L$$ و بار کل آن برابر $$Q$$ باشد، چگالی خطی آن با استفاده از فرمول زیر محاسبه می‌شود:

$$\lambda = \frac{Q}{L}$$

رابطه فوق کلی‌ترین فرمول محاسبه چگالی خطی بار است و برای هر رسانای خطی به کار برده می‌شود.

واحد چگالی خطی بار

واحد SI چگالی خطی بار برابر کولن بر متر ($$\frac{C} {m}$$) است.

دیمانسیون چگالی خطی بار

دیمانسیون بار الکتریکی برابر $$[TI]$$ و طول برابر $$[L]$$ است. بنابراین، فرمول دیمانسیونی چگالی خطی بار برابر $$[ L^{-1} TI]$$ خواهد بود.

رابطه انتگرالی بین بار کل و چگالی خطی بار

رسانایی به طول $$L$$ و چگالی خطی بار $$\lambda$$ در نظر بگیرید. مقدار بار در طول بسیار کوچک $$dl$$ برابر است با:

$$d Q = \lambda . dl$$

مقدار کل بار رسانا به صورت زیر به‌دست می‌آید:

$$Q = \int \lambda . dl$$

رابطه فوق می‌تواند برای هر توزیع خطی بار استفاده شود.

نحوه محاسبه توزیع خطی بار

محاسبه چگالی خطی بار رسانا بسیار آسان است. برای محاسبه آن، دانستن مقدار بار بر روی رسانا و طول آن کافی است. با دانستن این دو مقدار و قرار دادن آن در فرمول مناسب، چگالی خطی به‌دست می‌آید.

محاسبه چگالی خطی بار استوانه

استوانه‌ای به طول ۱۵ سانتی‌متر و بار کل ۲ کولن را در نظر بگیرید. چگالی خطی بار با استفاده از فرمول زیر محاسبه می‌شود:

 $$\lambda = \frac{Q}{L}$$

با قرار دادن بار کل و طول استوانه در رابطه فوق داریم:

$$\lambda = \frac{2}{0.15}= 13.33 \ \frac {C}{m}$$

چگالی حجمی بار

بارهای الکتریکی در رسانای سه‌بعدی می‌توانند داخل حجم آن قرار داشته باشند. به توزیع بار الکتریکی داخل حجم رسانا، مانند کره و استوانه، توزیع بار حجمی گفته می‌شود. چگالی حجمی بار رسانا به صورت مقدار بار ذخیره شده در واحد حجم رسانا، تعریف و با $$\rho$$ نشان داده می‌شود.

فرمول چگالی حجمی بار

اگر $$Q$$ مقدار بار الکتریکی داخل حجم $$V$$ باشد، چگالی حجمی بار با استفاده از رابطه زیر به دست می‌آید:

$$\rho = \frac{Q}{V}$$

از آنجا که حجم شکل‌های مختلف از رابطه‌های مختلفی به‌دست می‌آید، فرمول چگالی حجمی از رسانایی به رسانای دیگر متفاوت خواهد بود.

واحد چگالی حجمی بار

واحد SI بار الکتریکی کولن ($$C$$) و حجم مترمکعب ($$m^3$$) است. بنابراین، واحد SI چگالی حجمی بار برابر $$\frac {C} {m^3}$$ خواهد بود.

دیمانسیون چگالی حجمی بار

دیمانسیون بار الکتریکی برابر $$[TI]$$ و حجم برابر $$[L^3]$$ است. بنابراین، فرمول دیمانسیونی چگالی خطی بار برابر $$[ L^{3} TI]$$ خواهد بود.

چگالی حجمی بار کره

کره‌ای به شعاع $$R$$ و مقدار بار کل $$Q$$ داخل حجم آن در نظر بگیرید.

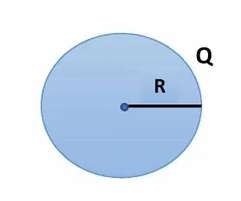
برای محاسبه چگالی حجمی کره، ابتدا حجم آن را به‌دست می‌آوریم:

$$V = \frac{4}{3} \pi r^3$$

با قرار دادن حجم کره در رابطه $$\rho = \frac{Q}{V}$$، چگالی حجمی آن به صورت زیر محاسبه خواهد شد:

$$\rho = \frac{Q}{\frac{4}{3} \pi r^3}$$

چگالی حجمی بار استوانه

استوانه‌ای به طول $$L$$ و شعاع $$r$$ در نظر بگیرید. اگر بار کلِ حجم استوانه برابر $$Q$$ باشد، چگالی حجمی آن به صورت زیر به‌دست می‌آید:

$$\rho = \frac{Q}{\pi r^2 L}$$

رابطه انتگرالی بین بار کل و چگالی حجمی بار

رسانایی به حجم $$V$$ و چگالی حجمی $$\rho$$ در نظر بگیرید که بار کل پخش شده در حجم آن برابر $$Q$$ است. اگر حجم بسیار کوچکی از حجم کلی را در نظر بگیریم، بار آن برابر است با:

$$dQ = \rho dV$$

در نتیجه، بار کل برابر است با:

$$Q = \int \rho . dV$$

تاکنون، با چگالی خطی، سطحی و حجمی بار الکتریکی و نحوه محاسبه آن‌ها آشنا شدیم. اما سوالی که ممکن است برای شما مطرح شود آن است که از این چگالی‌های بار چه استفاده‌ای می‌‌توان کرد. پاسخ به این پرسش بسیار واضح است، از آن‌ها برای محاسبه میدان و پتانسیل الکتریکی رساناهای مختلف استفاده می‌شود.

محاسبه میدان الکتریکی توزیع بارهای مختلف

گفتیم توزیع بار الکتریکی به دو دسته پیوسته و گسسته، تقسیم می‌شود. اگر توزیع بار گسسته باشد، میدان و پتانسیل الکتریکی با استفاده از رابطه‌های زیر به آسانی محاسبه می‌شوند:

$$E = \frac{1}{4 \pi \epsilon_0}\frac{q}{r^2 }\\ V = \frac{1}{4 \pi \epsilon_0}\frac{q}{r }$$

برای محاسبه میدان در توزیع بار پیوسته، آن را بخش‌های بسیار کوچکی تقسیم و با هر بخش کوچک همانند بار نقطه‌ای رفتار می‌کنیم.

نخستین گام تعریف چگالی بار برای توزیع بار در امتداد خط، بر روی سطح یا داخل حجم است.

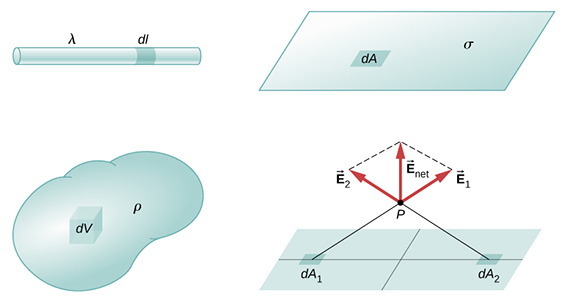
مقدار بار در قسمت بسیار کوچکی از توزیع بار پیوسته در یک، دو یا سه بعد به صورت زیر به‌دست می‌آید:

$$dq = \lambda dl \\ dq = \sigma dA \\ dq = \rho dV$$

میدان الکتریکی حاصل از چند بار الکتریکی نقطه‌ای در نقطه P، برابر است با:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \sum_{ i =1}^N (\frac{q_i}{r^2})\overrightarrow{r}$$

به هنگام محاسبه میدان الکتریکی ناشی از توزیع بار پیوسته، جمع به انتگرال تبدیل می‌شود:

• میدان الکتریکی ناشی از چگالی خطی بار

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{line} (\frac{\lambda dl}{r^2})\overrightarrow{r}$$

• میدان الکتریکی ناشی از چگالی سطحی بار

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{surface} (\frac{\sigma dA}{r^2})\overrightarrow{r}$$

• میدان الکتریکی ناشی از چگالی حجمی بار

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{volume} (\frac{\rho dV}{r^2})\overrightarrow{r}$$

در معادله‌های بالا به معنای $$r$$ در مخرج کسر، دقت کنید. $$r$$ فاصله بین نقطه P و بار خطی، سطحی یا حجمی بسیار کوچک است. همچنین، $$\overrightarrow{r}$$ جهت میدان الکتریکی را نشان می‌دهد.

مثال محاسبه میدان الکتریکی میله رسانا

میدان الکتریکی را در نقطه P به فاصله z از میله‌ای رسانا به طول L و چگالی خطی بار یکنواخت $$\lambda$$ به‌دست آورید. فرض کنید نقطه P بر روی عمود منصف میله قرار گرفته است.

پاسخ: از آنجا که توزیع بار میله پیوسته است، آن را به بخش‌های بسیار کوچکی به طول $$dl$$ تقسیم می‌کنیم. بار هر قسمت کوچک برابر است با:

$$dq = \lambda dl$$

برای به‌دست آوردن میدان الکتریکی به تصویر زیر توجه کنید. عمود منصف میله را رسم و دو قسمت بسیار کوچک از آن را به فاصله مساوی از عمود منصف انتخاب می‌کنیم و میدان الکتریکی حاصل از این دو قسمت را در نقطه P به‌دست می‌آوریم.

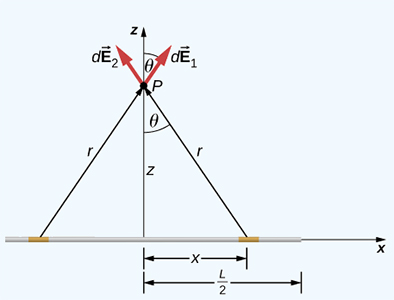
همان‌طور که در تصویر دیده می‌شود، میدان‌های الکتریکی جزئی در راستای محور x یکدیگر را خنثی و در راستای محور z، با یکدیگر جمع می‌شوند. با انتگرال‌گیری میدان الکتریکی جزئی بر روی سیم، میدان الکتریکی کل را به‌دست می‌آوریم.

میدان الکتریکی برای بار خطی با استفاده از رابطه زیر محاسبه می‌شود:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{line} (\frac{\lambda dl}{r^2})\overrightarrow{r}$$

میدان الکتریکی کل، $$\overrightarrow{E}(P)$$، برابر جمع برداری میدان‌های حاصل از بارهای جزئی در هر طرف میله است:

$$\overrightarrow{E}(P) = \overrightarrow{E_1} + \overrightarrow{E_2} \\ = E_ {1x} \overrightarrow{i} + E_ {1z} \overrightarrow{k}+ E_ {2x} (\overrightarrow{-i}) + E_ {2z} \overrightarrow{k}$$

از آنجا که هر دو بار جزئی قرار گرفته بر روی میله با یکدیگر مساوی هستند و در فاصله یکسان از نقطه P قرار گرفته‌اند، دو میدان $$E_{1x}$$ و $$E_{2x}$$ با یکدیگر برابر خواهند بود. بنابراین، یکدیگر را خنثی می‌کنند:

$$\overrightarrow{E}(P) = E_ {1z} \overrightarrow{k}+ E_ {2z} \overrightarrow{k} \\ = E_1 \cos \theta \ \overrightarrow{k} + E_2 \cos \theta \ \overrightarrow{k}$$

با توجه به تقارن شکل، این دو مولفه نیز با یکدیگر برابر هستند، بنابراین داریم:

$$\overrightarrow{E}(P) = \frac{1}{4 \pi \epsilon_0} \int \frac{\lambda dl}{r^2} \cos \theta \ \overrightarrow{k } + \frac{1}{4 \pi \epsilon_0} \int \frac{\lambda dl}{r^2} \cos \theta \ \overrightarrow{k } \\ = \frac{1}{4 \pi \epsilon_0} \int_{0}^{\frac{L}{2}} \frac{2 \lambda dx}{r^2}\cos \theta \ \overrightarrow{k}$$

$$dl$$ برابر $$dx$$ است، زیرا انتگرال‌گیری در امتداد محور x انجام می‌شود. برای محاسبه انتگرال، $$r$$ و $$\cos \theta$$ را بر حسب مقدارهای داده شده و $$x$$ می‌نویسیم:

$$r = (z^2 + x^2 ) ^ {\frac{1}{2}} \\ \cos \theta = \frac{z}{r} = \frac{z}{(z^2 + x^2 ) ^ {\frac{1}{2}}}$$

با جایگزین کردن عبارت‌های بالا در انتگرال، داریم:

$$\overrightarrow{E (P)} = \frac{1}{4 \pi \epsilon_0}\int_{0 }^{\frac{L}{2}} \frac{2 \lambda dx}{(z^2 + x^2 ) } \frac{z}{(z^2 + x^2 ) ^ {\frac{1}{2}} } \overrightarrow{k} \\ = \frac{1}{4 \pi \epsilon_0}\int_{0 }^{\frac{L}{2}} \frac{2 \lambda z}{(z^2 + x^2 )^ {\frac{3}{2}} } dx \overrightarrow{k} \\ = \frac{2 \lambda z}{4 \pi \epsilon _0} [ \frac{x}{z^2 \sqrt{z^2 + x^2}}]_0^{\frac{L}{2}} \ \overrightarrow{k}$$

در نتیجه، میدان الکتریکی حاصل از میله با بار خطی یکنواخت برابر است با:

$$\overrightarrow{E} (z) = \frac{1}{4 \pi \epsilon_0}\frac{\lambda L}{z \sqrt{z^2 + \frac{L^2}{4}}} \ \overrightarrow{k}$$

اگر طول میله نامحدود باشد، میدان الکتریکی چه مقدار خواهد بود؟

در این حالت نیز مانند حالت قبل، مولفه‌های افقی میدان یکدیگر را خنثی می‌کنند، بنابراین میدان جهت میدان الکتریکی کل، تنها در راستای محور z است:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{ - \infty}^{\infty} \frac{\lambda dx}{r^2} \ \cos \theta \ \overrightarrow{k}$$

مانند حالت میله محدود،‌ $$r$$ و $$\cos \theta$$ را بر حسب مقدارهای داده شده و $$x$$ می‌نویسیم:

$$r = (z^2 + x^2 ) ^ {\frac{1}{2}} \\ \cos \theta = \frac{z}{r} = \frac{z}{(z^2 + x^2 ) ^ {\frac{1}{2}}}$$

با جایگذاری عبارت‌های فوق در انتگرال، میدان الکتریکی میله نامحدود به صورت زیر به‌دست می‌آید:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0}\int_{- \infty}^{\infty} \frac{\lambda dx }{(z^2 + x^2) } \frac{z}{(z^2 + x^2)^ {\frac{1}{2}}} \ \overrightarrow{k} \\ = \frac{1}{4 \pi \epsilon_0}\int_{- \infty}^{\infty} \frac{\lambda z }{(z^2 + x^2)^{\frac{3}{2} }} \ dx \ \overrightarrow{k} \\ = \frac{1}{4 \pi \epsilon_0} [ \frac{x}{z^2 \sqrt{z^2 + x^2}}] _{- \ \infty} ^ {\infty} \ \overrightarrow{k } \\ \overrightarrow{E} (z) = \frac{1}{4 \pi \epsilon_0}\frac{2 \lambda}{z} \ \overrightarrow{k}$$

مثال محاسبه میدان الکتریکی حلقه رسانا

حلقه‌ای با بار خطی یکنواخت $$\lambda$$ و شعاع R در نظر بگیرید. میدان الکتریکی حاصل از این حلقه را در نقطه P واقع بر خط گذرنده از مرکز حلقه، به‌دست آورید.

پاسخ: در این حالت، بار بر روی دایره توزیع شده است. حلقه را به بخش‌های بسیار کوچکی به شکل کمان تقسیم و برای محاسبه میدان از مختصات قطبی استفاده می‌کنیم.

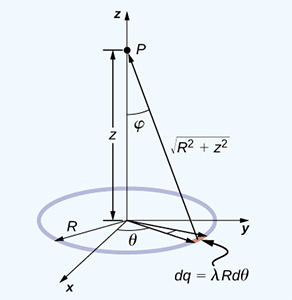
میدان الکتریکی حاصل از بار نقطه خطی با استفاده از فرمول زیر به‌دست می‌آید:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{line} (\frac{\lambda dl}{r^2})\overrightarrow{r}$$

گفتیم حلقه‌ را به بخش‌های بسیار کوچکی به شکل کمان تقسیم می‌کنیم. فرض کنید کمان انتخابی بین $$\theta$$ و $$\theta + d \theta$$ باشد، بنابراین طول آن برابر $$R d \theta$$ و مقدار بار آن برابر $$\lambda R d \theta$$ خواهد بود. همچنین، فاصله کمان کوچک از نقطه P برابر $$\sqrt {z^2 + R^2}$$ و زاویه $$\phi$$ برابر $$\cos \phi = \frac{z}{\sqrt{z^2 + R^2}}$$ است. در نتیجه، میدان الکتریکی به صورت زیر محاسبه خواهد شد:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{line} (\frac{\lambda dl}{r^2})\overrightarrow{r} = \frac{1}{4 \pi \epsilon_0}\int_{0}^{2 \pi} \frac{\lambda R \ d \theta}{z^2 + R^2} \frac{z}{\sqrt{z^2 + R^2}}\ \overrightarrow{z} \\ = \frac{1}{4 \pi \epsilon_0} \frac{\lambda R z}{(z^2 + R^2)^{\frac{3}{2}}}\ \overrightarrow{z}\int_{0} d \theta \\ = \frac{1}{4 \pi \epsilon_0}\frac{2 \pi \lambda R z}{(z^2 +R^2)^{\frac{3}{2}}} \ \overrightarrow{z} \\ = \frac{1}{4 \pi \epsilon_0}\frac{q_{tot} z}{(z^2 +R^2)^{\frac{3}{2}}} \ \overrightarrow{z}$$

همان‌طور که در حل دو مثال بالا دیدیم، تقارن نقش مهمی در ساده‌سازی آن‌ها دارد. اگر $$z$$ در مقایسه با شعاع دایره بسیار بزرگ‌تر باشد، میدان الکتریکی ناشی از حلقه به صورت زیر ساده می‌شود:

$$\overrightarrow{E}\approx \frac{1}{4 \pi \epsilon_0}\frac{q_{tot}}{z^2} \ \overrightarrow{z}$$

مثال محاسبه میدان الکتریکی قرص رسانا

قرصی دایره‌ای به شعاع R و چگالی سطحی بار یکنواخت $$\sigma$$ را در صفحه xy در نظر بگیرید. میدان الکتریکی را در فاصله z از قرص و بالای مرکز آن به‌دست آورید.

پاسخ: میدان الکتریکی حاصل از بار سطحی به صورت زیر به‌دست می‌آید:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{surface} (\frac{\sigma dA}{r^2})\overrightarrow{r}$$

برای حل این مثال، قرص را به حلقه‌های بسیار کوچکی هم‌مرکز با قرص تقسیم می‌کنیم.

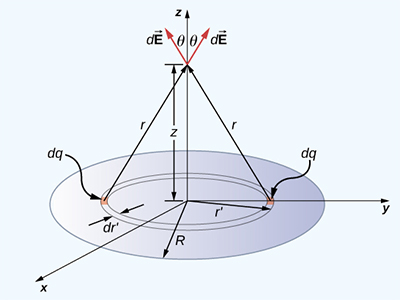
مولفه‌های افقی میدان الکتریکی به دلیل تقارن، یکدیگر را خنثی می‌کنند. بنابراین، جهت میدان کل در راستای محور z خواهد بود. مولفه عمودی میدان الکتریکی به صورت زیر به‌دست می‌آید:

$$\overrightarrow{E} (P) = \frac{1}{4 \pi \epsilon_0} \int_{surface} (\frac{\sigma dA}{r^2})\ \cos \theta \ \overrightarrow{k}$$

کمیت‌های نامشخص را بر حسب کمیت‌های داده شده در مثال می‌نویسیم:

$$dA = 2 \pi r' dr' \\ r^2 = r'^2 + z^2 \\ \cos \theta = \frac{z}{(r'^2 + z^2)^{\frac{1} {2}}}$$

به این نکته توجه داشته باشید که $$r$$ برابر فاصله حلقه کوچک فرضی از نقطه P و $$r'$$ فاصله مرکز قرص از حلقه است.

با جایگزین کردن عبارت‌های بالا در انتگرال، داریم:

$$\overrightarrow{E} (P) = \overrightarrow{E} (z) \\ = \frac{1}{4 \pi \epsilon_0} \int_{0}^{R} \frac{\sigma ( 2 \pi r' dr') z }{(r'^2 + z^2) ^ {\frac{3}{2}}} \ \overrightarrow{k} \\ = \frac{1}{4 \pi \epsilon_0} (2 \pi \sigma z) (\frac{1}{z}- \frac{1}{\sqrt{R^2 + z^2}})\ \overrightarrow{k} \\ \overrightarrow{E}(z) = \frac{1}{4 \pi \epsilon_0}( 2\pi \sigma - \frac{2 \pi \sigma z}{\sqrt{R^2 + z^2}}) \ \overrightarrow{k}$$

اگر $$z$$ بسیار بزرگ‌تر از شعاع قرص باشد، میدان الکتریکی به صورت زیر ساده می‌شود:

$$\overrightarrow{E} (z) \approx \frac{1}{4 \pi \epsilon_0}\frac{\sigma \pi R^2}{z^2} \ \overrightarrow{k}$$

اگر به جای قرص از مستطیلی با بار سطحی یکنواخت استفاده شود، میدان الکتریکی به چه شکلی خواهد بود؟

هنگامی که $$R \rightarrow \infty$$ می‌رود، قرص به صفحه‌ای تخت و بی‌نهایت تبدیل می‌شود که مساحت آن بسیار بزرگ‌تر از ضخامت آن و $$z$$ است:

$$\overrightarrow{E} = \lim_{R \rightarrow \infty}\ \frac{1}{4 \pi \epsilon_0}(2 \pi \sigma - \frac{2 \pi \sigma z}{\sqrt{R^2 + z^2}}) \ \overrightarrow{k} = \frac{\sigma}{2 \epsilon_0} \ \overrightarrow{k}$$

به این نکته توجه داشته باشید که میدان الکتریکی حاصل از صفحه بی‌نهایت با چگالی سطحی بار یکنواخت، ثابت است.

مثال محاسبه میدان دو صفحه بی‌ نهایت

دو صفحه موازی با چگالی سطحی بار یکسان ولی با علامت‌ مخالف به صورت زیر، در تصویر نشان داده شده است. میدان الکتریکی حاصل از این دو صفحه را در هر نقطه‌ای از فضا به‌دست آورید.

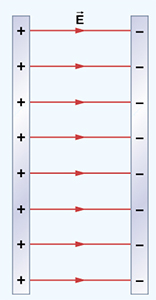
پاسخ: در مطالب بالا، میدان حاصل از صفحه تخت بی‌نهایت را به‌دست آوردیم. بنابراین، با استفاده از اصل برهم‌نهی میدان حاصل از دو صفحه را حساب خواهیم کرد. در ابتدا، نقطه‌ای دلخواه را بیرون دو صفحه و نزدیک به صفحه با بار سطحی مثبت، انتخاب می‌کنیم.

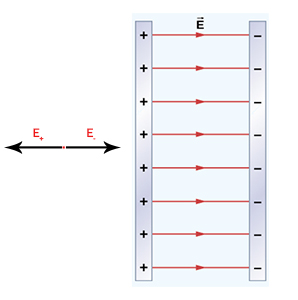
همان‌طور که از در تصویر نشان داده شده است، میدان حاصل از دو صفحه در خلاف جهت یکدیگر قرار دارند و از نظر بزرگی با یکدیگر برابر هستند. در نتیجه، اندازه میدان کلی در خارج دو صفحه برابر صفر است. اگر نقطه انتخابی در ناحیه بین دو صفحه باشد، میدان حاصل از دو صفحه با یکدیگر جمع خواهند شد، بنابراین اندازه میدان کلی برابر است با:

$$\overrightarrow{E} = \frac{\sigma}{\epsilon_0}\ \overrightarrow{i}$$

اگر علامت بار سطحی دو صفحه با یکدیگر برابر باشد، میدان الکتریکی کل در ناحیه بین صفحات برابر صفر و در خارج آن‌ها برابر $$\overrightarrow{E} = \frac{\sigma}{\epsilon_0}\ \overrightarrow{i}$$ خواهد بود.

چرا بارها روی سطح رسانا قرار می گیرند ؟

پوسته‌ کروی خنثی به شکل زیر را در نظر بگیرید.

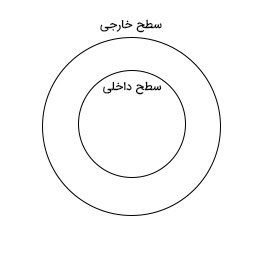
فرض کنید به روش دلخواهی، الکترون‌ها را از داخل پوسته خارج می‌کنیم. در نتیجه، با خروج الکترون‌ها از داخل پوسته، بار آن مثبت خواهد شد. می‌دانیم بارهای همنام یکدیگر را دفع می‌کنند، از این رو بارهای مثبت یکدیگر را دفع خواهند کرد. بنابراین، بارهای مثبت تا جایی که امکان دارد از یکدیگر دور و در نهایت، ساکن می‌شوند. اما سوالی که ممکن است مطرح شود آن است که چه زمانی بارهای مثبت ساکن می‌شوند یا به بیان دیگر به شرایط الکترواستاتیک می‌رسیم. آرایش نهایی این بارها بسیار مهم است. برای رسیدن به پاسخ این سوال آرایش‌های مختلفی را در نظر می‌گیریم.

• آرایش اول
  • فرض کنید، بارهای مثبت در همه جای رسانا، پوسته داخلی، پوسته خارجی و داخل آن، توزیع می‌شوند.
• آرایش دوم
  • فرض کنید بارهای مثبت بر روی سطح داخلی و خارجی پوسته قرار می‌گیرند.
• آرایش سوم
  • فرض کنید بنا به دلایلی، تمام بارهای مثبت بر روی سطح خارجی پوسته قرار می‌‌گیرند.

در ادامه، هر یک از آرایش‌های گفته شده را بررسی می‌کنیم. می‌دانیم در شرایط الکترواستاتیک، مقدار میدان الکتریکی داخل رسانا برابر صفر است. در نتیجه، مقدار میدان الکتریکی را در هر یک از آرایش‌های داده شده بررسی و برای تعیین میدان الکتریکی از قانون گاوس استفاده می‌کنیم. بر طبق این قانون، شار عبوری از هر سطح بسته به صورت زیر به‌دست می‌آید:

$$\Phi _{closed} = \frac{q_{in}}{\epsilon _ 0}$$

بنابراین، اگر مقدار بار کلی در هر سطح بسته دلخواهی برابر $$q$$ باشد، شار عبوری از آن سطح مخالف صفر است. بنابراین، میدان الکتریکی داخل سطح بسته نیز مخالف صفر خواهد بود. ابتدا آرایش اول را در نظر می‌گیریم، و سطح بسته‌ای را داخل پوسته رسم می‌کنیم. همان‌طور که در تصویر زیر دیده می‌شود، مقدار بار کل داخل سطح بسته مخالف صفر است. از این رو، شار گذرنده از این سطح مثبت و مخالف صفر خواهد بود. در نتیجه، مقدار میدان الکتریکی داخل رسانا مخالف صفر است. بر طبق قانون گاوس، میدان الکتریکی داخل رسانا برابر صفر خواهد بود. بنابراین، آرایش اول حذف می‌شود.

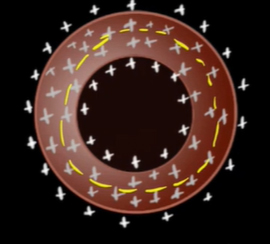
در ادامه آرایش دوم را در نظر می‌گیریم و سطح بسته‌ای را داخل رسانا به صورت زیر رسم می‌کنیم.

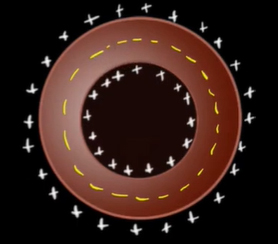
همان‌گونه که می‌بینیم، مقدار بار کل داخل این سطح مخالف صفر است. در نتیجه، شار عبوری از سطح و میدان الکتریکی داخل رسانا مخالف صفر خواهند بود. از این رو، آرایش دوم نیز حذف می‌شود. با حذف دو آرایش نخست، نتیجه می‌گیریم که بارها نه داخل حجم پوسته و نه روی سطح داخلی آن، جمع می‌شوند.

تنها آرایش باقی‌مانده، آرایش سوم است. مشابه دو حالت قبل، سطح بسته‌ای را داخل رسانا رسم می‌کنیم. همان‌طور که در تصویر زیر دیده می‌شود، مقدار بار کل داخل سطح صفر است. بنابراین، شار عبوری از سطح و میدان الکتریکی داخل رسانا برابر صفر خواهند بود. در نتیجه، آرایش سوم از نظر فیزیکی صحیح است.

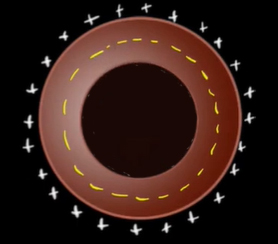
نکته: بارهای الکتریکی در رسانا همواره بر روی سطح خارجی توزیع می‌شوند.

تعیین چگالی سطحی بار در پوسته کروی

چگالی سطحی بار کره‌ای برابر $$\sigma$$ است. اگر این کره توسط پوسته‌ کروی نارسانا احاطه شده باشد، چگالی سطحی بار پوسته کروی برابر است با:

1. $$\sigma$$
2. $$- \ \sigma$$
3. صفر
4. $$\frac {\sigma}{2}$$

پاسخ: کره‌ای با بار سطحی $$\sigma$$ را در مرکز پوسته کروی نارسانا قرار می‌دهیم.

فرض می‌کنیم شعاع کره برابر $$R_1$$ و شعاع داخلی پوسته برابر $$R_2$$ باشد. همان‌گونه که در مطالب بالا گفتیم، چگالی سطحی بار برابر نسبت بار کل بر مساحت است. بنابراین، چگالی سطحی کره به صورت زیر نوشته می‌شود:

$$\sigma = \frac{Q}{4 \pi R_1^2}$$

مقدار بار کل کره برابر است با:

$$Q_ {tot} = \sigma (4 \pi R_1^2)$$

از آنجا که پوسته کروی نارسانا است، القایی صورت نخواهد گرفت. بنابراین، مقدار بار کل پوسته نارسانا برابر صفر خواهد بود. پاسخ صحیح، گزینه ۳ است.

تعیین چگالی سطحی بار نیمکره

اگر کره‌ فلزی بارداری را به دو قسمت نامساوی A و B تقسیم کنیم، به گونه‌ای که مساحت قسمت A بیشتر از مساحت قسمت B باشد، کدام یک از گزینه‌های زیر در مورد چگالی سطحی بار صحیح است:

1. چگالی سطحی بار قسمت A بیشتر از قسمت B است.
2. چگالی سطحی بار قسمت B بیشتر از قسمت A است.
3. چگالی سطحی بار قسمت A و B با یکدیگر برابر هستند.
4. هیچ‌کدام

پاسخ: همان‌طور که در مطالب بالا گفته شد، چگالی سطحی بار با استفاده از رابطه زیر به‌دست می‌آید:

$$\sigma = \frac {Q} {A}$$

بار داده شده به جسم فلزی متقارن، به صورت یکنواخت بر روی سطح آن پخش می‌شود. بنابراین، چگالی سطحی بار جسم فلزی متقارن همواره در تمام نقاط یکنواخت خواهد بود. در نتیجه، پاسخ صحیح گزینه ۳ است.

تعیین چگالی سطحی بار و میدان الکتریکی داخل رسانای کروی با حفره

کره‌ای رسانا با شعاع R در نظر بگیرید. داخل کره حفره‌ای با شعاع a ایجاد می‌کنیم و در مرکز آن بار نقطه‌ای q قرار می‌دهیم.

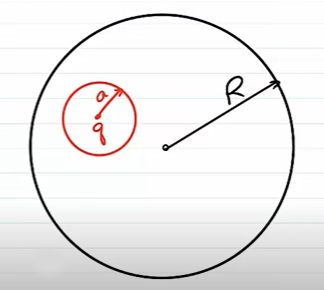
۱) چگالی سطحی بار حفره ($$\sigma_a$$) و کره ($$\sigma_R$$) را به‌دست آورید.

گفتیم میدان الکتریکی داخل رسانا برابر صفر است، بنابراین، مقدار بار القایی بر روی حفره برابر $$- \ q$$ خواهد بود. $$\sigma_a$$ به صورت زیر به‌دست می‌آید:

$$\sigma _a = \frac{-q}{4 \pi a^2}$$

مقدار بار القایی بر روی کره بزرگ برابر $$+ \ q$$ است. در نتیجه، $$\sigma_R$$ برابر است با:

$$\sigma _a = \frac{q}{4 \pi R^2}$$

۲) میدان الکتریکی را در نقاط مختلف فضا به‌دست آورید.

برای به‌دست آوردن میدان الکتریکی در نقاط مختلف از قانون گاوس استفاده می‌کنیم.

در ابتدا میدان الکتریکی را داخل حفره به‌دست می‌آوریم ($$r$$):

$$\int \overrightarrow{E}.d \overrightarrow{a} = \frac{Q_{enc}}{\epsilon_0}$$

$$da$$ برابر مساحت سطح بسته داخل حفره است.

$$E \ 4 \pi r^2 = \frac{q}{\epsilon_0} \\ E_c = \frac{q}{4 \pi \epsilon_0 r^2}$$

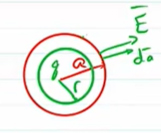
جهت این میدان در راستای شعاع حفره و به سمت خارج آن است.

در ادامه، میدان الکتریکی را خارج از کره به‌دست می‌آوریم ($$r>R$$):

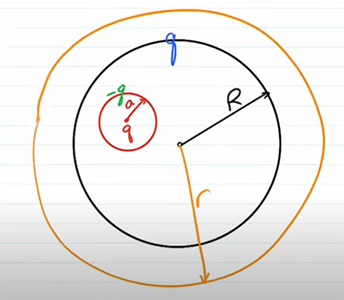
مقدار بار داخل سطح بسته برابر $$q$$ است.

$$\int \overrightarrow{E}.d \overrightarrow{a} = \frac{Q_{enc}}{\epsilon_0}$$

با قرار دادن $$q$$ به جای $$Q_{enc}$$ در رابطه بالا، میدان الکتریکی به صورت زیر به‌دست خواهد آمد:

$$E \ 4 \pi r^2 = \frac{q}{\epsilon_0} \\ E_c = \frac{q}{4 \pi \epsilon_0 r^2}$$

در پایان، میدان الکتریکی را داخل کره به‌دست می‌آوریم ($$a$$):

بر طبق قانون گاوس می‌دانیم، میدان الکتریکی داخل رسانا برابر صفر است. بنابراین، بزرگی میدان داخل کره رسانا صفر خواهد بود.

جمع‌بندی

در این مطلب مبحث‌های زیر را با حل مثال آموختیم:

• تعریف چگالی سطحی بار با ذکر مثال
• تعریف چگالی خطی بار با ذکر مثال
• تعریف چگالی حجمی بار با ذکر مثال
• محاسبه میدان الکتریکی چگالی بارهای مختلف