خمیدگی منحنی مسطح — به زبان ساده
در این مطلب از مجموعه آموزشهای ریاضی مجله فرادرس، با خمیدگی منحنی در صفحه و شعاع خمیدگی آشنا میشویم.
خمیدگی منحنی
منحنی یا خم مسطح $$ C $$ را میتوان به صورت پارامتری با بردار شعاعی $$ \mathbf{r}\left( t \right) $$ تعریف کرد.
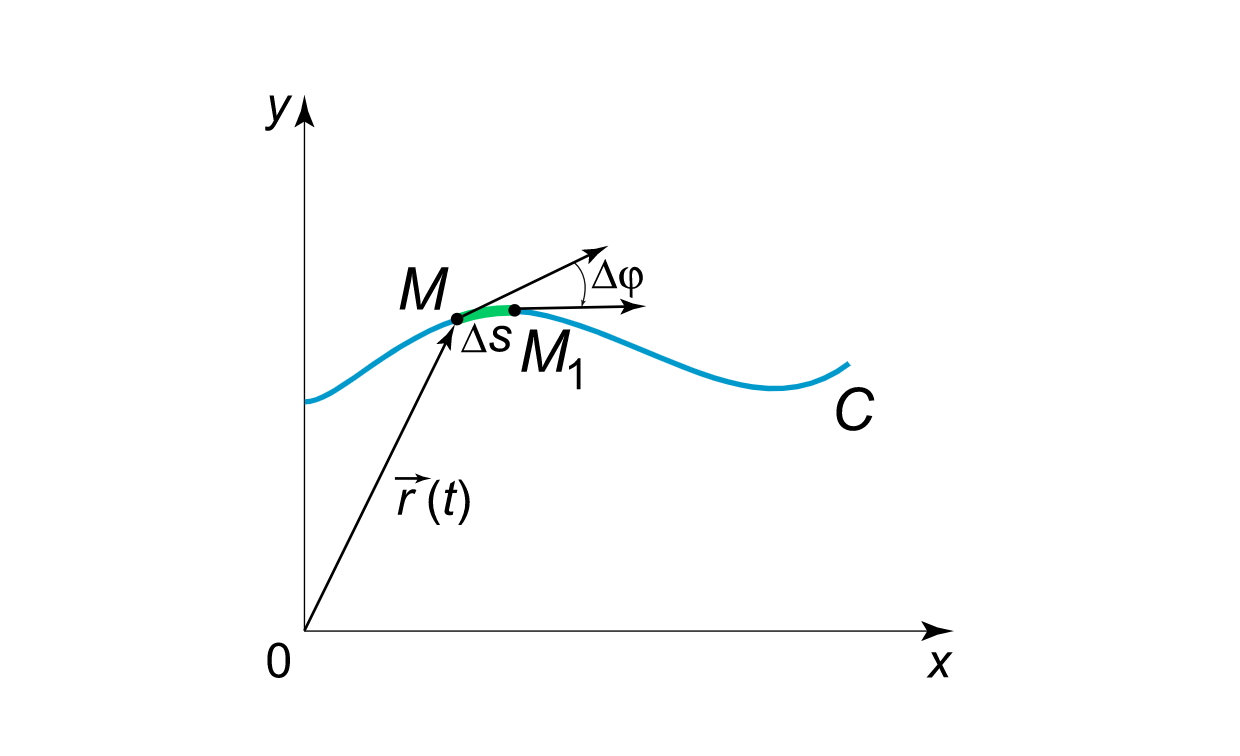
وقتی نقطه $$ M$$ در طول منحنی $$ C $$ حرکت میکند، جهت خط مماس یا شیب تغییر خواهد کرد (شکل ۱).
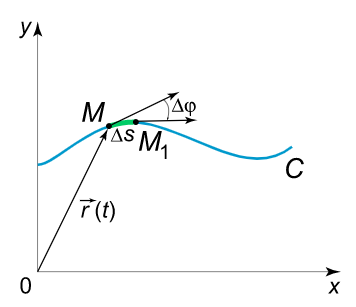
انحنا یا خمیدگی منحنی را میتوان به عنوان نسبت زاویه چرخش $$\Delta \varphi$$ خط مماس نسبت به طول $$\Delta s = M{M_1}$$ کمان یا قوس پیموده شده تعریف کرد. این نسبت $$\large\frac{{\Delta \varphi }}{{\Delta s}}\normalsize $$ خمیدگی میانگین یا متوسط منحنی نامیده میشود. وقتی نقطه $$ M _ 1 $$ به نقطه $$ M $$ نزدیک میشود، خمیدگی منحنی در نقطه $$ M $$ به دست میآید:
$$ \large k = \lim \limits _ { \Delta s \to 0 } \frac { { \Delta \varphi } } { { \Delta s } } = \frac { { d \varphi } } { { d s } } . $$
واضح است که خمیدگی $$ k $$ در حالت کلی، بسته به جهت چرخش مماس، مثبت یا منفی است.
اگر یک منحنی با بردار شعاعی $$\mathbf{r}\left( t \right) $$ تعریف شده باشد، خمیدگی به صورت زیر خواهد بود:
$$ \large k = \frac { { \mathbf { r’ } \times \mathbf { r ^ { \prime \prime } } } } { { { { \left | { \mathbf { r’ } } \right | } ^ 3 } } } , $$
که $$\mathbf{r}’$$ و $$\mathbf{r}^{\prime\prime} $$ مشتقهای اول و دوم بردار شعاعی هستند.
اگر مختصات یک منحنی با تابع صریح $$ y = f ( x ) $$ داده شده باشد، خمیدگی با فرمول زیر محاسبه میشود:
$$ \large k = \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$
در حالتی که منحنی در مختصات قطبی به فرم $$\rho = \rho \left( \varphi \right) $$ داده شده باشد، خمیدگی $$ k $$ با عبارت زیر تعریف میشود:
$$ \large { k \left ( \varphi \right ) } = { \frac { { { \rho ^ 2 } + 2 { { \left ( { \rho’ } \right ) } ^ 2 } – \rho \rho ^ { \prime \prime } } } { { { { \left [ { { \rho ^ 2 } + { { \left ( { \rho’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } $$
خمیدگی منحنی اغلب به عنوان قدر مطلق خمیدگی در نظر گرفته میشود، بدون اینکه جهت چرخش آن در نظر گرفته شود. در این حالت، فرمولهای بالا معتبر هستند، اما قدر مطلق در صورت ظاهر میشود. برای مثال، وقتی مختصات $$ x ( t) $$ و $$ y ( t) $$ یک منحنی به صورت پارامتری داده شده باشند، فرمول خمیدگی به صورت زیر خواهد بود:
$$ \large k = \frac { { \left | { x’ y ^ { \prime \prime } – y’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$
وارون خمیدگی، شعاع خمیدگی نامیده میشود:
$$ \large R = \frac { 1 } { { \left | k \right | } } . $$
دایرهای به این شعاع و مرکز، روی خط قائم داخلی واقع شده است که نزدیکترین تقریب منحنی مسطح در نقطه داد شده است (شکل ۲).
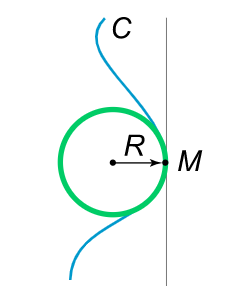
چنین دایرهای، «دایره بوسان» (Osculating Circle) نامیده میشود.
مثالهای خمیدگی منحنی
در این بخش، چند مثال را بررسی خواهیم کرد.
مثال ۱
شعاع خمیدگی یک خط راست را پیدا کنید.
حل: فرض میکنیم معادله صریح خط $$ y = a x + b $$ باشد که در آن، $$ a $$ و $$ b $$ ضرایب ثابت هستند. خمیدگی $$ k $$ و شعاع خمیدگی $$ R $$ این خط راست را محاسبه میکنیم.
قدر مطلق خمیدگی به صورت زیر است:
$$ \large k = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$
و برای خط راست، داریم:
$$ \large { y’ = \left ( { a x + b } \right ) = a , \; \; } \kern-0.3pt { y ^ { \prime \prime } = a’ = 0 . } $$
بنابراین، نتیجه میگیریم که خمیدگی خط راست برابر با صفر و شعاع خمیدگی بینهایت است.
مثال ۲
معادله منحنی پیمایش راهآهن را به دست آورید.
حل: وقتی جسمی به جرم $$ m $$ با سرعت $$ v $$ در طول یک منحنی حرکت کند، یک «نیروی مرکزگرا» (Centripetal Force) به آن اعمال میشود که اندازهاش به شعاع خمیدگی وابسته است:
$$ \large F = \frac{{m{v^2}}}{R}. $$
نیروی مرکزگرا با یک نیروی واکنشی به نام نیروی مرکزگریز (Centrifugal Force) متعادل میشود که برای مثال، مانند مسافرهای یک قطار در هنگام گردش آن عمل میکند. وقتی جسم در طول قوص یک دایره حرکت کند، نیروی مرکزگریز ثابت باقی میماند. برای جلوگیری از ضربات ناگهانی در پیمایش از حرکت خطی به مدور، از مسیرهای پیمایش خاصی استفاده میشود که در آنها خمیدگی به تدریج و به صورت یکنواخت از ۰ تا مقدار نهایی $$\large\frac{1}{R}\normalsize$$ افزایش مییابد.
فرض کنید منحنی پیمایش به قوس $$ OP $$ (شکل ۳) بستگی دارد که طول آن برابر با $$L $$ است.
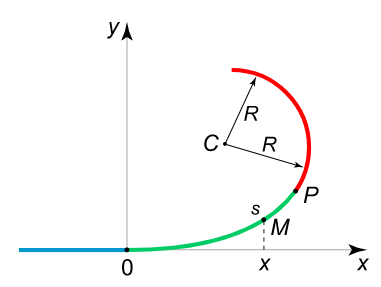
وقتی نقطه $$M$$ در طول این منحنی حرکت کند، شعاع خمیدگی متناسب با مسیر $$ s $$ تغییر میکند:
$$ \large \frac{1}{r} = ms, $$
که $$ m $$ ضریب تناسب است.
این ضریب را میتوان به سادگی از شرایط مرزی به دست آورد: در $$s = OP = L$$، خمیدگی برابر با $$\large\frac{1} {R}\normalsize $$ است:
$$ \large { \frac { 1 } { R } = m L , \; \; } \Rightarrow { m = \frac { 1 } { { L R } } . } $$
در نتیجه، شرط منحنی پیمایش را میتوان با معادله زیر نوشت:
$$ \large { k = \frac { 1 } { r } = \frac { s }{ { L R } } , \; \; } \Rightarrow
{ \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = \frac { s } { { L R } } . } $$
جواب مسئله به سادگی با قرار دادن $$ s = x $$ به دست میآید، که $$ x $$ تصویر $$ M $$ روی محور $$ x $$ است. در این حالت، مشتق $$y' $$ نیز کوچک خواهد بود و میتوانیم در فرمول محاسبه خمیدگی از آن چشمپوشی کنیم. در نتیجه، معادله دیفرانسیل منحنی پیمایش زیر را به دست خواهیم آورد:
$$ \large y ^ { \prime \prime } = \frac { x } { { L R } } . $$
با دو بار انتگرالگیری، جواب عمومی معادله به دست خواهد آمد:
$$ \large { y’ = \frac { { { x ^ 2 } } } { { 2 L R } } + { C _ 1 } , \; \; } \kern-0.3pt
{ y = \frac { { { x ^ 3 } } } { { 6 L R } } + { C _ 1 } x + {C _ 2 } . } $$
با در نظر گرفتن شرایط اولیه $$y\left( {x = 0} \right) = 0 $$ و $$y’\left( {x = 0} \right) = 0$$، معادله منحنی پیمایش نهایی به صورت زیر خواهد بود:
$$ \large y = \frac{{{x^3}}}{{6LR}}, $$
که یک سهمی درجه ۳ است.
مثال ۳
یک منحنی را بیابید که خمیدگی آن ثابت است.
حل: فرض میکنیم معادله منحنی $$ y = y ( x ) $$ باشد. شعاع خمیدگی با فرمول زیر بیان میشود:
$$ \large { R = \frac { 1 } { { \left | k \right | } } } = { \frac { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } } \right | } } . } $$
از آنجا که طبق شرایط مسئله $$ R $$ ثابت است، معادله دیفرانسیل زیر را خواهیم داشت:
$$ \large \frac { { \left | { y ^ { \prime \prime } } \right | } }{ { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = \frac { 1 } { R } . $$
از تغییر متغیر $$y’ = p $$ برای کاهش مرتبه معادله استفاده میکنیم:
$$ \large \frac { { \left | { p’ } \right | } } { { { { \left [ { 1 + { p ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = \frac { 1 } { R } . $$
با تفکیک متغیرها و گرفتن قدر مطلق، خواهیم داشت:
$$ \large { \int { \frac { { d p } } { { { { \left ( { 1 + { p ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } } = { \pm \int { \frac { { d x } } { R } } . } $$
از تغییر متغیر جدید زیر استفاده میکنیم:
$$ \large { p = \tan z , \; \; } \Rightarrow
{ z = \arctan p , \; \; } \Rightarrow
{ d z = \frac { { d p } } { { 1 + { p ^ 2 } } } . } $$
بنابراین، معادله به فرم زیر در میآید:
$$ \large \int { \frac { { d z } } { { \sqrt { 1 + { { \tan } ^ 2 } z } } } } = \pm \int { \frac { { d x } } { R } } . $$
از اتحاد مثلثاتی زیر کمک میگیریم:
$$ \large 1 + { \tan ^ 2 } z = \frac { 1 } { { { { \cos } ^ 2 } z } } , $$
و حاصل انتگرال را محاسبه میکنیم:
$$ \large { \int { \cos z d z } = \pm \int { \frac { { d x } } { R } } , \; \; } \Rightarrow
{ \sin z = \pm \frac { 1 } { R } \left ( { x + { C _ 1 } } \right ) , } $$
که $$ C_ 1 $$ یک ثابت انتگرالگیری است.
با استفاده از رابطه زیر به متغیر $$ p $$ بر میگردیم:
$$ \large \sin z = \sqrt { \frac { { { { \tan } ^ 2 } z } } { { { { \tan } ^ 2 } z + 1 } } } . $$
در اینجا، فقط ریشه مثبت را در نظر میگیریم، زیرا هر دو علامت در سمت راست معادله دیفرانسیل وجود دارند. در نتیجه، معادله به صورت زیر نوشته میشود:
$$ \large { { \left [ { \frac { { { { \tan } ^ 2 } \left ( { \arctan p } \right ) } } { { { { \tan } ^ 2 } \left ( { \arctan p } \right ) + 1 } } } \right ] ^ { \large \frac { 1 } { 2 } \normalsize } } } = { \pm \frac { 1 } { R } \left ( { x + { C _ 1 } } \right ) , \; \; } \Rightarrow
{ \frac { { { p ^ 2 } } } { { { p ^ 2 } + 1 } } = \frac { 1 }{ { { R ^ 2 } } } { \left ( { x + { C _ 1 } } \right ) ^ 2 } . } $$
اکنون معادله را برای متغیر اصلی $$ y$$ مینویسیم:
$$ \large \begin {align*} & \frac { { { { \left ( { y’ } \right ) } ^ 2 } } } { { { { \left ( { y’ } \right ) } ^ 2 } + 1 } } = \frac { 1 } { { { R ^ 2 } } } { \left ( { x + { C _ 1 } } \right ) ^ 2 } , \; \; \Rightarrow
{ { { \left ( { y’ } \right ) ^ 2 } = \frac { 1 } { { { R ^ 2 } } } { \left ( { x + { C _ 1 } } \right ) ^ 2 } \cdot } \kern0pt { \left ( { { { \left ( { y’ } \right ) } ^ 2 } + 1 } \right ) , \; \; } } \\ & \Rightarrow
{ { { \left ( { y’ } \right ) ^ 2 } \left [ { { R ^ 2 } – { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } \right ] } = { { \left ( { x + { C _ 1 } } \right ) ^ 2 } , \; \; } } \Rightarrow
{ { \left ( { y’ } \right )^ 2 } = \frac { { { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } { { { R ^ 2 } – { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } , \; \; } \\ & \Rightarrow
{ y’ = \pm \sqrt { \frac { { { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } { { { R ^ 2 } – { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } } , \; \; } \Rightarrow
{ y = \pm \int { \sqrt { \frac { { { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } { { { R ^ 2 } – { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } } d x } . } \end {align*} $$
برای محاسبه نتیجه انتگرال، از تغییر متغیر زیر بهره میبریم:
$$ \large {x + {C_1} = R\sin t,\;\; }\Rightarrow {dx = R\cos tdt.} $$
انتگرال برابر است با:
$$ \large \begin {align*} y & = \pm \int { \sqrt { \frac { { { { \left ( { x + { C_ 1 } } \right ) } ^ 2 } } } { { { R ^ 2 } – { { \left ( { x + { C _ 1 } } \right ) } ^ 2 } } } } d x }
= { \pm \int { \sqrt { \frac { { { R ^ 2 } \, { { \sin } ^ 2 } t } } { { { R ^ 2 } – { R ^ 2 } \, { { \sin } ^ 2 } t } } } R \cos t d t } }
\\ & = { \pm R \int { \tan t \cos t d t } }
= { \pm R \int { \sin t d t } }
= { \mp R \cos t + { C _ 2 } . } \end {align*} $$
نتیجه را میتوان به صورت زیر نوشت:
$$ \large y + {C_2} = \pm R\cos t. $$
اکنون متغیر $$ t $$ را حذف میکنیم:
$$ \large \begin {align*} & { \sin ^ 2 } t + { \cos ^ 2 } t = 1 , \; \; \Rightarrow
{ \frac { 1 } { { { R ^ 2 } } } { \left ( { x + { C _ 1 } } \right ) ^ 2 } } + { \frac { 1 } { { { R ^ 2 } } } { \left ( { y + { C _ 2 } } \right ) ^ 2 } } = { 1 , \; \; } \\ & \Rightarrow
{ { \left ( { x + { C _ 1 } } \right ) ^ 2 } } + { { \left ( { y + { C _ 2 } } \right ) ^ 2 } } = { { R ^ 2 } . } \end {align*} $$
نتیجه نشان میدهد که منحنیهایی با یک شعاع خمیدگی ثابت $$R$$، مجموعه دوایری با یک مرکز دلخواه و شعاع $$ R $$ هستند.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش ریاضیات عمومی 1
- مجموعه آموزشهای ریاضی و فیزیک
- آموزش ریاضی پایه دانشگاهی
- توابع صعودی و نزولی — به زبان ساده
- مجانب تابع — به زبان ساده
- توابع محدب و مقعر — از صفر تا صد
^^










