انحنا و شعاع انحنا — به زبان ساده

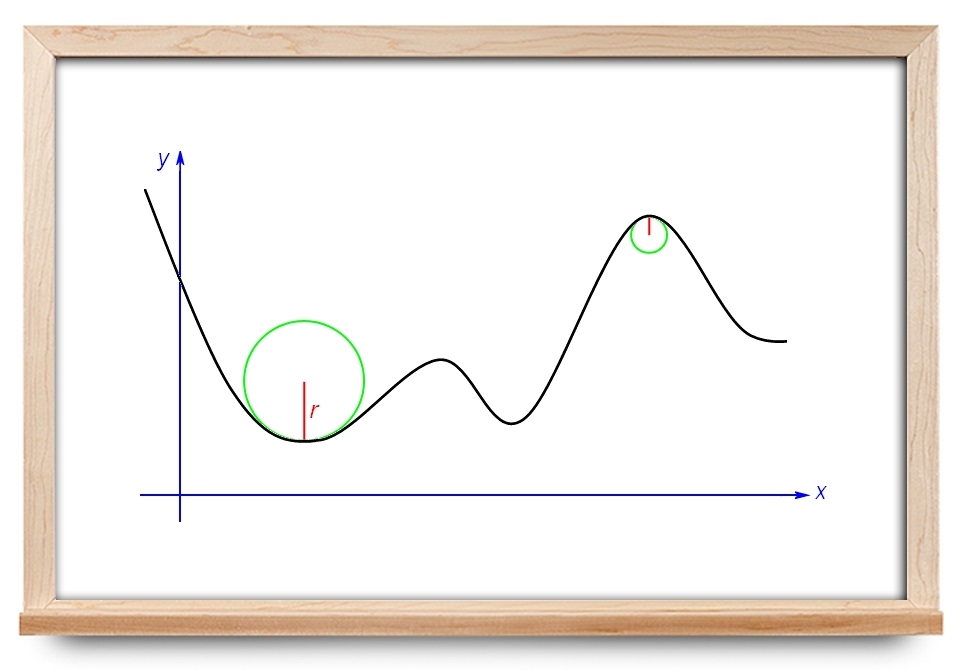
در ادامه مجموعه آموزش‌های ریاضیات مجله فرادرس، در این آموزش به مبحث انحنا و شعاع انحنا می‌پردازیم. در ادامه، ابتدا انحنا را تعریف می‌کنیم، سپس نحوه به دست آوردن شعاع انحنا را بیان خواهیم کرد.

تعریف انحنا و شعاع انحنا

یک منحنی مسطح را در نظر بگیرید که با معادله $$y = f (x)$$ داده شده است. فرض کنید خط مماس بر منحنی در نقطه $$M(x , y )$$ رسم شده باشد.

خط مماس، زاویه $$\alpha$$ را با محور افقی می‌سازد (شکل ۱).

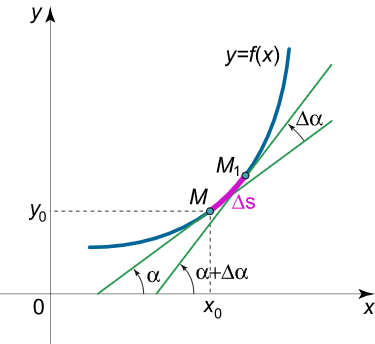
با جابجایی $$\Delta s$$ در طول کمان منحنی، نقطه $$M$$ به سمت نقطه $$M_1$$ حرکت خواهد کرد. در این صورت، موقعیت خط مماس نیز تغییر می‌کند؛ زاویه شیب خط مماس بر نقطه $$M_1$$ و محور مثبت $$x$$، $$\alpha + \Delta\alpha$$ خواهد بود. بنابراین، با حرکت نقطه به اندازه $$\Delta s$$، خط مماس به اندازه $$\Delta \alpha$$ می‌چرخد (فرض شده که وقتی جهت حرکت زاویه $$\alpha$$ پادساعتگرد باشد، افزایشی خواهد بود.)

قدر مطلق نسبت $$\large\frac{{\Delta \alpha }}{{\Delta s}}\normalsize$$ انحنا یا خمیدگی متوسط کمان $$MM_1$$ نامیده می‌شود. با حد $$\Delta s \to 0$$، انحنای منحنی در نقطه $$M$$ به صورت زیر محاسبه می‌شود:

$$\large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | .$$

با توجه به تعریف بالا، انحنای منحنی در یک نقطه، سرعت چرخش خط مماس بر منحنی را در این نقطه نشان می‌دهد.

برای یک منحنی مسطح با معادله $$y = f (x)$$، انحنا در نقطه $$M(x , y )$$ بر حسب مشتق‌های اول و دوم تابع $$f (x)$$ و با فرمول زیر بیان می‌شود:‌

$$\large K = \frac { { \left | { y ^ { \prime \prime } \left ( x \right ) } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ \left ( x \right ) } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } .$$

اگر منحنی به فرم پارامتری و با معادلات $$x = x (t)$$ و $$y = y (t)$$ تعریف شده باشد، آنگاه انحنا در نقطه $$M(x , y )$$ با رابطه زیر تعیین می‌شود:

$$\large K = \frac { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } .$$

اگر منحنی در مختصات قطبی و با معادله $$r = r\left( \theta \right)$$ تعریف شده باشد، انحنا را می‌توان با فرمول زیر محاسبه کرد:

$$\large K = \frac { { \left | { { r ^ 2 } + 2 { { \left ( { r ’ } \right ) } ^ 2 } – r r ^ { \prime \prime } } \right | } } { { { { \left [ { { r ^ 2 } + { { \left ( { r ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } .$$

شعاع انحنای یک منحنی در نقطه $$M(x,y)$$، وارون یا معکوس انحنای $$K$$ نامیده می‌شود:

$$\large R = \frac { 1 } { K } .$$

بنابراین، برای منحنی‌های مسطحی که با معادله صریح $$y = f (x)$$ داده شده‌اند، شعاع انحنا در نقطه $$M(x,y )$$ با عبارت زیر بیان می‌شود:

$$\large R = \frac { { { { \left [ { 1 + { { \left ( { y ’ \left ( x \right ) } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } \left ( x \right ) } \right | } } .$$

مثال‌ها

در این بخش، چند مثال را بیان می‌کنیم.

مثال ۱

انحنا و رئوس بیضی زیر را محاسبه کنید.

 $$\large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1$$

حل: کافی است انحنا را در نقاط $$A (a , 0 )$$ و $$B(0,b)$$ به دست آوریم (شکل ۲)، زیرا با توجه به تقارن منحنی، انحنا در دو رأس مخالف بیضی با هم برابر است.

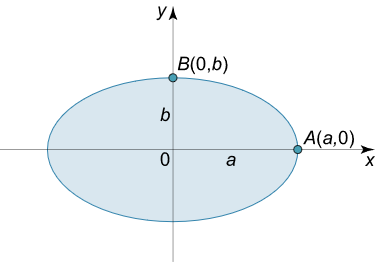
برای محاسبه انحنا، نوشتن فرم پارامتری بیضی محاسبات را ساده‌تر خواهد کرد:

$$\large x = a \cos t , \; \; \; y = b \sin t$$

که در آن، $$t$$‌ یک پارامتر است. مقدار پارامتر در نقطه $$A (a,0)$$ برابر با $$t =0$$ و در نقطه $$B( 0 , b )$$ برابر با $$t = \large\frac{\pi }{2}\normalsize$$ است.

مشتق اول و دوم معادلات به صورت زیر است:

$$\large \begin {align*} x ’ & = { x ’ _ t } = { \left ( { a \cos t } \right ) ^ \prime } = – a \sin t , \; \; \; \kern-0.3pt \\ x ^ { \prime \prime } & = { x ^ { \prime \prime } _ { t t } } = { \left ( { – a \sin t } \right ) ^ \prime } = { – a \cos t ; } \\ y ’ & = { y ’ _ t } = { \left ( { b \sin t } \right ) ^ \prime } = b \cos t , \; \; \; \kern-0.3pt \\ x ^ { \prime \prime } & = { x ^ { \prime \prime } _ { t t } } = { \left ( { b \cos t } \right ) ^ \prime } = – b \sin t . \end {align*}$$

انحنای یک منحنی که با فرم پارامتری توصیف شده، به صورت زیر است:

$$\large K = \frac { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } .$$

با جایگذاری مشتق‌ها در رابطه اخیر، داریم:

$$\large \begin {align*} K & = { \frac { { \left | { a b \, { { \sin } ^ 2 } t + a b \, { { \cos } ^ 2 } t } \right | } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { \left | { a b \left ( { { { \sin } ^ 2 } t + { { \cos } ^ 2 } t } \right ) } \right | } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } } \\ & = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } \end {align*}$$

اکنون مقادیر انحنا را در رئوس $$A (a , 0 )$$ و $$B (0 , b )$$ محاسبه می‌کنیم:

$$\large \begin {align*} K \left ( A \right ) & = K \left ( { t = 0 } \right ) = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } 0 + { b ^ 2 } { { \cos } ^ 2 } 0 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { { \left ( { { b ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { b ^ 3 } } } } = { \frac { a }{ { { b ^ 2 } } } ; } \\ K \left ( B \right ) & = K \left ( { t = \frac { \pi } { 2 } } \right ) = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } \frac { \pi } { 2 } + { b ^ 2 } { { \cos } ^ 2 } \frac { \pi } { 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { { \left ( { { a ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { a ^ 3 } } } } = { \frac { b } { { { a ^ 2 } } } . } \end {align*}$$

مثال ۲

انحنا و شعاع انحنای سهمی $$y = x ^ 2$$ را در مبدأ محاسبه کنید.

حل:‌ ابتدا مشتقات تابع را به صورت زیر می‌نویسیم:

$$\large { y ’ = { \left ( { { x ^ 2 } } \right ) ^ \prime } = 2 x ; } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { 2 x } \right ) ^ \prime } = 2 .}$$

انحنای سهمی با فرمول زیر محاسبه می‌شود:

$$\large { K = \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left [ { 1 + { { \left ( { 2 x } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left ( { 1 + 4 { x ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . }$$

بنابراین، انحنا و شعاع آن در مبدأ ($$x = 0$$) به ترتیب، برابرند با:

$$\large { K \left ( { x = 0 } \right ) = \frac { 2 } { { { { \left ( { 1 + 4 \cdot { 0 ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = 2 , } \; \; \; \kern-0.3pt { R = \frac { 1 } { K } = \frac { 1 } { 2 } . }$$

مثال ۳

انحنا و شعاع انحنای منحنی $$y = \cos mx$$ را در نقطه ماکزیمم آن به دست آورید.

حل: این تابع، در نقطه $$x = {\large\frac{{2\pi n}}{m}\normalsize}$$ به مقدار ماکزیممش می‌رسد که $$n \in Z$$ است. با توجه به متناوب بودن تابع، انحنا در تمام نقاط ماکزیمم مشابه است. بنابراین، کافی است فقط نقطه $$x =0$$ را بررسی کنیم.

مشتق‌های تابع به صورت زیر هستند:

$$\large \begin {align*} y ’ & = { \left ( { \cos m x } \right ) ^ \prime } = – m \sin m x , \\ \; \; \; \kern-0.3pt y ^ { \prime \prime } & = \left ( { – m \sin m x } \right ) ^ \prime = { – { m ^ 2 } \cos m x . } \end {align*}$$

در نتیجه، انحنای این منحنی برابر است با:‌

$$\large \begin {align*} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – { m ^ 2 } \cos m x } \right | } } { { { { \left [ { 1 + { { \left ( { – m \sin m x } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \left | { – { m ^ 2 } \cos m x } \right | } } { { { { \left ( { 1 + { m ^ 2 } { { \sin } ^ 2 } m x } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } . } \end {align*}$$

در نقطه ماکزیمم $$x = 0$$، انحنا و شعاع آن، به ترتیب، برابرند با:

$$\large { { K \left ( { x = 0 } \right ) = \frac { { { m ^ 2 } } } { { { { \left ( { 1 + { m ^ 2 } { { \sin } ^ 2 } 0 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { m ^ 2 } , } } \; \; \; \kern-0.3pt { { R = \frac { 1 } { K } = \frac { 1 } { { { m ^ 2 } } } . } }$$

مثال ۴

انحنا و شعاع انحنای منحنی تابع $$y = \sqrt x$$ را در $$x = 1$$ محاسبه کنید.

حل: مشتقات تابع رادیکالی به صورت زیر هستند:‌

$$\large \begin {align*} y ’ & = { \left ( { \sqrt x } \right ) ^ \prime } = \frac { 1 }{ { 2 \sqrt x } } , \\ \; \; \; \kern-0.3pt y ^ { \prime \prime } & = { \left ( { \frac { 1 } { { 2 \sqrt x } } } \right ) ^ \prime } = { { \left ( {\frac { 1 } { 2 } { x ^ { – \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } } \\ & = { – \frac { 1 } {4 } { x ^ { – \large \frac { 3 } { 2 } \normalsize } } } = { – \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } .} \end {align*}$$

انحنای منحنی با رابطه زیر محاسبه می‌شود:

$$ \large \begin {align*}<br /> \require {cancel} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } \right | } } { { { { \left [ { 1 + { { \left ( { \frac { 1 } { { 2 \sqrt x } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } } { { { { \left ( {1 + \frac { 1 }{ { 4 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } } { { { { \left ( { \frac { { 4 x + 1 } } { { 4 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { { 4 ^ { \large \frac { 3 } { 2 } \normalsize } } \cancel { x ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { 4 \cancel { x ^ { \large \frac { 3 } { 2 } \normalsize } } { { \left ( { 4 x + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left ( { 4 x + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . }<br /> \end {align*} $$

در نقطه $$x = 1$$، مقادیر زیر برای انحنا و شعاع انحنا به دست می‌آید:‌

$$\large \begin {align*} K ( x & = 1 ) = \frac { 2 } { { { { \left ( { 4 \cdot 1 + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = \frac { 2 } { { 5 \sqrt 5 } } , \; \; \; \kern-0.3pt \\ R ( x & = 1 ) = \frac { 1 }{ K } = \frac { { 5 \sqrt 5 } } { 2 } . \end {align*}$$

مثال ۵

منحنی با معادله $${y^2} + {x^3} = 0$$ را در نظر بگیرید. انحنای آن را در نقطه $$( -1 , 1 )$$ به دست آورید.

حل: ابتدا مشتق ضمنی این تابع را می‌نویسیم:

$$\large \begin {align*} { y ^ 2 } + { x ^ 3 } = 0 , \; \; \Rightarrow { { \left ( { { y ^ 2 } + { x ^ 3 } } \right ) ^ \prime } = 0 , \; \; } \\ \Rightarrow { 3 { x ^ 2 } + 2 y y ’ = 0 , \; \; } \Rightarrow { y ’ = – \frac { { 3 { x ^ 2 } } } { { 2 y } } . } \end {align*}$$

به طریق مشابه، مشتق دوم را به دست می‌آوریم:

$$\large \begin {align*} 3 { x ^ 2 } + 2 y y ’ = 0 , \; \; & \Rightarrow { { \left ( { 3 { x ^ 2 } + 2 y y ’ } \right ) ^ \prime } = 0 , \; \; } \\ & \Rightarrow { 6 x + 2 { \left ( { y ’ } \right ) ^ 2 } + 2 y y ^ { \prime \prime } = 0 , \; \; } \\ & \Rightarrow { y y ^ { \prime \prime } + { \left ( { y ’ } \right ) ^ 2 } + 3 x = 0 , \; \; } \\ & \Rightarrow { y ^ { \prime \prime } = – \frac { { { { \left ( { y ’ } \right ) } ^ 2 } + 3 x } } { y } .} \end {align*}$$

با جایگذاری رابطه مشتق اول در رابطه اخیر، داریم:‌

$$\large \begin {align*} y ^ { \prime \prime } & = – \frac { { { { \left ( { y ’ } \right ) } ^ 2 } + 3 x } } { y } = { – \frac { { { { \left ( { – \frac { { 3 { x ^ 2 } } } { { 2 y } } } \right ) } ^ 2 } + 3 x } } { y } } \\ & = { – \frac { { \frac { { 9 { x ^ 4 } } } { { 4 { y ^ 2 } } } + 3 x } } { y } } = { – \frac { { 9 { x ^ 4 } + 1 2 x { y ^ 2 } } } { { 4{ y ^ 3 } } } . } \end {align*}$$

اکنون مقادیر مشتق‌ها را در نقطه $$\left( { – 1,1} \right)$$ محاسبه می‌کنیم:

$$\large \begin {align*} y ’ \left ( { – 1 , 1 } \right ) & = – \frac { { 3 \cdot { { \left ( { – 1 } \right ) } ^ 2 } } } { { 2 \cdot 1 } } = – \frac { 3 } { 2 } , \\ y ^ { \prime \prime } \left ( { – 1 , 1 } \right ) & = \kern0pt { – \frac { { 9 \cdot { { \left ( { – 1 } \right ) } ^ 4 } + 1 2 \cdot \left ( { – 1 } \right ) \cdot { 1 ^ 2 } } } { { 4 \cdot { 1 ^ 3 } } } } = { \frac { 3 } { 4 } . } \end {align*}$$

در نتیجه، انحنای منحنی در نقطه $$(-1 , 1)$$ برابر است با:

$$\large \begin {align*} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } }{ { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \frac { 3 } { 4 } } } { { { { \left [ { 1 + { { \left ( { – \frac { 3 }{ 2 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } } \\ & = { \frac { { \frac { 3 } { 4 } } }{ { { { \left ( { 1 + \frac { 9 } { 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 3 } { 4 } \cdot \frac { { { 4 ^ {\large \frac { 3 } { 2 } \normalsize } } } } { { { {1 3 } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 6 } { { { { 1 3 } ^ { \large \frac { 3 } { 2 } \normalsize } } } } \approx 0.128 . } \end {align*}$$

مثال ۶

انحنای دل‌وار $$r = a\left( {1 + \cos \theta } \right)$$ را در $$\theta = 0$$ محاسبه کنید.

حل: برای محاسبه انحنای منحنی، از فرمول زیر استفاده می‌کنیم:

$$\large K = \frac { { \left | { { r ^ 2 } + 2 { { \left ( { r ’ } \right ) } ^ 2 } – r r ^ { \prime \prime } } \right | } } { { { { \left [ { { r ^ 2 } + { { \left ( { r ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } .$$

مشتق‌های منحنی قطبی برابرند با:

$$\large \begin {align*} r ’ & = { \left [ { a \left ( { 1 + \cos \theta } \right ) } \right ] ^ \prime } = – a \sin \theta , \\ \; \; \; \kern-0.3pt r ^ { \prime \prime } & = { \left ( { – a \sin \theta } \right ) ^ \prime } = – a \cos \theta . \end {align*}$$

با جایگذاری مشتق‌های بالا در معادله انحنا و کمی ساده‌سازی، داریم:

$$\large { K } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { { \left ( { 1 + \cos \theta } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } } . }$$

بنابراین، وقتی $$\theta = 0$$ باشد، منحنی دل‌وار برابر خواهد بود با:

$$\large { K \left ( { \theta = 0 } \right ) } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { { \left ( { 1 + \cos \theta } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } } } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 }{ 2 } \normalsize } } { 2 ^ { \large \frac { 1 } { 2 } \normalsize } } a } } } = { \frac { 3 } { { 4 a } } . }$$

مثال ۷

انحنای دل‌وار $$r = a\left( {1 + \cos \theta } \right)$$ را در $$\theta = 0$$ به دست آورید.

حل: شعاع انحنای منحنی پارامتری با فرمول زیر قابل محاسبه است:

$$\large R = \frac { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } .$$

مشتق‌ها به صورت زیر محاسبه می‌شوند:

$$\large \begin {align*} x ’ & = { \left [ { a \left ( { t – \sin t } \right ) } \right ] ^ \prime } = a \left ( { 1 – \cos t } \right ) , \\ \; \; \; \kern-0.3pt x ^ { \prime \prime } & = { \left [ { a \left ( { 1 – \cos t } \right ) } \right ] ^ \prime } = a \sin t , \\ y ’ & = { \left [ { a \left ( { 1 – \cos t } \right ) } \right ] ^ \prime } = a \sin t , \; \; \; \kern-0.3pt \\ y ^ { \prime \prime } & = { \left ( { a \sin t } \right ) ^ \prime } = a \cos t . \end {align*}$$

با جایگذاری مشتقات بالا در معادله شعاع انحنا، داریم:

$$\large \begin {align*} R & = { \frac { { { { \left [ { 2 { a ^ 2 } \left ( { 1 – \cos t } \right ) } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { { a ^ 2 } \left ( { \cos t – 1 } \right ) } \right | } } } = { \frac { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } { a ^ 3 } { { \left ( { 1 – \cos t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { a ^ 2 } \left ( { 1 – \cos t } \right ) } } } \\ & = { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { \left ( { 1 – \cos t } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } } = { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a \cdot { \left ( { 2 { { \sin } ^ 2 } \frac { t } { 2 } } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } } \\ & = { 4 a { \left ( { { { \sin } ^ 2 } \frac { t } { 2 } } \right ) ^ { \large \frac { 1 } {2 } \normalsize } } . } \end {align*}$$

کمان اول چرخ‌زاد، یعنی بازه $$0 \le t \le 2\pi$$ را در نظر می‌گیریم. شعاع انحنای چرخ‌زاد به صورت زیر بیان می‌شود:

$$\large R = 4 a \sin \frac { t } { 2 } .$$

با توجه به رابطه بالا، مشاهده مي‌کنیم که حداکثر شعاع انحنا در $$t = \pi$$ رخ می‌دهد و مقدار آن برابر است با $${R_{\max }} = 4a$$.

 مثال ۸

انحنای منحنی $$y = \arctan x$$ را در نقاط $$x = 0$$ و بي‌نهایت محاسبه کنید.

حل: مشتقات تابع $$y = \arctan x$$ به صورت زیر هستند:

$$\large y ’ = { \left ( { \arctan x } \right ) ^ \prime } = \frac { 1 } { { 1 + { x ^ 2 } } } , \; \; \; \kern-0.3pt \\ \large { y ^ { \prime \prime } = { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) ^ \prime } } = { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } .}$$

انحنای منحنی معکوس تانژانت به صورت زیر بیان می‌شود:

$$ \large \begin {align*}<br /> K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } \right | } } { { { { \left [ { 1 + { { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } } { { { { \left [ { \frac { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { 2 x { { \left ( { 1 + { x ^ 2 } } \right ) } ^ \cancel { 3 } } } } { { { \cancel { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { 2 x \left ( { 1 + { x ^ 2 } } \right ) } } { { { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac {3 } {2 } \normalsize } } } } . }<br /> \end {align*} $$

همانطور که می‌بینیم، در نقطه $$x = 0$$، انحنا صفر است:

$$\large K \left ( 0 \right ) = { K _ 0 } = 0$$

در این حالت، نقطه $$x = 0$$، نقطه عطف تابع $$y = \arctan x$$ نامیده می‌شود. از آنجایی که مشتق دوم در هر نقطه عطفی برابر با صفر است، انحنا نیز باید برابر با صفر باشد.

اکنون مقدار انحنای $${K_{\infty}}$$ را برای حد $$x \to \infty$$ محاسبه می‌کنیم:

$$\large \begin {align*} { K _ \infty } & = \lim \limits _ { x \to \infty } K \left ( x \right ) = { \lim \limits _ { x \to \infty } \frac { { 2 x \left ( { 1 + { x ^ 2 } } \right ) } } { { { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \lim \limits _ { x \to \infty } \frac { { 2 { x ^ 3 } + 2 x } } { { { { \left ( { { x ^ 4 } + 2 { x ^ 2 } + 2 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \lim \limits _ { x \to \infty } \frac { { \frac { { 2 { x ^ 3 } + 2 x } } { { { x ^ 6 } } } } }{{ \frac { { { { \left ( { { x ^ 4 } + 2 { x ^ 2 } + 2 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { x ^ 6 } } } } } } \\ & = { \lim \limits _ { x \to \infty } \frac { { \frac { 2 } { { { x ^ 3 } } } + \frac { 2 } { { { x ^ 5 } } } } } { { { { \left ( { \frac { { { x ^ 4 } + 2 { x ^ 2 } + 2 } } { { { x ^ 4 } } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \lim \limits _ { x \to \infty } \frac { { \frac { 2 } { { { x ^ 3 } } } + \frac { 2 } { { { x ^ 5 } } } } } { { { { \left ( { 1 + \frac { 2 } { { { x ^ 2 } } } + \frac { 2 } { { { x ^ 4 } } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 0 } { 1 } = 0 . } \end {align*}$$

بنابراین، انحنای منحنی معکوس تانژانت در بی‌نهایت نیز به صفر میل می‌کند. این بدین معنی است که مقدار ماکزیمم انحنا در مقادیر میانی $$x$$ رخ می‌دهد.

مثال ۹

کوچکترین شعاع انحنای تابع نمایی $$y = e ^ x$$ را به دست آورید.

حل: تابع نمایی $$y = e ^ x$$ تنها تابعی است که مشتق‌های آن برابر با خود تابع هستند. بنابراین، می‌توانیم به سادگی فرمول زیر را برای انحنای منحنی بنویسیم:

$$\large { K = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { { e ^ x } } } { { { { \left ( { 1 + { e ^ { 2 x } }} \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . }$$

می‌توان از علامت قدر مطلق در صورت کسر رابطه بالا چشم پوشید، زیرا تابع نمایی همیشه مثبت است.

شعاع انحنا برابر است با:‌

$$\large R = \frac { 1 } { K } = \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { e ^ x } } } .$$

مقدار $$R$$ به مختصه $$x$$ بستگی دارد. بنابراین، $$R$$ تابعی از $$x$$ است و می‌توانیم مقادیر اکسترمم آن را با مشتق‌گیری به دست آوریم:

$$\large \begin {align*} R ’ \left ( x \right ) & = { \left [ { \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { {{ e ^ x } } } } \right ] ^ \prime } \\ & = { \frac { { { e ^ x } { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left [ { 3 { e ^ { 2 x } } – \left ( { 1 + { e ^ { 2 x } } } \right ) } \right ] } } { { { e ^ { 2 x } } } } } \\ & = { \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left ( { 2 { e ^ { 2 x } } – 1 } \right ) } }{ { { e ^ x } } } . } \end {align*}$$

تابع $$R (x)$$ فقط یک نقطه بحرانی دارد:

$$\large \begin {align*} & R ’ \left ( x \right ) = 0 , \; \; \Rightarrow { 2 { e ^ { 2x } } – 1 = 0 , \; \; } \Rightarrow { { e ^ { 2 x } } = \frac { 1 } { 2 } , \; \; } \\ & \Rightarrow { 2 x = \ln \frac { 1 } { 2 } = – \ln 2 , \; \; } \Rightarrow { x = – \frac { { \ln 2 } } { 2 } \approx – 0.35 . } \end {align*}$$

مشتق $$R^\prime\left( x \right)$$ در سمت راست نقطه بحرانی منفی و در سمت راست آن مثبت است. بنابراین، این نقطه یک مینیمم برای تابع $$R(x )$$ است. در این نقطه، تابع نمایی دارای یک شعاع انحنای کمینه است که به صورت زیر محاسبه می‌شود:

$$\large \begin {align*} { R _ { \min } } & = R \left ( { – \frac { { \ln 2 } } { 2 } } \right ) = { \frac { { { { \left [ { 1 + { e ^ { 2 \cdot \left ( { – \large \frac { { \ln 2 } } { 2 } \normalsize } \right ) } } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { {e ^ { – \large \frac { { \ln 2 } } { 2 } \normalsize } } } } } \\ & = { \frac { { { { \left [ { 1 + { e ^ { \ln \large \frac { 1 } { 2 } \normalsize } } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } { { { e ^ { \ln \large \frac { 1 } { { \sqrt 2 } } \normalsize } } } } } = { \frac { { { { \left ( { 1 + \frac { 1 } { 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 1 } { { \sqrt 2 } } } } } = { \sqrt 2 { \left ( { \frac { 3 } { 2 } } \right ) ^ { \large \frac { 3 } { 2 } \normalsize } } \approx 2.60 . } \end {align*}$$

مثال ۱۰

کمینه شعاع انحنای سهمی مرتبه سوم $$y = {x^3}$$ را محاسبه کنید.

حل: مشتق‌های تابع به صورت زیر هستند:‌

$$\large { y ’ = { \left ( { { x ^ 3 } } \right ) ^ \prime } = 3 { x ^ 2 } , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { 3 { x ^ 2 } } \right ) ^ \prime } = 6 x }$$

شعاع منحنی تابع با رابطه زیر به دست می‌آید:‌

$$\large { R = \frac { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } } \right | } } } = { \frac { { {{ \left [ { 1 + { { \left ( { 3 { x ^ 2 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } { { \left | { 6 x } \right | } } } = { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { 6 x } \right | } } . }$$

سهمی مکعب داده شده حول مبدأ متقارن است. به همین دلیل، بخشی از آن را در نظر می‌گیریم که $$x > 0$$ است. بنابراین، با حذف علامت قدر مطلق، مقدار $$R$$ را به صورت تابعی از $$x$$ می‌نویسیم:

$$\large R \left ( x \right ) = \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } }{ { 6 x } } .$$

حال مشتق شعاع انحنا را می‌نویسیم:‌

$$\large \begin {align*} R ’ \left ( x \right ) & = { \left [ { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } }} { { 6 x } } } \right ] ^ \prime } = { \frac { { { { \left ( { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } \right ) } ^ \prime } 6 x – { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } { { \left ( { 6 x } \right ) } ^ \prime } } } { { 3 6 { x ^ 2 } } } } \\ & = { \frac { { 6 { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left [ { 5 4 { x ^ 4 } – \left ( { 1 + 9 { x ^ 4} } \right ) } \right ] } } { { 3 6 { x ^ 2 } } } } = { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left ( { 4 5 { x ^ 4 } – 1 } \right ) } } { { 6 { x ^ 2 } }} . } \end {align*}$$

در $$x > 0$$ تابع فقط یک نقطه بحرانی دارد. محاسبات، منجر به نتیجه زیر می‌شود:‌

$$\large { 4 5 { x ^ 4 } – 1 = 0 , \; \; } \Rightarrow { { x ^ 4 } = \frac { 1 } { { 4 5 } } , \; \; } \Rightarrow { x = \frac { 1 }{ { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } \approx 0.39 . }$$

وقتی از این نقطه بگذریم، $$R’\left( x \right)$$ از منفی به مثبت تغییر علامت می‌دهد. بنابراین، این نقطه متناظر با کوچکترین شعاع انحنا است. مقدار تقریبی این شعاع برابر است با:‌

 $$\large \begin {align*} y ’ \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } } \right ) & = 3 \cdot { \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } \right ) ^ 2 } = \frac { 3 } { { \sqrt { 4 5 } } } , \; \; \; \kern-0.3pt \\ y ^ { \prime \prime } \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } } \right ) & = \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } \end {align*}$$

$$\large \begin {align*} \Rightarrow { R _ { \min } } & = \frac { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } } \right | } } = { \frac { { { { \left [ { 1 + { { \left ( { \frac { 3 } { { \sqrt { 4 5 } } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } } } \\ & = { \frac { { { { \left ( { 1 + \frac { 9 } { { 4 5 } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } } } = { { \left ( { \frac { { 5 4 } } { { 45 } } } \right ) ^ { \large \frac { 3 }{ 2 } \normalsize } } \cdot \frac { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } { 6 } } \\ & = { \frac { { { 2 ^ { \large \frac { 3 }{ 2 } \normalsize } } \cdot { { \left ( { { 3 ^ 3 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot { 5 ^ { \large \frac { 1 } { 4 } \normalsize } } \cdot { { \left ( { { 3 ^ 2 } } \right ) } ^ { \large \frac { 1 } { 4 } \normalsize } } } } { { { { \left ( { { 3 ^ 3 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot { 5 ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot 2 \cdot 3 } } } \\ & = { \frac { { { 2 ^ { \large \frac { 1 } { 2 } \normalsize } } \cdot 3 } } { { { 5 ^ { \large \frac { 5 } { 4 } \normalsize } } } } } = {  \approx 0.5 7 . } \end {align*}$$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• توابع صعودی و نزولی — به زبان ساده
• مجانب تابع — به زبان ساده
• توابع محدب و مقعر — از صفر تا صد

^^