تابع گاما — از صفر تا صد

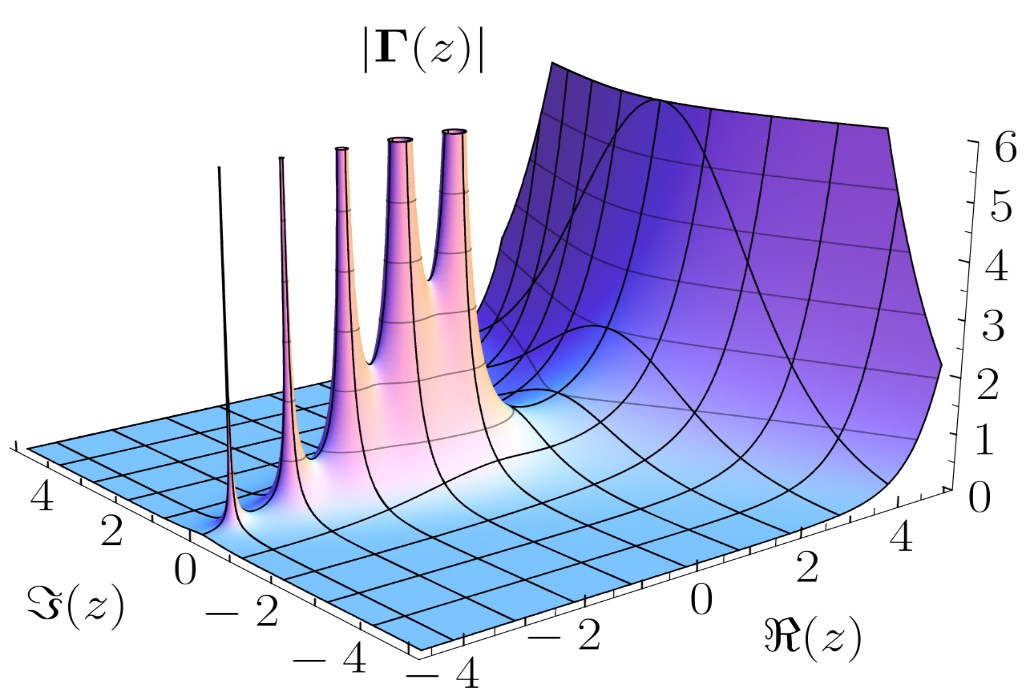
در ریاضیات، تابع گاما ($$  {\displaystyle \Gamma } $$) تعمیمی از تابع فاکتوریل است که به ازای اعداد مختلط نیز قابل تعریف است. شکل کلی یک تابع گاما به‌صورت زیر است:

$$ \large { \displaystyle \Gamma ( n ) = ( n - 1 ) ! \ } $$

این تابع برای اعداد مختلط با مقادیر حقیقی مثبت نیز در قالب رابطه زیر قابل محاسبه است.

$$ \large { \displaystyle \Gamma ( z ) = \int _ { 0 } ^ { \infty } x ^ { z - 1 } e ^ { - x } \, d x ,\ \qquad \Re ( z ) > 0 \ } $$

جالب است بدانید که این تابع در هیچ نقطه‌ای صفر نمی‌شود؛ درنتیجه می‌توان گفت تابع معکوس گاما ($$ \frac { 1 } { \Gamma } $$) تابعی تحلیلی و مختلط است. دیگر بسط‌های مرتبط با تابع فاکتوریل نیز وجود دارند، اما تابع گاما پرکاربردترین و البته مشهور‌ترین آن‌ها است.

منشا تابع گاما

تابع گاما را می‌توان به‌عنوان پاسخ مساله درون‌یابیِ زیر در نظر گرفت.

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

منحنی پیوسته‌ای را بیابید که نقاط طبیعی تابع $$ {\displaystyle y = ( x - 1‌) ! } $$ را به هم متصل کند. با ترسیم چند فاکتوریل اول متوجه می‌شویم که چنین نموداری را می‌توان ترسیم کرد. به نظر می‌رسد که پاسخ این سوال باید به‌صورت منحنی به‌شکل زیر باشد.

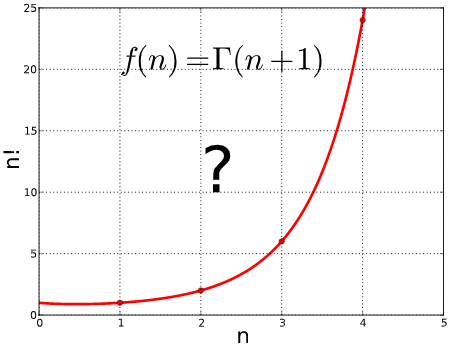
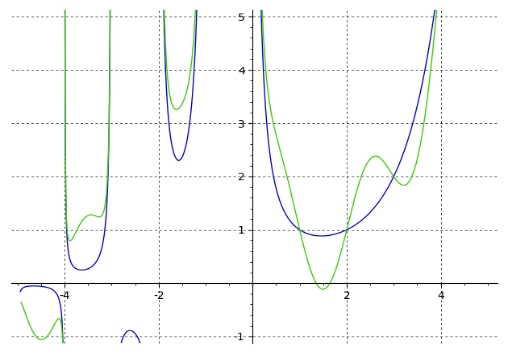
ساده‌ترین رابطه‌ای را که می‌توان حدس زد، $$ { \displaystyle x ! = 1 \times 2 \times \cdots \times x } $$ است. اما این رابطه را نمی‌توان برای توصیف چنین نموداری استفاده کرد، چرا که تنها در اعداد صحیح، نمودار مذکور را به ما می‌دهد. اگر بخواهیم در بین توابع شناخته شده همچون لگاریتم، نمایی یا ترکیب چنین توابعی به دنبال تابعی باشیم که نمودار فوق را نشان دهد به نتیجه‌ای دست نخواهیم یافت. اما با استفاده از مفاهیمی همچون حد یا انتگرال می‌توان به چنین تابعی دست یافت. این تابع همان تابع گاما است. در شکل زیر دو تابع $$ Γ ( z ) $$ و $$ Γ ( z ) + \sin ( π z ) $$ به‌ترتیب با رنگ‌های آبی و سبز نشان داده شده‌اند.

تعریف

همان‌طور که در بالا نیز بیان شد، اگر بخش حقیقی عدد مختلطی همچون $$ z $$ مثبت باشد ($$ { \displaystyle \Re ( z ) > 0 } $$) در این صورت انتگرال زیر به‌عنوان تابع گاما تعریف می‌شود.

$$ \large { \displaystyle \Gamma ( z ) = \int _ { 0 } ^ { \infty } x ^ { z - 1 } e ^ { - x } \, d x } $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

انتگرال فوق مطلقا همگرا بوده و به عنوان انتگرال اویلر نوع دوم شناخته می‌شود. با استفاده از روش انتگرال‌گیری جزء به جزء، می‌توان رابطه زیر را بدست آورد.

$$ \large { \displaystyle { \begin {aligned} \Gamma ( z + 1 ) & = \int
_ { 0 } ^ { \infty } x ^{ z } e ^ {- x } \, d x \\[4pt] & = { \Big [}- x ^ { z } e ^{ - x } { \Big ]} _ { 0 } ^ { \infty } + \int _ { 0 } ^ { \infty } z x ^ { z - 1 } e ^ { - x } \, d x \\[4pt]& = \lim _ { x \to \infty } ( - x ^ { z } e ^ { - x } ) -( 0 e ^ { - 0 } ) + z \int _ { 0 } ^ { \infty } x ^ { z - 1 } e ^ { -x } \, d x \end {aligned} } } $$

با فرض $$ { \displaystyle x \to \infty } $$ عبارت $$ { \displaystyle - x ^ { z } e ^ { - x } \to 0 } $$ برقرار خواهد بود. با استفاده از این گزاره می‌توان رابطه زیر را برای تابع گاما بیان کرد:

$$ \large { \displaystyle { \begin {aligned} \Gamma ( z + 1 ) & = z \int _ { 0 } ^ { \infty } x ^ { z - 1 } e ^ { - x } \, d x \\[6pt]& = z \Gamma ( z ) \end {aligned} }} $$

با استفاده از تعریف فوق، $$ { \displaystyle \Gamma ( 1 ) {\text{}}} $$ برابر می‌شود با:

$$ \large { \displaystyle {\begin{aligned}\Gamma (1)&=\int _ { 0 } ^ { \infty } x ^ { 1 - 1 } e ^ { - x } \, d x \\[6pt] & = { \Big [}-e^{-x}{\Big ]}_{0}^{\infty }\\[6pt] & = \lim _ { x \to \infty } ( - e ^ {- x } ) - ( - e^ { - 0 } ) \\[6pt] & = 0 - ( - 1 ) \\[6pt]&=1\end {aligned} } } $$

بنابراین با فرض $$ { \displaystyle \Gamma ( 1 ) = 1 } $$ و $$ { \displaystyle \Gamma ( n + 1 ) = n \Gamma ( n ) } $$، شکل کلی تابع گاما به ازای تمامی مقادیر طبیعی و مثبت $$ n $$ به‌صورت زیر بدست می‌آید.

$$ \large { \displaystyle \Gamma ( n ) = 1 \cdot 2 \cdot 3 \cdots ( n - 1 ) = ( n - 1 ) ! } $$

جالب است بدانید از تعریف فوق می‌توان به‌منظور اثبات استدلال استقرایی نیز بهره برد. همان‌طور که مشاهده می‌کنید رابطه بدست آمده در بالا نشان‌دهنده همان فاکتوریل است.

دیگر تعاریف

به‌منظور محاسبه $$ z ! $$ به ازای مقداری مختلط از $$ z $$، مناسب است که در ابتدا مقدار $$ n ! $$ را به ازای عددی بزرگ و مشخص از $$ n $$ بیابیم. در این صورت می‌توان مقدار $$  {\displaystyle ( n + z ) ! } { } $$ را حدس زده و با $$ n $$ بار استفاده از رابطه $$ { \displaystyle m ! = m ( m - 1 ) ! } $$ به $$ z ! $$ رسید. از طرفی می‌توان گفت این مقدار با میل کردن $$ n $$ به بینهایت، به عددی دقیق نزدیک می‌شود. از طرفی به ازای مقداری ثابت از $$ m $$ این گزاره را می‌توان به زبان ریاضی، به‌صورت زیر بیان کرد:

$$ {\displaystyle \lim _ { n \to \infty } { \frac { n ! \; ( n + 1 ) ^ { m } }{ ( n +m ) ! } } = 1 \, } $$

اگر $$ m $$ مقداری طبیعی نباشد، در این صورت نمی‌توان گفت الزاما گزاره فوق درست است چراکه تاکنون (تا این قسمت از مقاله) تابع فاکتوریل را برای اعداد غیرطبیعی تعریف نکرده‌ایم. به‌منظور تعریف کردن فاکتوریل برای مقادیر مختلط، در ابتدا حد بیان شده در بالا را در نظر بگیرید.

$$ {\displaystyle \lim _ { n \to \infty } { \frac { n ! \; ( n + 1 ) ^ { m } }{ ( n +m ) ! } } = 1 \, } $$

طرفین این رابطه را در $$ z ! $$ ضرب کنید. در این صورت مقدار $$ z ! $$ مطابق با رابطه زیر بدست می‌آید.

$$ { \displaystyle { \begin {aligned} z ! & = \lim _ { n \to \infty } n ! { \frac { z ! } { ( n + z ) ! } } ( n + 1 ) ^ { z } \\[8pt]& = \lim _ { n \to \infty } ( 1 \cdots n ) { \frac { 1 } { ( 1 + z ) \cdots ( n + z ) } } \left [\left ( 1 + { \frac {1 } { 1 } } \right ) \left ( 1+{\frac {1}{2 } } \right ) \cdots \left ( 1 + { \frac { 1 } { n } } \right ) \right] ^ { z } \\[8pt]& = \prod _ { n = 1 } ^ { \infty }\left[{\frac { 1 } { 1 + { \frac { z } { n } } } } \left( 1 + { \frac {1} { n } } \right ) ^ { z } \right] \end {aligned} } } $$

عبارت فوق به جزء در موارد اعداد طبیعی منفی، دارای پاسخ است. دلیل این امر نیز آن است که به منظور محاسبه مقدار فوق باید از رابطه $$ { \displaystyle m ! = m ( m - 1 ) ! } $$ به‌صورت بازگشتی استفاده کرد که این امر منجر به ایجاد عدد صفر در مخرج کسر می‌شود. به همین‌ صورت تابع گامای ارائه شده در زیر نیز به ازای تمامی مقادیر از $$ z $$ به‌غیر از اعداد طبیعی منفی برقرار هستند.

$$ { \displaystyle \Gamma ( z ) = { \frac { 1 } { z } } \prod _ { n =1 } ^ { \infty } { \frac { \left ( 1 + { \frac { 1 } { n } } \right ) ^ { z } } { 1 +{ \frac { z } { n } } } } \, } $$

حد بیان شده در بالا را برای تابع گاما نیز می‌توان بیان کرد.

$$ { \displaystyle \lim _ { n \to \infty } { \frac { \Gamma ( n + z ) }{ \Gamma ( n ) \; n ^ { z } } } = 1 } $$

تعریف وایراشتراس

تعریف وایراشتراس از تابع گاما نیز به ازای تمامی مقادیر مختلط به‌جز اعداد طبیعی منفی درست است. این تعریف به‌صورت زیر بیان می‌شود.

$$ { \displaystyle \Gamma (z)={\frac { e ^ { - \gamma z } } { z } } \prod _ { n = 1 } ^ { \infty } \left ( 1 + { \frac { z } { n } } \right ) ^ { - 1} e ^ { z / n } } $$

در رابطه فوق مقدار گاما برابر است است با:

$$ { \displaystyle \gamma \approx 0 .5 7 7 2 16 } $$

البته تابع گامای ناکامل را نیز می‌توان به‌صورت زیر و به‌شکل حاصل جمع بیان کرد:

$$ { \displaystyle \Gamma ( z , x ) = x ^ { z } e ^ { - x } \sum _ { n = 0 } ^ { \infty } { \frac { L _ { n } ^ { (z ) } ( x ) } { n + 1 } } } $$

البته این تابع به ازای مقادیر حقیقی بیشتر از ۱- و مقادیر مثبت $$ x $$ دارای پاسخ است. هم‌چنین شکل نامعمول تابع گاما که به ازای مقادیر حقیقی بیشتر از $$ 0.5 $$ دارای پاسخ است را می‌توان در قالب رابطه زیر نیز بیان کرد:

$$ { \displaystyle \Gamma ( z ) = t ^ { z } \sum _ { n = 0 } ^ { \infty } { \frac { L _ {n } ^ { (z ) } (t ) } { z + n } } \,‌} $$

توابع مبتنی بر تابع گاما

تابع گاما را می‌توان در قالب تابعی تحت عنوان معادله بازتابی اویلر، به‌صورت زیر بیان کرد:

$$ { \displaystyle \Gamma ( 1 - z ) \Gamma ( z ) = { \pi \over \sin ( \pi z ) } , \qquad z \not \in \mathbb { Z } } $$

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

رابطه فوق را می‌توان به ازای مقادیر اندک $$ \epsilon $$ به‌شکل زیر نیز بیان کرد:

$$ \Gamma ( \varepsilon - n ) = ( - 1 ) ^ { n -1 } \; { \frac { \Gamma ( - \varepsilon ) \Gamma ( 1 + \varepsilon ) } { \Gamma ( n + 1 -\varepsilon ) } } $$

معادله تکراری لژاندر را نیز می‌توان در قالب رابطه زیر بیان کرد (اثبات این دو رابطه در منبع همین مقاله ارائه شده‌اند):

$$ { \displaystyle \Gamma ( z ) \Gamma \left ( z + { \tfrac { 1 }{ 2 } } \right ) = 2 ^ { 1 - 2 z } \; { \sqrt { \pi } } \;\Gamma ( 2 z ) } $$

معادله تکراری، حالت خاصی از قضیه ضرب است که در ادامه ارائه شده است.

$$ { \displaystyle \prod _ { k = 0 } ^ { m - 1 } \Gamma \left ( z + { \frac { k } { m } } \right ) = ( 2 \pi ) ^ { \frac { m - 1 } { 2 } } \; m^
{ { \frac { 1 } { 2 } }- m z } \; \Gamma ( m z ) } $$

ویژگی ساده اما مفید که می‌توان آن را از تعریف حد برداشت کرد، به‌صورت زیر قابل بیان است:

$$ { \displaystyle { \overline { \Gamma ( z ) } } = \Gamma ({\overline { z } } ) \; \Rightarrow \;\Gamma ( z ) \Gamma ( { \overline { z } } ) \in \mathbb { R } } $$

با فرض عدد مختلط $$ z $$ به‌صورتِ $$ z = a + bi $$، می‌توان حاصل‌ضرب فوق را به‌صورت زیر نیز بازنویسی کرد:

$$ { \displaystyle { \begin {aligned}|\Gamma ( a + b i ) |^ { 2 } & = |\Gamma (a)| ^ { 2 } \prod _ { k = 0 } ^ { \infty } { \frac { 1 } { 1 +{\frac { b ^ { 2 } } { ( a + k ) ^ { 2} } } } } \\[4pt]|\Gamma (bi)| ^ { 2 } & = { \frac {\pi }{b\sinh ( \pi b ) } } \\[6pt]| \Gamma \left ( { \tfrac { 1 }{ 2 } } + b i \right ) | ^ { 2 } & = { \frac { \pi } { \cosh ( \pi b ) } } \end{aligned} } } $$

مشهورترین مقدار گاما به ازای مقادیر غیر طبیعی، مقدار $$ \Gamma ( \frac { 1 } { 2 } ) $$ است. این مقدار برابر است با:

$$ {\displaystyle \Gamma \left ( { \tfrac { 1 } { 2 } } \right ) = { \sqrt { \pi } } } $$

مقدار فوق را می‌توان با قرار دادن $$ { \displaystyle z = { \frac { 1 } { 2 } } } $$ در معادله بازتابی یا تکراری بدست آورد. البته با تغییر متغیر $$ { \displaystyle u = { \sqrt { x } } } $$ و قرار دادن آن در انتگرال نیز به همین مقدار دست یافت. با استفاده از این مقدار می‌توان گامای تمامی مقادیر با مقدار غیرصحیح $$ \frac { 1 } { 2 } $$ را با استفاده از یکی از دو رابطه زیر بدست آورد.

$$ { \displaystyle { \begin {aligned} \Gamma \left ( { \tfrac { 1 }{ 2 } } + n \right ) & = {(2n)! \over 4 ^ { n }n ! } {\sqrt {\pi }}={\frac {(2n-1 ) ! ! } { 2 ^ { n} } } { \sqrt {\pi } } = { n - { \frac {1}{2}} \choose n}n!{\sqrt {\pi }}\\[8pt]\Gamma \left({\tfrac { 1 } { 2 } } - n \right ) & = { ( - 4 ) ^{ n } n ! \over (2n)!}{\sqrt {\pi } } = { \frac { ( - 2 ) ^ { n } }{ ( 2n - 1 )! ! } } { \sqrt {\pi } } = { \frac { \sqrt {\pi } } { { - {\frac {1}{2}} \choose n } n ! } } \end{aligned} } } $$

توجه داشته باشید که در روابط فوق $$ ! ! $$ نشان‌دهنده فاکتوریل دوبل بوده و به ازای $$ n = 0 $$، مقدار $$ {\displaystyle n!!=1} $$ برقرار است.

بیان‌ها و کاربرد‌ها

فرمول‌های زیادی از انتگرال نوع دوم وجود دارد که می‌توان با استفاده از آن‌ها تابع گاما را توضیح داد. در ابتدا باید بگوییم که در ریاضیات دو نوع انتگرال اویلر وجود دارد که در زیر آمده‌اند.

$$ { \mathrm { \mathrm { B } } } ( x , y ) = \int _ { 0 } ^ { 1 }t ^ { { x - 1 } } (1 -t ) ^ { { y - 1 } } \, d t = { \frac { \Gamma ( x ) \Gamma ( y ) } { \Gamma ( x + y) } } $$
انتگرال نوع اول

انتگرال نوع اول بیان‌کننده تابعی تحت عنوان تابع گاما است که در مطلبی مجزا این تابع را توضیح خواهیم داد. انتگرال نوع دوم نیز همان تابع گاما است که در زیر ارائه شده است.

$$ { \displaystyle \Gamma ( z ) = \int _ { 0 } ^ { \infty } t ^ { z -1 } \, e ^ { - t } \, d t } $$
انتگرال نوع دوم

البته این رابطه به ازای مقادیر طبیعی و مثبت $$ m , n $$، مطابق با رابطه زیر تعریف می‌شود.

$$ { \displaystyle \mathrm {\mathrm {B} } ( n , m ) = { ( n - 1) ! ( m - 1 ) ! \over ( n + m - 1 ) ! } = { n + m \over n m { n + m \choose n } } } $$

زمانی که بخش حقیقی عدد $$ z $$ مثبت باشد، می‌توان تابع گاما را به‌صورت زیر بیان کرد:

$$ { \displaystyle \Gamma ( z ) = \int _ { 0 } ^ { 1 } \left ( \log { \frac { 1 } { t } } \right ) ^ { z - 1 } \, d t } $$

رابطه انتگرالی اولِ ارائه شده توسط Binet نیز بیان می‌کند که در صورت مثبت بودن بخش حقیقی $$ z $$، می‌توان رابطه زیر را برای لگاریتم تابع گاما بیان کرد:

$$ { \displaystyle \log \Gamma ( z ) = \left ( z - { \frac { 1 }{ 2 } } \right ) \log z - z + { \frac { 1 } { 2 } } \log ( 2 \pi ) + \int _ { 0 } ^ { \infty } \left ( { \frac { 1 } { 2 } } - { \frac { 1 } { t } } + { \frac { 1 }{ e ^ { t} - 1 } } \right ) { \frac { e ^ { - t z } } { t } } \, d t . } $$

البته انتگرال قرار گرفته در سمت راست معادله را می‌توان در قالب تبدیل لاپلاس به‌صورت زیر بیان کرد:

$$ { \displaystyle \log \left ( \Gamma ( z ) \left ( { \frac { e } { z } } \right ) ^ { z } { \sqrt { 2 \pi z } } \right ) = { \mathcal { L } } \left ( { \frac { 1 } { 2 t } } - { \frac { 1 } { t ^ { 2 } } } + { \frac { 1 }{ t (e ^ {t } - 1 ) } } \right ) ( z ) } $$

فرمول انتگرالی Binet را می‌توان دوباره و در حالتی بیان کرد که مقدار حقیقی $$ z $$ مثبت باشد. در این شرایط، لگاریتم گامای یک عدد مختلط را می‌توان به‌صورت زیر بیان کرد:

$$ { \displaystyle \log \Gamma ( z ) = \left ( z - { \frac { 1 } { 2 } } \right ) \log z - z + { \frac‌ { 1 } { 2 } } \log ( 2 \pi ) + 2 \int _ { 0 } ^ { \infty } { \frac { \arctan ( t / z ) } { e‌ ^ { 2 \pi t } - 1 } } \, d t‌ } $$

بسط فوریه تابع گاما

بسط فوریه لگاریتم تابع گاما را می‌توان در بازه $$ { \displaystyle 0 < z < 1 } $$ مطابق با رابطه زیر بیان کرد:

$$ { \displaystyle \ln \Gamma (z)=\left({\frac { 1 } { 2 } } - z \right ) ( \gamma + \ln 2 ) + ( 1 - z ) \ln \pi - { \frac { 1 } { 2 } } \ln \sin(\pi z ) + { \frac { 1 } { \pi } } \sum _ { n = 1 } ^ { \infty } { \frac { \ln n}{ n } } \sin ( 2 \pi n z ) } $$

برای مدت‌های بسیاری تصور می‌شد که این فرمول توسط ارنست «ادوارد کومر» (Ernst Kummer) ریاضیدان آلمانی ارائه شده است. در حقیقت این فرمول توسط دو ریاضیدان به نام‌های «Iaroslav Blagouchine» و «Carl Johan Malmsten» در سال ۱۸۴۲ اثبات شده است.

فرمول رابه

در سال ۱۸۴۰ «جوزف رابه» (Joseph Raabe) فرمول زیر را به ازای مقادیر مثبت $$ a $$ اثبات کرد.

$$ { \displaystyle \int _ { a }^ { a + 1 } \ln \Gamma ( z ) \, d z ={ \tfrac { 1 } { 2 } } \ln 2 \pi + a \ln a - a ,\quad a > 0 } $$

در حالتی خاص که $$ a = 0 $$ است، رابطه فوق به‌صورت زیر در می‌‌آید.

$$ { \displaystyle \int _ { 0 } ^ { 1 } \ln \Gamma ( z ) \, d z = { \tfrac { 1 } { 2 } } \ln 2 \pi } $$

تابع پی

نمادگذاری دیگری که توسط گاوس، به منظور معرفی تابع گاما استفاده شد، به‌صورت زیر بود. این نماد همان پی بزرگ یا $$ \Pi $$ است. در حقیقت تابع اولیه پی مطابق با رابطه زیر تعریف می‌شود.

$$ { \displaystyle \Pi ( z ) = \Gamma ( z + 1 ) = z \Gamma ( z ) = \int _ { 0 } ^ { \infty } e ^ { - t } t ^ { z } \, d t } $$

در نتیجه به ازای هر مقدار غیرمنفی $$ n $$ می‌توان عبارت زیر را بیان کرد:

$$ { \displaystyle \Pi ( n ) = n ! } $$

طبق این تعریف و با استفاده از فرمول بازتابی بیان شده در بالا می‌توان حاصل ضرب تابع پی برای دو مقدار قرینه از $$ z $$ را مطابق با رابطه زیر توصیف کرد.

$$ { \displaystyle \Pi ( z ) \Pi ( - z ) = { \frac { \pi z } { \sin ( \pi z ) } } = { \frac { 1 } { \operatorname { sinc } ( z ) } } } $$

در رابطه فوق $$ sinc $$ نشان‌دهنده میانگین است. هم‌چنین با استفاده از قضیه ضرب، می‌توان رابطه زیر را بیان کرد:

$$ { \displaystyle \Pi \left ( { \frac { z } { m } } \right ) \, \Pi \left ( { \frac { z - 1 } { m } } \right ) \cdots \Pi \left ( { \frac { z - m + 1 } { m } } \right ) = ( 2 \pi ) ^ { \frac { m - 1 } { 2 } } m ^ { - z - { \frac { 1 } { 2 } } } \Pi ( z ) } $$

البته در برخی موارد، عکس تابع تعریف شده در بالا را نیز به‌صورت زیر بیان می‌کنند.

$$ \pi ( z ) = { \frac { 1 } { \Pi ( z ) } } $$

تابع لگاریتم-گاما

با توجه به این‌که هر دو تابع گاما و فاکتوریل با سرعت بالایی رشد می‌کنند، بنابراین بسیاری از ابزار‌های محاسباتی توابعی دارند که مقادیر گاما را به‌صورت لگاریتم به عنوان خروجی تحویل می‌دهد. معمولا در ابزار‌های محاسباتی همچون ماشین‌حساب این عملگر با عناوینی همچون $$ \boxed { \text {lgamma}} $$ یا $$ \boxed { \text {lngamma}} $$ مشخص شده است. در اکثر موارد برای ترکیب کردن لگاریتم و تابع گاما از عبارتی به‌صورت زیر استفاده می‌شود.

$$ { \displaystyle \ln \Gamma ( z ) = - \gamma z - \ln z + \sum _ { k = 1 } ^ { \infty } \left[ { \frac { z } { k } } - \ln \left ( 1 + { \frac { z } { k } } \right ) \right] } $$

می‌توان گفت نسخه لگاریتمی تابع گاما در فیزیک امواج کاربرد بسیاری دارد. از این همواره تلاش بر این بوده که در مقادیری خاص از $$ z $$، تقریبی برای این تابع ارائه شود. برای نمونه به ازای مقادیر حقیقی بزرگِ $$ z $$، گاوس تقریب زیر را پیشنهاد می‌دهد.

$$ { \displaystyle \ln \Gamma ( z ) \approx ( z - { \tfrac { 1 } { 2 } } ) \ln z - z + { \tfrac { 1 } { 2 } } \ln ( 2 \pi ) } $$

هم‌چنین با استفاده از رابطه ارائه شده توسط Böhmer در سال ۱۹۳۹، می‌توان به ازای مقادیر به نسبت کوچک‌ترِ $$ R e ( z ) $$ نیز از تقریب زیر استفاده کرد.

$$ { \displaystyle \ln \Gamma ( z - m ) = \ln \Gamma ( z ) - \sum _ { k =1 } ^ { m } \ln ( z - k ) . } $$

البته با استفاده از تقریب استرلینگ می‌توان عبارت دقیق‌تر زیر را نیز بدست آورد.

$$ { \displaystyle \Gamma ( z ) \sim z ^ { z - { \frac { 1 } { 2} } } e ^ { - z } { \sqrt { 2 \pi } } \left ( 1 + { \frac { 1 } {12 z } } + { \frac { 1 }{ 288 z ^ {2 } } } -{ \frac {139}{51\,840z^{3}}}-{\frac {571}{2\,488\,320 z ^ { 4 } } } \right ) } $$

همان‌طور که مشاهده می‌کنید در تقریب فوق از تعداد بیشتری از جملات بسط مجانبیِ $$ \ln ( Γ ( z ) ) $$ استفاده شده است. تابع گاما در بسیاری از مباحث ریاضی و فیزیک کاربرد دارد و در مطالب آینده به تعدادی از این کاربرد‌ها اشاره خواهیم کرد.