اندازه اثر و محاسبه آن – راهنمای کاربردی
در آزمون فرض آماری، معنیداری (Statistical Significance) به طور خلاصه، احتمال مشاهده نمونه تصادفی با توجه به صحیح بودن یک فرض آماری است. اگر این احتمال ضعیف باشد، به نظر میرسد که فرض مورد نظر در آزمون، صحیح نخواهد بود. البته این موضوع را هم باید در نظر گرفت که هدف از انجام آزمون فرض، نشان دادن مطابقت (یا عدم مطابقت) دادهها با توجه به فرضیههای آماری است. اندازه اثر (Effect Size) میزان این انطباق را به صورت یک مقدار عددی نشان میدهد که درک آن نیز به سادگی صورت میگیرد. به همین جهت این مطلب را اختصاص به اندازه اثر و محاسبه آن قرار دادهایم تا در تحلیلهای آماری، به کمک آن، نتیجه قابل درکی از آزمونهای آماری حاصل کنیم. در این بین برای انجام محاسبات و بدست آوردن مقادیر فرمولها از نرمافزارهای محاسباتی مختلف (مثلا ترکیبی از SPSS و اکسل) به عنوان یک ابزار کمک گرفتهایم و به کمک نمودارهای ترسیم شده نیز اندازه اثر را ترسیم و حجم نمونه و توان آزمونها را با هم مقایسه خواهیم کرد.


برای آشنایی بیشتر با مباحث مربوط به این نوشتار، بهتر است به عنوان مقدمه، مطالب دیگر مجله فرادرس با عنوانهای استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات و مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری را مطالعه کنید. همچنین مطالعه نوشتارهای آزمون فرض میانگین جامعه در آمار — به زبان ساده و رگرسیون خطی — مفهوم و محاسبات به زبان ساده نیز خالی از لطف نیست.
اندازه اثر و محاسبه آن
همانطور که گفته شد، «اندازه اثر» (Effect Size) یک مقدار عددی است که تفاوت بین دادهها و فرضیه آماری را مشخص و تعیین میکند. در این نوشتار به بررسی اندازه اثر برای چند آزمون و روش آماری میپردازیم که در ادامه فهرست شدهاند.
- آزمونهای کای ۲ (Chi Square Tests)
- آزمونهای تی ( T-tests)
- همبستگی پیرسون (Pearson Correlations)
- تحلیل واریانس (ANOVA)
- رگرسیون خطی (Linear Regression)
- اندازه اثر ابزاری برای تعیین اثرات درون و بین آزمودنیها (Within and between Subjects) است.
- برای محاسبه توان () در آزمونهای آماری احتیاج به محاسبه اندازه اثر داریم. این مقدار به واسطه محاسبه احتمال رد یک فرضیه برحسب فرض مقابل تعیین میشود.
- اندازه اثر برای تعین حجم نمونه موثر است. به این ترتیب به کمک آن توان آزمونها را میتوان افزایش داد. البته مشخص است که هر چه تعداد نمونهها بیشتر باشد، توان آزمون نیز افزایش خواهد یافت.
بسیاری از نرمافزارهای محاسبات آماری، قادر هستند برای بعضی از آزمونهای آماری، اندازه اثر را محاسبه و طبق جدول شماره ۱، گزارش دهند. کران و میزانهای با اهمیت بودن مقدار اندازه اثر برای هر یک از آزمونها نیز در این جدول دیده میشود.
جدول ۱: کرانهای اندازههای اثر مختلف در آزمون و تحلیلهای آماری مختلف
| ردیف | نام تحلیل | شرح | نام اندازه اثر | اثر ضعیف | اثر متوسط | اثر زیاد |
| ۱ | Chi-Square Independence Test | تحلیل کای ۲ و آزمون استقلال | Cohen's W | 0.1 | 0.3 | 0.5 |
| ۲ | Chi-Square Independence Test | تحلیل کای ۲ و آزمون استقلال | Contingency Coefficient | 0.1 | 0.29 | 0.45 |
| ۳ | Chi-Square Independence Test | تحلیل کای ۲ و آزمون استقلال | Cramér's V | - | - | - |
| 4 | Chi-Square Goodness-of-Fit Test | آزمون کای ۲ برای برازش توزیع | Cohen's W | 0.1 | 0.3 | 0.5 |
| 5 | Independent Samples T-Test | آزمون نمونهای تی | Cohen's D | 0.2 | 0.5 | 0.8 |
| 6 | Independent Samples T-Test | آزمون نمونهای تی | Rpb - Point-Biserial Correlation | 0.1 | 0.24 | 0.37 |
| 7 | Paired Samples T-Test | آزمون نمونهای تی روجی | Cohen's D | 0.2 | 0.5 | 0.8 |
| 8 | One-Sample T-Test | آزمون نمونهای تی تکی | Cohen's D | 0.2 | 0.5 | 0.8 |
| 9 | Pearson Correlation | ضریب همبستگی پیرسون | R - Correlation | 0.1 | 0.3 | 0.5 |
| 10 | ANOVA | تحلیل واریانس | ω² - Omega Squared | 0.01 | 0.06 | 0.14 |
| 11 | ANOVA | تحلیل واریانس | η² - (Partial) Eta Squared | 0.01 | 0.06 | 0.14 |
| 12 | ANOVA | تحلیل واریانس | Cohen's F | 0.1 | 0.25 | 0.4 |
| 13 | Linear Regression - Entire Model | مدل کامل رگرسیون خطی | Model R² - R Squared | 0.02 | 0.13 | 0.26 |
| 14 | Linear Regression - Entire Model | مدل کامل رگرسیون خطی | Model F² - F Squared | 0.02 | 0.15 | 0.35 |
| 15 | Linear Regression - Individual Predictor | برای هر متغیر در مدل رگرسیون خطی | Predictor R²sp - Squared Semipartial ("Part") Correlation | 0.02 | 0.13 | 0.26 |
| 16 | Linear Regression - Individual Predictor | برای هر متغیر در مدل رگرسیون خطی | Predictor F² - F Squared | 0.02 | 0.15 | 0.35 |
در ادامه هر یک از این اندازه اثرها را مرور و بررسی خواهیم کرد. البته بسیاری از این اندازهها توسط نرمافزار آماری SPSS یا محیط برنامهنویسی پایتون، نیز قابل محاسبه است.
اندازه اثر در آزمونهای کای ۲
زمانی که با یک جدول توافقی (Contingency Table) کار میکنید میتوانید استقلال یا وابستگی دو متغیر طبقهای را مورد آزمون قرار دهید. در این بین شیوههای مختلفی برای اندازهگیری میزان اثر وجود دارد. برای مثال محاسبه اندازه اثر برای زمانی که آزمون استقلال یا برازش توزیع در جدول توافقی صورت میگیرد توسط شاخص یا اندازه اثر W کوهن بدست میآید.
اندازه اثر در آزمونهای کای ۲ برای استقلال
اندازه اثر کوهن (Cohen's W Effect Size) در جدول توافقی که با علامت نیز نشان داده میشود، مطابق با رابطه زیر بدست میآید.
در رابطه بالا، پارامترها، به صورت زیر هستند.
- تعداد سلولهای جدول توافقی را نشان میدهد.
- درصد مشاهدات در هر خانه از جدول را مشخص میکند.
- درصد مورد انتظار در هر خانه از جدول برحسب فرض صفر را مشخص میکند.
کرانهای مورد نظر برای نمایش میزان اثر طبق آماره یا اندازه اثر بر اساس جدول ۱ تعیین خواهد شد. برای مثال اگر اندازه اثر بزرگتر از 0.5 باشد، نشانگر میزان اثر زیاد در نمونه تصادفی و آزمون استقلال یا برازش توزیع است.
البته با استفاده از دو شیوه دیگر نیز میتوان را محاسبه کرد. رابطه زیر نحوه محاسبه اندازه اثر را برحسب ضریب توافق (Contingency Coefficient) را نشان میدهد. در این رابطه بیانگر ضریب توافق در جدول توافقی است. برای مشاهده نحوه محاسبه بعضی از شاخصهای توافق بهتر است نوشتار جدول توافقی و کاربردهای آن در SPSS — از صفر تا صد را نیز مطالعه کنید.
شیوه دیگر برای محاسبه اندازه اثر در آزمونها مبتنی بر جدول توافقی، بهرهگیری از ضریب کرامر است که به آن «وی کرامر» (Cramer's V) نیز گفته میشود. در ادامه نحوه این ارتباط به خوبی مشخص شده است.
در این رابطه کوچکترین مقدار طول یا عرض جدول توافقی است. به این معنی که هر بعدی از جدول توافقی که کوچکتر باشد، به عنوان مقدار قرار میگیرد.
نکته: در اکثر برنامه یا بستههای محاسبات آماری مانند SPSS، اندازه اثر به طور خودکار محاسبه نمیشود ولی برای بدست آوردن آن میتوانید ضرایب گفته شده در جدول توافقی را بوسیله SPSS استخراج کرده، به شکل دستی، اندازه اثر را بدست آورید.
اندازه اثر در آزمونهای کای ۲ برای برازش توزیع
یکی از روشهای برازش توزیع (Goodness of Fit Test)، به کارگیری آزمون کای ۲ است. البته به این منظور ابزارهای مختلفی در نرمافزارهای محاسبات آماری مانند SPSS وجود دارد.
توان آزمون اندازه نمونه برای آزمون کای ۲ در این حالت به طور مستقیم برحسب اندازه اثر قابل محاسبه نیست. این مقادیر با توجه به وابستگی توزیع کای ۲ به درجه آزادی (Degree of Freedom) تغییر میکند.
نموداری که در زیر مشاهده میکنید، اندازه اثر (Effect size W)، تعداد حجم نمونه (Total Sample Size) را برای آزمون برازش توزیع و توان آزمون آن (Power) یا همان در جدول توافقی نشان میدهد. محور افقی در اینجا توان آزمون و محور عمودی نیز حجم نمونه را نشان میدهد، خطوط رنگی نیز اندازه اثر را با توجه به جدول ۱، مشخص کرده است.
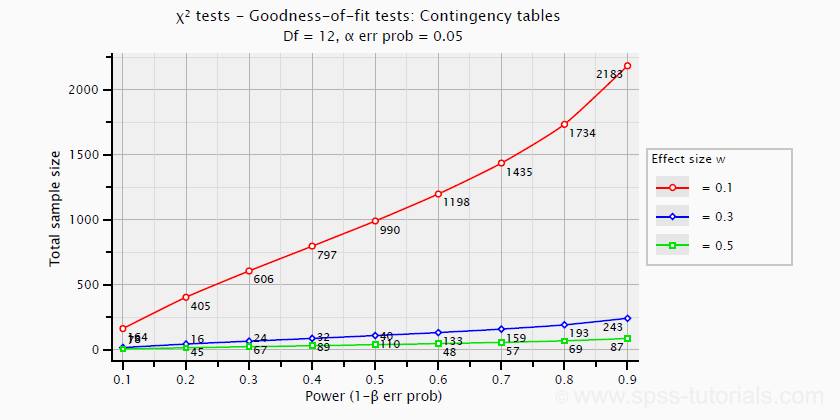
واضح است که در اینجا احتمال خطای نوع اول و درجه آزادی نیز برابر با ۱۲ است که حاصلضرب است. در نتیجه جدول توافقی شامل ۵ سطر و ۴ ستون است.
اندازه اثر آزمونهای تی (T Tests)
اندازه اثر برای آزمون تی را در دو رویکرد میتوان محاسبه کرد. برای هر نوع آزمون تی، آماره کوهن D قابل استفاده است. البته در زمانی که آزمون برای نمونههای مستقل صورت میگیرد، استفاده از ضریب همبستگی سریالی نقطهای (point-biserial correlation) نیز قابل استفاده خواهد بود.
آزمون تی تک نمونهای یا نمونههای مستقل (Independent Sample T test)
در نوشتارهای دیگر مجله فرادرس با آزمون تی برای مقایسه میانگین گروهها مستقل آشنا شدهاید. به یاد دارید که آماره آزمون برای مقایسه میانگین دو جامعه مستقل به شکل زیر محاسبه میشود.
که در آن میانگین اول و ، میانگین جامعه دوم و نیز انحراف معیار حاصل از جذر واریانس ترکیبی (Pooled Variance) دو جامعه است. به این ترتیب مقدار اندازه اثر کوهن خواهد بود.
آزمون تی زوجی (Paired Sample T test)
در آزمون تی زوجی در حقیقت با یک آزمون تک نمونهای مواجه هستیم که مقادیر متغیر، براساس تفاضل مقادیر زوجها حاصل شده و میانگین این تفاضلها را با مقدار میانگین فرض یا دلخواه () مقایسه میکنیم.
آماره این آزمون نیز به شکل زیر خواهد بود.
واضح است که در این رابطه، میانگین حاصل از تقاضل زوجها و نیز انحراف معیار این مقادیر بوده و به عنوان برآورد انحراف معیار جامعه به کار میرود. در این حالت نیز اندازه اثر کوهن نامیده میشود.
همچنین نیز مقدار حدسی یا اختیاری است که در فرض صفر لحاظ یا در نظر گرفته شده. از آنجایی که باز هم اندازه اثر به درجه آزادی و سطح آزمون () بستگی دارد، نمودار زیر را برای تعیین اندازه اثر برحسب این پارامترها ترسیم کردهایم.
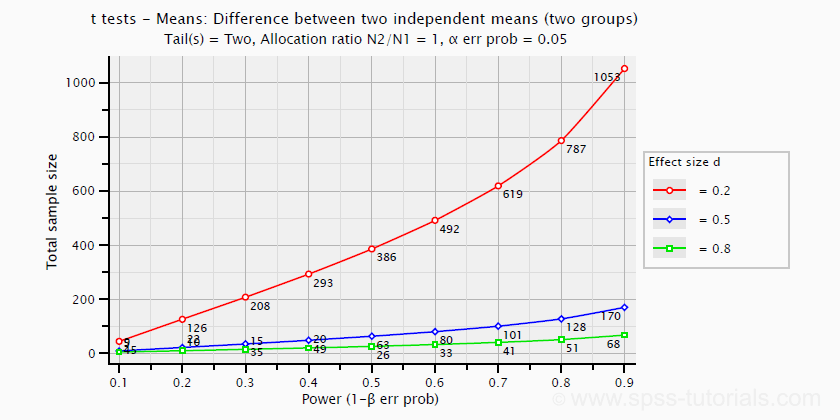
توسط این نمودار مشخص میشود که توان و حجم نمونه مناسب برای انجام آزمون برای مشخص کردن اندازه اثر چقدر خواهد بود. محورها و مقادیر آنها درست به مانند نمودار قبلی تعیین و مشخص شده است. مبنای محاسبه اندازه اثر نیز همان مقدار کوهن D محسوب شده است.
نکته: برای تعیین شدت اندازه اثر، مطابق با جدول ۱، تفسیر یا گزارش آماری ارائه میشود.
ضریب همبستگی پیرسون
ضریب «همبستگی پیرسون» (Pearson Correlation) به عنوان ابزار یا ملاکی برای نمایش میزان شدت رابطه خطی بین دو متغیر تصادفی یا مقادیرشان مورد محاسبه قرار میگیرد.
هر چه شدت رابطه خطی بین دو متغیر بیشتر باشد، کوواریانس (Covariance) بین آنها بزرگتر شده، در نتیجه ضریب همبستگی پیرسون بزرگتر خواهد بود. در صورتی که مقدار ضریب همبستگی برابر با ۱ یا ۱- باشد، بیشتری شدت یا رابطه دقیق خطی بین دو متغیر برقرار است.
محاسبه ضریب همبستگی توسط همه نرمافزارهای محاسبات آماری صورت میگیرد. نحوه محاسبه ضریب همبستگی پیرسون مطابق با رابطه زیر است.
در نمودار زیر رابطه بین مقدار توان آزمون و اندازه نمونه را با توجه به اندازه خطای نوع اول () ثابت و فرض صفر که عدم رابطه خطی را مشخص میکند () مشاهده میشود. توجه دارید که در اینجا همبستگی پیرسون بین دو متغیر تصادفی در جامعه آماری است و برآورد آن توسط نمونه تصادفی محسوب میشود.
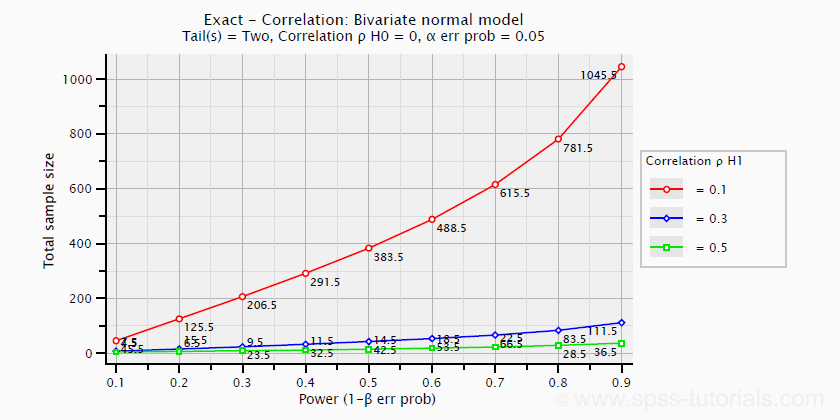
برای بررسی میزان اثر برای ضریب همبستگی از قواعد زیر پیروی کنید.
- اثر کم: زمانی که .
- اثر متوسط: زمانی که
- اثر زیاد: زمانی که .
تحلیل واریانس (ANOVA)
تحلیل واریانس (Analysis of Variance) یکی از تکنیکهای محبوب آماری است که هم برای آزمون فرض میانگین و هم برای سنجش کارایی مدل رگرسیونی به کار میرود. اندازه اثر در تحلیل واریانس به شیوههای مختلف مانند مقدار مربع اتا (Eta Squared)، اندازه کوهن F و مربع امگا (Omega Squared) قابل محاسبه است. در ادامه این متن به این شیوهها اشاره خواهیم کرد.
اندازه اثر مربع اتا (جزئی) در تحلیل واریانس
«مربع اتای جزئی» (Partial Eta Squared)، یکی از معیارهای مربوط به اندازهگیری اثر بخصوص در جدول تحلیل واریانس و شیوه استنباطی آن است. از این مقدار برای تحلیل واریانس بین آزمودنی یا «تحلیل واریانس یک طرفه» (One-way ANOVA) یا «تحلیل فاکتوریل» (Factorial ANOVA) استفاده میشود. همچنین بهرهگیری از این شاخص در «تحلیل واریانس آمیخته» (mixed ANOVA) نیز میسر است.
نحوه محاسبه اتای جزئی براساس مدل تحلیل واریانس به صورت زیر صورت میگیرد.
در رابطه بالا، مجموع مربعات تیمار یا متغیر عامل است و نیز مجموع مربعات خطا را مشخص میکند. این رابطه برای «تحلیل واریانس یک طرفه» (One-way ANOVA) همان مربع اتا را مشخص میکند. به این معنی که در این حالت، مربع اتای جزئی و مربع اتا، با یکدیگر برابر هستند.
حدود مورد نظر برای به صورت زیر تفسیر میشود.
- اثر کم: زمانی که مقدار اتا حدود باشد.
- اثر متوسط: زمانی که مقدار اتا حدود باشد.
- اثر زیاد: زمانی که مقدار اتا حدود باشد.
نکته: مقدار مربع اتا در تحلیل واریانس توسط نرمافزارهای آماری بخصوص SPSS قابل محاسبه است. برای مشاهده نحوه محاسبه آن در تحلیل کوواریانس بهتر است نوشتار تحلیل کوواریانس ANCOVA در SPSS — راهنمای کاربردی را مطالعه کنید. همچنین در مجله فرادرس، مطلب تحلیل واریانس یک طرفه در پایتون — راهنمای گام به گام و تحلیل واریانس دو طرفه در پایتون — راهنمای گام به گام نیز به این موضوع پرداختهاند.
اندازه اثر کوهن F در تحلیل واریانس
از اندازه اثر کوهن F در تحلیلهای واریانس بین آزمودنی و تحلیل واریانس یک طرفه و همچنین طرح فاکتوریل استفاده میشود. همچنین به کارگیری آن برای نمایش اندازه اثر در آنالیز یا تحلیل واریانس با مقادیر تکراری یا تحلیل واریانس آمیخته، مشکلی نخواهد داشت.
نحوه محاسبه اثر کوهن F مطابق با رابطه زیر است. توجه داشته باشید که به این ترتیب، ارتباطی بین اندازه اثر مربع اتا یا «اتا جزئی» (Partial eta-squared) و اندازه اثر کوهن F بوجود خواهد آمد.
تفسیر مقدار نیز به شکل زیر صورت میگیرد.
- اثر کم: مقدار یا حدود آن.
- اثر متوسط: مقدار یا حدود آن.
- اثر زیاد: مقدار یا حدود آن.
تعیین تعداد یا حجم نمونه و توان آزمون مربوط به تحلیل واریانس را میتوان براساس اثر کوهن F نیز محاسبه کرد. در تصویر زیر، رابطه بین این سه عامل را میتوان مشاهده کرد. البته توجه داشته باشید که تعداد گروهها در تحلیل واریانس یک طرفه، یا «اثرات ثابت» (Fixed Effects) برابر با ۳ و احتمال خطای نوع اول نیز محسوب شده است.
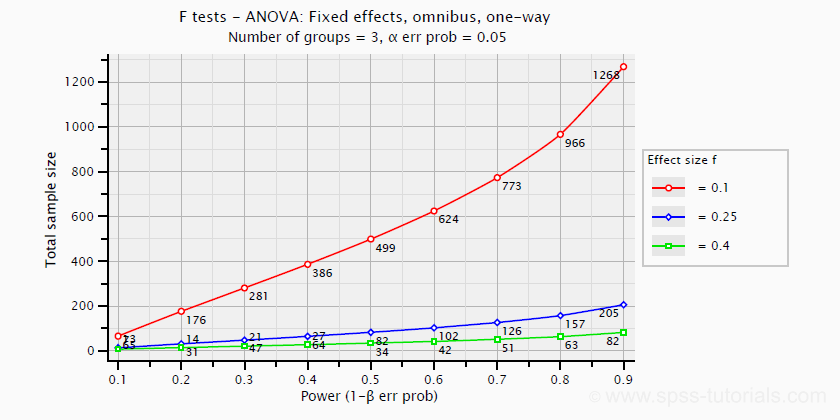
اندازه اثر امگا در تحلیل واریانس
یکی دیگر از شاخصهای اندازه اثر که کمتر مورد استفاده قرار میگیرد، مربع امگا (Omega Squared) است که با نماد شناخته میشود.
اگر ، مجموع مربعات تفاضل مقادیر از میانگین کل، و به ترتیب، مجموع مربعات خطای تیمارها و درجه آزادی مربوطه باشند و همچنین نیز میانگین مربعات خطای تیمار نشان دهد، نحوه محاسبه به شکل زیر خواهد بود.
مقداری که مربع امگا () مشخص میکند، درست به مانند مربع اتا ()، درصدی از واریانس است که توسط متغیر عامل توجیه یا بیان میشود. به نظر میرسد که امگا، دارای «اریبی» (Biased) کمتری نسبت به اتای برای برآورد واریانس کل جامعه است.
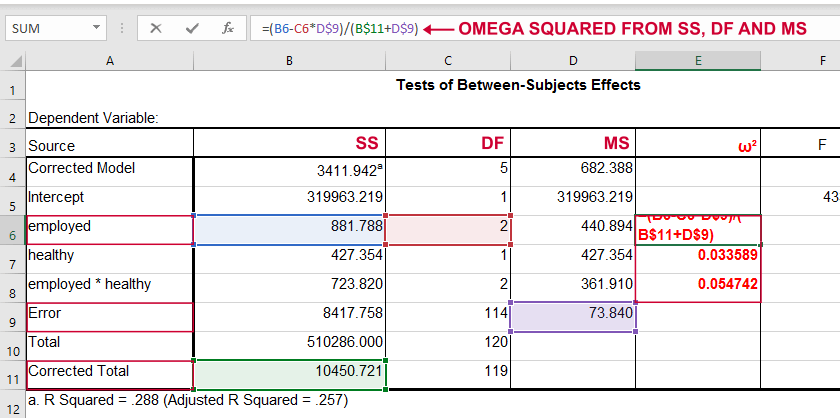
تصویر ۵، که توسط اکسل تولید شده است، نحوه محاسبه امگا از خروجی SPSS در تحلیل واریانس دوطرفه بوده که با توجه به رابطه بالا محاسبه شده است.
رگرسیون خطی و اندازه اثر
روشها یا شیوههای اندازهگیری اثر در مدل رگرسیون خطی ساده یا چندگانه (Simple and Multiple Linear Regression) متفاوت است. برای مثال ضریب تعیین یا ضریب تعیین جزئی و آماره برای اندازه اثر در مدل رگرسیونی مورد استفاده هستند.
خصوصیات و شرایط استفاده از هر یک از آنها را به صورت فهرست زیر مشاهده میکنید.
- برای محاسبه اندازه اثر برای کل مدل رگرسیونی و تک تک متغیرها قابل استفاده است.
- برای نمایش اندازه اثر برای مدل کلی رگرسیونی محاسبه میشود که در آن همه متغیرهای مستقل حضور دارند.
- که ضریب تعیین جزئی برای تک تک متغیرهای موجود در مدل قابل محاسبه بوده و اثر هر یک از آنها را روی متغیر پاسخ تعیین میکند.
اندازه اثر F در رگرسیون خطی
همانطور که گفته شد، یکی از روشهای محاسبه اندازه اثر در مدل رگرسیون خطی (ساده و چندگانه) است. نحوه محاسبه این شاخص به صورت زیر است:
توجه داشته باشید که در رابطه بالا، منظور از میزان افزایش مقدار ضریب تعیین () در زمانی است که یک سری از متغیرهای مستقل به مدل اضافه میشوند. بنابراین میتوان مقدار آن را برای تک تک متغیرهای مستقل محاسبه کرد. به این معنی که میزان افزایش ضریب تعیین را با توجه به حضور و عدم حضور آن متغیر اندازهگیری کرده و سپس مقدار را بدست آورد. به این ترتیب میزان اثر متغیر مورد نظر در مدل رگرسیونی حاصل میشود.
فرض کنید متغیر در مدل رگرسیونی حضور داشته و مقدار محاسبه شده است. حال متغیر بعدی را به مدل اضافه میکنیم و مقدار ضریب تعیین را با حضور این متغیر در مدل بدست میآوریم. تفاضل این دو مقدار که ضریب همبستگی نیمه جزئی (Semipartial Correlation) نامیده و به صورت نشان داده میشود، در محاسبه اندازه اثر دخالت داده میشود.
در زمانی که مدل کامل رگرسیونی مد نظر باشد، اندازه اثر را براساس مقدار در حضور و عدم به کارگیری همه متغیرها در مدل رگرسیونی محاسبه کرده و اختلاف آنها را به عنوان در نظر میگیریم. از آنجایی که مدل رگرسیونی بدون هیچ متغیر مستقلی، فقط براساس میانگین متغیر وابسته نوشته میشود، ضریب تعیین برابر با صفر خواهد بود. بنابراین مقدار با مقدار ضریب تعیین مدل کامل رگرسیونی برابر است.
در تصویر 6، نمونه یک محاسبه اندازه اثر را براساس خروجی نرمافزار SPSS و محاسبه توسط اکسل را مشاهده میکنید.
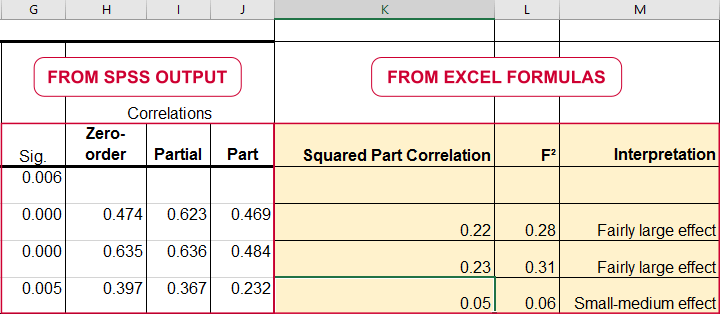
اندازه اثر برای محاسبه توان و حجم مورد نیاز در مدل رگرسیونی با توجه به متغیرهای مستقل و خطای نوع اول در آزمون مربوط به پارامترهای رگرسیونی به کار گرفته میشود. البته مشخص است که مقدار به تعداد متغیرهای مستقل در مدل نیز مرتبط است.
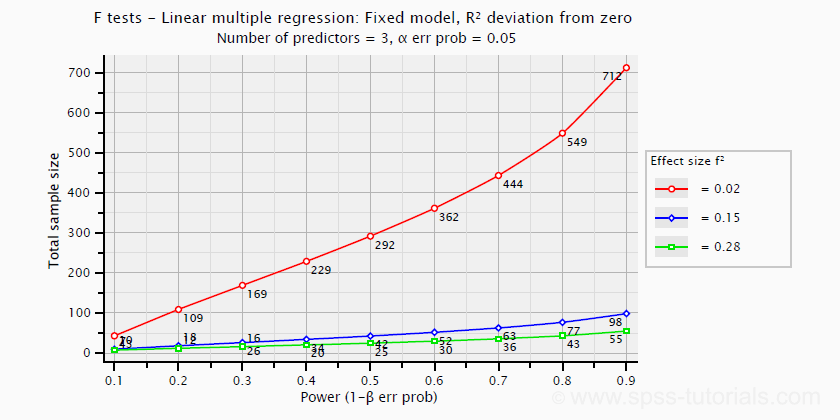
در تصویر ۷، نحوه ارتباط اندازه اثر و توان آزمون همچنین حجم نمونه برای ۳ متغیر مستقل در مدل رگرسیونی نمایش داده شده است. ارقامی که روی نمودار ظاهر شدهاند، تعداد نمونههای لازم برای رسیدن به توان آزمون مورد نظر تحت اندازه اثر است. واضح است که هر چه اندازه اثر بیشتر باشد به حجم نمونه کمتری احتیاج است.
تفاوت اندازه اثر و مقدار احتمال
ممکن است اندازه اثر با مقدار احتمال (p-Value) اشتباه گرفته شود. گاهی به اشتباه کم بودن مقدار احتمال را به عنوان ارتباط بیشتر بین متغیرها یا قدرت بیشتر در رد فرض صفر تلقی میکنند. در حالیکه مقایسه مقدار احتمال با احتمال خطای نوع اول، یک معیار برای تایید یا فرض صفر است و بزرگی یا کوچکی مقدار احتمال در آزمون فرض نقشی ندارد. زمانی فرض صفر را رد میکنیم که مقدار احتمال از احتمال خطای نوع اول () کوچکتر باشد.
به این ترتیب مقدار احتمال نشان میدهد که مثلا آیا یک عامل روی میانگین تاثیر گذار است یا خیر! در حالیکه اندازه اثر میزان تاثیر عامل را روی میانگین مشخص میکند. بنابراین میتوان اندازه اثر را ابزاری مناسبتر در تحلیل و آزمونهای آماری در نظر گرفت. همچنین به این موضوع نیز توجه داشته باشید که اندازه اثر وابسته به حجم نمونه نبوده و مستقل از آن است.
از آنجایی که اندازه اثر را میتوان ابزاری برای مقایسه تحقیقها و مطالعات آماری در نظر گرفت، امروزه در فرا-تحلیلها (Meta-Analysis) به کار برده میشود در حالیکه مقدار احتمال این ویژگی و خاصیت را ندارد. به همین علت در تحقیقات روانشناسی و پزشکی استفاده از اندازه اثر بسیار رواج دارد.
خلاصه و جمعبندی
در این نوشتار با مفهوم اندازه اثر در آمار و همچنین شیوه محاسبه و کاربردهای آن آشنا شدید. همانطور که دیدید، مفهوم اندازه اثر در مباحث مربوط به ازمون فرض آماری از اهمیت زیادی برخوردار است. به این ترتیب میزان تاثیر گذاری متغیرهای مستقل روی متغیر پاسخ اندازهگیری شده و نتایج آزمون فرض آماری به شکل مناسبتری توصیف و ارائه میشوند. توان آزمون و تعیین حجم نمونه از مواردی است که اندازه اثر در آن نقش دارند.
نمودارها و تصاویری که در این نوشتار ترسیم شده بودند، نشان میداد که با فرض ثابت بودن خطای نوع اول و پارامترهای دیگر توزیع آماره آزمون، حجم نمونه و اندازه اثر همچنین توان آزمون چه رابطهای با یکدیگر دارند. همچنین در انتها نیز مقایسهای بین مقدار احتمال و اندازه اثر در آزمونهای فرض آماری صورت گرفت.













با درود از مطالب مفیدی که بیان کردید.
یک سوال دارم بین Hedge’s g و Eta چه تفاوتی وجود دارد؟
سلام. وقتی مقدار اندازه اثر مثلا 4 بدست می اید تفسیر آن چیست؟ یعنی شدت اثر خیلی زیاد بوده
سلام. مطالبتون خیلی مفید بود. تشکر