تحلیل واریانس یک طرفه در پایتون — راهنمای گام به گام

تحلیل واریانس و روش‌های تجزیه و تفکیک واریانس، از دسته تکنیک‌هایی محسوب می‌شود که در روش‌های مدل‌سازی آماری اختلاف بین گروه‌ها یا دسته‌ها را بررسی و مورد تجزیه و تحلیل قرار می‌دهند. «تحلیل واریانس»‌ (Analysis of Variance) با به اختصار ANOVA، اولین بار توسط «رونالد فیشر» (R. A. Fisher) بیولوژیست و آمارشناس مشهور، برای مطالعه روی گونه‌های مختلف گیاهان ابداع و به کار گرفته شد.

او در کتاب معروف خود به نام «روش‌های آماری برای محققین» (Statistical Methods for Research Workers) روش تجزیه واریانس را معرفی و براساس آن چندین تکنیک آماری دیگر را پایه‌گذاری کرد. اساس همه این روش‌ها، تفکیک واریانس یا پراکندگی داده‌ها به چند جزء یا بخش است. امروزه کاربرد تحلیل واریانس که با این ایده انجام شده، بسیار زیاد است. در ساده‌ترین شکل، می‌توان به منظور مقایسه میانگین در بین چندین جامعه از تحلیل واریانس استفاده کرد. این کار به عنوان یک جایگزین برای آزمون فرض با استفاده از آماره آزمون T است.

همچنین بخصوص در مدل رگرسیون خطی با تجزیه واریانس کل به بخش توصیف شده توسط مدل و خطای تصادفی، جدول آنالیز واریانس تشکیل و کارایی مدل رگرسیونی مورد ارزیابی قرار می‌گیرد. در این نوشتار چهار روش تحلیل واریانس یک طرفه در پایتون را مرور کرده و به صورت گام به گام اجرا خواهیم کرد. بنابراین هر جا احتیاج به انجام محاسبات بوده، از زبان برنامه‌نویسی پایتون کمک گرفته‌ و کدهایی در این زمینه آورده‌ایم.

برای آگاهی از مفاهیم اولیه در تحلیل واریانس به مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها و برای آشنایی با روش‌های رگرسیونی به رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده مراجعه کنید. همچنین اطلاع از شیوه محاسبات مربوط به رگرسیون خطی که در مطالب رگرسیون خطی — مفهوم و محاسبات به زبان ساده و هم خطی در مدل رگرسیونی — به زبان ساده  قابل مطالعه است، خالی از لطف نیست.

تحلیل واریانس یک طرفه در پایتون

در نوشتار دیگری به نام تحلیل واریانس با داده‌های تکراری (Repeated Measure Anova Analysis) --- پیاده‌سازی در پایتون یکی دیگر از تحلیل‌های صورت گرفته توسط تفکیک واریانس معرفی شد. ولی در این نوشتار با شیوه تحلیل بین گروه‌ها توسط تحلیل واریانس آشنا شده و نحوه پیاده‌سازی آن را در پایتون با چهار روش فرا می‌گیریم. ابتدا مروری بر مباحث مربوط به تحلیل واریانس یا ANOVA خواهیم داشت، سپس با شیوه اجرای آن در پایتون آشنا خواهیم شد.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

تحلیل واریانس یک طرفه (one-way ANOVA)

تحلیل واریانس، به یک معنی مقایسه نسبت واریانس سیستماتیک و واریانس غیرسیستماتیک (تصادفی) در یک طرح آزمایشات (Experimental Design) است. مفهوم واریانس در تحلیل ANOVA نقش مهمی ایفا می‌کند و بخصوص تجزیه آن به دو بخش بین و درون گروهی (Between and Within Groups) از خصوصیات منحصر به فرد تکنیک این تحلیل محسوب می‌شود.

واریانس یا مجموع تغییرت کل را با $$SS_T$$ و واریانس یا مجموع تغییرات بین گروه‌ها یا همان تغییرات سیستماتیک را با $$SS_{between}$$ می‌شناسیم. از طرفی واریانس یا مجموع تغییرات غیرسیستماتیک یا درون گروهی نیز با $$SS_{within}$$ نشان داده می‌شود. در این صورت می‌توانیم مجموع تغییرات کل را مطابق با تصویر زیر تجزیه کنیم.

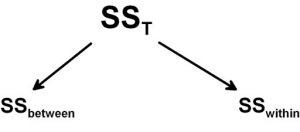
تقسیم این قسمت‌ها که از تجزیه واریانس کل ایجاد شده‌اند، به نام نسبت F نامیده می‌شود. حرف F نمایانگر حرف اول نام «فیشر» (Fisher) آماردان بزرگ است.

گاهی در  مسائل طرح آزمایشات، از اصطلاح تیمار (Treatment) برای نشان دادن گروه‌ها استفاده می‌شود. برای مثال ممکن است در بررسی میزان رشد یک گیاه، نوع آبیاری یک عامل محسوب شود که با سه سطح یا تیمار به صورت ۱- قطره‌ای، ۲- بارانی، ۳- غرق‌آبی مشخص شده است. از آنجایی که در تحلیل واریانس یک طرفه فقط یک تیمار در نظر گرفته می‌شود، آن را یکطرفه می‌نامند. به این ترتیب تیمارها نشانگر تغییرات بین گروهی خواهند بود.

از تحلیل واریانس یک طرفه (one-way ANOVA) می‌توان برای سنجش کارایی مدل رگرسیونی استفاده کرد. از طرفی می‌توان همین تکنیک را برای مقایسه میانگین بین $$k$$ جامعه آماری به کار برد. این کار درست به مانند ایجاد یک مدل رگرسیونی بوسیله یک متغیر طبقه‌ای با $$k$$ سطح یا مقدار متفاوت است. بنابراین اگر یک مدل خطی رگرسیونی را به صورت زیر براساس یک متغیر طبقه‌ای با $$j$$ سطح در نظر بگیریم، هدف برآورد پارامترها یا ضرایب مدل بوده و کارایی مدل یا صفر بودن همه ضرایب را با آزمون F که توسط نسبت یاد شده ساخته می‌شود در جدول تحلیل واریانس مشخص می‌کنیم.

$$\large y_i = b_0+b_1X_{1,i} +...+b_{j-1,i} + e_i$$

رابطه ۱

البته شاید به شیوه دیگری نیز بتوان این مدل را برای این وضعیت نمایش داد. فرض کنید که میانگین کل را با $$\mu_{grand}$$ نمایش داده‌ایم. میانگین گروه $$j$$ نیز با $$\tau_j$$ و خطای تصادفی برای مشاهده $$i$$‌ در گروه $$j$$ام را هم با $$\epsilon_{ij}$$ مشخص کرده‌ایم. به این ترتیب مدل مربوط به رابطه ۱ به صورت زیر و مطابق با رابطه ۲ نوشته خواهد شد.

$$\large y_{ij} = \mu_{grand} + \tau_j + \varepsilon_{ij}$$

رابطه ۲

به منظور انجام آزمون روی پارامترها نیاز است که داده‌ها (خطای تصادفی) دارای توزیع نرمال باشند. به این ترتیب باید هر گروه دارای توزیع نرمال خاص خود باشد تا میانگین گروه‌ها با یکدیگر تفاوت معنی‌داری داشته باشد. در این صورت توزیع آماره $$F$$ مشخص و نتایج حاصل از آزمون ANOVA قابل اطمینان خواهد بود.

البته شرط ثابت و یکسان بودن واریانس در بین هر گروه آزمودنی نیز باید برای اعتبار آزمون ANOVA وجود داشته باشد. در غیر اینصورت ممکن است نتایج حاصل از آزمون نسبت F گمراه کننده باشد. این شرط به نام یک‌شکل بودن یا «همگنی» (Homogeneity) واریانس معروف است. از طرفی متغیر وابسته یا $$Y$$ نیز باید به با مقادیری از مجموعه اعداد حقیقی و یک متغیر کمی با مقیاس نسبی (Scale) یا فاصله‌ای (Interval) باشد.

تحلیل واریانس در پایتون

در این قسمت به بررسی یک فایل اطلاعاتی در مورد رشد گیاهان می‌پردازیم که البته در زبان‌برنامه‌نویسی R موجود بوده و قابل استفاده است ولی اینجا آن را به صورت متنی ذخیره کرده و در پایتون فراخوانی می‌کنیم. برای دریافت این فایل می‌توانید با کلیک بر روی (+) فایل را دریافت کنید. در نظر بگیرید که در کد زیر، محل قرارگیری فایل اطلاعاتی در همان پوشه‌ای است که برنامه در آن قرار گرفته یا محل پیش فرض فراخوانی فایل‌ها در پایتون در نظر گرفته شده است.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

نکته: اگر فایلی که می‌خواهید در پایتون فراخوانی کنید با قالب اکسل باشد می‌توانید از تابع read_excel از کتابخانه pandas استفاده کنید. این تابع قادر به شناسایی و خواندن فایل‌هایی با قالب xlsx نیز هست.

کدی که در ادامه مشاهده می‌کنید، به منظور بارگذاری کتابخانه pandas و خواندن فایل اطلاعاتی با نام datafile نوشته شده است. منظور از متغیر group، نوع گیاه و متغیر weight‌ وزن آن را نشان می‌دهد.

1import pandas as pd
2datafile = "PlantGrowth.csv"
3data = pd.read_csv(datafile)
4 
5#Create a boxplot
6data.boxplot('weight', by='group', figsize=(12, 8))
7 
8ctrl = data['weight'][data.group == 'ctrl']
9 
10grps = pd.unique(data.group.values)
11d_data = {grp:data['weight'][data.group == grp] for grp in grps}
12 
13k = len(pd.unique(data.group))  # number of conditions
14N = len(data.values)  # conditions times participants
15n = data.groupby('group').size()[0] #Participants in each condition

البته به همراه اجرای این برنامه، نمودار جعبه‌ای (Boxplot) نیز برای مقایسه توزیع دو نوع تیمار (trt1 تا trt2) با گروه کنترل (ctrl) دیده می‌شود. این طور که به نظر می‌رسد بین میانگین توزیع این سه گروه تفاوت وجود دارد.

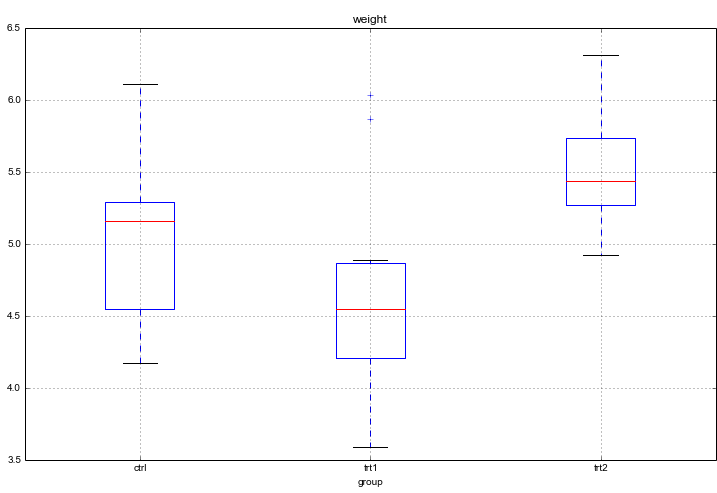
ولی اکتفا به این نمودار کار صحیحی نیست. باید این موضوع را بوسیله تحلیل واریانس نیز مورد تجزیه و بررسی قرار دهیم، زیرا ممکن است تفاوت‌ها ناشی از نمونه‌ها و نمونه‌گیری بوده و در حقیقت در جامعه آماری چنین تفاوتی وجود نداشته باشد. البته برای نمایش اختلاف یا تفاوت بین گرو‌ه‌ها یا تیمارهای حاصل از نمونه‌گیری این نمودار بسیار گویا و لازم است. اغلب بوسیله چنین نمودارهایی دست به فرضیه‌پردازی می‌زنیم و سپس با آزمون‌های آماری ادعا را مورد تجزیه و تحلیل قرار می‌دهیم. به منظور اطلاع از اصطلاحات مربوط به آزمون فرض آماری نوشتار آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات پیشنهاد می‌شود.

در ادامه به شیوه‌های مختلف اجرای تحلیل واریانس در پایتون می‌پردازیم که هر کدام دارای ویژگی‌های خاص خود هستند.

۱. استفاده از کتابخانه SciPy برای ANOVA

در این قسمت یکی از شیوه‌های تحلیل واریانس را در پایتون معرفی می‌کنیم که به کمک کتابخانه Scipy و تابع f_oneway صورت می‌گیرد. به کد زیر توجه کنید. مشخص است که پس از فراخوانی کتابخانه Scipy تابع stat.f_oneway با پارامترهایی که بیانگر گروه کنترل (ctrl) و گروه‌های تیمار (trt1) و (trt2) است، اجرا خواهد شد.

1from scipy import stats
2 
3F, p = stats.f_oneway(d_data['ctrl'], d_data['trt1'], d_data['trt2'])

درجه آزادی صورت و مخرج کسر مربوط به F احتیاج به آگاهی از تعداد پارامترها و تعداد مشاهدات دارد. درجه‌های آزادی تغییرات بین گروهی (DFbetween)، درون گروهی (DFwithin) و درجه آزادی تغییرات کل (DFtotal) در زیر مشخص شده است.

1DFbetween = k - 1
2DFwithin = N - k
3DFtotal = N - 1

واضح است که در این رابطه‌ها، k تعداد پارامترها (گروه‌ها) و N نیز تعداد مشاهدات است. از آنجایی برای محاسبه تغییرات (واریانس) کل احتیاج به برآورد میانگین کل داریم، یک واحد از درجه آزادی مربوط به تغییرات کل مشاهدات کم شده است و در نتیجه DFtotal=N-1 محاسبه شده است.

نکته: توجه داشته باشید که بین این درجه‌های آزادی باید رابطه زیر برقرار باشد.

$$\large DF_{between}+DF_{within}=DF_{total}$$

رابطه ۳

۲. استفاده از پایتون خالص در ANOVA

در حقیقت تحلیل واریانس یک طرفه، دارای محاسبات ساده‌ای است که می‌توانیم بدون استفاده از کتابخانه‌های پایتون نیز آن را اجرا کنیم. در ادامه با نحوه انجام این گونه محاسبات آشنا خواهیم شد. کافی است که مقادیر مجموع تغییرات بین گروهی (SSbetween) یا درون گروهی (SSwithin) و تغییرات کل (SStotal) را محاسبه و براساس درجه‌‌های آزادی هر یک، مقدار F را محاسبه کنیم. ابتدا به بررسی مجموع تغییرات بین گروهی می‌پردازیم.

فیلم آموزش روش تحقیق – نحوه نگارش پایان نامه در فرادرس

کلیک کنید

محاسبه مجموع مربعات تغییرات بین گروهی

مجموع تغییرات بین گروهی (Sum of Squares Between) را با SSbetween نشان می‌دهند. فرمول محاسباتی آن به صورت زیر است.

$$\large SS_{between} = \frac{\sum(\sum a_i) ^2} {n} - \frac{T^2}{N}$$

رابطه ۴

که در آن $$T^2$$‌همان مجموع مربعات تغییرات کل است.

این مقدار نشان می‌دهد میزان اشتراک گروه‌ها چقدر است. اگر مقدار SSbetween زیاد باشد، بیانگر آن است که اشتراک کمی بین گروه‌ها وجود دارد و در غیر این صورت به نظر می‌رسد که پراکندگی بین گروه‌ها کوچک بوده و می‌توان آن‌ها را یک گروه واحد در نظر گرفت. البته این کار باید با توجه به پراکندگی درون گروهی و مقایسه نسبت‌ها صورت بگیرد. فرمول یاد شده در رابطه ۴ را به صورت زیر در پایتون محاسبه می‌کنیم.

1SSbetween = (sum(data.groupby('group').sum()['weight']**2)/n) \
2    - (data['weight'].sum()**2)/N

توجه داشته باشید که در اینجا n تعداد اعضای هر گروه‌ و N نیز تعداد مشاهدات است. به این ترتیب مجموع میانگین مربعات مقدارهای هر گروه از میانگین مربعات کل مقدارها کم شده است.

محاسبه مجموع مربعات تغییرات درون گروهی

برای محاسبه مجموع مربعات تغییرات درون گروهی از فرمول یا رابطه ۵ استفاده می‌کنیم.

$$\large SS_{within} = \sum Y^2 - \frac{\sum (\sum a_i)^2}{n}$$

رابطه ۵

به منظور محاسبه این مقدار از کد زیر استفاده خواهیم کرد. مشخص است که در اینجا منظور از $$Y$$ همه مقدارها بدون در نظر گرفتن گروه است و عبارت دوم نیز میانگین هر گروه یا دسته را نشان می‌دهد. در واقع SSwithin همان مربعات فاصله بین مقدارها هر گروه با میانگین همان گروه است که به ازاء همه گروه‌ها، مجموع محاسبه شده است.

1sum_y_squared = sum([value**2 for value in data['weight'].values])
2SSwithin = sum_y_squared - sum(data.groupby('group').sum()['weight']**2)/n

محاسبه مجموع مربعات کل

با توجه به رابطه‌ای که بین مجموع مربعات کل (SStotal) با دو مجموع مربعات SSbetween و SSwithin وجود دارد، به راحتی می‌توان مقدار آن را محاسبه کرد. این رابطه به صورت رابطه ۶ نوشته می‌شود.

$$\large SS_t = \sum Y^2 - \frac{T^2}{N}$$

رابطه ۶

محاسبه این مقدار توسط پایتون در زیر آمده است.

1SStotal = sum_y_squared - (data['weight'].sum()**2)/N

نکته: البته مشخص است که مجموع مربعات تغییرات درون و بین گروهی با مجموع مربعات تغییرات کل برابر است بنابراین می‌توانستیم با جمع SSbetween و SSwithin‌ نیز SStotal را بدست آوریم.

محاسبه میانگین تغییرات و نسبت F

برای محاسبه نسبت تغییرات و بدست آوردن معیار F‌ احتیاج به میانگین تغییرات درون و بین گروه‌ها داریم. با توجه به درجه آزادی هر یک از این بخش‌ها و رابطه ۳ به راحتی می‌توان محاسبات را دنبال کرد. به این ترتیب میانگین تغییرات بین گروهی MSbetween به شکل زیر محاسبه می‌شود.

1MSbetween = SSbetween/DFbetween

همینطور میانگین تغییرات درون گروهی یا MSwithin‌ نیز مطابق با دستور زیر در پایتون بدست می‌آید.

1MSwithin = SSwithin/DFwithin

با محاسبه نسبت این دو مقدار F ratio یا نسبت F حاصل می‌شود. توزیع این آماره مطابق با «توزیع فیشر» (F Distribution) با درجه‌های آزادی به ترتیب صورت و مخرج کسر است.

1F = MSbetween/MSwithin

اگر مقدار F‌ بزرگتر از مقدار متناظر آن در توزیع F باشد، فرض صفر که بیانگر یکسان بودن گروه‌ها است را رد می‌کنیم . به کمک دستور زیر می‌توانیم مقدار احتمال (p-Value) برای آماره F در چنین آزمونی را محاسبه کنیم. البته توجه داشته باشید که در اینجا، به کارگیری تابع stats.f.sf نیازمند کتابخانه SciPy است.

1p = stats.f.sf(F, DFbetween, DFwithin)

برای محاسبه اندازه اثر (Effect Size) یا $$\eta$$‌ کافی است که محاسبه زیر را انجام دهیم تا مقدار مربع اندازه اثر $$\eta^2$$‌ حاصل شود.

1eta_sqrd = SSbetween/SStotal

از طرفی به علت گرایش یا اریبی این شاخص بهتر است برای اندازه اثر، از شاخص دیگری به نام امگا ($$omega$$) استفاده کنیم. شیوه محاسبه مربع این شاخص در زیر دیده می‌شود.

1om_sqrd = (SSbetween - (DFbetween * MSwithin))/(SStotal + MSwithin)

مقدار این شاخص‌ها براساس داده‌های مربوط به مجموعه رشد گیاهان به صورت زیر است.

$$\large F(2,27)=4.846,\;\rho =0.016,\;\eta^2=0.264,\; \omega^2=0.204$$

۳. استفاده از کتابخانه Statsmodels در پایتون

سومین روشی که با آن تحلیل واریانس را در پایتون اجرا می‌کنیم، استفاده از توابع کتابخانه Statsmodels است که کارهای تجزیه و تحلیل واریانس را بسیار ساده کرده و خروجی‌های مطلوبی ارائه می‌کند. در این شیوه، از روش OLS یا همان «رگرسیون کمترین مربعات عادی» (Ordinary Least Square) استفاده شده، سپس برای ترسیم جدول تحلیل واریانس از anova_lm کمک گرفته می‌شود. برای نمایش مدل و رابطه در این توابع بین متغیرهای مستقل و وابسته از نماد ~‌ استفاده می‌شود که دقیقا مشابه با زبان‌برنامه‌نویسی R است. به این ترتیب weight~group نشانگر وجود یا جستجوی مدل بوسیله متغیر مستقل group با متغیر وابسته weight است. کد و دستورات زیر به منظور اجرای این شیوه محاسباتی در پایتون با استاندارد api به کار رفته است.

1import statsmodels.api as sm
2from statsmodels.formula.api import ols
3 
4mod = ols('weight ~ group',
5                data=data).fit()
6                
7aov_table = sm.stats.anova_lm(mod, typ=2)
8print aov_table

خروجی این کد، جدولی است که مقدارهای مربعات تغییرات (Sum_sq)، درجه‌های آزادی (df) و مقدار F و همچنین مقدار احتمال یا همان (PR(>F است. این مشخصات برای گروه‌ها group‌ و باقی‌مانده‌های مدل رگرسیونی (Residual) محاسبه شده است.

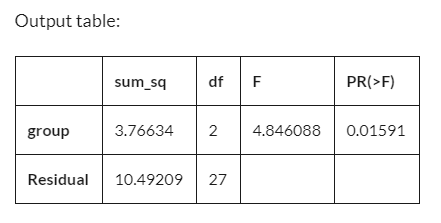
با توجه به مقدار احتمال که برابر با $$0.01591$$ است فرض صفر یعنی برابر بودن میانگین وزن گیاه‌ها در بین تیمارها و گروه کنترل، رد می‌شود.

نکته: توجه داشته باشید که در این حالت شاخص‌های اندازه اثر (Effect Size) محاسبه نخواهد شد. برای بدست آوردن‌ آن‌‌ها باید کد دستوری زیر را نیز به برنامه خود اضافه کنید.

1esq_sm = aov_table['sum_sq'][0]/(aov_table['sum_sq'][0]+aov_table['sum_sq'][1])

۴. استفاده از کتابخانه pyvttbl در پایتون

روش دیگر در انجام محاسبات تحلیل واریانس استفاده از کتابخانه pyvttbl و تابع anova1way است. از آنجایی که این کتابخانه قدیمی است، لازم است که کتابخانه Numpy با نسخه حداکثر 1.1 را نصب داشته باشید. در غیر اینصورت ممکن است با پیغام خطای unsupported operand type(s) for +: ‘float’ and ‘NoneType’‎ مواجه شوید.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

کد زیر به منظور اجرای تحلیل واریانس به کمک این کتابخانه نوشته شده است. همانطور که می‌بینید تابع anova1way به عنوان ورودی یک چارچوب داده (DataFrame) را قبول می‌کند.

1from pyvttbl import DataFrame
2 
3df=DataFrame()
4df.read_tbl(datafile)
5aov_pyvttbl = df.anova1way('weight', 'group')
6print aov_pyvttbl

خروجی این دستورات در ادامه قابل مشاهده است. این صفحه بسیار به صفحاتی که دیگر نرم‌افزارهای محاسبات آماری مانند SPSS یا SAS تولید می‌کنند، شبیه است.

1Anova: Single Factor on weight
2 
3SUMMARY
4Groups   Count    Sum     Average   Variance 
5============================================
6ctrl        10   50.320     5.032      0.340 
7trt1        10   46.610     4.661      0.630 
8trt2        10   55.260     5.526      0.196 
9 
10O'BRIEN TEST FOR HOMOGENEITY OF VARIANCE
11Source of Variation    SS     df    MS       F     P-value   eta^2   Obs. power 
12===============================================================================
13Treatments            0.977    2   0.489   1.593     0.222   0.106        0.306 
14Error                 8.281   27   0.307                                        
15===============================================================================
16Total                 9.259   29                                                
17 
18ANOVA
19Source of Variation     SS     df    MS       F     P-value   eta^2   Obs. power 
20================================================================================
21Treatments             3.766    2   1.883   4.846     0.016   0.264        0.661 
22Error                 10.492   27   0.389                                        
23================================================================================
24Total                 14.258   29                                                
25 
26POSTHOC MULTIPLE COMPARISONS
27 
28Tukey HSD: Table of q-statistics
29       ctrl     trt1       trt2   
30=================================
31ctrl   0      1.882 ns   2.506 ns 
32trt1          0          4.388 *  
33trt2                     0        
34=================================
35  + p < .10 (q-critical[3, 27] = 3.0301664694)
36  * p < .05 (q-critical[3, 27] = 3.50576984879)
37 ** p < .01 (q-critical[3, 27] = 4.49413305084)

تقریبا در این صفحه، همه اطلاعاتی که توسط تحلیل واریانس احتیاج داریم، ظاهر می‌شود. در این خروجی نیز با توجه به جدول ANOVA و مقدار P-value‌ که برابر با $$0.016$$ نشان داده شده، فرض برابری میانگین‌ها در میان گروه‌های تیمار و کنترل رد می‌شود. در جدول انتهایی نیز حتی پس‌آزمون (Post-Hoc) به شیوه توکی (Tukey) صورت گرفته است. این قسمت را با عنوان مقایسه‌های چندتایی پس-آزمون (POSTHOC MULTIPLE COMPARISONS) می‌توانید مشاهده کنید.

توجه دارید که تحلیل واریانس نشان می‌دهد که بین گروه‌ها اختلاف معنی داری وجود دارد یا خیر. در حالیکه پس‌آزمون‌ها یا مقایسه‌های چندتایی امکان می‌دهد که تشخیص دهیم کدام یک از گروه‌ها باعث ایجاد اختلاف شده است. همانطور که در آخرین بخش می‌بینید، علت اختلاف بین گروه‌ها فاصله بین گروه تیمار اول و تیمار دوم است. مشخص است که سطح آزمون در این قسمت کمتر از 0.05 است. بنابراین بین گروه‌های کنترل و گروه تیمار اول و دوم اختلاف معنی‌داری وجود ندارد و یکسان نبودن همه گروه‌ها به علت فاصله و عدم تساوی میانگین بین گروه تیمار اول (trt1) و دوم (trt2) است.

جمع‌بندی و خلاصه

در این نوشتار، ابتدا در مورد مفاهیم اولیه تجزیه واریانس یا مجموع تغییرات در تحلیل واریانس پرداختیم. سپس با استفاده از بعضی توابع و کتابخانه‌های پایتون تحلیل واریانس را برای یک مجموعه داده انجام دادیم. البته در این بین بدون استفاده از کتابخانه‌ها و فقط با استفاده از محاسبات درون پایتون نیز تحلیل واریانس را انجام دادیم. به نظر می‌رسد که نتایج حاصل (بخصوص وجود فاصله بین دو تیمار) توسط نمودار جعبه‌ای ترسیم شده در شکل ۱ نیز تایید می‌شود.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• مجموعه آموزش‌های داده کاوی یا Data Mining در متلب
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش همبستگی و رگرسیون خطی در SPSS
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• تحلیل واریانس (Anova) — مفاهیم و کاربردها
• رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده

^^