جدول توافقی و کاربردهای آن در SPSS — از صفر تا صد
در تحلیلهای آماری، جدول توافقی (Contingency Table) ابزاری برای نمایش اطلاعات ماتریسی است که برطبق فراوانی دو طرفه یا برحسب دو یا چند متغیر کیفی، تنظیم شده است. به همین علت گاهی جدول توافقی را جدول متقاطع (Cross Tabulation) نیز مینامند. در این گونه تحلیلها، محاسبات زیادی براساس جدول توافقی بخصوص روی دادههای کیفی و طبقهای صورت میگیرد. برای مثال برای نشان دادن وجود رابطه یا استقلال بین دو متغیر تصادفی گسسته از نوع کیفی یا شمارشی (Counting Variable) از جدول توافقی و آزمون کای ۲ استفاده میشود. در این نوشتار به بررسی و نحوه ایجاد جدول توافقی (Contingency Table) خواهیم پرداخت. همچنین ضریبهای وابستگی که براساس جدول توافقی محاسبه میشوند، نیز از موضوعاتی است که در این مطلب به آنها اشاره میکنیم.
برای آشنایی اولیه با نحوه محاسبه جدول توافقی بهتر است با جدول فراوانی (Frequency Table) بیشتر آشنا شوید. به این منظور مطالعه جدول فراوانی برای دادههای کیفی و کمی — مثالهای کاربردی توصیه میشود. همچنین برای اطلاع از کاربرد جدول فراوانی دو طرفه و محاسبات مربوط به استقلال متغیرهای کیفی، خواندن نوشتار آزمون نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای۲ نیز خالی از لطف نیست.
از آنجایی که جدول توافقی برای مقادیر طبقهای (اسمی یا ترتیبی) ایجاد میشوند، پس بهتر است با این گونه متغیرها در مطلب جامعه آماری — انواع داده و مقیاسهای آنها بیشتر آشنا شوید. همینطور فراگیری و درک نحوه طبقهبندی کردن متغیرها با خواندن دسته بندی تصویری (Visual Binning) در SPSS — راهنمای کاربردی برایتان سادهتر خواهد بود.
جدول توافقی
زمانی که بخواهیم یک جدول فراوانی دو یا چند متغیره تشکیل دهیم، از جدول توافقی استفاده میکنیم. همانطور که به یاد دارید در جدول فراوانی از رده یا دسته استفاده میشود. اگر مقادیر مشاهدات به صورت گسسته و به صورت طبقهای باشند، برای تشکیل جدول فراوانی مشکلی نداریم ولی زمانی که متغیر دارای مقادیری به صورت پیوسته باشد، برای تشکیل جدول فراوانی باید آن را به صورت دستهای از طبقات درآوریم.
از طرفی کار با چند متغیر به طور همزمان نیز یکی از مسائلی است که در تحلیل چند متغیره مورد بررسی قرار گرفته و شیوههای مبتنی بر جدول فراوانی یا جدول توافقی در آن به وفور به چشم میخورد.
برای مثال یکی از مباحث اصلی در تحلیل چند متغیره، اندازهگیری همبستگی بین متغیرها است تا براساس آن بتوانیم ساختارهای وابستگی (Dependence Structures) را شناسایی و به کار بگیریم. این موضوع در نظریه اطلاع (Information Theory) به کاهش حجم دادهها، بدون کاهش محسوس در اطلاعات ثبت شده منجر خواهد شد.
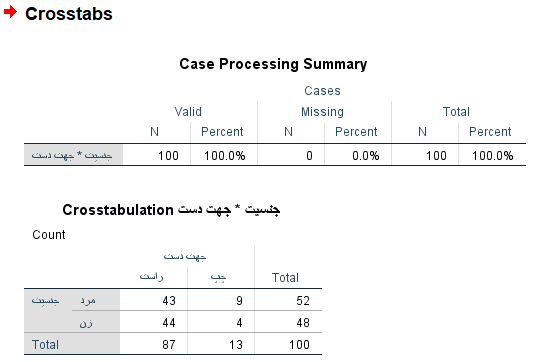
یکی از روشهای ایجاد جدول توافقی، جدول محوری (Pivotal Table) است. به جدول زیر توجه کنید. در این جدول براساس یک نمونه ۱۰۰ تایی از جامعه آماری که شامل افراد جامعه انسانی هستند، چپ یا راست دست بودن آنها را مورد بررسی قرار دادهایم.
جدول ۱: جدول توافقی برای سنجش رابطه جهت دست (دست غالب) و جنسیت
|
جنسیت | راست دست | چپ دست | تعداد کل |
| مرد | 43 | 9 | 52 |
| زن | 44 | 4 | 48 |
| جمع کل | 87 | 13 | 100 |
همانطور که گفته شد، به کمک این جدول میتوان تشخیص داد که آیا بین جنسیت (زن و مرد) و چپ دست بودن رابطهای وجود دارد یا خیر؟ به بیان دیگر میخواهیم بدانیم آیا در بین زنان، چپ دست بودن بیشتر رایج است یا در مردان؟
برای نمایش و همچنین محاسبات مربوط به شاخصهای وابستگی بین متغیرهای کیفی در اینجا از نرمافزار SPSS استفاده میکنیم. ابتدا شیوه ورود و تعریف متغیرها را متذکر میشویم. نحوه پیادهسازی این جدول در SPSS در تصویرهای زیر نشان داده شده است. در ابتدا پنجره Data Editor و برگه Variable View دیده میشود که متغیرها در آن تعریف و مشخص شدهاند. توجه داشته باشید که هر دو متغیر Handedness و Gender کیفی بوده و براساس مقیاس اسمی (Nominal) ایجاد شدهاند.

در تصویر زیر نیز در برگه Value View مقادیر مربوط به متغیرها قرار گرفته است.
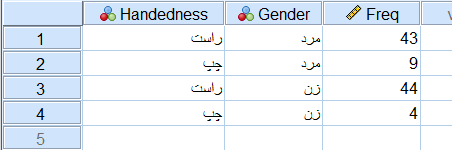
باید توجه داشته باشیم که برای تشکیل جدول توافقی براساس این نوع قرارگیری دادهها، باید سطرهای اطلاعاتی در کاربرگ را با استفاده از متغیر Freq وزندهی کنیم. انجام این کار بوسیله اجرای دستور Weight Cases از فهرست Data صورت میپذیرد. تنظیمات مربوط به پنجره این دستور در تصویر زیر دیده میشود.
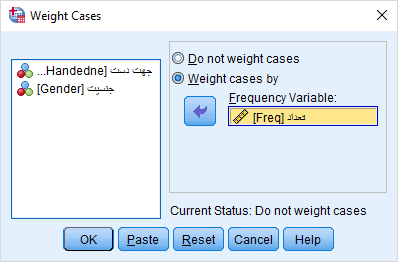
حال جدول توافقی را با استفاده از دستور CrossTabs از فهرست Analysis و زیرگروه Descriptive Statistics اجرا میکنیم. کافی است تنظیمات را مطابق با تصویر زیر انجام دهیم. تا خروجی مناسب حاصل شود.
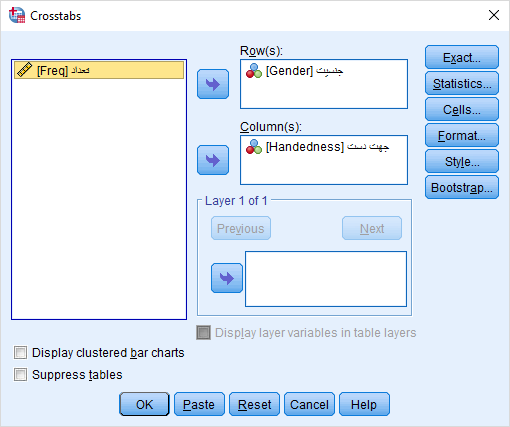
نکته: توجه داشته باشید که از متغیری که برای وزندهی استفاده شده، نباید در تحلیلها استفاده کرد. در اینجا هم با توجه به نقشی که متغیر Freq داشته، در جدول توافقی از آن استفاده نخواهیم کرد بلکه وزندهی مشاهدات براساس این متغیر، اثرش را روی جدول توافقی خواهد گذاشت.
نتیجه اجرای دستورات گفته شده، به صورت یک خروجی در پنجره Output مطابق با تصویر زیر، ظاهر خواهد شد.
نکته: شکل دستوری برای ایجاد این خروجی به قالب Syntax در SPSS به صورت زیر است.
1CROSSTABS
2 /TABLES=Gender BY Handedness
3 /FORMAT=AVALUE TABLES
4 /CELLS=COUNT
5 /COUNT ROUND CELL.ساختار و ویژگیهای جدول توافقی
جدول ۱ و همینطور تصویر بالا را به عنوان مثالی از ساختار یک جدول توافقی در نظر بگیرید. همانطور که مشخص است، جمع سطرها و ستونها و همچنین جمع کل محاسبه شده و در محل مناسب قرار گرفته است. به جمعهای سطر یا ستونها، «مجموع حاشیهای» (Marginal Totals) گفته میشود. جمع کل (جمع سطرهای حاشیهای یا ستونهای حاشیهای) نیز در انتهای جدول قرار گرفته است.
به کمک این جدول میتوان به سرعت سهم یا درصد مردان و زنان را در این نمونه مشخص کرد. همچنین نسبت راستدستها یا چپدستها به راحتی قابل تشخیص است. همانطور که میبینید تقریبا راستدستها 87 درصد مردم را تشکیل میدهند در حالیکه فقط ۱۳ درصد مردم چپدست هستند.
از طرف دیگر با توجه به جمعهای حاشیهای مربوط به سطرها (جمع سطر اول و جمع سطر دوم)، نسبت زنان به مردان تقریبا ۵۰-۵۰ (یا بطور دقیق، 52٪ و 48٪) است. در نتیجه به نظر میرسد نمونهای که تهیه کردیم، نسبت به جنسیت (Gender)، اریبی (Biased) زیادی ندارد.
نکته: حتی اگر جدول توافقی دارای اریبی نسبت به سطر یا ستونها باشد، باز هم نتایج حاصل از جدول توافقی قابل اعتماد بوده و مشکلی بوجود نمیآورد. این امر فقط باعث میشود که توازن در جدول فراوانی وجود نداشته باشد.
به منظور نمایش و محاسبه درصدها برحسب جمع سطر یا ستونها یا حتی جمع کل در پنجره Crosstabs دکمه Cells را انتخاب کنید و گزینههای آن را مانند شکل زیر فعال کنید.
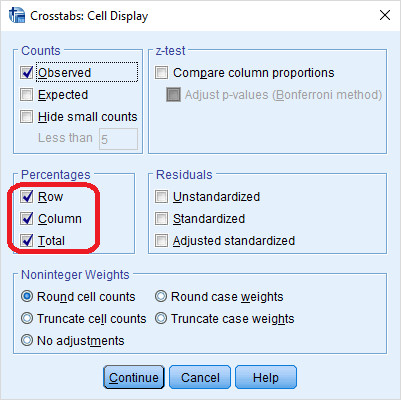
به این ترتیب خروجی جدول فراوانی به صورت زیر در خواهد آمد.
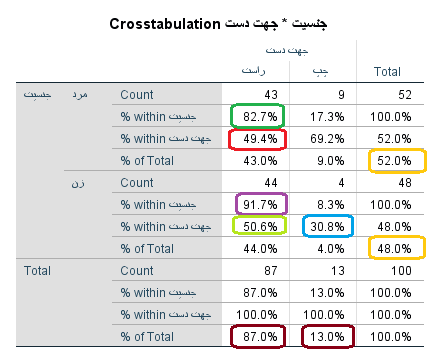
همانطور که دیده میشود، ۸۲٫۷ درصد از مردان، راست دست هستند. این نسبت در زنان 91٫7 درصد است. از طرفی ۱۷٫۳ درصد مردان چپ دست بوده ولی این درصد در نزد زنان فقط ۸٫۳ است. از طرفی ۴۹٫۴ درصد راست دستها از مردان تشکیل شده و ۵۰٫۶ درصد این گروه نیز زنان هستند. همچنین ۳۰٫۸ درصد چپدستها زن و ۶۹٫۲ درصد مرد هستند. درکل ۱۳ درصد از افراد چپ دست و ۸۷ درصد نیز راست دست هستند.
اگر دو متغیر در جدول توافقی به کار رفته باشد، بطوری که سطوح هر یک از آنها در سطر یا ستون قرار گرفته باشند، یک جدول توافقی ساده تشکیل شده است. اگر متغیرهای طبقهای به کار رفته در جدول فراوانی، دو دویی یا «دو وضعیتی» (Dichotomous) باشند، سادهترین جدول توافقی تشکیل خواهد شد. به این ترتیب مشخص است که مقدارهای هر متغیر در این جدول دارای دو سطح خواهند بود. تحلیل وابستگی یا استقلال در چنین جدولهایی توسط آماره و «آزمون مکنمار» (Mac Nemar's test) انجام میشود. هر چه تعداد متغیرها یا تعداد سطوح مقادیر آنها بیشتر باشد، پیچیدگی جدول توافقی بیشتر شده و ممکن است مدلهای بسیار پیچیدهای برای سنجش رابطه بین متغیرها ایجاد شود.
کاربردهای جدول توافقی
جدول توافقی ساختاری است که به علت ارتباطی که بین سطرها و ستونهای آن وجود دارد، کاربردهای متعدد و زیادی دارد. در ادامه به بعضی از این کاربردها، به صورت فهرستوار اشاره میکنیم. همچنین در ادامه شاخصهای وابستگی که توسط جدول توافقی قابل محاسبه هستند، معرفی و مورد بررسی قرار میگیرند.
- ماتریس درهمریختگی (Confusion Matrix).
- جدول محوری (Pivot Table) در کاربرگها و صفحه گستردهها و ایجاد جدولهای توافقی.
- جدولها یا مکعبهای پردازش برخط (OLAP Cube) در علم داده (Data Science).
- دادههای پانلی (Panel Data) در تحلیلهای چند متغیره وابسته به زمان.
- برای متغیرهای گسسته، محاسبه شاخصهای وابستگیهای غیرخطی در تحلیلهای چند متغیره آماری، توسط جدول توافقی صورت میگیرد. این شاخصها اغلب برحسب آمارهای که دارای توزیع کای ۲ است بدست میآیند. مانند آزمون کای ۲ برای استقلال بین دو متغیر تصادفی طبقهای.
آمارههای وابسته به جدول توافقی
در ادامه به بعضی از ضرایب آمارههای وابستگی که برحسب جدول توافقی محاسبه میشوند خواهیم پرداخت. این ضرایب معمولا برای سنجش همبستگی بین متغیرهای طبقهای به کار میروند.
نسبت بختها (Odds Ratio)
سادهترین «اندازه وابستگی» (Dependency Measure) برای جدول توافقی $$2 \times 2$$ نسبت بخت (Odd Ratio) است. فرض کنید دو پیشامد A و B مورد بررسی قرار گرفتهاند. نسبت بختها، همان نسبت احتمال رخداد هر یک از این پیشامدها است. به این ترتیب میتوان نسبت بخت را براساس تقسیم بخت یا شانس رخداد پیشامد A در حضور پیشامد B بر شانس رخداد پیشامد A در عدم رخداد پیشامد B در نظر گرفت. البته در صورت وجود تقارن میتوان این نسبت را برحسب پیشامد B نیز به صورت نسبت شانس رخداد B در حضور و عدم حضور A تنظیم کرد.
برای مثال فرض کنید که جدول زیر مربوط به احتمال رخداد هر یک از پیشامدهای توام A و B باشد. به این ترتیب $$p_{ij}$$ برابر است با احتمال توام پیشامد A و پیشامد B. واضح است که مقدار $$i$$ و $$j$$ دو مقدار صفر و یک را میپذیرند زیرا هر پیشامد یا دارای وضعیت رخداد ($$1$$) یا عدم رخداد ($$0$$) است.
$$\large {\displaystyle {\begin{array}{c|cc}&B=1&B=0\\\hline A=1&p_{11}&p_{10}\\ A=0&p_{01}&p_{00}\end{array}}}$$
به این ترتیب نسبت بخت به صورت زیر محاسبه خواهد شد.
$$\large OR=\dfrac{\dfrac{p_{11}}{p_{10}}}{\dfrac{p_{01}}{p_{00}}}=\dfrac{p_{11}p_{00}}{p_{10}p_{01}}$$
مطابق با جدول 2 نسبت بخت دست غالب راست به چپ برابر است با:
$$\large OR = \dfrac{0.87}{0.13}= 6.69$$
همچنین نسبت بخت برای زنان و مردان نیز برابر است با:
$$\large OR = \dfrac{0.52}{0.48}= 1.083$$
ولی نسبتبخت راست دست به چپ دست بودن بین مردان برابر است با:
$$\large OR= \dfrac{0.49}{0.69} = 0.714$$
از طرفی نسبتبخت راستدست بودن به چپ دست بودن در بین زنان نیز به صورت زیر خواهد بود:
$$\large {\displaystyle OR={\dfrac {0.44}{0.04}}=11}$$
همانطور که مشاهده میکنید، ممکن است نسبتبختها، بزرگتر از یک باشد.
اگر دو پیشامد A و B مستقل از یکدیگر باشند، نسبتبخت به ۱ نزدیک خواهد شد و برعکس. به این معنی که اگر نسبتبخت، برابر با ۱ باشد، میتوان نتیجه گرفت که دو پیشامد مستقل هستند. اگر مقدار نسبتبخت، بزرگتر از یک باشد، بیانگر آن است که دو پیشامد به صورت مستقیم و مثبت با یکدیگر ارتباط دارند. همچنین مقدار کمتر از ۱ بیانگر ارتباط منفی بین دو پیشامد است.
با توجه به این مثال به نظر میرسد که پدیده راست دستی در مردان نسبت به زنان کمتر است و در نتیجه بخت چپدست بودن در مردان بیشتر از زنان است.
محاسبه نسبت بخت در نرمافزار SPSS توسط دستور Crosstabs به شکل زیر صورت میگیرد.
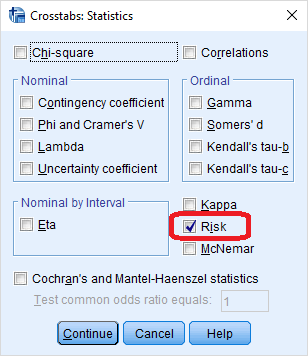
به این ترتیب خروجی مطابق با تصویر زیر حاصل میشود. البته دقت کنید که در این جا نسبت بخت براساس سطرها محاسبه میشود.
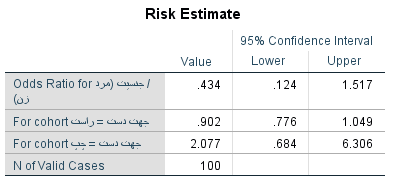
در صورتی که جای متغیرهای سطر و ستون را در جدول توافقی عوض کنیم، خروجی به شکل زیر ظاهر خواهد شد.
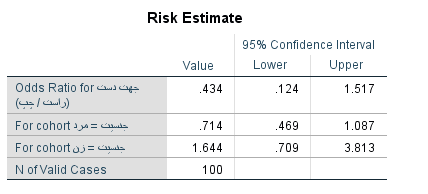
ضریب فی (Phi Coefficient)
یکی دیگر از شاخصهای مربوط به اندازهگیری وابستگی در جدول توافقی $$2 \times 2$$، ضریب فی (Phi Coefficient) است که با نماد $$\phi$$ نشان داده میشود. همانطور که مشخص است این ضریب برای اندازهگیری وابستگی بین دو متغیر با مقادیر دو وضعیتی (Dichotomous) به کار میرود.
نحوه محاسبه این شاخص برحسب مقدار آماره کای ۲ (Chi Squared) بوده و به شکل زیر است.
$$\large {\displaystyle \phi =\pm {\sqrt {\frac {\chi ^{2}}{n}}}}$$
مشخص است که در این رابطه، مقدار $$n$$ همان مجموع کل در جدول توافقی است. این شاخص در بازه $$[-1,1]$$ تغییر کرده و زمانی که با ۱ برابر باشد، نشان از همبستگی مثبت و مستقیم بین دو متغیر است و در صورتی که برابر با ۱- باشد، همبستگی منفی و معکوس را نشان میدهد. همچنین در صورتی که ضریب فی، برابر با صفر یا نزدیک به آن باشد، میتوان عدم وابستگی بین دو متغیر را نتیجه گرفت.
مقدار ضریب فی را برای یک جدول ۲ × ۲ با توجه به فراوانیها میتوان به صورت زیر در نظر گرفت.
| total | y=0 | y=1 | |
| $$n_{1 \bullet}$$ | $$n_{10}$$ | $$n_{11}$$ | x=1 |
| $$n_{\bullet 1}$$ | $$n_{00}$$ | $$n_{01}$$ | x=0 |
| $$n_{\bullet \bullet}=n$$ | $$n_{\bullet 0}$$ | $$n_{\bullet 1}$$ | Total |
در این صورت مقدار ضریب فی به صورت زیر محاسبه خواهد شد. توجه داشته باشید که منظور از $$n_{\bullet 0}$$ جمع روی ستون $$y=0$$ و همچنین $$n_{\bullet 1}$$ جمع روی ستون $$y=1$$ است. همینطور $$n_{1 \bullet}$$ جمع روی سطر $$x=1$$ و $$n_{۰ \bullet}$$ جمع روی سطر $$x=۰$$ است. جمع کل نیز به شکل $$n_{\bullet \bullet}=n$$ نشان داده شده است که بیانگر جمع روی همه سطرها و ستونها است.
$$\large{\displaystyle \phi ={\frac {n_{11}n_{00}-n_{10}n_{01}}{\sqrt {n_{1\bullet }n_{0\bullet }n_{\bullet 0}n_{\bullet 1}}}}}$$
اگر مقدار احتمالهای حاشیهای جدول توافقی برابر با 0٫5 باشد، یا عناصر روی قطر اصلی، صفر باشند، ضریب فی، برابر با ۱ یا ۱- خواهد شد.
نکته: علامت ضریب فی بسته به تقاضل حاصلضرب عناصر قطر اصلی و فرعی است. به این معنی که اگر حاصل ضرب قطر فرعی را از حاصل ضرب قطر اصلی کم کنیم، نتیجه حاصل هر علامتی داشته باشد، ضریب فی نیز همان علامت را خواهد داشت.
به این ترتیب براساس جدول ۱، مقدار ضریب فی برای سنجش ارتباط بین جهت دست (دست غالب) و جنسیت به صورت زیر بدست خواهد آمد.
$$\large{\displaystyle \phi ={\frac {(43\times 4)-(9 \times 44)}{\sqrt {52 \times 48 \times 87 \times 4}}}= -0.133}$$
نکته: برای محاسبه ضریب فی میتوانید از رابطه زیر نیز استفاده کنید که البته فقط احتیاج به مجموع سطر و ستونها و البته فراوانی گروه هدف دارد.
$$\large{\displaystyle \phi ={\frac {nn_{11}-n_{1\bullet }n_{\bullet 1}}{\sqrt {n_{1\bullet }n_{\bullet 1}(n-n_{1\bullet })(n-n_{\bullet 1})}}}}$$
ضریب کرامر (Cramer's V) و ضریب توافق C
ضرایب معروف دیگری نیز برای سنجش وابستگی بین دو متغیر در جدول توافقی وجود دارد که در این میان میتوان به ضریب کرامر و ضریب توافق C اشاره کرد.
ضریب کرامر را با $$V$$ و ضریب توافق را با حرف $$C$$ نشان میدهند. در ادامه نحوه محاسبه هر یک از آنها را برحسب آماره کای ۲ (کای ۲ پیرسون) مشاهده میکنید.
$$\large C=\sqrt{\frac{\chi^2}{n+\chi^2}} $$
$$\large V={\sqrt {{\frac {\chi ^{2}}{n(k-1)}}}} $$
نکته: منظور از $$k$$ در محاسبه ضریب کرامر، تعداد سطرها یا ستونهای جدول توافقی است. واضح است که در صورت مربعی بودن جدول توافقی این تعداد سطرها و ستونها یکسان است. ولی اگر جدول توافقی مربعی نباشد، $$k$$ کوچکترین مقدار از تعداد سطرها یا ستونها خواهد بود.
هر دو شاخص کرامر و ضریب توافق، مقدارهایی مثبت هستند و جهت وابستگی را مشخص نمیکنند. متاسفانه ضریب C همیشه دارای کران مشخص و ثابتی نیست. برای جدولهای ۲×۲، بیشترین مقدار آن 0٫707 خواهد بود در حالیکه برای جدولهای ۴×4، بیشترین مقدار 0٫870 است. در نتیجه گاهی برای آن یک ضریب تصحیح نیز به کار میبرند که در این صورت میتوان رابطه زیر را برای C اصلاح شده در نظر گرفت. البته توجه داشته باشید که در اینجا جدول توافقی باید مربعی بوده و $$k$$ سطر یا ستون داشته باشد.
$$\large C= {\displaystyle {\sqrt {\frac {k-1}{k}}}}\sqrt{\frac{\chi^2}{N+\chi^2}}$$
در صورتی که تعداد سطرها با ستونهای جدول توافقی یکسان نباشد، ضریب اصلاح به صورت زیر خواهد بود. توجه دارید که $$r$$ بیانگر تعداد سطرها است و $$c$$ نیز تعداد ستون را در جدول توافقی مشخص کرده است.
$$\large C= {\displaystyle {\sqrt[{\scriptstyle ^4\;\;\;}]{{r-1 \over r}\times {c-1 \over c}}}}\sqrt{\frac{\chi^2}{N+\chi^2}}$$
فرض کنید یک نمونه تصادفی با حجم $$n$$ داریم و $$n_{ij}$$ نیز تعداد فراوانی (توزیع توام) در سطح $$i$$ام از متغیر A و سطح $$j$$ام از متغیر B است. اگر تعداد سطرها $$r$$ و تعداد ستونها نیز $$c$$ باشد، واضح است که $$i=1,\ldots ,r;j=1,\ldots ,c$$
$$\large n_{{ij}}= \text{number of times the values} {\displaystyle (A_{i},B_{j})}$$
ضریب کای ۲ برای چنین جدولی به صورت زیر محاسبه خواهد شد:
$$\large \chi ^{2}=\sum _{{i,j}}{\frac {(n_{{ij}}-{\frac {n_{{i.}}n_{{.j}}}{n}})^{2}}{{\frac {n_{{i.}}n_{{.j}}}{n}}}}$$
به این ترتیب ضریب کرامر V را بوسیله رابطه زیر محاسبه خواهیم کرد:
$$\large V={\sqrt {{\frac {\chi ^{2}/n}{\min(k-1,r-1)}}}={\sqrt {\frac {\phi ^{2}}{\min(k-1,r-1)}}}}$$
پس میتوانیم ضریب کرامر را از روی ضریب فی بدست آوریم و برعکس، ضریب فی را از روی ضریب کرامر محاسبه کنیم. به کمک نرمافزار محاسبات آماری SPSS و براساس جدول 1، ضریب کرامر V و ضریب توافق C قابل محاسبه است. فقط کافی است که پس از اجرای دستور Crosstabs، در داخل پنجره Statistics تنظیمات زیر را درخواست کنید.
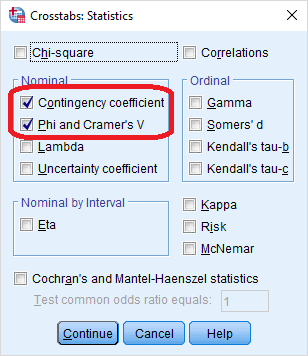
خروجی به این ترتیب به صورت زیر خواهد بود.

همانطور که مشاهده میکنید، ضریب فی و ضریب کرامر با توجه به اطلاعات جدول 1 و مربعی و $$2 \times 2$$ بودن آن و بدون در نظر گرفتن علامت این ضرایب، به یکدیگر بسیار نزدیک هستند. همچنین مقدار ضریب توافق نیز به ضریب کرامر شبیه است.
اگر بخواهید این دستورات را در محیط Syntax در نرمافزار SPSS اجرا کنید، باید کدهای زیر را وارد و اجرا کنید.
1CROSSTABS
2 /TABLES=Gender BY Handedness
3 /FORMAT=AVALUE TABLES
4 /STATISTICS=CC PHI
5 /CELLS=COUNT
6 /COUNT ROUND CELL.خلاصه و جمعبندی
در این نوشتار به بررسی جدول توافقی و ساختار آن بخصوص در حالتی که جدول توافقی به صورت مربعی و ۲×۲ بود، پرداختیم. همچنین شاخصهای وابستگی که از طریق جدول توافقی قابل اندازهگیری هستند نیز مورد بررسی قرار گرفت. بوسیله مثالهایی، شیوه محاسبه هر یک از این شاخصها در محیط SPSS نیز معرفی شد. در نوشتارهای بعدی نحوه محاسبه این شاخصها را در نرمافزارهای آماری بخصوص SPSS فرا میگیریم.
اگر به یادگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:










