روش پس انتشار — از صفر تا صد

انتشار رو به عقب خطاها که به اختصار «پس انتشار» (Backpropagation) نامیده می‌شود، الگوریتمی برای یادگیری نظارتی شبکه عصبی با استفاده از گرادیان کاهشی است. در این روش، برای یک شبکه عصبی مصنوعی و تابع خطای مشخص، گرادیان تابع خطا نسبت به وزن‌های شبکه عصبی محاسبه می‌شود. الگوریتم پس انتشار تعمیمی از قانون دلتا برای پرسپترون‌ها به شبکه‌های عصبی پیشخور چندلایه است.

واژه «پس‌رو» یا «رو به عقب» (Backward) که بخشی از اصطلاح پس انتشار است، در واقع از این موضوع می‌آید که محاسبه گرادیان به صورت رو به عقب در شبکه انجام می‌شود و گرادیان لایه خروجی وزن‌ها در ابتدا و گرادیان لایه ورودی در آخر انجام می‌شود؛ بدین صورت که از محاسبات مشتق جزئی گرادیان یک لایه برای گرادیان لایه قبلی استفاده می‌شود. این حرکت رو به عقب اطلاعات خطا، منجر به محاسبه کارآمد گرادیان در هر لایه نسبت به حالتی می‌شود که در آن گرادیان لایه‌ها به صورت جداگانه به دست می‌آید.

با توجه به استقبال گسترده از شبکه‌های عصبی عمیق برای بازشناسی تصویر و  گفتار، محبوبیت روش پس انتشار اخیراً افزایش یافته است. پس انتشار یک الگوریتم کارآمد محسوب می‌شود و پیاده‌سازی‌های مدرن از GPUهای تخصصی، برای بهبود بیشتر عملکرد از آن بهره می‌گیرند.

تاریخچه روش پس انتشار

پس انتشار در دهه ۱۹۷۰ به عنوان یک روش بهینه‌سازی عمومی برای انجام مشتق‌گیری خودکارِ توابعِ تو در توی مختلط معرفی شد. با این حال، در سال ۱۹۸۶ با انتشار مقاله‌ای از «روملهارت» (Rumelhart)، «هینتون» (Hinton) و «ویلیامز» (Williams)‌ با عنوان «نمایش‌های یادگیری با خطاهای پس انتشار» اهمیت این الگوریتم توسط جامعه یادگیری ماشین مورد توجه قرار گرفت.

فیلم آموزش شبکه های عصبی مصنوعی در متلب در فرادرس

کلیک کنید

پژوهشگران از مدت‌ها قبل علاقه‌مند بودند راهی برای آموزش شبکه‌های عصبی چندلایه پیدا کنند تا بتواند به طور خودکار «نمایش‌های داخلی» مناسب را به دست آورند (یعنی ویژگی‌هایی که یادگیری را آسان‌تر و دقیق‌تر می‌کنند). این ویژگی‌ها را می‌توان به عنوان ورودی یک گره خاص در نظر گرفت که آن گره را فعال می‌کند (یعنی باعث می‌شود که مقدار مثبت آن نزدیک به ۱ باشد). از آنجا که فعال شدن یک گره به وزن‌ها و بایاس‌های وارد شونده آن بستگی دارد، پژوهشگران می‌گویند اگر وزن‌ها و بایاس سبب شوند این گره هنگام حضور این ویژگی در ورودی خود فعال شود، گره ویژگی را آموخته است.

تا دهه ۱۹۸۰، ویژگی‌ها به صورت دستی در بسیاری از زمینه‌ها، به ویژه در بینایی کامپیوتر، تبدیل به استاندارد عملی شده بود، زیرا متخصصان از آزمایش‌ها دریافته‌ بودند که ویژگی‌ها (به عنوان مثال خطوط، حلقه‌ها، لبه‌ها و حباب در بینایی کامپیوتر) یادگیری را ساده‌تر می‌کنند. با وجود این، ویژگی‌های موفق دستی به دانش و تمرین زیادی نیاز داشت و مهم‌تر از آن، از آنجا که خودکار نبود، معمولاً بسیار کند عمل می‌کرد.

پس انتشار یکی از نخستین روش‌هایی بود که نشان داد شبکه‌های عصبی مصنوعی می‌توانند نمایش داخلی مناسب را یاد بگیرند (یعنی لایه‌های پنهان آن‌ها، ویژگی‌های نابدیهی و مبهم را یاد بگیرند). متخصصانی که شبکه‌های پیشخور چندلایه را با استفاده از پس انتشار آموزش دادند، دریافتند که بسیاری از گره‌ها ویژگی‌ها را شبیه به آنچه توسط متخصصان انسانی طراحی شده است، یاد گرفته‌اند. حتی مهم‌تر از آن، به دلیل کارایی الگوریتم و این واقعیت که متخصصان دیگر نیازی به یافتن ویژگی‌های مناسب نداشتند، پس انتشار این امکان را داد که شبکه‌های عصبی مصنوعی در زمینه‌های بسیار وسیع‌تری که قبل‌تر گرفتار محدودیت‌های زمانی و هزینه‌ای بودند، به کار گرفته شوند.

تعریف پس انتشار

پس انتشار شبیه به محاسبه قانون دلتا برای یک شبکه پیشخور چندلایه است. بنابراین، مانند قاعده دلتا، پس انتشار به سه چیز نیاز دارد:

• (۱)‌ مجموعه داده شامل زوج‌ مرتب‌های $$\big ( \overrightarrow { x _ i } , \overrightarrow { y _ i } \big )$$ است، که در آن، $$\overrightarrow { x _ i }$$ ورودی و $$\overrightarrow { y _ i }$$ خروجی مطلوب شبکه به ازای ورودی $$\overrightarrow { x _ i }$$ است. مجموعه زوج‌های ورودی-خروجی با اندازه $$N$$ را با $$X = \Big \{ \big ( \overrightarrow { x _ 1 } , \overrightarrow { y _ 1 } \big ) , \dots , \big ( \overrightarrow { x _ N } , \overrightarrow { y _ N } \big ) \Big \}$$  مشخص می‌کنیم.
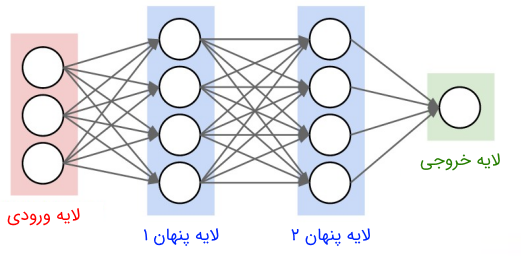
• (۲) پارامترهای یک شبکه عصبی پیشخور را به صورت تجمعی با $$\theta$$ نشان می‌دهیم. در پس انتشار، پارامترهای اصلی $$w _ { i j } ^ k$$ (وزن‌های بین گره $$j$$ در لایه $$l _ k$$ و گره $$i$$ در لایه $$l _ { k- 1 }$$ و $$b _ i ^ k$$ بایاس گره $$i$$ در لایه $$l _ k$$ هستند. اتصالی بین گره‌های یک لایه وجود ندارد و لایه‌های متفاوت به طول کامل به هم اتصال دارند.
• (۳) تابع خطای $$E ( X, \theta )$$ خطای بین خروجی مطلوب $$\overrightarrow { y _ i }$$ و خروجی محاسبه شده $$\hat { \overrightarrow { y _ i } }$$ شبکه عصبی به ازای ورودی $$\overrightarrow { x _ i }$$ را برای یک مجموعه از زوج‌های ورودی-خروجی $$\big ( \overrightarrow { x _ i }, \overrightarrow { y _ i } \big ) \in X$$ و مقدار خاص پارامتر $$\theta$$ تعریف می‌کند.

آموزش یک شبکه عصبی با گرادیان کاهشی نیازمند محاسبه گرادیان خطای $$E (X, \theta )$$ نسبت به وزن‌های $$w_{ij}^k$$ و بایاس‌های $$b_i^k$$ است. بر اساس نرخ یادگیری $$\alpha$$، هر تکرار گرادیان کاهشی وزن‌ها و بایا‌س‌ها (که به صورت تجمعی با $$\theta$$ مشخص شده‌اند) را بر اساس رابطه زیر به‌روز می‌کند:‌

$$\large \theta ^ { t + 1 } = \theta ^ { t } - \alpha \frac { \partial E ( X , \theta ^ { t } ) } { \partial \theta } ,$$

که در آن، $$\theta ^ t$$ پارامترهای شبکه عصبی را برای تکرار $$t$$ در گرادیان کاهشی مشخص می‌کند.

هدف چیست؟

همان‌طور که در بخش قبلی ذکر شد، یکی از مشکلات اساسی آموزش شبکه‌های عصبی پیشخور چندلایه تصمیم‌گیری در مورد چگونگی یادگیری نمایش داخلی مناسب است (یعنی وزن‌ها و بایاس‌های گره‌های لایه پنهان چه باید باشد). برخلاف پرسپترون که از قانون دلتا برای تقریب یک خروجی هدف تعریف شده است، گره‌های لایه پنهان خروجی هدف ندارند، زیرا از آن‌ها به عنوان گام‌های میانی در محاسبه استفاده می‌شود.

از آنجا که گره‌های لایه پنهان خروجی هدف ندارند، نمی‌توان یک تابع خطا را که مخصوص آن گره باشد، تعریف کرد. در عوض، هر تابع خطایی برای آن گره به مقادیر پارامترهای موجود در لایه‌های قبلی (زیرا لایه‌های قبلی، ورودی آن گره را تعیین می‌کنند) و لایه‌های بعدی (زیرا خروجی آن گره بر محاسبه تابع خطای $$E(X, \theta )$$ تأثیر می‌گذارد) بستگی دارد. این اتصال پارامترها بین لایه‌ها می‌تواند ریاضیات مسئله را بسیار دشوار  کند (در درجه اول در نتیجه استفاده از قانون ضرب که در ادامه مورد بحث قرار می‌گیرد)، و در صورت عدم اجرای هوشمندانه، موجب کندی محاسبات گرادیان نزولی نهایی شود. پس‌انتشار با ساده کردن ریاضیات گرادیان نزولی، هر دو مشکل را برطرف می‌کند، ضمن اینکه محاسبه کارآمد آن را نیز تسهیل می‌کند.

تعریف رسمی 

فرمول‌بندی زیر برای شبکه عصبی با یک خروجی است، اما این الگوریتم با استفاده مداوم از قاعده مشتق زنجیره‌ای و قانون توان قابلیت پیاده‌سازی روی یک شبکه با هر تعداد خروجی را دارد. بنابراین، برای همه مثال‌های زیر، زوج ورودی-خروجی به فرم $$( \overrightarrow { x } , y )$$ است، یعنی مقدار هدف $$y$$ یک بردار نیست.

با یادآوری فرمول کلی برای شبکه عصبی پیشخور،

• $$w _ {ij} ^ k$$: وزن گره $$j$$ در لایه $$l _ k$$ برای گره وارد شونده $$i$$
• $$b _ i ^ k$$: بایاس گره $$i$$ در لایه $$l _ k$$
• $$a _ i ^ k$$: مجموع حاصلضرب به علاوه بایاس (فعال‌سازی) برای گره $$i$$ در لایه $$l _ k$$
• $$o _ i ^ k$$: خروجی گره $$i$$ در لایه $$l _ k$$
• $$r _ k$$: تعداد گره‌های لایه $$l _ k$$
• $$g$$: تابع فعال‌سازی گره‌های لایه پنهان
• $$g_o$$: تابع فعال‌سازی گره‌های لایه خروجی

تابع خطا در پس انتشار کلاسیک، خطای میانگین مربعات است:

$$\large E ( X , \theta ) = \frac { 1 } { 2 N } \sum _ { i = 1 } ^ N \left ( \hat { y _ i } - y _ i \right ) ^ 2 ,$$

که در آن، $$y _ i$$ مقدار هدف زوج ورودی-خروجی $$( \overrightarrow { x _ i } , y _ i )$$ و $$\hat { y _ i }$$ خروجی محاسبه شده شبکه برای ورودی $$\overrightarrow { x _ i }$$ است.

می‌توان از توابع خطای دیگری نیز استفاده کرد، اما ارتباط تاریخی خطای میانگین مربعات با پس انتشار و خصوصیات ریاضی جذابش، آن را یک گزینه مناسب برای یادگیری این روش قرار داده است.

محاسبه گرادیان

استخراج الگوریتم پس انتشار کاملاً ساده است و از کاربرد قاعده زنجیره‌ای و قاعده ضرب در حساب دیفرانسیل نتیجه می‌شود. استفاده از این قوانین به مشتق‌گیری تابع فعال‌سازی بستگی دارد و این یکی از دلایلی است که از تابع پله هویساید استفاده نمی‌شود (ناپیوسته بودن و در نتیجه غیر مشتق‌ناپذیر بودن).

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python در فرادرس

کلیک کنید

مقدمات

در ادامه این بخش، مشتق تابع $$f ( x )$$ را با $$f'(x)$$ نمایش خواهیم داد، بنابراین مشتق تابع سیگموئید $$\sigma^\prime (x)$$ خواهد بود.

برای ساده‌سازی ریاضیاتی بیشتر، بایاس $$b _ i ^ k$$ گره $$i$$ در لایه $$k$$ به صورت $$w _ { 0 i } ^ k$$ با یک خروجی ثابت $$o _ 0 ^ { k-1} = 1$$ برای گره $$0$$ در لایه $$k - 1$$ در وزن‌ها گنجانده شده است. بنابراین، داریم:

$$\large w _ { 0 i } ^ k = b _ i ^ k .$$

برای مشاهده برابر بودن نتیجه ساده‌سازی با فرمول اصلی، توجه داشته باشید:

$$\large a _ i ^ k = b _ i ^ k + \sum _ { j = 1 } ^ { r _ { k - 1 } } w _ { j i } ^ k o _ j ^ { k - 1} = \sum _ { j = 0 } ^ { r _ { k - 1 } } w _ { j i } ^ k o _ j ^ { k - 1 } ,$$

که سمت چپ، فرمول اصلی و سمت راست، فرمول جدید است.

با استفاده از فرمول‌بندی بالا،‌ پس انتشار با محاسبه $$\frac { \partial E } { \partial w _ { i j } ^ k }$$ برای هر وزن $$w _ { i j } ^ k$$، تابع زیر را نسبت به وزن‌های شبکه عصبی کمینه می‌کند:

$$\large E ( X , \theta ) = \frac { 1 } { 2 N } \sum _ { i = 1 } ^ N \left ( \hat { y _ i } - y _ i \right ) ^ { 2 }$$

از آنجا که تابع خطا را می‌توان به مجموع جملات خطای جداگانه برای هر زوج ورودی-خروجی جداگانه تجزیه کرد، مشتق را می‌توان با توجه به هر زوج ورودی-خروجی به صورت جداگانه محاسبه و سپس در انتها ترکیب کرد (با توجه به اینکه مشتق مجموع توابع برابر با مجموع مشتق هر تابع است):

$$\large \frac { \partial E ( X , \theta ) } { \partial w _ { i j } ^ k } = \frac { 1 } { N } \sum _ { d = 1 } ^ N \frac { \partial }{ \partial w _ { i j } ^ k } \left ( \frac { 1 } { 2 } \left ( \hat { y _ d } - y _ d \right ) ^ { 2 } \right ) = \frac { 1 }{ N } \sum _ { d = 1 } ^ N \frac { \partial E _ d } { \partial w _ { i j } ^ k } .$$

بنابراین، برای مشتق‌گیری، الگوریتم پس انتشار تنها با یک زوج ورودی-خروجی سر و کار خواهد داشت. فرم کلی برای همه زوج‌های ورودی-خروجی در $$X$$ با ترکیب گرادیان‌های جداگانه ایجاد می‌شود. بنابراین، تابع خطای مورد نظر برای مشتق‌گیری به صورت زیر است:

$$\large E = \frac { 1 } { 2 } \left ( \hat { y } - y \right ) ^ { 2 } ,$$

که در آن، اندیس $$d$$ در $$E_d$$، $$\hat { y _ d }$$ و $$y _ d$$ برای سادگی حذف شده است.

مشتقات تابع خطا

استخراج الگوریتم پس انتشار با اعمال قاعده زنجیره‌ای به مشتق جزئی تابع خطا آغاز می‌شود:‌

$$\large \frac { \partial E } { \partial w _ { i j } ^ k } = \frac { \partial E } { \partial a _ j ^ k } \frac { \partial a _ j ^ k } { \partial w _ { i j } ^ k } ,$$

که $$a _ j ^ k$$ فعال‌سازی (مجموع حاصل‌ضرب به علاوه بایاس) گره $$j$$ در لایه $$k$$ قبل از عبور از تابع تابع فعال‌سازی غیرخطی (در این حالت، تابع سیگموئید) برای تولید خروجی است. این تجزیه مشتق جزئی اساساً بیان می‌کند که تغییرات تابع خطای ناشی وزن، برابر با حاصل‌ضرب تغییرات تابع خطای $$E$$ ناشی از فعال‌سازی $$a _ j ^ k$$ و تغییرات فعال‌سازی $$a _ j ^ k$$ ناشی از وزن $$w _ { i j } ^ k$$ است.

جمله اول معمولاً خطا نامیده می‌شود و به دلیلی که در ادامه می‌گوییم و آن را به صورت زیر می‌نویسیم:

$$\large \delta _ j ^ k \equiv \frac { \partial E } { \partial a _ j ^ k } .$$

جمله دوم را می‌توان از معادله $$a _ j ^ k$$ بالا محاسبه کرد:

$$\large \frac { \partial a _ j ^ k } { \partial w _ { i j } ^ k } = \frac { \partial } { \partial w _ { i j } ^ k } \left ( \sum _ { l = 0 } ^ { r _ { k - 1 } } w _ { l j } ^ k o _ l ^ { k - 1 } \right ) = o _ i ^ { k - 1 } .$$

بنابراین، مشتق جزئی تابع خطای $$E$$ نسبت به وزن $$w _ { i j } ^ k$$ برابر است با:

$$\large \frac { \partial E } { \partial w _ { i j } ^ k } = \delta _ j ^ k o _ i ^ { k - 1 } .$$

در نتیجه، مشتق جزئی یک وزن یک حاصل‌ضرب از جمله خطای $$\delta _ j ^ k$$ در گره $$j$$ از لایه $$k$$ و خروجی $$o _ i ^ { k - 1 }$$ از گره $$i$$ در لایه $$k - 1$$ است. این موضوع یک درک شهودی ایجاد می‌کند، زیرا وزن $$w _ { i j } ^ k$$ خروجی گره $$i$$ در لایه $$k - 1$$ را به ورودی گره $$j$$ در لایه $$k$$ در محاسبات گراف متصل می‌کند.

توجه به این نکته ضروری است که مشتقات جزئی فوق بدون در نظر گرفتن یک تابع خطا یا تابع فعال‌سازی خاص محاسبه شده است. اما از آنجا که جمله خطای $$\delta _j ^ k$$ هنوز هم باید محاسبه شود و به تابع خطای $$E$$ بستگی دارد، در این مرحله لازم است توابع خاص برای هر دوی این‌ها معرفی شود. همان‌طور که قبلاً ذکر شد، پس انتشار کلاسیک از تابع خطای میانگین مربعات (که این تابع خطای مربعات برای زوج ورودی-خروجی است) و تابع فعال‌سازی سیگموئید استفاده می‌کند.

محاسبه خطای $$\delta _ j ^ k$$ نشان خواهد داد که به مقادیر جملات خطا در لایه بعدی بستگی دارد. بنابراین، محاسبه جملات خطا از لایه خروجی به سمت لایه ورودی به عقب ادامه می‌یابد. اینجاست که پس انتشار یا انتشار خطاها به عقب معنا پیدا می‌کند.

لایه خروجی

پس انتشار با شروع از لایه خروجی، مقدار $$\delta _ 1 ^ m$$ را تعریف می‌کند که $$m$$ لایه آخر است (اندیس $$1$$ است و $$j$$ نیست، زیرا این مشتق با یک شبکه عصبی تک‌خروجی سر و کار دارد، بنابراین، تنها گره تک‌خروجی $$j = 1$$ وجود دارد). برای مثال، یک شبکه عصبی چهار لایه در لایه خروجی دارای $$m=  3$$،‌ در لایه دوم $$m = 2$$ و... خواهد بود). با بیان تابع خطای $$E$$ برحسب مقدار $$a _ 1 ^ m$$ (از آنجا که $$\delta _ 1 ^ m$$ یک مشتق جزئی نسبت به $$a _ 1 ^ m$$ است)، داریم:

$$\large E = \frac { 1 } { 2 } \left ( \hat { y } - y \right ) ^ { 2 } = \frac { 1 } { 2 } \big ( g _ o ( a _ 1 ^ m ) - y \big ) ^ { 2 } ,$$

که $$g _ o ( x )$$ تابع فعال‌سازی لایه خروجی است.

بنابراین، با اعمال مشتق جزئی و استفاده از قاعده زنجیره‌ای، خواهیم داشت:

$$\large \delta _ 1 ^ m = \left ( g _ 0 ( a _ 1 ^ m ) - y \right ) g _ o ^ { \prime } ( a _ 1 ^ m ) = \left ( \hat { y } -y \right ) g _ o ^ { \prime } ( a _ 1 ^ m ) .$$

با قرار دادن همه این‌ها در کنار یکدیگر، مشتق جزئی تابع خطای $$E$$ نسبت به وزن لایه خروجی $$w _ { i 1 } ^ m$$ برابر خواهد بود با:

$$\large \frac { \partial E } { \partial w _ { i 1 } ^ m } = \delta _ 1 ^ m o _ i^ { m - 1 } = \left ( \hat { y } - y \right ) g _ o ^ { \prime } ( a _ 1 ^ m ) \ o _ i ^ { m - 1 } .$$

لایه‌های پنهان

اکنون این پرسش پیش می‌آید که چگونه باید مشتقات جزئی لایه‌های غیر از لایه خروجی محاسبه کرد. خوشبختانه، قاعده زنجیره‌ای برای توابع چندمتغیره نیز کارساز است. معادله زیر را برای جمله خطای $$\delta _ j ^ k$$ در لایه $$1 \le k < m$$ مشاهده کنید:

$$\large \delta _ j ^ k = \frac { \partial E } { \partial a _ j ^ k } = \sum _ { l = 1 } ^ { r ^ { k + 1 } } \frac { \partial E } { \partial a _ l ^ { k + 1 } } \frac { \partial a _ l ^ { k + 1 } }{ \partial a _ j ^ k } ,$$

که $$l$$ از $$1$$ تا $$r ^ { k + 1 }$$ (تعداد گره‌ها در لایه بعدی) است. توجه کنید با توجه به اینکه ورودی بایاس $$o _ 0 ^ k$$ متناظر با $$w _ { 0 j} ^ { k+ 1 }$$ ثابت است، مقدار آن به خروجی‌های لایه‌های قبلی بستگی ندارد و بنابراین، $$l$$ مقدار $$0$$ نمی‌گیرد.

با قرار دادن جمله $$\delta _ l ^ { k+ 1}$$، معادله زیر را داریم:

$$\large \delta _ j ^ k = \sum _ { l = 1 } ^ { r ^ { k + 1 } } \delta _ l ^ { k + 1 } \frac { \partial a _ l ^ { k + 1 } } { \partial a _ j ^ k } .$$

با یادآوری تعریف $$a _ l ^ { k + 1 }$$، می‌توان نوشت:

$$\large a _ l ^ { k + 1 } = \sum _ { j = 1 } ^ { r ^ k } w _ {j l } ^ { k + 1 } g \big ( a _ j ^ k \big ) ,$$

که $$g ( x )$$ تابع فعال‌سازی لایه‌های پنهان است:

$$\large \frac { \partial a _ l ^ { k + 1 } } { \partial a _ j ^ k } = w _ { j l } ^ { k + 1 } g ^ { \prime } \big ( a _ j ^ k \big ) .$$

با قرار دادن این رابطه در معادله بالا، معادله نهایی جمله خطای $$\delta _ j ^ k$$ در لایه‌های پنهان به دست آمده و فرمول پس انتشار نامیده می‌شود:

$$\large \delta _ j ^ k = \sum _ { l = 1 } ^ { r ^ { k + 1 } } \delta _ l ^ { k + 1 } w _ { j l } ^ { k + 1 } g ^ { \prime } \big ( a _ j ^ k \big ) = g ^ { \prime } \big ( a _ j ^ k \big ) \sum _ { l = 1 } ^ { r ^ { k + 1 } } w _ { j l } ^{ k + 1 } \delta _ l ^ { k + 1 } .$$

با قرار دادن همه این‌ها در کنار یکدیگر، مشتق جزئی تابع خطای $$E$$ نسبت به وزن در لایه‌های پنهان $$w _ { i j } ^ k$$ برای $$1 \le k < m$$ برابر است با:‌

$$\large \frac { \partial E } { \partial w _ { i j } ^ k } = \delta _ j ^ k o _ i ^ { k - 1 } = g ^ { \prime } \big ( a _ j ^ k \big ) o _ i ^ { k - 1 } \sum _ { l = 1 } ^ { r ^ { k + 1 } } w _ { j l } ^ { k + 1 } \delta _ l ^ { k + 1 } .$$

پس انتشار به عنوان محاسبه رو به عقب

این معادله چیزی است که پس انتشار نام خود را از آن می‌گیرد. یعنی خطای $$\delta _ j ^ k$$ در لایه $$k$$ به خطاهای $$\delta _ k ^ { k + 1 }$$ در لایه بعدی $$k + 1$$ وابسته است. بنابراین، خطاها از آخرین لایه به لایه اول به سمت عقب حرکت می‌کنند. تمام آنچه لازم است، محاسبه اولین جملات خطا بر اساس خروجی محاسبه شده $$\hat { y } = g _ o ( a _ 1 ^ m )$$ و خروجی هدف $$y$$ است. سپس، با اعمال یک مجموع حاصل‌ضرب (وزن‌دهی شده با $$w _ { jl} ^ {k+1}$$)، عبارات خطا برای لایه قبلی محاسبه شده و مقیاس‌بندی آن توسط $$g ^ { \prime } \big ( a _ j ^ k \big )$$ تا رسیدن به لایه ورودی تکرار می‌شود.

این انتشار خطاها به عقب بسیار شبیه به محاسبات رو به جلو است که خروجی شبکه عصبی را محاسبه می‌کند. بنابراین، محاسبه خروجی غالباً «مرحله پیش‌رو» (Forward Phase) نامیده می‌شود، در حالی که محاسبه جملات خطا و مشتقات غالباً «مرحله پس‌رو» (Backward Phase) نام دارد. در حالی که در جهت رو به جلو حرکت می‌کنیم، ورودی‌ها به طور مکرر از لایه اول به آخر با مجموع حاصل‌ضرب وابسته به وزنی $$w_ {ij} ^ k$$ بازسازی می‌شوند و توسط توابع فعال‌سازی غیرخطی $$g ( x )$$ و $$g _ o ( x )$$ تبدیل می‌شوند. در جهت عقب، «ورودی‌ها» جملات خطای لایه آخر هستند که مکرراً توسط مجموع حاصل‌ضرب وابسته به وزن $$w _ { i j } ^ k$$ از لایه آخر به حالت اول بازترکیب شده و با فاکتورهای مقیاس‌بندی غیرخطی $$g_o^{\prime}\big(a_j^m\big)$$ و $$g^{\prime}\big(a_j^k\big)$$ تبدیل می‌شوند.

علاوه بر این، از آنجا که محاسبات مرحله پس‌رو به فعال‌سازی‌های $$a _ j ^ k$$ و خروجی‌های $$o _ j ^ k$$ گره‌ها در لایه قبلی (جمله غیرخطا برای همه لایه‌ها) و بعدی (جمله خطا برای لایه‌های پنهان) وابسته‌اند، همه این مقادیر باید قبل از مرحله پس‌رو محاسبه شوند و فعال‌سازی‌های $$a _ j ^ k$$ و خروجی‌های $$o _ j ^ k$$ باید برای استفاده در مرحله پس‌رو دوباره فرا خوانده شوند. به محض اینکه مرحله پس‌رو کامل شد، و مشتقات جزئی به دست آمدند، وزن‌ها (و بایاس‌های وابسته $$b _ j ^ k  = w _{0j}^ k$$) را می‌توان با گرادیان کاهشی به‌روز کرد. این فرایند تا جایی تکرار می‌شود که یک کمینه محلی پیدا شود یا معیار همگرایی برقرار گردد.

الگوریتم پس انتشار

با استفاده از عباراتی که در بخش تعریف رسمی بیان کردیم و معادلاتی که در بخش محاسبه گرادیان‌ها به دست آوردیم، الگوریتم پس انتشار به پنج معادله زیر بستگی خواهد داشت:

• مشتق‌های جزئی:

$$\large \frac { \partial E _ d } { \partial w _ { i j } ^ k } = \delta _ j ^ k o _ i ^ { k - 1 } .$$

• خطای لایه آخر:

$$\large \delta _ 1 ^ m = g _ o ^ { \prime }( a _ 1 ^ m ) \left ( \hat { y _ d } - y _ d \right ) .$$

• خطای لایه‌های پنهان:

$$\large \delta _ j ^ k = g ^ { \prime } \big ( a _ j ^ k \big ) \sum _ { l = 1 } ^ { r ^ { k + 1 } } w _ { j l } ^ { k + 1 } \delta _ l ^ { k + 1 } .$$

• ترکیب مشتقات جزئی هر زوج ورودی-خروجی:

$$\large \frac { \partial E ( X , \theta ) } { \partial w _ { i j } ^ k } = \frac { 1 } { N } \sum _ { d = 1 } ^ N \frac { \partial }{ \partial w _ { i j } ^ k } \left ( \frac { 1 } { 2 } \left ( \hat { y _d } - y _ d \right ) ^ { 2 } \right ) = \frac { 1 }{ N } \sum _ { d = 1 } ^ N \frac { \partial E _ d } { \partial w _ { i j } ^ k } .$$

• به‌روزرسانی وزن‌ها:

$$\large \Delta w _ { i j } ^ k = - \alpha \frac { \partial E ( X , \theta ) } { \partial w _ { i j } ^ k } .$$

الگوریتم کلی

الگوریتم پس انتشار، با فرض یک نرخ بادگیری مناسب $$\alpha$$ و مقداردهی اولیه تصادفی پارامترهای $$w ^ k _ { i j }$$، در گام‌های زیر انجام می‌شود:

• (۱) فاز پیش‌رو را برای هر زوج ورودی-خروجی $$( \overrightarrow { x _ d } , y _ d )$$ محاسبه کرده و نتایج $$\hat {y _ d }$$، $$a _ j ^ k$$ و $$o _ j ^ k$$ را برای هر گره $$j$$ در لایه $$k$$ با شروع از لایه $$0$$ (لایه ورودی) تا لایه $$m$$ (لایه خروجی) ذخیره کنید.
• (۲) مرحله پس‌رو را برای هر زوج ورودی-خروجی $$( \overrightarrow { x _ d } , y _ d )$$ محاسبه کرده و نتایج $$\frac { \partial E _ d } { \partial w _ { i j } ^ k }$$ را برای هر وزن $$w _ { i j } ^ k$$ متصل کننده گره $$i$$ در لایه $$k - 1$$ به گره $$j$$ در لایه $$k$$ با پیشروی از لایه $$m$$ (لایه خروجی) به لایه $$1$$ (لایه ورودی) ذخیره کنید.
  • (الف) عبارت خطا را برای لایه نهایی $$\delta _ 1 ^ m$$ با استفاده از معادله دوم به دست آورید.
  • (ب) عبارات خطای لایه‌های پنهان $$\delta _ j ^ k$$ را به عقب برگردانید و از لایه پنهان نهایی $$k= m - 1$$ با استفاده مکرر از معادله سوم به عقب بروید.
  • (ج) مشتقات جزئی خطای جداگانه $$E_ d$$ را نسبت به $$w _ { i j } ^ k$$ با استفاده از معادله اول به دست آورید.
• (۳) گرادیان‌های جداگانه هر زوج ورودی-خروجی $$\frac { \partial E _ d } { \partial w _ { i j } ^ k }$$ را برای به دست آوردن گرادیان کل $$\frac { \partial E ( X , \theta ) } { \partial w _ { i j } ^ k }$$ برای کل مجموعه زوج‌های ورودی-خروجی $$X = \big\{ ( \overrightarrow { x _1 } , y _ 1 ) , \dots, ( \overrightarrow { x _ N } , y _ N ) \big\}$$ با استفاده از معادله چهارم (یک میانگین ساده از گرادیان‌های جداگانه) ترکیب کنید.
• (۴) وزن‌ها را بر اساس نرخ یادگیری $$\alpha$$ و گرادیان کل $$\frac { \partial E ( X , \theta ) } { \partial w _ { i j } ^ k }$$ را با استفاده از معادله پنجم (حرکت در جهت گرادیان منفی) به‌روز کنید.

پس انتشار در شبکه عصبی سیگموئید

الگوریتم کلاسیک پس انتشار برای مسائل رگرسیون با واحدهای فعال‌سازی سیگموئید طراحی شده است. در حالی که پس انتشار می‌تواند برای مسائل طبقه‌بندی و همچنین شبکه‌هایی با توابع فعال‌سازی غیرسیگموئیدی کاربرد داشته باشد، تابع سیگموئید خواص ریاضی مناسبی دارد که وقتی با یک تابع فعال‌سازی خروجی مناسب ترکیب شود، درک الگوریتم را بسیار ساده می‌کند. بنابراین، در فرمول کلاسیک، تابع فعال‌سازی برای گره‌های پنهان سیگموئید ($$g ( x ) = \sigma (x)$$) و تابع فعال‌سازی خروجی، تابع همانی ($$g _ o  ( x ) = x$$) است. خروجی شبکه فقط مقدار وزن‌داری از لایه پنهان آن، یعنی فعال‌سازی است).

پس انتشار در واقع یک عامل اصلی محرک در استفاده تاریخی از توابع فعال‌سازی سیگموئید به دلیل مشتق مناسب آن است:

$$\large g ^ { \prime } ( x ) = \frac { \partial \sigma ( x ) }{ \partial x } = \sigma ( x ) \big ( 1 - \sigma ( x ) \big ) .$$

بنابراین، محاسبه مشتق تابع سیگموئید چیزی بیش از به خاطر سپردن خروجی $$\sigma ( x )$$ و قرار دادن آن در معادله بالا نیاز ندارد.

علاوه بر این، مشتق تابع فعال‌سازی خروجی نیز بسیار ساده است:

$$\large g _ o ^ { \prime } ( x ) = \frac { \partial g _ o ( x ) }{ \partial x } = \frac { \partial x } { \partial x } = 1 .$$

بنابراین، با استفاده از این دو تابع فعال‌سازی، نیاز به یادآوری مقادیر فعال‌سازی $$a _ 1 ^ m$$ و $$a _ j ^ k$$ را علاوه بر مقادیر خروجی $$o_1^m$$ و $$o _ j ^ k$$ حذف می‌کند و باعث کاهش چشمگیر اثر حافظه الگوریتم می‌شود. این امر به این دلیل است که مشتق برای تابع فعال‌سازی سیگموئید در مرحله پس‌رو فقط باید خروجی آن تابع را در مرحله پیش‌رو به یاد بیاورد و به مقدار فعال‌سازی واقعی وابسته نیست که این مورد در فرمول عمومی‌تر پس انتشار است که $$g' (a _ j ^ k )$$ باید محاسبه شود. به طور مشابه، مشتق برای تابع فعال‌سازی همانی به چیزی وابسته نیست، زیرا یک عدد ثابت است.

بنابراین، برای یک شبکه عصبی پیش‌رو با واحدهای پنهان سیگموئید و واحد خروجی همانی، معادلات عبارت خطا به شرح زیر است:

• برای جمله خطای لایه آخر:

$$\large \delta _ 1 ^ m = \hat { y _ d } - y _ d .$$

• برای جملات خطای لایه‌های پنهان:

$$\large \delta _ j ^ k = o _ j ^ k \big ( 1 - o _ j ^ k \big ) \sum _ { l = 1 } ^ { r ^ { k + 1 } } w_ { j l} ^ { k + 1 } \delta _ l ^ { k + 1 } .$$

پیاده‌سازی روش پس انتشار در پایتون

مثال کد زیر برای یک شبکه عصبی سیگموئیدی است که در قسمت قبلی توضیح داده شد. این شبکه عصبی دارای یک لایه پنهان و یک گره خروجی است. این کد در Python3 نوشته شده است و از کتابخانه NumPy برای انجام ریاضیات ماتریسی استفاده می‌کند. از آنجا که محاسبات گرادیان برای زوج‌های ورودی-خروجی جداگانه $$( \overrightarrow { x _ d } , y _ d )$$ می‌تواند به صورت موازی انجام شود و بسیاری از محاسبات بر اساس ضرب نقطه‌ای دو بردار هستند، ماتریس‌ها راهی طبیعی برای نمایش داده‌های ورودی، داده‌های خروجی و وزن لایه را ارائه می‌دهند. محاسبات کارآمد NumPy از ضرب ماتریسی و امکان استفاده در GPUهای مدرن (که برای عملیات ماتریسی بهینه شده‌اند) می‌تواند سرعت بالایی را در هر دو مرحله رو به جلو و عقب محاسبات ارائه دهند.

فیلم آموزش پیاده سازی گام به گام شبکه های عصبی در پایتون در فرادرس

کلیک کنید

ماتریس X مجموعه ورودی‌های $$\overrightarrow {x }$$ و ماتریس y مجموعه خروجی‌های $$y$$ است. تعداد گره‌ها در لایه پنهان را می‌توان با تنظیم مقدار متغیر num_hidden سفارشی کرد. نرخ یادگیری $$\alpha$$ با متغیر alpha کنترل می‌شود. تعداد تکرارهای گرادیان کاهشی نیز با متغیر num_iterations قابل کنترل است.

با تغییر این متغیرها و مقایسه خروجی برنامه با مقادیر هدف y، می‌توان دریافت که این متغیرها چگونه یادگیری پس انتشار مجموعه داده X و y را کنترل می‌کنند. به عنوان مثال، گره‌های بیشتر در لایه پنهان و تکرار بیشتر گرادیان نزولی به طور کلی تناسب مجموعه داده‌های آموزش را بهبود می‌بخشد. با این حال، استفاده از یک نرخ یادگیری خیلی بزرگ یا خیلی کوچک، می‌تواند باعث شود که مدل به ترتیب واگرا شود یا همگرایی‌اش بسیار کند باشد.

1import numpy as np
2
3# define the sigmoid function
4def sigmoid(x, derivative=False):
5
6    if (derivative == True):
7        return x * (1 - x)
8    else:
9        return 1 / (1 + np.exp(-x))
10
11# choose a random seed for reproducible results
12np.random.seed(1)
13
14# learning rate
15alpha = .1
16
17# number of nodes in the hidden layer
18num_hidden = 3
19
20# inputs
21X = np.array([  
22    [0, 0, 1],
23    [0, 1, 1],
24    [1, 0, 0],
25    [1, 1, 0],
26    [1, 0, 1],
27    [1, 1, 1],
28])
29
30# outputs
31# x.T is the transpose of x, making this a column vector
32y = np.array([[0, 1, 0, 1, 1, 0]]).T
33
34# initialize weights randomly with mean 0 and range [-1, 1]
35# the +1 in the 1st dimension of the weight matrices is for the bias weight
36hidden_weights = 2*np.random.random((X.shape[1] + 1, num_hidden)) - 1
37output_weights = 2*np.random.random((num_hidden + 1, y.shape[1])) - 1
38
39# number of iterations of gradient descent
40num_iterations = 10000
41
42# for each iteration of gradient descent
43for i in range(num_iterations):
44
45    # forward phase
46    # np.hstack((np.ones(...), X) adds a fixed input of 1 for the bias weight
47    input_layer_outputs = np.hstack((np.ones((X.shape[0], 1)), X))
48    hidden_layer_outputs = np.hstack((np.ones((X.shape[0], 1)), sigmoid(np.dot(input_layer_outputs, hidden_weights))))
49    output_layer_outputs = np.dot(hidden_layer_outputs, output_weights)
50
51    # backward phase
52    # output layer error term
53    output_error = output_layer_outputs - y
54    # hidden layer error term
55    # [:, 1:] removes the bias term from the backpropagation
56    hidden_error = hidden_layer_outputs[:, 1:] * (1 - hidden_layer_outputs[:, 1:]) * np.dot(output_error, output_weights.T[:, 1:])
57
58    # partial derivatives
59    hidden_pd = input_layer_outputs[:, :, np.newaxis] * hidden_error[: , np.newaxis, :]
60    output_pd = hidden_layer_outputs[:, :, np.newaxis] * output_error[:, np.newaxis, :]
61
62    # average for total gradients
63    total_hidden_gradient = np.average(hidden_pd, axis=0)
64    total_output_gradient = np.average(output_pd, axis=0)
65
66    # update weights
67    hidden_weights += - alpha * total_hidden_gradient
68    output_weights += - alpha * total_output_gradient
69
70# print the final outputs of the neural network on the inputs X
71print("Output After Training: \n{}".format(output_layer_outputs))

حاصل اجرای برنامه بالا به صورت زیر است:‌

Output After Training: 
[[  2.11135662e-04]
 [  9.99525588e-01]
 [  1.66889680e-04]
 [  9.99576185e-01]
 [  9.99362960e-01]
 [  1.30185107e-03]]