تابع ناپیوسته — به زبان ساده

پیشتر در وبلاگ فرادرس مفاهیم مربوط به توابع را توضیح دادیم. از این رو در این مطلب قصد داریم تا تابع ناپیوسته و نحوه تشخیص آن را شرح دهیم.
مقدمه
اگر تابع $$ \large f \left ( x \right ) $$ در نقطه $$ \large x = a $$، پرش یا برشی داشته باشد، در نقطه مذکور ناپیوسته محسوب میشود. برای نمونه اشکال زیر دو تابع پیوسته و ناپیوسته را نشان میدهند.
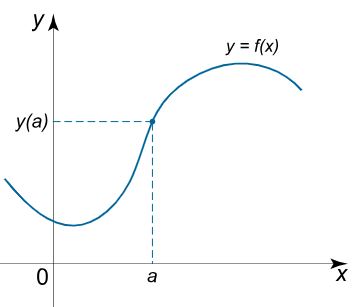
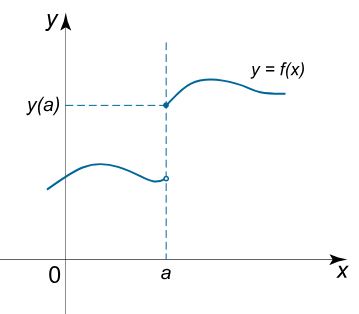
توجه داشته باشید که نوع این ناپیوستگیها متفاوت هستند. در ادامه دستهبندی توابع ناپیوسته را بیشتر توضیح میدهیم.
دستهبندی تابع ناپیوسته
معمولا در منابع، ناپیوستگی را به صورت ناپیوستگی نوع اول و دوم معرفی میکنند. یک تابع در نقطه $$ \large x= a $$ دارای ناپیوستگی اول است اگر:
- حد چپ و راست تابع در $$ \large x= a $$ موجود باشد. مقدار این حدود به ترتیب به صورتِ $$ \large \lim\limits_{x \to a ^ {– }} f\left( x \right) $$ و $$ \large \lim\limits_{x \to a ^ {+ }} f\left( x \right) $$ نشان میدهند.
- این حدود یک طرفه، عددی محدود هستند (بینهایت نمیشوند).
علاوه بر حالات فوق، شرایط زیر نیز ممکن است برقرار باشد.
- حدود چپ و راست با هم برابر باشند.
- تابع در نقطه $$ \large x= a $$ تعریف نشده باشد.
شرایط فوق حالتی را توصیف میکند که نقطه، قابل حذف باشد. این حالت از ناپیوستگی قابل رفع است. در شرایطی دیگر حد چپ و راست موجود است اما مقدار آنها با هم متفاوت است. در این حالت تابع در نقطه $$ \large x= a $$ یک ناپیوستگی را تجربه میکند.
ناپیوستگی نوع دوم زمانی وجود دارد که یکی از حدود چپ یا راست موجود نبوده یا مقدار آن بینهایت باشد. این نوع از ناپیوستگی غیر قابل حذف است بنابراین در برخی متون از آن تحت عنوان ناپیوستگی بنیادی یاد میشود.
مثال ۱
وضعیت پیوستگی تابع زیر را تعیین کنید.
$$ \large f \left ( x \right ) = { 3 ^ { \Large \frac { x } { {1 – { x ^ 2 } } } \normalsize } } $$
با توجه به مفاهیم تابع، به راحتی میتوان دریافت که تابع فوق در نقاط $$ \large x = \pm 1 $$ تعریف نشده است. بنابراین این تابع در نقاط مذکور ناپیوسته خواهد بود. به منظور تعیین نوع ناپیوستگی در ابتدا حدود یک طرفه را در نقطه $$ \large x = - 1 $$ به صورت زیر محاسبه میکنیم. در ابتدا حد چپ و راست در نقطه $$ \large \begin {align*} x = - 1 \end {align*} $$ برابر است با:
$$ \large { \lim \limits _ { x \to – 1 ^ {-}} {3^{\Large\frac{x}{{1 – {x^2}}}\normalsize}} = {3^{\Large\frac{{ – 1}}{{ 0 ^ {-}}}\normalsize}} } = { { 3 ^ \infty } = + \infty \ \ \ ,\;\;\; } \kern-0.3pt
{ \lim \limits _ { x \to – 1 ^ + } { 3 ^ { \Large \frac { x } { { 1 – { x ^ 2 } } } \normalsize}} = { 3 ^ { \Large \frac { { – 1 } } { { 0 ^ +}}\normalsize } } } = { { 3 ^ { – \infty } } = \frac { 1 } { {{ 3 ^ \infty } } } = 0 } $$
به همین صورت حدود چپ و راست در نقطه $$ \large \begin {align*} x = 1 \end {align*} $$ به صورت زیر بدست میآیند.
$$ \large \begin {align*} { \lim \limits _ { x \to 1 ^ – } { 3 ^ {\Large\frac{x}{{1 – {x^2}}}\normalsize}} = { 3 ^ { \Large \frac { { 1 } } { { 0 ^ + } } \normalsize } } }={ {3 ^ \infty } = + \infty \ \ ,\;\;\;}\kern-0.3pt
{ \lim \limits _ { x \to 1 ^ + } { 3 ^ { \Large \frac { x } { { 1 – { x ^ 2 } } } \normalsize } } = { 3 ^ { \Large \frac { { 1 } } { { 0 ^ - } } \normalsize } } } = { { 3 ^ { – \infty } } = \frac { 1 } { { { 3 ^ \infty } } } = 0 } \end {align*} $$
در هر دو نقطه حدود بینهایت وجود دارد. بنابراین ناپیوستگی از نوع دوم بوده و غیر قابل رفع خواهد بود.
مثال ۲
نقطه تابع ناپیوسته زیر از کدام نوع است.
$$ \large \begin {align*} f \left ( x \right ) = { \large \frac { { \sin x } } { x } \normalsize } \end {align*} $$
بدیهی است که تابع در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ تعریف نشده است. از طرفی میدانیم که حد تابع در این نقطه برابر است با:
$$ \large \begin {align*} f \left ( x \right ) = { \large \frac { { \sin x } } { x } \normalsize } \end {align*} $$
بنابراین ناپیوستگی تابع از نوع اول بوده و قابل رفع است. بدین منظور میتوان تابعی پیوسته به صورت زیر در نظر گرفت.
$$ \large \begin {align*} { f _ 1 } \left ( x \right ) =
\begin {cases}
\Large \frac { \sin x } { x } \normalsize & x \ne 0 \\
1 &x = 0
\end{cases}
\end {align*} $$
از این رو تابع فوق به ازای تمامی مقادیر $$x$$ پیوسته است.
مثال ۳
نقاط ناپیوسته تابع $$ \large \begin {align*} f \left( x \right) = \begin {cases} 1 – { x ^ 2 } , & x \lt 0 \\ x +2, & x \ge 0 \end {cases} \end {align*} $$ را بیابید.
تابع فوق از دو بخش تشکیل شده که در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ به یکدیگر متصل شدهاند. بنابراین به منظور بررسی ناپیوستگی باید حد تابع را در این نقطه یافت. حد چپ و راست تابع را در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ به صورت زیر محاسبه میکنیم.
$$ \large \begin {align*} {\lim\limits_{x \to 0 ^ – } f \left ( x \right ) = \lim \limits _ { x \to 0 ^ – } \left( {1 – { x ^ 2 } } \right ) = 1,\;\;\;} \kern-0.3pt
{ \lim \limits _ { x \to 0 ^ + } f \left ( x \right ) = \lim \limits _ { x \to 0 ^ – } \left( {x + 2} \right) = 2 } \end {align*} $$
حد چپ و راست برای این تابع در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ برابر نیستند. از طرفی اختلاف این دو حد برابر با ۱ است. بنابراین ناپیوستگی از نوع اول است.
مثال ۴
نقاط ناپیوستگی تابع $$ \large \begin {align*} f \left ( x \right ) = \arctan { \large \frac { 1 } { x } \normalsize } \end {align*} $$ را بیابید.
همانطور که از نمودار زیر نیز میتوان فهمید، تابع در تمامی نقاط غیر از صفر پیوسته است.
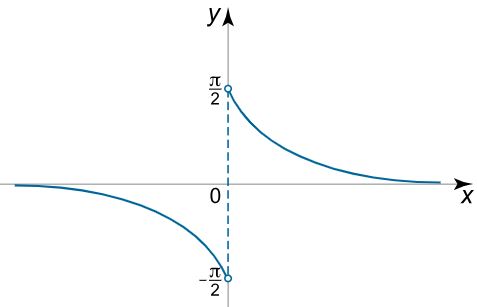
همانند مثالهای فوق، حد تابع در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ را به صورت زیر بدست میآوریم.
$$ \large \begin {align*} { \lim \limits _ { x \to 0 ^ – } \arctan \frac { 1 } { x } = \arctan \left ( { – \infty } \right ) = – \frac { \pi } { 2 } \ \ \ \ , \ \ \;\;\;}\kern-0.3pt
{\lim \limits _ { x \to 0 ^ + } \arctan \frac { 1 } { x } = \arctan \left ( { + \infty } \right) = \frac { \pi } { 2 } } \end {align*} $$
همانطور که میبینید میزان پرش تابع در نقطه $$ \large \begin {align*} x = 0 \end {align*} $$ برابر با $$ \begin {align*} \large \pi \end {align*} $$ بوده و ناپیوستگی از نوع اول است.
مثال ۵
نقاط ناپیوستگی تابع $$ \large \begin {align*} f \left ( x \right ) = { \large \frac { { \left| { 2 x + 5 } \right| } }{ { 2 x + 5 } } \normalsize } \end {align*} $$ را بیابید.
در شکل زیر نمودار این تابع ترسیم شده است.
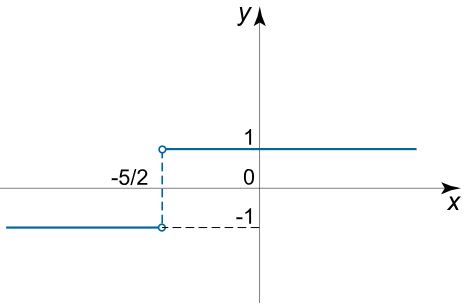
با توجه به شکل فوق میبینید که تابع در نقطه $$ \large \begin {align*} x = – { \large \frac { 5 } { 2 } \normalsize} \end {align*} $$ ناپیوسته است. بنابراین حدود چپ و راست تابع در نقطه $$ \large \begin {align*} x = – { \large \frac { 5 } { 2 } \normalsize} \end {align*} $$ برابر است با:
$$ \large \begin {align*} { \lim \limits_{x \to – \frac{5}{2} ^ – } \frac{{\left| {2x + 5} \right|}}{{2x + 5}} } = { \lim\limits_{x \to – \frac{5}{2} ^ – } \frac{{ – \left( {2x + 5} \right)}}{{2x + 5}} = – 1,\;\;\;}\kern 0.3pt {\text{if}\;\;x \lt – \frac{5}{2} } \end {align*} $$
$$\large \begin {align*} {\lim\limits_{x \to – \frac{5}{2} ^ + } \frac{{\left| {2x + 5} \right|}}{{2x + 5}} }
= {\lim\limits_{x \to – \frac{5}{2} ^ +} \frac{{ \left( {2x + 5} \right)}}{{2x + 5}} = 1,\;\;\;}\kern-0.3pt
{\text{if}\;\;x \ge – \frac{5}{2} } \end {align*} $$
همانطور که میبینید حدود چپ و راست در نقطه مذکور با هم برابر نبوده و فاصله آنها برابر با ۲ واحد است. از طرفی این حدود مقادیری محدود هستند؛ بنابراین ناپیوستگی از نوع اول محسوب میشود.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضی
- مجموعه آموزشهای ریاضی و فیزیک
- حد در ریاضی - به زبان ساده
- حد توابع چند متغیره — به زبان ساده
- پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
^^











سلام ممنون از محتوای عالیتون فقط تو حل مثالها یک مقدار کم کاری شده