نسبت سیگنال به نویز چیست؟ — از صفر تا صد

نسبت سیگنال به نویز (Signal to Noise Ratio) برابر با نسبت توان سیگنال به توان نویز موجود در آن سیگنال است که به اختصار به آن SNR میگویند. نسبت سیگنال به نویز معیاری برای بیان عملکرد بهینه سیستم پردازش سیگنال محسوب میشود، البته به شرط اینکه نویز یک تابع گاوسی (Gaussian) باشد. در این مطلب ابتدا به بیان ریاضی نسبت سیگنال به نویز و محاسبه مقدار آن در سیستمهای مختلف میپردازیم. سپس نسبت سیگنال به نویز را در یک سیگنال فرضی توسط برنامهنویسی در متلب به دست میآوریم.
نسبت سیگنال به نویز
نسبت سیگنال به نویز، سطح توان سیگنال را با سطح توان نویز مقایسه میکند و معمولا بر حسب دسیبل بیان میشود. هرچه مقدار نسبت سیگنال به نویز بیشتر باشد، برای یک سیستم مشخصه بهتری محسوب میشود؛ زیرا اطلاعات مفید بیشتری در قالب سیگنال، نسبت به اطلاعات ناخواسته یا نویز دریافت میشود.
به عنوان مثال، زمانی که یک سیگنال صوتی نسبت سیگنال به نویز برابر با ۱۰۰ دسیبل داشته باشد، به این معنی است که سطح سیگنال صوتی ۱۰۰ مرتبه از سطح سیگنال نویز در آن سیستم بالاتر است. به همین دلیل است که نسبت سیگنال به نویز ۱۰۰ نسبت به SNR برابر با ۷۰ مشخصه بهتری به حساب میآید.
در یک سیستم، سیگنال ممکن است دارای توصیف آماری یا فاقد توصیف آماری باشد، در حالی که نویز همواره توسط یک توزیع آماری توصیف میشود. زمانی که سیگنال، قطعی (Deterministic) باشد، توان آن را میتوان توسط فرمول زیر محاسبه کرد:
که در این فرمول برابر با طول بازه مشاهده (Observation) است که میتواند بینهایت نیز باشد. در حالتی که طول بازه مشاهده بینهایت باشد، باید از رابطه حد گرفته شود. برای سیگنالهای متناوب از عبارات مخصوصی استفاده میشود. در این حالت طول بازه برابر با دوره تناوب سیگنال است و مقدار مجذور میانگین مربعات (Root Mean Squared) یا rms سیگنال برابر با جذر توان آن خواهد بود. به عنوان مثال، سیگنال سینوسی دارای مقدار rms برابر با و توان برابر با است.
زمانی که سیگنال متعلق به یک فرایند تصادفی ایستا (Stationary Stochastic Process) باشد، توان آن سیگنال برابر با مقدار تابع همبستگی در مبدا خواهد بود. بنابراین میتوان نوشت:
در این فرمول، برابر با مقدار امید ریاضی سیگنال است. توان نویز به تابع همبستگی (Correlation) سیگنال وابسته است و بر اساس فرمول زیر به دست میآید:
نسبت سیگنال به نویز یا SNR را در حالت کلی به صورت زیر محاسبه میکنند.
نسبت سیگنال به نویز را برای یک متغیر تصادفی میتوان به یکی از دو روش زیر تعریف کرد:
- : در این متغیر تصادفی، سیگنال مورد نظر و ثابت است و یک متغیر تصادفی با مقدار امید ریاضی صفر در نظر گرفته میشود. در این حالت، نسبت سیگنال به نویز از رابطه محاسبه میشود که برابر با واریانس است.
- : در این متغیر ریاضی، و هر دو متغیرهای تصادفی هستند. توان یک متغیر تصادفی برابر با مقدار میانگین مربعات آن است. بنابراین توان سیگنال از رابطه به دست میآید. همیشه نویز دارای مقدار میانگین صفر است و به همین دلیل، توان آن برابر با مقدار واریانس خواهد بود. پس میتوان گفت نسبت سیگنال به نویز از رابطه زیر به دست میآید:
نویز سفید
زمانی که در سیستم نویز سفید وجود داشته باشد، تابع همبستگی به صورت محاسبه میشود. در این رابطه، تحت عنوان تابع دلتای دیراک (Dirac's Delta Function) و یا تابع ضربه (Impulse) شناخته میشود. کمیت برابر با ارتفاع طیفی (Spectral Height) نویز سفید و متناظر با مقدار ثابت طیف توان نویز در تمام فرکانسها است. توان نویز سفید بینهایت و مقدار نسبت سیگنال به نویز بر اساس روابط فوق، برابر با صفر به دست میآید. نویز سفید در حالت واقعی نمیتواند وجود داشته باشد؛ زیرا دارای توان بینهایت است. اما در تئوری، مهندسان از نویز سفید برای توصیف نویزهایی استفاده میکنند که طیف توان در آنها به خوبی در طول پهنای باند پراکنده شده باشد.
زمانی که فرض کنیم در سیستم نویز سفید وجود داشته باشد، سیستمهای پردازش سیگنال بهینه میتوانند آن را به حساب آورند و در نتیجه عملکرد آنها به یک تعریف اصلاح شده از نسبت سیگنال به نویز بستگی خواهد داشت. هنگامی که سیگنال قطعی باشد، نسبت سیگنال به نویز به صورت زیر محاسبه میشود:
پیک نسبت سیگنال به نویز
در سیستمهای پردازش تصویر (Image Processing) نسبت سیگنال به نویز تعریف متفاوتی دارد. در این حالت، صورت کسر برابر با مربع مقدار پیک سیگنال است و در مخرج کسر، توان نویز یا واریانس آن قرار میگیرد. به عنوان مثال، یک تصویر ۸ بیتی دارای مقادیر در بازه ۰ تا ۲۵۵ است. در نتیجه برای محاسبه پیک نسبت سیگنال به نویز یا PSNR، صورت در تمام موارد برابر با است.
بیان نسبت سیگنال به نویز بر حسب دسیبل
معمولا مهندسان نسبت سیگنال به نویز را بر حسب دسیبل و به صورت زیر بیان میکنند:
در سیستمهای مختلف، معمولا نسبت سیگنال به نویز در حدود ۲ (۳ دسیبل) را برابر با مرز بین SNR پایین و SNR بالا در نظر میگیرند. در کاربردهای پردازش تصویر، پیک نسبت سیگنال به نویز باید از ۲۰ دسیبل بزرگتر باشد، تا به عنوان یک تصویر با کیفیت محسوب شود.
تداخل
تمام تعاریف بالا چنین فرض میکنند که سیگنال و نویز به لحاظ آماری از یکدیگر مستقل هستند و از منابع جداگانه تولید میشوند. اما در بسیاری از کاربردها، بخشی از نویز از منابع انسانی ناشی میشود و به لحاظ آماری به سیگنال وابسته است. به عنوان مثال، یک سیگنال تلفن میتواند توسط سایر تلفنها و نویزهای دیگر دچار انحراف شود. در این حالت به سایر سیگنالها، تداخل میگویند و به جای SNR از نسبت سیگنال به تداخل یا SIR استفاده میشود. زمانی که هم نویز و هم تداخل در سیستم وجود داشته باشند، باید هر دو مشخصه نسبت سیگنال به نویز و نسبت سیگنال به تداخل برای توصیف عملکرد سیستم پردازش سیگنال مورد استفاده قرار گیرند.
نسبت سیگنال به نویز و معیار شایستگی
همان طور که گفتیم، نسبت سیگنال به نویز برابر با نسبت توان سیگنال به توان نویز در نظر گرفته میشود. این مشخصه را میتوان در نقاط مختلف سیستم به صورت زیر محاسبه کرد.
مشخصه SNR ورودی برابر با نسبت میانگین توان سیگنال مدولاسیون به میانگین توان نویز در ورودی در نظر گرفته میشود:
مشخصه SNR خروجی برابر با نسبت میانگین توان سیگنال دمدوله شده به میانگین توان نویز در خروجی است:
نسبت سیگنال به نویز یک کانال مخابراتی برابر با نسبت میانگین توان سیگنال مدولاسیون به میانگین توان نویز در پهنای باند سیگنال پیام است:
حال اگر نسبت سیگنال به نویز در ورودی را به نسبت سیگنال به نویز در خروجی تقسیم کنیم، معیار شایستگی (Figure of Merit) یا FOM یک سیستم به دست میآید. این معیار را با F نشان میدهند. این معیار میتواند عملکرد یک المان را توصیف کند.
در یک گیرنده، کانال، ورودی در نظر گرفته میشود. معیار شایستگی یک گیرنده را میتوان به صورت زیر محاسبه کرد:
نسبت سیگنال به نویز در یک سیستم AM
برای آنالیز نویز، مدل گیرنده زیر را در یک سیستم مدولاسیون دامنه یا AM در نظر بگیرید.

میدانیم که سیگنال مدوله شده دامنه برابر است با:
در مرحله بعد، میانگین توان سیگنال AM را محاسبه میکنیم.
این کار به شکل زیر انجام میشود:
میانگین توان نویز در پهنای باند توان برابر است با:
با جایگذاری این مقادیر در فرمول نسبت سیگنال به نویز کانال، به رابطه زیر میرسیم:
در رابطه بالا، برابر با توان سیگنال پیام است که از به دست میآید. همچنین، برابر با پهنای باند سیگنال پیام در نظر گرفته میشود.
معیار شایستگی در گیرنده AM
حال فرض کنید نویز میان گذر (Band Pass) مانند شکل بالا با سیگنال مدولاسیون دامنه در کانال ترکیب شود. این ترکیب در ورودی دمدولاتور AM اعمال میشود. به همین دلیل، ورودی دمدولاتور AM به صورت زیر به دست میآید:
در روابط فوق، و المانهای فاز و فاز تربیعی (Quadrature Phase) نویز هستند. خروجی دمدولاتور AM نیز همان پوش سیگنال بالا خواهد بود.
توان میانگین سیگنال دمدوله شده به صورت زیر محاسبه میشود:
توان میانگین نویز در خروجی برابر است با:
با جایگذاری این مقادیر در فرمول نسبت سیگنال به نویز خروجی، به رابطه زیر دست مییابیم:
حال با جایگذاری این مقدار در فرمول گیرنده AM داریم:
بنابراین معیار شایستگی در گیرنده AM کمتر از یک خواهد بود.
نسبت سیگنال به نویز در DSBSC
گیرنده مدل DSBSC برای آنالیز نویز را مانند تصویر زیر در نظر بگیرید.
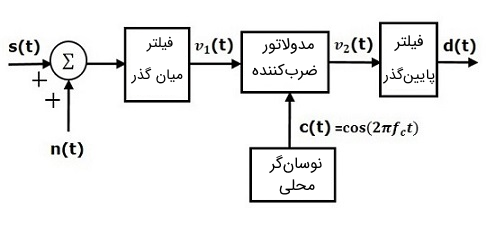
میدانیم که سیگنال مدوله شده DSBSC به صورت زیر است:
میانگین توان سیگنال مدوله شده با رابطه زیر محاسبه میشود:
میانگین توان نویز در سیگنال پیام برابر است با:
با جایگذاری این مقادیر در نسبت سیگنال به نویز کانال داریم:
معیار شایستگی گیرنده DSBSC
فرض کنید که نویز میان گذر مطابق تصویر فوق با سیگنال مدوله شده DSBSC در کانال ترکیب شود. این سیگنال ترکیبشده به عنوان یکی از ورودیها به مدولاتور ضربکننده اعمال میشود. به همین دلیل، ورودی مدولاتور ضربکننده به صورت زیر به دست میآید:
نوسانگر محلی (Local Oscillator)، سیگنال حامل را تولید میکند. این سیگنال به عنوان یک ورودی دیگر به سیستم اعمال میشود. بنابراین مدولاتور ضربکننده یک خروجی تولید میکند که حاصل ضرب و است.
حال مقادیر و را در معادله بالا جایگزین میکنیم.
در نتیجه داریم:
زمانی که سیگنال بالا به عنوان ورودی به یک فیلتر پایین گذر اعمال شود، آنگاه خروجی فیلتر پایین گذر به صورت زیر محاسبه خواهد شد:
میانگین توان سیگنال دمدوله شده برابر است با:
میانگین توان نویز در خروجی به صورت زیر است:
با جایگذاری این مقادیر در فرمول نسبت سیگنال به نویز خروجی، به رابطه زیر میرسیم:
حال با جایگذاری این مقادیر، فرمول معیار شایستگی گیرنده DSBSC به صورت زیر محاسبه میشود:
در نتیجه معیار شایستگی گیرنده DSBSC برابر با یک به دست میآید.
نسبت سیگنال به نویز در سیستم SSBSC
مدل گیرنده سیستم SSBSC برای آنالیز نویز در تصویر زیر نشان داده شده است.

میدانیم که سیگنال مدوله شده SSBSC دارای باند جانبی پایین (Lower Sideband) به صورت زیر است:
میانگین توان سیگنال مدوله شده SSBSC به صورت زیر محاسبه میشود:
میانگین توان نویز در پهنای باند پیام برابر است با:
با جایگذاری این مقادیر در فرمول نسبت سیگنال به نویز کانال، به مقادیر زیر میرسیم:
معیار شایستگی گیرنده SSBSC
فرض کنید که نویز میان گذر مانند شکل فوق، با سیگنال مدوله شده SSBSC ترکیب شود. این ترکیب به عنوان یکی از ورودیها به مدولاتور ضربکننده اعمال میشود.
به همین دلیل، ورودی مدولاتور ضربکننده به صورت زیر نوشته میشود:
نوسانگر محلی سیگنال حامل را تولید میکند. این سیگنال به عنوان یکی دیگر از ورودیها به مدولاتور ضربکننده اعمال میشود. بنابراین، مدولاتور ضربکننده یک خروجی را تولید میکند که حاصل ضرب و است.
با جایگذاری و در معادله بالا به رابطه زیر میرسیم:
زمانی که سیگنال بالا به عنوان ورودی به فیلتر پایین گذر وارد شود، آنگاه خروجی فیلتر پایین گذر برابر است با:
میانگین توان سیگنال دمدوله شده به صورت زیر به دست میآید:
میانگین توان نویز در خروجی برابر است با:
با جایگذاری این مقادیر در نسبت سیگنال به نویز خروجی، به رابطه زیر میرسیم:
بنابراین، معیار شایستگی گیرنده SSBSC برابر با یک است.
نسبت سیگنال به نویز در متلب
در این قسمت میخواهیم نحوه محاسبه نسبت سیگنال به نویز در متلب را بررسی کنیم. ابتدا دادههای خود را در فرمت mat و با نام file ذخیره و سپس با استفاده از دستور زیر آنها را بارگذاری میکنیم.
1my_data_SNR = SNR_calculation(’file’, 1.02e7, 5, .018e7, 1.2945e7);حال برنامه زیر را اجرا میکنیم.
1function SNR = calculate_SNR (filename1, fp, num_pulses, w, d)
2%% usage: SNR = calculate_SNR (filename1, fp, num_pulses, w, d)
3%%
4%% SNR, an integer variable, will be stored in your workspace for
5%% convenience of tracking SNR at different meaningful distances or
6%% circumstances surrounding the VHF beacon
7%%
8%% fp is the sample, or array index, of the first pulse
9%% num_pulses is the number of pulses seen, visually from
10%% w and d are the pulse width and time delay between pulses
11%% w and d should be an integer representing the number of samples for w and d
12
13%% plot(abs(IQ_file))
14%% after the IQ file has been read with
15%% IQ_file = read_complex_binary_gnu_radio(’IQ_data_file’)
16%%
17s_and_n = read_complex_binary (filename1); %reading IQ file
18function v = read_complex_binary (filename, count) %read IQ function
19m = nargchk (1,2,nargin);
20i f (m)
21usage (m);
22end
23i f (nargin < 2)
24count = Inf;
25end
26f = fopen (filename, ’rb’); %opening raw binary file
27i f (f < 0) %checking for data
28v = 0;
29e lse
30t = fread (f, [2, count], ’float’); %reading as a f loat
31fclose (f); %closing file
32v = t(1,:) + t(2,:)*i; %assuming IQIQIQ structure of binary file
33[r, c] = size (v); %creating matrix to match IQ file size
34v = reshape (v, c, r); %reshaping matrix to correct format
35end
36end
37n_samples = length(abs(signal_and_noise)); %number of samples in stream
38p_noise = 0; %initializing variable p_noise (Noise Power)
39p_signal = 0; %initializing variable p_signal (Signal Power)
40for n = 0:1:num_pulses
41switch n
42case 0 %formula needed when calculating p_noise for first section
43p_noise = p_noise + mean(abs(s_and_n(1:fp)));
44p_signal = p_signal + mean(abs(s_and_n(fp + (n * 1.295e7):fp + w + (n * d))));
45case (n > 0) && (n ~= num_pulses)
46p_noise = p_noise + mean(abs(s_and_n(fp + w + ((n-1) * d):fp + w + ((n)*d))));
47p_signal = p_signal + mean(abs(s_and_n(fp + (n * d):fp + w + (n * d))));
48case num_pulses
49p_noise = p_noise + mean(abs(s_and_n(fp + w + ((n-1) * d):n_samples)));
50p_signal = p_signal + mean(abs(s_and_n(fp + ((n-1) * d):fp + w + ((n-1)*d))));
51end
52end
53p_signal = p_signal/num_pulses; %taking average power of signal
54p_noise = p_noise/(num_pulses + 1); %taking average power of noise
55p_signal = p_signal - p_noise; %subtracting avg noise power from avg signal power
56%variable to be returned to variable calling function
57SNR = 20 * log10(p_signal/p_noise); %SNR calculation, 20 comes from P = V^2/R
58%code for plotting IQ file with marked pulses
59
60plot(abs(signal_and_noise)) %plot IQ_file
61title(’Signal Inlab (w/o LNA)’) %plot title
62ylabel(’Amplitude (V)’) %y-axis label
63xlabel(’Samples @10Msps’) %x-axis label
64legend([’SNR = ’ num2str(SNR) ’ (dB)’]) %legend to display SNR
65hold on
66for n = 0:1:num_pulses
67switch n
68case 0
69plot(first_pulse, .02, ’r-o’);
70plot(first_pulse + (n * 1.295e7), .02, ’r-o’);
71case num_pulses
72plot(first_pulse + .2e6 + ((n-1) * 1.295e7), .02, ’r-o’);
73plot(first_pulse + ((n-1) * 1.295e7), .02, ’r-o’);
74otherwise
75plot(first_pulse + .2e6 + ((n-1) * 1.295e7), .02, ’r-o’);
76plot(first_pulse + (n * 1.295e7), .02, ’r-o’);
77end
78end
79hold off
80endبرای یک مجموعه داده فرضی، نمودار زیر در خروجی این برنامه ترسیم میشود.
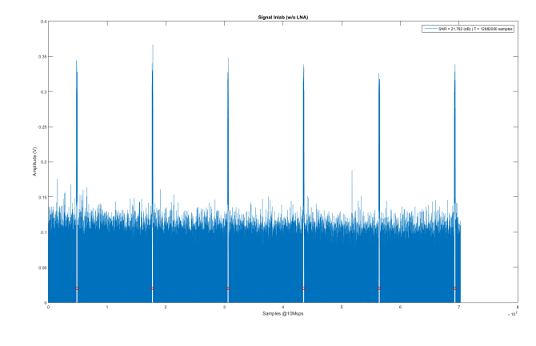
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- مدولاسیون فرکانس — از صفر تا صد
- مدولاسیون فاز — راهنمای جامع
- انرژی و توان سیگنال — از صفر تا صد
^^













عالی بود.
با تشکر از خانم مهندس