مشتق Cos – به زبان ساده + اثبات، مثال و تمرین
مشتق Cos برابر با منفی Sin است. این مشتق، شیب خط مماس بر منحنی تابع کسینوس در یک نقطه مشخص را نمایش میدهد. در سادهترین حالت، مشتق کسینوس ایکس برابر با سینوس ایکس میشود. البته مشتق تابع Cos همیشه به این صورت نیست. مشتقگیری از کسینوس چندجملهای، کسینوس تواندار، ضرب کسینوس، تقسیم کسینوس، کسینوس وارون، کسینوس هیپربولیک و غیره، روشها و فرمولهای مختص خود را دارد که در این آموزش از مجله فرادرس به معرفی آنها و حل چند مثال و تمرین مرتبط خواهیم پرداخت.
در این مطلب ابتدا مشتق کسینوس را تعریف میکنیم و فرمول آن را یاد میگیریم. در ادامه، فرمول محاسبه مشتق کسینوس را با فرمول مشتق زنجیرهای بررسی میکنیم. سپس مشتق معکوس کسینوس را یاد میگیریم و در انتها با مشتق کسینوس هیپربولیک آشنا میشویم و تمرینهایی مرتبط را نیز حل میکنیم. پس اگر میخواهید به طور کامل با مشتق کسینوس آشنا شوید، تا انتهای این مطلب از مجله فرادرس همراه باشید.
مشتق توابع مثلثاتی چیست؟
مشتق، یکی از پرکاربردترین مفاهیم ریاضی است که معمولا به منظور تعیین نرخ تغییرات پارامترهای مختلف در حوزههای مختلفی نظیر علوم مهندسی، علوم پایه، علوم اقتصادی مورد استفاده قرار میگیرد.
این مفهوم، به صورت شیب خط مماس بر نمودار در یک نقطه مشخص تعریف میشود. بنابراین، مشتق توابع مثلثاتی، رابطه شیب خط مماس بر نمودار این توابع را در نمایش میدهد. جدول زیر، حاوی رابطه مشتق سادهترین فرم توابع مثلثاتی است.
| عنوان تابع مثلثاتی | رابطه تابع مثلثاتی | مشتق تابع مثلثاتی |
| سینوس | $$ \sin ( x ) $$ | $$ \cos ( x ) $$ |
| کسینوس | $$ \cos ( x ) $$ | $$ - \sin ( x ) $$ |
| تانژانت | $$ \tan ( x ) $$ | $$ \sec ^ ۲ ( x ) $$ |
| کتانژانت | $$ \cot ( x ) $$ | $$ - \csc ^ ۲ ( x ) $$ |
| سکانت | $$ \sec ( x ) $$ | $$ \sec ( x ) \ \tan ( x ) $$ |
| کسکانت | $$ \cos ( x ) $$ | $$ - \csc ( x ) \ \cot ( x ) $$ |
مشتق COS چیست؟
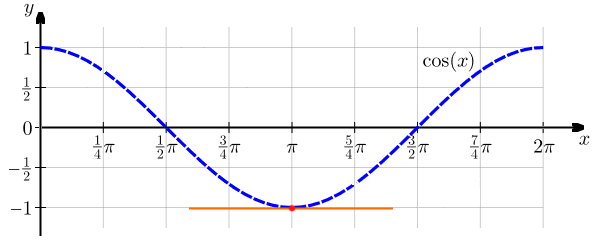
مشتق کسینوس، شیب خط مماس بر نمودار تابع کسینوس در یک نقطه مشخص است. به عنوان مثال، تصویر زیر، خط مماس بر نمودار تابع $$ \cos ( x ) $$ را در نقطه $$ x = \pi $$ (زاویه ۱۸۰ درجه) نمایش میدهد.
این خط مماس، به صورت افقی بوده و دارای شیب ۰ است. بنابراین و بر اساس تعریف، مشتق کسینوس در زاویه ۱۸۰ درجه برابر با ۰ میشود.
مشتق Cos یک زاویه با Sin- همان زاویه برابری میکند. فرمول مشتق Cos به صورت زیر نوشته میشود:
$$ \frac { d } { d x } [ \cos ( x ) ] = - \sin( x ) $$
$$ \cos ^ { \prime } ( x ) = - \sin ( x ) $$
به این ترتیب، اگر بخواهیم شیب خط مماس بر نمودار تابع کسینوس را در یک زاویه مشخص به دست بیاوریم، کافی است مقدار سینوس آن زاویه را تعیین کنیم.
مثال ۱: مشتق Cos x
در این مثال، میخواهیم مشتق $$ \cos ( x ) $$ را با فرض $$ x = ۳۰ ^ { \circ } $$ به دست بیاوریم. به این منظور، ابتدا فرمول جبری مشتق کسینوس را مینویسیم. این فرمول عبارت است از:
$$ \frac { d } { d x } [ \cos ( x ) ] = - \sin( x ) $$
سپس، زاویه ۳۰ درجه را به جای $$ x $$ درون رابطه بالا جایگذاری میکنیم:
$$
\frac { d } { d x } [ \cos ( ۳۰ ^ { \circ } ) ] = - \sin( ۳۰ ^ { \circ })
$$
اگر با مقادیر سینوس در زوایای معروف آشنایی داشته باشید، حتما میدانید که سینوس زاویه ۳۰ درجه برابر با $$ \frac { ۱ } { ۲ } $$ (یکدوم) یا همان $$ ۰/۵ $$ (نیم) است. بنابراین، داریم:
$$
\frac { d } { d x } [ \cos ( ۳۰ ^ { \circ } ) ] = - \frac { ۱ } { ۲ }
$$
به عبارت دیگر، مشتق کسینوس سی درجه با یکدوم برابری میکند.
فرمول مشتق Cos چیست؟
فرمول مشتق Cos، به عبارت داخل تابع کسینوس بستگی دارد. در سادهترین حالت، این فرمول به صورت زیر نوشته میشود:
$$ \frac { d } { d x } [ \cos ( x ) ] = - \sin( x ) $$
اگر عبارت درون تابع کسینوس، تابعی مانند u باشد، فرمول مشتق به شکل زیر درمیآید:
$$
\frac { d } { d x } [ \cos ( u ) ] = - u ^ { \prime } \sin( u )
$$
مثال ۲: مشتق Cos u
تابع $$ \cos ( u ) $$ را در نظر بگیرید. قصد داریم مشتق این تابع را با فرض $$ u = x ^ ۲ $$ تعیین کنیم. از آنجایی $$ u $$، تابعی از $$ x $$ است، مشتق $$ \cos ( u ) $$ بر اساس رابطه زیر به دست میآید:
$$
\frac { d } { d x } [ \cos ( u ) ] = - u ^ { \prime } \sin( u )
$$
برای تعیین مشتق $$ \cos ( u ) $$، به مشتق $$ u $$ نیاز داریم. این مشتق با استفاده فرمولهای مشتق توابع چندجملهای به دست میآید. به این ترتیب، داریم:
$$
\frac { d } { d x } u = \frac { d } { d x } x ^ ۲ = ۲ x
$$
این جواب را درون رابطه مشتق Cos u قرار میدهیم:
$$
\frac { d } { d x } [ \cos ( x ^ ۲ ) ] = - ۲ x \sin( x ^ ۲ )
$$
محاسبه مشتق Cos با فرمول مشتق زنجیره ای
فرمولی که برای مشتق Cos u معرفی کردیم، با عنوان رابطه مشتق زنجیرهای شناخته میشود. این رابطه برای مشتقگیری از توابع تو در تو مورد استفاده قرار میگیرد.
به عنوان مثال، بر اساس قاعده زنجیرهای، مشتق تابع $$ f [ g ( x ) ] $$ عبارت است از:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$

مثال ۳: مشتق Cos ۲x
در این مثال قصد داریم مشتق تابع $$ \cos ( ۲ x ) $$ را به دست بیاوریم. $$ \cos ( ۲ x ) $$، یک تابع تو در تو است. بنابراین، برای تعیین مشتق آن میتوانیم از قاعده زنجیرهای کمک بگیریم. بر اساس این قاعده، داریم:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
اکنون، تغییر متغیرهای زیر را در نظر بگیرید:
$$ f ( x ) = \cos ( x ) $$
$$ g ( x ) = ۲ x $$
برای استفاده از فرمول مشتق زنجیرهای، علاوه بر تغییر متغیرهای بالا، به مشتقهای زیر نیز نیاز داریم:
$$ f ^ { \prime } ( x ) = \cos ^ { \prime } ( x ) = - \sin ( x ) $$
$$ g ^ { \prime } ( x ) = ( ۲ x ) ^ { \prime } = ۲ $$
$$
f ^ { \prime } [ g ( x ) ] = \cos ^ { \prime } ( ۲x ) = - \sin ( ۲ x )
$$
به این ترتیب، داریم:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
$$
\frac { d } { d x } \cos ( ۲ x ) = - \sin ( ۲ x ) \times ۲
$$
$$
\frac { d } { d x } \cos ( ۲ x ) = - ۲ \sin ( ۲ x )
$$
مثال ۴: مشتق Cos^۲
برای به دست آوردن مشتق $$ \cos ^ ۲ ( x ) $$، دو راه کلی داریم. یکی از این راهها، استفاده از قاعده زنجیرهای در مشتقگیری و راه دیگر، کمک گرفتن از فرمول مشتق ضرب دو تابع است. در اینجا، از قاعده مشتق زنجیرهای استفاده میکنیم. این قاعده به صورت زیر نوشته میشود:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
برای درک نحوه استفاده از رابطه بالا به منظور تعیین مشتق کسینوسهای تواندار (مانند این مثال)، تغییر متغیرهای زیر را در نظر بگیرید:
$$ f ( x ) = x ^ ۲ $$
$$ g ( x ) = \cos ( x ) $$
به این ترتیب، داریم:
$$ f [ g ( x ) ] = g ^ ۲ ( x ) $$
$$ f [ \cos ( x ) ] = \cos ^ ۲ ( x ) $$
اکنون، مشتق توابع $$ f ( x ) $$ و $$ g ( x ) $$ را به دست میآوریم:
$$ f ^ { \prime } ( x ) = ( x ^ ۲ ) ^ { \prime } = ۲ x $$
$$ g ^ { \prime } ( x ) = \cos ^ { \prime } ( x ) = - \sin ( x ) $$
علاوه بر این موارد، به مشتق $$ f [ g ( x ) ] $$ نیز نیاز داریم. این مشتق عبارت است از:
$$
f ' [ g ( x ) ] = ۲ g ( x ) = ۲ \cos ( x )
$$
تمام پارامترهای تعیین شده را درون رابطه مشتق زنجیرهای قرار میدهیم:
$$
\frac { d } { d x } f \left [ g ( x ) \right ] = f ' [ g ( x ) ] g ' ( x )
$$
$$
\frac { d } { d x } \cos ^ ۲ ( x ) = ۲ \cos ( x ) \times [ - \sin ( x ) ]
$$
$$
\frac { d } { d x } \cos ^ ۲ ( x ) = - ۲ \cos ( x ) \sin ( x )
$$
$$
\frac { d } { d x } \cos ^ ۲ ( x ) = - \sin ( ۲ x )
$$
برای بیان مشتق Cos^۲، همان از جواب بالا و هم از جواب قبلی آن استفاده میشود؛ چراکه بر اساس قوانین مثلثات، داریم:
$$ ۲ \cos ( x ) \sin ( x ) = \sin ( ۲ x ) $$
مشتقگیری به روش زنجیرهای، کاربرد بسیار زیادی در به دست آوردن مشتق انواع توابع ریاضی، از جمله توابع مثلثاتی دارد. اگر برای این مثال از فرمول مشتق ضرب دو تابع استفاده میکردیم، شاید درک فرآیند حل سادهتر میشد. با این وجود، اگر توان Cos بالاتر میبود، قطعا توسط روش زنجیرهای، با سرعت بیشتری به جواب میرسیدیم. این موضوع را در تمرین ۲ از بخش «حل تمرین مشتق Cos» مورد بررسی قرار میدهیم.
مشتق معکوس Cos
مشتق تابع وارون Cos یا همان $$ \arccos ( x ) $$ برابر است با:
$$ \frac { d } { d x } \arccos ^ { - ۱ } ( x ) = - \frac { ۱ }{ \sqrt { ۱ - x ^ ۲ } } $$
$$ \arccos ( x ) $$ به صورت $$ \cos ^ { - ۱ } ( x ) $$ نوشته میشود. اگر به جای $$ x $$، تابعی مانند $$ u $$ در وارون کسینوس قرار داشته باشد، رابطه بالا به شکل زیر تغییر میکند:
$$
\frac { d } { d x } \cos ^ { - ۱ } ( u ) = - \frac { u ^ { \prime } }{ \sqrt { ۱ - u ^ ۲ } }
$$

مثال ۴: مشتق Cos اینورس
در این مثال میخواهیم مشتق تابع $$ \arccos ( x ^ ۲ + ۷ x ) $$ را به دست بیاوریم. به این منظور، از رابطه کلی مشتق Cos اینورس استفاده میکنیم. این رابطه به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \arccos ( u ) = - \frac { u ^ { \prime } }{ \sqrt { ۱ - u ^ ۲ } }
$$
در رابطه بالا میتوانیم $$ u $$ را برابر با عبارت درون وارون کسینوس قرار دهیم:
$$ u = x ^ ۲ + ۷ x $$
به این ترتیب، برای $$ u ^ { \prime } $$، داریم:
$$ u ^ { \prime } = ۲ x + ۷ $$
در نتیجه:
$$
\frac { d } { d x } \arccos ( x ^ ۲ + ۷ x ) = - \frac { ۲ x + ۷ }{ \sqrt { ۱ - \left ( x ^ ۲ + ۷ x \right ) ^ ۲ } }
$$
مشتق Cos هیپربولیک
کسینوس هیپربولیک (Cos h)، تابعی هذلولی است که بر اساس عدد اویلر و با فرم نمایی نوشته میشود:
$$ \cosh ( x ) = \frac { e ^ x + e ^ { - x } }{ ۲ } $$
مشتق Cos h برابر است با:
$$ \frac { d } { d x } \cosh ( x ) = \frac { e ^ x - e ^ { - x } }{ ۲ } $$
عبارت کسری در سمت راست رابطه مشتق کسینوس هیپربولیک، معادل سینوس هیپربولیک است. به عبارت دیگر، مشتق Cos h با Sin h برابری میکند:
$$ \frac { d } { d x } \cosh ( x ) = \sinh ( x ) $$
در حالت کلی، رابطه کسینوس هیپربولیک به صورت زیر نوشته میشود:
$$ \frac { d } { d x } \cosh ^ { - ۱ } [ u ( x ) ] = \frac { u ^ { \prime } ( x ) }{ \sqrt { u ^ ۲ ( x ) - ۱ } } $$
حل تمرین مشتق Cos
در این بخش، به منظور آشنایی بیشتر و بهتر با نحوه حل مسائل مرتبط با مشتق Cos، چندین تمرین متنوع را مورد بررسی قرار میدهیم.
تمرین ۱: اثبات مشتق Cos x
مشتق تابع $$ \cos ( x ) $$ برابر با $$ - \sin ( x ) $$ است. این رابطه را اثبات کنید.
صورت سوال، اثبات رابطه زیر را از ما میخواهد:
$$ \frac { d } { d x } [ \cos ( x ) ] = - \sin( x ) $$
روشهای مختلفی برای اثبات مشتق Cos x وجود دارد که از معروفترین آنها میتوان به استفاده از تعریف حدی مشتق، قاعده مشتق زنجیرهای و فرمول مشتق تقسیم کرد. در اینجا، رابطه مورد سوال را توسط تعریف حدی مشتق اثبات میکنیم. بر اساس این تعریف، مشتق تابع $$ f ( x ) $$ در نقطه $$ x $$ برابر با حاصل حد زیر است:
$$ f ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } $$
بنابراین، اگر $$ f ( x ) $$ را برابر با $$ \cos ( x ) $$ در نظر بگیریم، خواهیم داشت:
$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x + \Delta x ) - \cos ( x ) } { \Delta x }
$$
بر اساس قوانین مثلثات، داریم:
$$
\cos ( x + \Delta x ) = \cos ( x ) \cos ( \Delta x ) − \sin ( x ) \sin ( \Delta x )
$$
اکنون، این رابطه را درون حد قرار میدهیم و عبارتهای موجود را به صورت زیر ساده میکنیم:
$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x ) \cos ( \Delta x ) − \sin ( x ) \sin ( \Delta x ) - \cos ( x ) } { \Delta x }
$$
$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x ) \cos ( \Delta x ) - \cos ( x ) } { \Delta x } - \lim _ { \Delta x \to ۰ } \frac { \sin ( x ) \sin ( \Delta x ) } { \Delta x }
$$
$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( \Delta x ) - ۱} { \Delta x } \cos ( x ) - \lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } \sin ( x )
$$
بر اساس قوانین حد در توابع مثلثاتی، داریم:
$$
\lim _ { \Delta x \to ۰ } \frac { \cos ( \Delta x ) - ۱} { \Delta x } = ۰
$$
$$
\lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } = ۱
$$
در نتیجه:
$$
\cos ^ { \prime } ( x ) = ۰ \times \cos ( x ) - ۱ \times \sin ( x )
$$
$$
\cos ^ { \prime } ( x ) = ۰ - \sin ( x )
$$
$$
\cos ^ { \prime } ( x ) = - \sin ( x )
$$
روشهای مختلف اثبات فرمول مشتق Cos اینورس را به طور کامل در مطلب «مشتق کسینوس – اثبات و فرمول + مثال و تمرین» توضیح دادهایم.

تمرین ۲: تعیین مشتق Cos^۳ x
مشتق تابع $$ \cos ^ ۳ ( x ) $$ را به دست بیاورید.
مشتق توابع مثلثاتی تواندار، معمولا با استفاده از قاعده زنجیرهای تعیین میشود. به این ترتیب، برای تعیین مشتق تابع کسینوس به توان ۳، ابتدا فرمول قاعده مذکور را مینویسیم:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
سپس، تغییر متغیرهای زیر را در نظر میگیریم:
$$ f ( x ) = x ^ ۳ $$
$$ g ( x ) = \cos ( x ) $$
بنابراین:
$$ f [ g ( x ) ] = \cos ^ ۳ ( x ) $$
با توجه به تغییر متغیرهای بالا، مشتقهای مورد نیاز را به دست میآوریم:
$$ f ^ { \prime } ( x ) = ۳ x ^ ۲ $$
$$ g ^ { \prime } ( x ) = - \sin ( x ) $$
$$ f ^ { \prime } [ g ( x ) ] = ۳ \cos ^ ۲ ( x ) $$
اکنون، پارامترهای به دست آمده را درون رابطه مشتق زنجیرهای قرار میهیم:
$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
$$
\frac { d } { d x } \cos ^ ۳ ( x ) = ۳ \cos ^ ۲ ( x )\left [ - \sin ( x ) \right ]
$$
$$
\frac { d } { d x } \cos ^ ۳ ( x ) = - ۳ \cos ^ ۲ ( x ) \sin ( x )
$$
تمرین ۳: مشتق تقسیم Cos
مشتق تابع $$ f ( x ) = \frac { ۱ - x ^ ۲ }{ \cos ( \frac { x }{ ۲ } ) } $$ را به دست بیاورید.
تابع مورد سوال، یک تابع کسری است، با صورت چندجملهای و مخرج کسینوس است. مشتق این تابع از رابطه مشتق تقسیم به دست میآید. بر اساس این رابطه، داریم:
$$
\left ( \frac { u ( x ) }{ v ( x ) }\right ) ^ { \prime }= \frac { u ^ { \prime } ( x ) v ( x ) – v ^ { \prime } ( x ) u ( x ) }{ u ^ ۲ ( x ) }
$$
به این ترتیب، صورت تابع مورد سوال را برابر با $$ u ( x ) $$ و مخرج آن را برابر با $$ v ( x ) $$ قرار میدهیم:
$$ u ( x ) = ۱ - x ^ ۲ $$
$$ v ( x ) = \cos ( \frac { x }{ ۲ } ) $$
سپس، از دو تابع بالا مشتق میگیریم:
$$ u ^ { \prime } ( x ) = - ۲ x $$
$$
v ^ { \prime } ( x ) = \left ( \frac { x }{ ۲ } \right ) ^ { \prime } \left [ - \sin \left ( \frac { x }{ ۲ } \right )\right ] = - \frac { ۱ } { ۲ } \sin \left ( \frac { x }{ ۲ } \right )
$$
اکنون، توابع و مشتقهایشان را درون فرمول مشتق تقسیم دو تابع جایگذاری میکنیم:
$$
\left ( \frac { ۱ - x ^ ۲ }{ \cos \left ( \frac { x }{ ۲ } \right ) } \right ) ^ { \prime }= \frac { - ۲ x \cos \left ( \frac { x }{ ۲ } \right ) – \left [ - \frac { ۱ } { ۲ } \sin \left ( \frac { x }{ ۲ } \right ) \left ( ۱ - x ^ ۲\right ) \right ]}{ \cos ^ ۲ \left ( \frac { x }{ ۲ } \right )}
$$
در نتیجه:
$$
f ^ { \prime } ( x ) = \left ( \frac { ۱ - x ^ ۲ }{ \cos \left ( \frac { x }{ ۲ } \right ) } \right ) ^ { \prime }= \frac { - ۲ x \cos \left ( \frac { x }{ ۲ } \right ) + \frac { ۱ } { ۲ } \sin \left ( \frac { x }{ ۲ } \right ) \left ( ۱ - x ^ ۲\right ) }{ \cos ^ ۲ \left ( \frac { x }{ ۲ } \right )}
$$
سوالات متداول در رابطه با مشتق Cos
در این بخش، به برخی از پرتکرارترین سوالات در رابطه مشتق Cos به طور مختصر پاسخ میدهیم.
تعریف مشتق Cos چیست؟
مشتق Cos، به صورت شیب خط مماس بر نمودار تابع Cos تعریف میشود.
رابطه مشتق Cos چیست؟
رابطه مشتق Cos، به صورت Cos'=-Sin نوشته میشود.
مشتق Cos x چیست؟
مشتق Cos x، برابر با Sin x- است.
مشتق Cos u چیست؟
مشتق Cos u، برابر با u'Sin u- است.
مشتق Cos ۲x چیست؟
مشتق Cos ۲x، برابر با ۲Sin ۲x- است.
مشتق Cos به توان ۲ چیست؟
مشتق Cos به توان ۲، برابر با Sin ۲x- است.
مشتق Cos اینورس چیست؟
مشتق Cos اینورس، برابر با منفی یک بر روی رادیکال یک منهای ایکس دو است.
مشتق Cos h چیست؟
مشتق Cos h، برابر با Sin h است.










