مدل ریاضی کانال مخابراتی – راهنمای جامع

در طراحی سیستم‌های مخابراتی برای انتقال اطلاعات از طریق کانال‌های مخابراتی فیزیکی، به دست آوردن یک مدل ریاضی از کانال (Mathematical Model for the Communication Channel) امری بسیار مفید است. مدل ریاضی کانال باید این توانایی را داشته باشد که مهم‌ترین مشخصه‌های واسط انتقال را نشان دهد و در خود منعکس کند. از مدل ریاضی کانال در طراحی انکودر کانال و نیز مدولاتور در سمت فرستنده و دیکودر کانال و دمدولاتور در سمت فرستنده نیز استفاده می‌شود. در ادامه قصد داریم مدل ریاضی کانال را به دست آوریم. از این مدل برای توصیف بسیاری از کانال‌های فیزیکی استفاده می‌شود که در عمل با آن‌ها روبه‌رو هستیم. در حالت کلی سه مدل ریاضی برای توصیف کانال‌های مخابراتی وجود دارد.

مدل ریاضی کانال نویز جمع شونده

می‌توان گفت ساده‌ترین مدل برای یک کانال مخابراتی، مدل «کانال نویز جمع شونده» (Additive Noise Channel) است.

نمایی از بلوک دیاگرام مدل ریاضی کانال نویز جمع شونده در تصویر زیر نشان داده شده است.

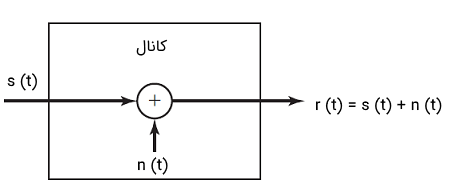
در این مدل، سیگنال ارسالی $$s ( t )$$ توسط فرایند نویز تصادفی جمع شونده $$n ( t )$$ خراب می‌شود. در حالت فیزیکی، فرایند نویز جمع شونده می‌تواند از قطعات الکترونیکی و تقویت کننده‌ها موجود در گیرنده سیستم مخابراتی نشأت بگیرد و یا مانند انتقال امواج رادیویی، به دلیل تداخلاتی به وجود بیاید که در طول مخابره وجود دارند. اگر نویز به وسیله قطعات الکترونیکی و تقویت کننده‌های موجود در گیرنده به سیگنال افزوده شود، در این حالت می‌توان آن را با «نویز حرارتی» (Thermal Noize) توصیف کرد. این نوع نویز از لحاظ آماری به عنوان یک فرایند نویز گاوسی توصیف می‌شود. به همین دلیل به مدل ریاضی کانال که به دست می‌آید، «کانال نویز گاوسی جمع شونده» (Additive Gaussian Noise Channel) می‌گویند.

به دلیل اینکه مدل کانال نویز گاوسی جمع شونده به کلاس وسیعی از کانال‌های مخابراتی فیزیکی قابل اعمال است و نیز به دلیل سادگی ریاضیاتی آن، به عنوان غالب‌ترین مدل ریاضی کانال شناخته می‌شود که در طراحی‌ و آنالیز سیستم‌های مخابراتی معمولا از آن استفاده می‌شود. تضعیف کانال نیز به سادگی در این مدل گنجانده می‌شود. زمانی که سیگنال در طول فرایند انتقال از طریق کانال مخابراتی تضعیف شود، سیگنال دریافت شده را می‌توان به صورت زیر نوشت:

$$r ( t ) = a s ( t ) + n ( t )$$

که در این فرمول $$a$$ نشان دهنده فاکتور تضعیف است.

مدل کانال فیلتر خطی

در برخی کانال‌های فیزیکی مانند کانال‌های تلفن بی‌سیم، از فیلترها استفاده می‌شود تا سیگنال‌های ارسال شده از محدوده پهنای باند خاصی تجاوز نکنند و در نتیجه با سایر سیگنال‌ها تداخل نداشته باشند. این چنین کانال‌هایی را معمولا با مدل ریاضی «کانال فیلتر خطی» (Linear Filter Channel) با نویز جمع شونده توصیف می‌کنند.

فیلم آموزش مبانی سیستم های مخابراتی‎ در فرادرس

کلیک کنید

بلوک دیاگرام مدل کانال فیلتر خطی با نویز جمع شونده در تصویر زیر نشان داده شده است.

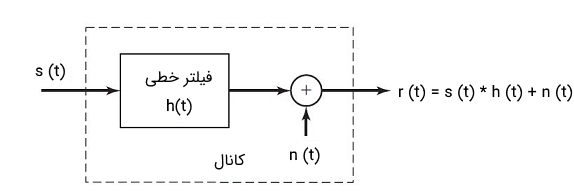
در مدل کانال فیلتر خطی با نویز جمع شونده، اگر ورودی کانال سیگنال $$s ( t )$$ باشد، در این صورت سیگنال خروجی از کانال به صورت زیر است:

$$r ( t ) = s ( t ) * h ( t ) + n ( t ) = \\ \int _ { − ∞ } ^ { + ∞ } h ( \tau ) s ( t − \tau ) d \tau + n ( t )$$

در این رابطه $$h ( t )$$ برابر با پاسخ ضربه فیلتر خطی و * نماد عمل کانولوشن در نظر گرفته می‌شود.

مدل کانال فیلتر خطی متغیر با زمان

کانال‌های فیزیکی مانند کانال‌های آکوستیک زیرآبی و کانال‌های رادیویی یونوسفر که موجب انتشار چند مسیری متغیر با زمان سیگنال ارسالی می‌شوند را می‌توان به صورت ریاضی با «فیلترهای خطی متغیر با زمان» (Time Variant Linear Filters) توصیف کرد. این فیلترهای خطی با پاسخ ضربه کانال متغیر با زمان $$h ( \tau ; t )$$ توصیف می‌شوند که $$h ( \tau ; t )$$ برابر با پاسخ کانال در زمان t بر اثر یک ضربه است که در زمان $$t − \tau$$ اعمال شده است. بنابراین $$\tau$$ نشان دهنده متغیر زمان سپری شده است.

مدل کانال فیلتر خطی متغیر با زمان با نویز جمع شونده در تصویر زیر نشان داده شده است.

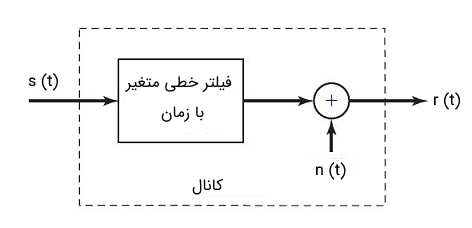
برای یک سیگنال $$s ( t )$$ سیگنال خروجی کانال به صورت زیر نوشته می‌شود:

$$r ( t ) = s ( t )* h ( \tau ; t ) + n ( t ) = \\ \int _ { − ∞ } ^ { + ∞ } h ( \tau ; t ) s ( t − \tau ) d \tau + n ( t$$

یک مدل ریاضی خوب برای انتشار چند مسیری سیگنال در کانال‌های فیزیکی مانند یونوسفر (در فرکانس‌های زیر ۳۰ مگا هرتز) و کانال‌های رادیویی سلولی موبایل، یک حالت خاص از معادله بالا است که در آن پاسخ ضربه متغیر با زمان دارای فرم زیر است:

$$h ( \tau ; t ) = \sum_ { k = 1 } ^ L a _ k ( t ) \delta ( \tau - \tau _ k )$$

در این رابطه، $$a _ k ( t )$$ نشان دهنده فاکتور تضعیف متغیر با زمان برای L مسیر انتشار چند مسیره است. اگر معادله بالا را در معادله قبل از آن جایگذاری کنیم، آن‌گاه سیگنال دریافت شده را می‌توان به صورت زیر به دست آورد:

$$r ( t ) = \sum_ { k = 1 } ^ L a _ k ( t ) s ( t − \tau ) + n ( t )$$

مشاهده می‌کنیم که سیگنال دریافت شده از L مولفه چند مسیری تشکیل شده است که هر مولفه توسط فاکتور $$a _ k$$ تضعیف و توسط فاکتور $$\tau _ k$$ تاخیر یافته است.

سه مدل ریاضی کانال که در بالا به توصیف آن‌ها پرداختیم، قادر هستند که اکثر انواع کانال‌های فیزیکی را به صورت مناسب توصیف کنند و به همین دلیل برای طراحی و آنالیز سیستم‌های مخابراتی به صورت گسترده مورد استفاده قرار می‌گیرند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مبانی سیستم های مخابراتی‎
• مجموعه آموزش‌های مهندسی برق
• آموزش مدارهای مخابراتی
• حلقه قفل فاز (PLL) چیست؟ — از صفر تا صد
• اتوماتای سلولی چیست؟ — راهنمای جامع
• مدولاسیون فاز — راهنمای جامع

^^