مدولاتور AM — از صفر تا صد

در مطالب قبلی به بیان هدف از مدولاسیون پرداختیم و نیز مباحث تئوری روش مدولاسیون دامنه (Amplitude Modulation) یا AM را بیان کردیم. در این مطلب قصد داریم تا به معرفی انواع مداراتی بپردازیم که با هدف انجام مدولاسیون دامنه یا مدولاسیون AM مورد استفاده قرار می‌گیرند. به این مدارات، مدولاتور AM می‌گویند.

در حالت کلی می‌توان گفت دو مدار اصلی به عنوان مدولاتور AM وجود دارند. این مدارات عبارتند از:

1. مدولاتور AM مجذوری یا قانون مربع (Square law Modulator)
2. مدولاتور AM ﺳﻮﺋﯿﭽﯿﻨﮓ (Switching Modulator)

مدولاتور AM مجذوری یا قانون مربع

در تصویر زیر نمایش بلوک دیاگرام یک مدولاتور مجذوری یا قانون مربع نشان داده شده است.

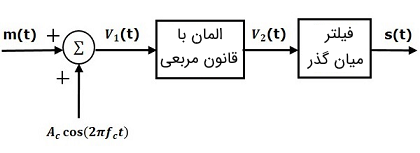
حال فرض کنید سیگنال مدوله کننده یا سیگنال پیام را با $$ m \left ( t \right )  $$ و سیگنال حامل را با $$ A \cos \left ( 2 \pi f _ c t \right ) $$ نمایش دهیم. این دو سیگنال به عنوان ورودی به بلوک جمع‌ کننده (Summer Block) وارد می‌شوند. بلوک جمع کننده یک خروجی را تولید می‌کند که برابر با مجموع سیگنال پیام و سیگنال حامل است.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

این خروجی را می‌توان به صورت ریاضی بر اساس معادله زیر بیان کرد:

$$ V _ 1 t = m \left ( t \right ) + A _ c \cos \left ( 2 \pi f _ c t \right ) $$

این سیگنال، یعنی $$ V _ 1 t $$ به عنوان ورودی به یک المان غیر خطی مانند دیود اعمال می‌شود. منحنی مشخصه دیود، تا حد بسیار زیادی به یک معادله درجه دو (Square Law) شبیه است. این معادله در زیر آورده شده است:

$$ V _ 2 t = k _ 1 V _ 1 \left ( t \right ) + k _ 2 V _ 1 ^ 2 \left ( t \right ) \; \; \; \; \; \; \; \; \; (1) $$

در معادله بالا، $$ k _ 1 $$ و $$ k _ 2 $$ ضرایبی ثابت محسوب می‌شوند. حال با جایگذاری مقدار $$ V _ 1 \left (t \right ) $$ در معادله شماره ۱، به رابطه زیر دست می‌یابیم:

$$ V _ 2 \left (t\right ) = k _ 1 \left [ m \left ( t \right ) + A _ c \cos \left ( 2 \pi f _ c t \right ) \right ] + k _ 2 \left [ m \left ( t \right ) + A _ c \cos\left ( 2 \pi f _ c t \right ) \right ] ^ 2 $$

$$ \Rightarrow V _ 2 \left ( t \right ) = k _ 1 m \left ( t \right ) + k _ 1 A _ c \cos \left ( 2 \pi f _ c t \right ) + k _ 2 m ^ 2 \left ( t \right ) + \\ k _ 2 A _ c ^ 2 \cos ^ 2 \left ( 2 \pi f _ c t \right ) + 2 k _ 2 m \left ( t \right )A _ c \cos \left ( 2 \pi f _ c t \right ) $$

$$ \Rightarrow V _ 2 \left ( t \right ) = k _ 1 m \left ( t \right ) + k _ 2 m ^ 2 \left ( t \right ) + k _ 2 A ^ 2 _ c \cos ^ 2 \left ( 2 \pi f_ c t \right ) + \\ k _ 1 A _ c \left [ 1 + \left ( \frac { 2 k _ 2 } { k _ 1 } \right ) m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

آخرین عبارت از رابطه فوق، یک موج AM محسوب می‌شود. در واقع هدف یک مدار مدولاتور AM تولید این سیگنال است. به همین دلیل به راحتی می‌توان گفت که سه عبارت دیگر در رابطه به دست آمده، بدون استفاده هستند و باید آن‌ها را حذف کرد. بنابراین با استفاده از یک فیلتر میان گذر (Band Pass Filter)، می‌توانیم فقط قسمت سیگنال AM عبارت فوق را گذر دهیم و سه عبارت دیگر را فیلتر کنیم. در نهایت می‌توان گفت که خروجی یک مدولاتور مجذور یا قانون مربع به صورت زیر به دست می‌آید:

$$ s \left ( t \right ) = k _ 1 A _ c \left [ 1 + \left ( \frac { 2 k _ 2 } { k _ 1 } \right ) m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

از قبل می‌دانیم که معادله استاندار یک سیگنال AM به صورت زیر نوشته می‌شود:

$$ s \left ( t \right ) = A _ c \left [ 1 + k _ a m \left ( t \right ) \right ] \cos \left (2 \pi f _ c t \right ) $$

در معادله فوق، $$ K _ a $$ به عنوان حساسیت دامنه در نظر گرفته می‌شود.

حال با مقایسه کردن سیگنال خروجی مدار مدولاتور قانون مربع و سیگنال AM حاصل از معادله استاندارد، فاکتور مقیاس را برابر با $$ k _ 1 $$ و نیز حساسیت دامنه $$ K _ a $$ را برابر با $$ \frac { 2 k _ 2 } { k _ 1 } $$ را به دست می‌آوریم.

مدولاتور AM ﺳﻮﺋﯿﭽﯿﻨﮓ

در تصویر زیر بلوک دیاگرام یک مدار مدولاتور ﺳﻮﺋﯿﭽﯿﻨﮓ نشان داده شده است.

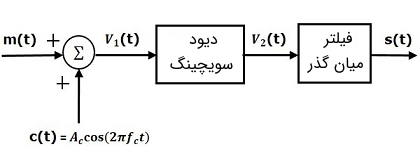
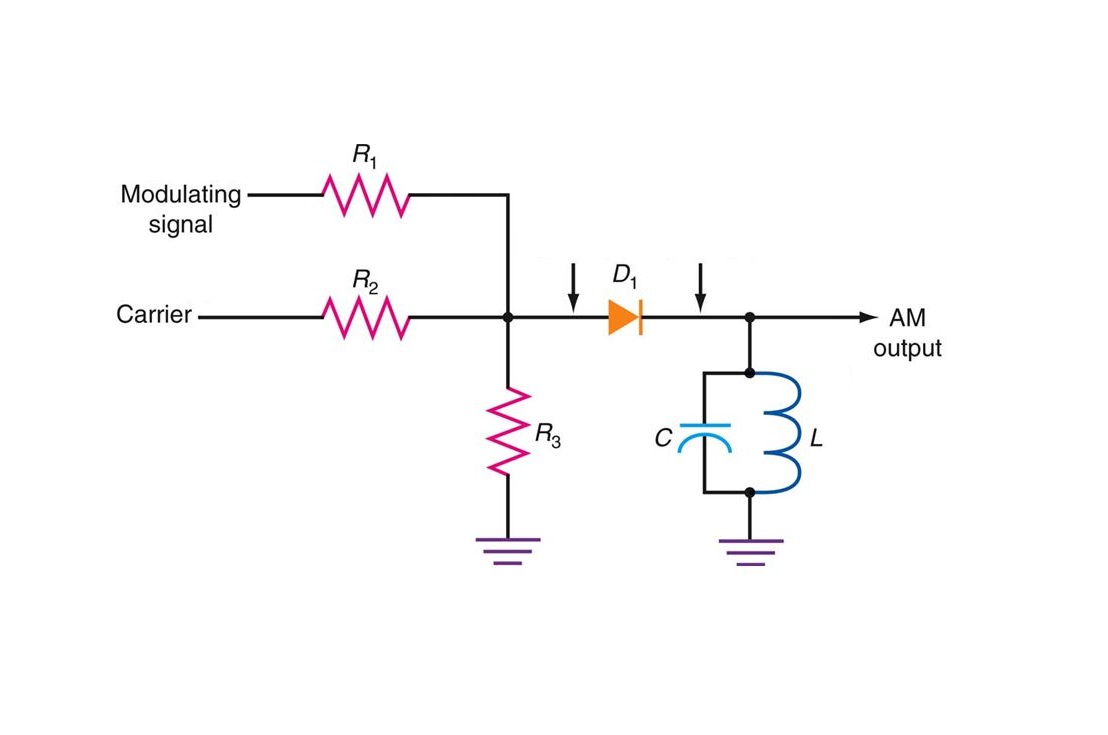
عملکرد مدار مدولاتور ﺳﻮﺋﯿﭽﯿﻨﮓ بسیار شبیه به مدار مدولاتور قانون مربع است. تنها تفاوت این دو مدار در این است که در مدولاتور قانون مربع، دیود در مود غیر خطی عمل می‌کند، در حالی که در مدار مدولاتور ﺳﻮﺋﯿﭽﯿﻨﮓ، دیود باید به عنوان یک کلید ایده‌آل عمل کند.

فیلم آموزش مدارهای مخابراتی در فرادرس

کلیک کنید

حال می‌خواهیم سیگنال پیام را با $$ m \left ( t \right ) $$ و سیگنال حامل را با $$ c \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) $$ نشان دهیم. این دو سیگنال به عنوان ورودی به بلوک جمع کننده وارد می‌شوند. بنابراین بلوک جمع کننده خروجی را تولید می‌کند که برابر با مجموع سیگنال پیام و نیز سیگنال حامل است. این سیگنال را می‌توان به صورت ریاضی با رابطه زیر نشان داد:

$$ V _ 1 \left ( t \right ) = m \left ( t \right ) + c \left ( t \right ) = m \left ( t \right ) + A _ c \cos \left ( 2 \pi f _ c t \right ) $$

سیگنال $$ V _ 1 \left ( t \right ) $$ به عنوان ورودی به یک دیود وارد می‌شود. فرض کنید دامنه سیگنال پیام در مقایسه با سیگنال حامل $$ A _ c $$ بسیار کوچک باشد. بنابراین وضعیت خاموش و روشن دیود توسط سیگنال حامل $$ c \left ( t \right ) $$ کنترل می‌شود. این امر بدین معنی است که در شرایطی که $$ c \left ( t \right ) > 0 $$ باشد، دیود در مود بایاس مستقیم قرار می‌گیرد و زمانی که $$ c \left ( t \right ) < 0 $$ باشد، دیود در مود بایاس معکوس قرار خواهد گرفت. بنابراین خروجی دیود به صورت زیر به دست می‌آید:

$$ V _ 2 \left ( t \right ) = \left \{ \begin {matrix}
V _ 1 \left ( t \right ) & if & c \left ( t \right ) > 0 \\
0& if & c\left ( t \right )<0
\end {matrix}\right. $$

این سیگنال را می‌توان به صورت زیر تقریب زد:

$$ V _ 2 \left ( t \right ) = V _ 1 \left ( t \right ) x \left ( t \right )\; \; \; \; \; \; \; \; \; (2) $$

در معادله فوق، $$ x \left ( t \right ) $$ یک قطار پالس متناوب با دوره تناوب $$ T = \frac { 1 } { f _ c } $$ است. نمایی از قطار پالس متناوب $$ x \left ( t \right ) $$ در تصویر زیر نشان داده شده است.

نمایش سری فوریه قطار پالس متناوب را می‌توان به صورت زیر نوشت:

$$ x \left ( t \right ) = \frac { 1 } { 2 } + \frac { 2 } { \pi }\sum _ { n = 1 } ^ { \infty } \frac { \left ( -1 \right ) ^ n - 1 } { 2 n - 1 } \cos \left (2 \pi \left ( 2 n - 1 \right ) f _ c t \right ) $$

$$ \Rightarrow x \left ( t \right ) = \frac { 1 } { 2 } + \frac { 2 } { \pi } \cos \left ( 2 \pi f _ c t \right ) - \frac { 2 } { 3 \pi } \cos \left ( 6 \pi f_ c t \right ) + . . . . $$

حال با جایگذاری مقادیر $$ V _ 1 \left ( t \right ) $$ و $$ x \left ( t \right ) $$ در معادله شماره ۲، به نتیجه زیر می‌رسیم:

$$ V _ 2 \left ( t \right ) = \left [ m \left ( t \right ) + A _ c \cos \left ( 2 \pi f _ c t \right ) \right ] \left [ \frac { 1 } { 2 } + \frac { 2 } { \pi } \cos \left ( 2 \pi f _ c t \right ) - \frac { 2 } { 3 \pi } \cos \left ( 6 \pi f _ c t \right ) + . . . . . \right ] $$

$$ V _ 2 \left ( t \right ) = \frac { m \left ( t \right ) } { 2 } + \frac { A _ c} { 2 } \cos \left ( 2 \pi f _ c t \right ) + \frac { 2 m \left ( t \right ) } { \pi } \cos \left ( 2 \pi f _ c t \right ) +\frac { 2 A _ c } { \pi } \cos ^ 2 \left ( 2 \pi f _ c t \right ) - \\
\frac { 2 m \left ( t \right ) } { 3 \pi} \cos \left ( 6 \pi f _ c t \right ) - \frac { 2 A _ c } { 3 \pi } \cos \left ( 2 \pi f _ c t \right ) \cos \left ( 6 \pi f _ c t \right ) + . . . . . $$

$$ V _ 2 \left ( t \right ) = \frac { A _ c } { 2 } \left ( 1 + \left ( \frac { 4 } { \pi A _ c } \right ) m \left ( t \right ) \right ) \cos \left ( 2 \pi f _ c t \right ) + \frac { m \left ( t \right ) } { 2 } + \frac { 2 A _ c } { \pi } \cos ^ 2 \left ( 2 \pi f _ c t \right ) - \\
\frac { 2 m \left ( t \right ) } { 3 \pi } \cos \left ( 6 \pi f _ c t \right ) - \frac { 2 A _ c } { 3 \pi } \cos \left ( 2 \pi f _ c t \right ) \cos \left ( 6 \pi f _ c t \right ) + . .. . . $$

اولین عبارت در رابطه بالا، نمایش دهنده سیگنال AM مطلوب ما است و بقیه عبارات نامطلوب هستند و باید حذف شوند. بنابراین از یک فیلتر میان گذر استفاده می‌کنیم و فقط سیگنال AM مطلوب را به خروجی مدار مدولاتور AM عبور می‌دهیم و اجازه گذر مابقی عبارات را نمی‌دهیم و آن‌ها را توسط فیلتر حذف می‌کنیم.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

در نهایت معادله سیگنال خروجی از مدولاتور ﺳﻮﺋﯿﭽﯿﻨﮓ به صورت زیر به دست می‌آید:

$$ s \left ( t \right ) = \frac { A _ c } { 2 } \left ( 1 + \left ( \frac { 4 } { \pi A _ c } \right ) m \left ( t \right ) \right ) \cos \left ( 2 \pi f _ c t \right ) $$

از قبل می‌دانیم که معادله استاندارد سیگنال مدولاسیون AM به صورت زیر نوشته می‌شود:

$$ s \left ( t \right ) = A _ c \left [ 1 + k _ a m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

در این رابطه $$ k _ a $$ برابر با حساسیت دامنه است. حال از طریق مقایسه کردن خروجی حاصل از یک مدار مدولاتور AM ﺳﻮﺋﯿﭽﯿﻨﮓ با سیگنال استاندار مدولاسیون AM، به یک فاکتور مقیاس به اندازه ۰٫۵ و حساسیت دامنه $$ k _ a $$ به اندازه $$ \frac { 4 } { \pi A _ c } $$ دست می‌یابیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌ مهندسی الکترونیک
• آموزش مبانی ​الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
• مدولاسیون فرکانس — از صفر تا صد
• انرژی و توان سیگنال — از صفر تا صد
• مدولاسیون فاز — راهنمای جامع

^^