فرادرس
ماتریس اسکالر چیست؟ | تعریف و محاسبات روی ماتریس اسکالر — به زبان ساده
به طور حتم با ماتریس و مفهوم آن در ریاضیات آشنا هستید. یک روش برای بیان مجموعه‌ای از اعداد مرتبط، قرار دادن آن‌ها در یک ساختار منظم به نام ماتریس است. در ماتریس‌ها، اعضا یا درایه‌ها در محل تفاطع سطر و ستون‌ها نوشته می‌شوند. ابعاد ماتریس، نوع قرارگیری درایه‌ها و ویژگی‌های ماتریس، باعث معرفی و نامگذاری انواع ماتریس‌ها مانند ماتریس مربعی، ماتریس یکه و غیره شده است. در این متن می‌خواهیم با نوع خاصی از ماتریس به نام ماتریس اسکالر آشنا شویم و ویژگی‌های آن را به شما معرفی کنیم.
به عنوان مقدمه و پیش‌نیاز این متن بهتر است نوشتارهای دیگر مجله فرادرس مانند ماتریس چیست ؟ | ماتریس در ریاضی — به زبان ساده و خواص ماتریس ها — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب ماتریس مربعی و خصوصیات آن — از صفر تا صد و ماتریس همانی و ماتریس یکانی | به زبان ساده نیز خالی از لطف نیست.
ماتریس اسکالر
ماتریس‌ها در جبر خطی و حل دستگاه معادلات به کار گرفته می‌شوند. بسیاری از مسائل چند متغیره در ریاضی به کمک ماتریس‌ها حل می‌شوند. به همین جهت در اکثر مواقع در ریاضیات با ماتریس‌ها سروکار خواهیم داشت.
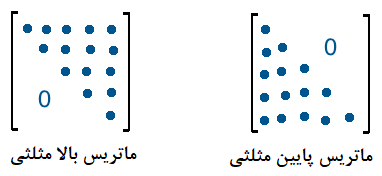
با توجه به ویژگی‌هایی که ماتریس‌ها دارند، آن‌ها را به دسته‌های مختلفی طبقه‌بندی کرده‌اند. ماتریس قطری، ماتریس بالا مثلثی و ماتریس مربعی، بعضی از این گروه‌بندی‌ها را نشان می‌دهند. در تصویر بالا، نمایی از ماتریس های پایین مثلثی و بالا مثلثی را مشاهده می‌کنید. در ماتریس پایین مثلثی، درایه‌های پایین قطر اصلی، همگی صفر هستند. در ماتریس بالا مثلثی نیز تمامی درایه های بالای قطر اصلی صفر خواهند بود.
در ریاضیات، گاهی بردارها را به هم به صورت ماتریسهای ستونی یا سطری نمایش داده و عملگرهای ماتریسی مانند جمع و تفریق یا ضرب را روی آن‌ها به شیوه ماتریسی اجرا می‌کنند.
در تصویر زیر یک ماتریس مربعی دو در دو را مشاهده می‌کنید که درایه‌های آن با مقادیر ۳، ۸، ۴ و ۶ مشخص شده‌اند.
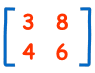
واضح است که ستون اول مقادیر ۳ و ۴ را دارد و ستون دوم نیز از مقادیر ۸ و ۶ تشکیل شده. از آنجایی که تعداد سطرها و ستون‌های این ماتریس یکسان است، آن را ماتریس مربعی می‌نامیم. ولی برای ماتریس اسکالر احتیاج به یک ماتریس قطری داریم.
ماتریسی که مربعی بوده و همگی عناصر غیر قطر آن صفر باشند، یک ماتریس قطری نامیده می‌شود. برای مثال اگر بخواهیم یک ماتریس قطری ۳ در ۳ را نشان دهیم، از نمایشی به شکل زیر استفاده خواهیم کرد.
$$ \large {\displaystyle \begin{bmatrix} a & 0 &0 \\ 0 & b & 0 \\ 0 & 0 & c \end{bmatrix}}$$
همانطور که می‌بینید، عناصر روی قطر اصلی به ترتیب a و b و c هستند ولی عناصر خارج قطر، همگی صفر خواهند بود در غیر اینصورت ماتریس را قطری نمی‌شناسیم.
در این متن می‌خواهیم به ماتریس اسکالر بپردازیم که در فضای ماتریسی به عنوان یک مقدار ثابت برای عملگر ضرب خواهد بود. یک ماتریس اسکالر درست به مانند عدد ثابت در محاسبات حساب در نظر گرفته می‌شود. در ادامه به تعریف ماتریس اسکالر خواهیم پرداخت.
با توجه به گسترش جبر خطی در مباحث ریاضی و کاربرد آن در رشته‌های مهندسی، فنی و ریاضی، فرادرس به تازگی دست به انتشار فیلم آموزش مرتبط با این موضوع زده است. در ادامه لینک دسترسی به این فیلم آموزش جبر خطی قرار داده شده که با مشاهده آن قادر به درک و آشنایی کامل با مباحث جبر خطی خواهید شد.
- برای مشاهده فیلم آموزش جبر خطی + اینجا کلیک کنید.
تعریف ماتریس اسکالر
ماتریس قطری و مربعی با درایه‌هایی که روی قطر اصلی آن، یکسان و برابر باشند، یک ماتریس اسکالر نامیده می‌شود. به این معنی که اگر یک ماتریس قطری، عناصر قطر اصلی آن همگی برابر با $$\lambda$$ باشد، یک ماتریس اسکالر خواهد بود. در زیر یک نمونه از ماتریس اسکالر سه در سه را مشاهده می‌کنید.
$$ \large {\displaystyle \begin{bmatrix} \lambda & 0 &0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix}}$$
واضح است که می‌توان با فاکتورگیری از مقدار $$\lambda$$ و ضرب اسکالر در ماتریس یکه، به تساوی زیر رسید.
$$ \large {\displaystyle \begin{bmatrix} \lambda & 0 &0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix} =} $$
$$ \large {\displaystyle \lambda \begin{bmatrix} \lambda & 0 &0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix} = \lambda I_{3 \times 3 } }$$
که در آن منظور از $$I_{3 \times 3}$$ ماتریس یکه سه در سه است. اگر برای مثال مقدار $$\lambda$$ را برابر با ۵ در نظر بگیریم، ماتریس اسکالر تعریف شده در بالا، به صورت زیر در خواهد آمد.
$$ \large {\displaystyle \begin{bmatrix} 5 & 0 &0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{bmatrix}}$$
ماتریسهای اسکالر، مرکز جبر ماتریس‌ها هستند، یعنی دقیقاً ماتریس‌هایی هستند که با تمام ماتریسهای مربع دیگر در رابطه بوده و می‌توانند به عنوان ضریب در ماتریس ها به کار روند. چنین ماتریسی‌هایی، درست نقش اعداد حقیقی و ثابت را در جبر خطی بخصوص ضرب ماتریس‌ها ایفا می‌کنند.
جمع و تفریق با ماتریس اسکالر
جمع و تفریق ماتریسی با ماتریس اسکالر، باعث افزایش یا کاهش عناصر قطر اصلی ماتریس‌ها به میزان ثابت خواهد شد. برای مثال به رابطه‌های زیر توجه کنید.
$$ \large {\displaystyle \begin{bmatrix} 10 & 1 & 8 \\ 3 & 1 & 4 \\ 7 & 6 & 15 \end{bmatrix} + \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} =} $$
$$ \large {\displaystyle \begin{bmatrix} 11 & 1 & 8 \\ 3 & 2 & 4 \\ 7 & 6 & 16 \end{bmatrix} }$$
یا برای تفریق به صورت زیر درخواهد آمد.
$$ \large {\displaystyle \begin{bmatrix} 10 & 1 & 8 \\ 3 & 1 & 4 \\ 7 & 6 & 15 \end{bmatrix} -\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = }$$
$$ \large {\displaystyle \begin{bmatrix} 9 & 1 & 8 \\ 3 & 0 & 4 \\ 7 & 6 & 14 \end{bmatrix} }$$
توجه دارید که در اینجا هر دو ماتریس باید دارای ابعاد یکسان باشند تا جمع و تفریق، قابل اجرا باشد در غیر اینصورت امکان جمع یا تفریق آن‌ها وجود ندارد.
ضرب ماتریس اسکالر در ماتریس دیگر
این بار به سراغ ضرب دو ماتریس می‌رویم که یکی از آن‌ها ماتریس اسکالر است. مثلا فرض کنید که حاصل ضرب ماتریسهای زیر را احتیاج داریم. واضح است که ماتریس اول یک ماتریس مربعی بوده و ماتریس دوم، یک ماتریس اسکالر است.
$$ \large {\displaystyle \begin{bmatrix} 10 & 1 & 8 \\ 3 & 1 & 4 \\ 7 & 6 & 15 \end{bmatrix} \times \begin{bmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix} }$$
در نتیجه رابطه نهایی به شکل زیر خواهد بود.
$$ \large {\displaystyle \begin{bmatrix} 30 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 45 \end{bmatrix} } $$
که یک ماتریس قطری با درایه‌هایی برابر با ۳ برابر ماتریس اولیه است. البته اگر با فاکتورگیری از مقدار ثابت از ماتریس اسکالر ضرب را انجام دهیم به همان نتیجه خواهیم رسید.
$$ \large {\displaystyle 3 \begin{bmatrix} 10 & 1 & 8 \\ 3 & 1 & 4 \\ 7 & 6 & 15 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} =}$$
$$ \large {\displaystyle \begin{bmatrix} 30 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 45 \end{bmatrix} }$$
به این ترتیب رابطه ماتریس اسکالر و عدد ثابت در ضرب ماتریس‌ها به خوبی نمایش داده شد.
نکته: توجه داشته باشید که ضرب یک عدد در ماتریس، به معنی ضرب همه درایه‌ها آن در عدد ثابت است. ولی معنی ضرب ماتریس در ماتریس اسکالر معنی متفاوتی دارد و هر ماتریسی را به یک ماتریس قطری تبدیل می‌کند. بنابراین در چنین حالتی، اگر ماتریس اول را در ۳ ضرب کرده، سپس در ماتریس همانی ضرب ماتریسی کنیم، نتیجه یکسانی با ضرب ماتریس اولیه در ماتریس اسکالر خواهیم گرفت. در حالیکه، ضرب ماتریس اولی در عدد ۳ (بدون در نظر گرفتن ماتریس همانی) نتیجه‌ای دیگر به همراه خواهد داشت.
ماتریس قطری و ماتریس اسکالر در برنامه R
برای ایجاد ماتریس قطری در برنامه R از دستور diag استفاده می‌شود. برای مثال دستور زیر باعث ایجاد یک ماتریس قطری یا‌به شکلی، ر حقیقت ماتریس اسکالر سه در سه خواهد شد که درایه‌های قطر اصلی آن ۱ هستند. پارامتر ۳ در اینجا به معنی ابعاد ماتریس مربعی یا قطری است.
> diag(3)
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
>
ولی اگر بخواهید ماتریس اسکالری ایجاد کنید که درایه‌های قطر اصلی آن مثلا ۵ باشد ولی یک ماتریس مربع ۳ در ۳ تشکیل شود، دستور diag را به صورت زیر اجرا خواهیم کرد.
> diag(5, 3 , 3)
[,1] [,2] [,3]
[1,] 5 0 0
[2,] 0 5 0
[3,] 0 0 5
>
در قطعه کد بالا، مشخص است که ۵ مقدار درایه‌ها قطر اصلی بوده و ۳ و ۳ ابعاد ماتریس قطری را مشخص کرده‌اند. البته در اینجا می‌توان تعداد ستون‌ها با تعداد سطرها را یکسان وارد نکرده و ماتریس حاصل، مربعی نباشد. دستور زیر یک ماتریس ۳ در ۴ ایجاد کرده و عناصر روی قطر اصلی آن همگی ۵ هستند.
> diag(5, 3 , 4)
[,1] [,2] [,3] [,4]
[1,] 5 0 0 0
[2,] 0 5 0 0
[3,] 0 0 5 0
>
همچنین در دستور diag می‌توان با معرفی یک بردار برای عناصر قطر اصلی، ماتریس قطری را از حالت اسکالر خارج کرد. به قطعه کد و نتیجه ظاهر شده که در ادامه دیده می‌شود، توجه کنید.
diag(c(10,20,30), 3 , 4)
[,1] [,2] [,3] [,4]
[1,] 10 0 0 0
[2,] 0 20 0 0
[3,] 0 0 30 0
همانطور که می‌بینید، عناصر روی قطر اصلی، مقدارهای ۱۰، ۲۰ و ۳۰ هستند ولی ماتریس حاصل، مربعی نیز نیست.
معرفی فیلم آموزش جبر خطی
جبر خطی، از مهم‌ترین شاخه‌های ریاضیات مدرن محسوب شده و پرکاربردترین بخش ریاضی در رشته‌های فنی و بخصوص در زمینه‌های چند متغیره است. در مدل سازی علوم مهندسی، توصیف پدیده‌های طبیعی چند متغیره، جبر خطی مورد استفاده قرار می‌گیرد. هدف از این آموزش، آشنایی فراگیران با مفاهیم و مبانی جبر خطی و کاربردهای آن است. در این بین تکنیک‌های حل دستگاه معادلات خطی، جبر بردارها مورد توجه قرا گرفته و به آنالیز ماتریسی، تبدیلات ماتریسی و خطی به همراه دترمینان، مقادیر ویژه و بردارهای ویژه نیز پرداخته شده است. فهرست سرفصل‌ها و رئوس مطالب مطرح شده در این مجموعه آموزشی، در ادامه آمده است.
زمان محتویات ویدیویی این آموزش ۱۷ ساعت و ۳۲ دقیقه است که بخصوص برای دانشجویان فنی و مهندسی و همچنین ریاضی کاربردی و آمار بسیار مناسب است.
- برای مشاهده فیلم آموزش جبر خطی + اینجا کلیک کنید.
خلاصه و جمع‌بندی
در این متن از نوشتارهای مجله فرادرس، با مفهوم ماتریس اسکالر آشنا شدید و کاربردهای آن را در عملیات ماتریسی، بخصوص ضرب ماتریس‌ها مشاهده کردید. از ماتریس اسکالر برای نمایش ضرب یک مقدار ثابت در ماتریس استفاده می‌شود، بطوری که همه طرف‌های ضرب ماتریس باشند.
به این ترتیب ضرب یک عدد مشخص در ماتریس را به صورت ضرب دو ماتریس در آورده و نتیجه را به دست می‌آوریم. البته عمل عکس نیز امکان‌پذیر است به این معنی که ضرب دو ماتریس که یکی از آن‌ها ماتریس قطری با مقادیر ثابت است را می‌توان به صورت ضرب یک ماتریس در مقدار ثابت در نظر گرفت، به طوری که همه درایه‌های آن را در مقدار ثابت ضرب کنیم.
در فضای برداری و همچنین جبر ماتریس‌ها، ماتریس اسکالر نقش مهم و پایه‌ای در ریاضیات دارد. درست به همان صورت که عدد یک، در هنگام ضرب اعداد حقیقی، نقش مقدار عضو خنثی را ایفا می‌کند، ماتریسهای اسکالر نیز می‌توانند چنین نقشی در فضای برداری و عمل ضرب ماتریس‌ها داشته باشند و به کمک آن‌ها، ماتریس‌ها را به ماتریس‌ها قطری تبدیل کرده و استفاده نمود.
