ماتریس همانی و ماتریس یکانی | به زبان ساده

در پدیده‌های طبیعی، اغلب با بیش از یک ویژگی مواجه هستیم. برای بیان ویژگی‌های این پدیده‌ها، از ساختاری به نام «ماتریس» (Matrix) استفاده می‌کنیم. در این بین ماتریس‌های مختلف با خواص متفاوت به کار می‌روند. در این نوشتار از مجله فرادرس با دو گونه ماتریس خاص آشنا خواهیم شد که به ماتریس همانی و ماتریس یکانی معروف هستند.

ماتریس همانی یا ماتریس یکه (Identity Matrix) نقش مقدار ۱ را در عمل ضرب حسابی ایفا می‌کند و به عنوان یک عنصر بی‌اثر در عملگر ضرب ماتریسی به کار می‌رود. همچنین ماتریس یکانی (Unitary Matrix) نیز شبیه «عدد موهوی» (Imaginary Unit) با مقدار $$i^2 = -1$$ در محاسبات «اعداد مختلط» (Complex Numbers) است. به این ترتیب مشخص است که هر دو ماتریس ماتریس همانی و ماتریس یکانی نقش مهمی در جبر ماتریس‌ها به عهده دارند.

به منظور آشنایی بیشتر با مفاهیم به کار رفته در این متن بهتر است ابتدا مطالب ماتریس‌ها در ریاضی — به زبان ساده و خواص ماتریس ها — به زبان ساده از مجله فرادرس را بخوانید. همچنین خواندن نوشتارهای ماتریس هرمیتی و خصوصیات آن — به زبان ساده و ضرب ماتریس‌ها — به زبان ساده نیز خالی از لطف نیست.

ماتریس همانی و ماتریس یکانی

جبر ماتریسی یا «جبر خطی» (Linear Algebra)، توسعه‌ای بر جبر و حساب اعداد محسوب می‌شود. به این ترتیب همان عملیاتی که برای اعداد (نظیر چهار عمل اصلی) وجود دارد، برای ماتریس‌ها نیز تعریف و به کار گرفته می‌شود.

یکی از این عملگرها که در حساب ماتریس‌ها و جبر خطی از اهمیت زیادی برخوردار است، «ضرب ماتریسی» (Matrix Multiplication) است. در «نظریه مجموعه‌ها» (Set Theory)، سعی می‌شود همه شاخه‌های ریاضی طبق اصولی که در این نظریه ایجاد شده است، تبیین شوند. جبر خطی نیز از این موضوع مستثنی نیست. بنابراین طبق مفاهیم مربوط به میدان (Field)، گروه (Group) و حلقه (Ring)، باید بتوان عنصر بی‌اثر در عملگر به کار رفته در جبر ماتریس‌ها را مشخص کرد. این جاست که پای دو ماتریس همانی و ماتریس یکانی به میان می‌آید.

ماتریس همانی و ماتریس یکانی نقش مهمی در تفسیر مفاهیم نظریه مجموعه‌ها در جبر خطی ایفا می‌کنند. به همین دلیل در این متن به معرفی این دو ماتریس خواهیم پرداخت. البته به خصوصیاتی که در جبر خطی چه در فضای اعداد حقیقی یا اعداد مختلط برای ماتریس همانی و ماتریس یکانی وجود دارد نیز اشاره‌هایی خواهیم داشت.

ماتریس همانی

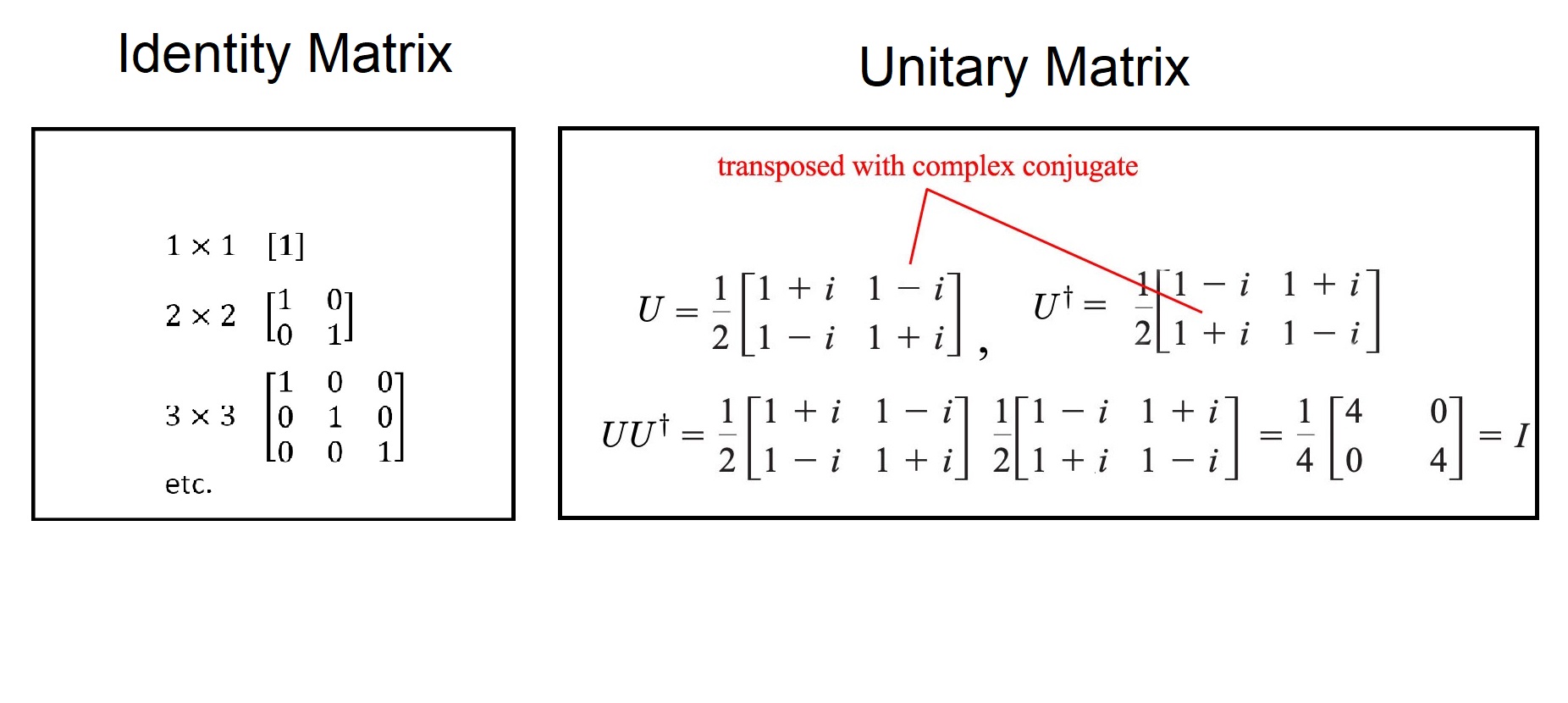
در جبر خطی، «ماتریس همانی» (Identity Matrix) یا «ماتریس یکه» (Unit Matrix)، یک «ماتریس مربعی» (Square Matrix) است که درایه‌های روی قطر اصلی آن برابر با ۱ بوده و عناصر خارج از قطر، همگی صفر هستند.

ماتریس همانی را اغلب با نماد $$I_{n}$$ نشان می‌دهند که اندیس $$n$$، بیانگر بعد ماتریس همانی است. البته گاهی این ماتریس به شکل عدد یک ضخیم (1) مشخص می‌شود. همچنین نمادهای $$U$$ و $$E$$ نیز برای این ماتریس به ندرت به کار می‌روند.

به عنوان مثال، ماتریس‌های زیر همگی از نوع همانی هستند.

$$ \large {\displaystyle I_{1} = {\begin{bmatrix}1 \end{bmatrix}},\ I_{2} ={\begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}},\ I_{3}= {\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}},\ \cdots ,\ I_{n} = {\begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{bmatrix}}} $$

اگر از نماد ماتریس قطری (Diagonal Matrices) استفاده کنیم، ماتریس همانی به شکل زیر نوشته خواهد شد.

$$ \large {\displaystyle I_{n} = \operatorname {diag} (1 , 1 , \dots ,1 ) } $$

همچنین به کمک «تابع دلتای کرونکر» (Kronecher Delta Function) نیز، ماتریس همانی به شکل زیر بیان می‌شود.

$$ \large {\displaystyle (I_{n})_{ij} = \delta_{ij}} $$

خواص ماتریس همانی

فرض کنید که $$A$$ یک ماتریس با ابعاد $$m \times n $$ باشد. در این صورت اگر $$I_n$$‌، ماتریس همانی با $$n$$ سطر و $$I_m$$ نیز ماتریسی با $$m$$ ستون باشد، رابطه زیر براساس ضرب ماتریسی برقرار است.

$$ \large {\displaystyle I_{m} A = AI_{n}= A } $$

رابطه ۱: تعریف ماتریس همانی

به این ترتیب می‌توان ماتریس همانی را به عنوان عنصر همانی در حلقه (Ring) حاصل از فضای ماتریسی و عملگر ضرب ماتریسی در نظر گرفت. با توجه به رابطه ۱ می‌توان نتیجه گرفت که ماتریس همانی، معکوس خودش است. با فرض $$A_{n \times n } = I_n$$، نتیجه می‌گیریم:

$$ \large {\displaystyle I_{n} I_{n} =  I_{n} } $$

رابطه ۲: خودتوانی ماتریس همانی

که نشانگر معکوس‌پذیری ماتریس همانی است. به این ترتیب رابطه ۲ نشان می‌دهد که ماتریس همانی با توجه به عمل ضرب، یک «ماتریس خودتوان» (Idempotent Matrix) هم خواهد بود.

نکته: در حقیقت ماتریس همانی تنها ماتریس خودتوانی است که دترمینان آن صفر نیست. مشخص است که دترمینان ماتریس همانی برابر با یک است.

زمانی که از ماتریس‌های مربعی با $$n$$‌ سطر یا ستون برای بیان تبدیلات خطی در فضای $$n$$ بُعدی به همان فضا استفاده می‌شود، ماتریس $$I_n$$ ‌نقش «تابع همانی» (Identity Function) را ایفا می‌کند. واضح است که در این حالت نیازی به مشخص کردن پایه‌ها نیست.

هر ستون (یا هر سطر) از ماتریس همانی، یک بردار با طول واحد است که به آن «بردار یکه» (Unit Vector) گفته می‌شود. به این ترتیب اگر $$i$$امین ستون ماتریس همانی را در نظر بگیریم، یک بردار به صورت $$e_i$$ و به شکل زیر خواهد بود.

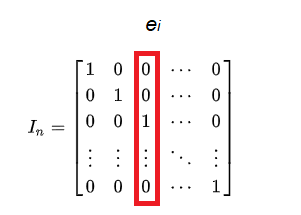
با توجه به ساختاری که ماتریس همانی دارد، واضح است که سطرها و ستون‌های آن «مستقل خطی» (Linear Independent) از یکدیگر هستند.

همچنین «ریشه دوم اصلی» (Principle Square Root) یا جذر اصلی ماتریس همانی، خود ماتریس همانی است و تنها ماتریس است که ریشه دوم آن «مثبت معین» (Positive Definite) است.

نکته: هر ماتریس همانی با حداقل دو سطر یا ستون، دارای بی‌شمار ریشه دوم قرینه است. برای مثال، ریشه‌های دوم ماتریس همانی $$I_2$$ به صورت‌های زیر می‌توانند نوشته شوند.

$$\large {\displaystyle {\dfrac {1}{t}} {\bigl (} {\begin{matrix} \mp s & \mp r \\ \large \mp r & \pm s \end{matrix}} { \bigr) }} $$

$$ \large {\displaystyle {\dfrac {1}{t}} {\bigl (} {\begin{matrix} \pm s & \mp r \\ \large \mp r & \mp s \end{matrix}} { \bigr) }} $$

$$ \large {\displaystyle {\dfrac {1}{t}} {\bigl (} {\begin{matrix} \mp r & \mp s \\ \large \mp s & \pm r \end{matrix}} { \bigr) }} $$

$$ \large {\displaystyle {\dfrac {1}{t}} { \bigl ( } {\begin{matrix}\pm r&\mp s\\ \large \mp s & \mp r \end{matrix}}{ \bigr) }}$$

که در آن‌ها رابطه زیر بین اعداد صحیح $$t$$، $$r$$ و $$s$$ برقرار است. چنین اعدادی را اعداد «سه گانه فیثاغورسی» (Pythagorean triple) می‌نامیم.

$$ \large t^2 = s^2 + r^2 $$

همچنین دو ماتریس زیر نیز به عنوان ریشه‌های دوم ماتریس همانی محسوب می‌شوند.

$$ \large {\displaystyle {\bigl(} { \begin{matrix}1 & 0 \\ 0 & \pm 1 \end{matrix}}{\bigr)} } $$

$$ \large {\displaystyle {\bigl(}{ \begin{matrix} \pm 1 & 0 \\ 0 & 1 \end{matrix}}{\bigr )}}$$

ماتریس یکانی

این بار ماتریس‌ها را در فضای «اعداد مختلط» (Complex Numbers) مورد بررسی قرار می‌دهیم.

یک ماتریس مربعی با مقادیر مختلط مثل $$U$$ را «ماتریس یکانی» (Unitary Matrix) می‌گویند، اگر «ترانهاده مزدوج» (Conjugate Transpose) آن با نماد $$U^*$$، معکوس آن نیز باشد. در این صورت خواهیم داشت.

$$\large {\displaystyle U^{*} U = U U^{*} = I } $$

رابطه ۳: تعریف ماتریس یکانی $$U$$

در رابطه بالا، منظور از $$I$$، همان «ماتریس همانی» (Identity Matrix) است.

در فیزیک، بخصوص در مکانیک کوانتمی، ماتریس «هرمیتی همسازه» (Hermitian Adjoint) با نشانه $$\dagger$$ مشخص می‌شود. در نتیجه گاهی ممکن است ماتریس یکانی را به صورت زیر معرفی کنند.

$$\large {\displaystyle U^{\dagger } U = U U^{ \dagger } = I } $$

مترادف ماتریس یکانی در اعداد حقیقی، «ماتریس متعامد» (Orthogonal Matrix) است، که یک ماتریس مربعی است که «ترانهاده» (Transpose) و «وارون ماتریس» (Inverse) آن با هم برابرند. یعنی برای ماتریس $$Q$$ با مولفه‌های حقیقی داریم:

$$ \large Q^T = Q^{-1} $$

یا به عبارت دیگر

$$ \large Q^T Q = Q Q^T = I $$

خواص ماتریس یکانی

برای هر ماتریس یکانی با ابعاد متناهی، می‌توان خصوصیات زیر را تحقیق کرد.

• دو بردار مختلط مثل $$x$$ و $$y$$ که در ماتریس $$U$$ ضرب داخلی شوند، روی ماتریس $$U$$، بی‌اثر هستند. یعنی داریم:

$$ \large \langle U x, U y \rangle = \langle x , y \rangle $$

• ماتریس $$U$$ نرمال است. یعنی $$U ^*U = U U^*$$. واضح است که $$U^*$$ همان ترانهاده مزدوج ماتریس $$U$$ است.
• ماتریس $$U$$، قابل قطری شدن است.
• دترمینان ماتریس $$U$$ به مانند ماتریس همانی برابر است با ۱

$$ \large |\det (U) | = 1 $$

• «فضای ویژه» (Eigenspaces) تولید شده توسط ماتریس یکانی، متعامد (Orthogonal) است.
• ماتریس $$U$$ را می‌توان به صورت زیر نمایش داد. در اینجا $$e$$، ماتریس نمایی و $$i$$ نیز عدد واحد موهومی است. همچنین $$H$$ نیز یک «ماتریس هرمیتی» (Hermitian Matrix) است.

همچنین اگر $$n$$ یک عدد صحیح باشد، مجموعه همه ماتریس‌های یکانی به همراه ضرب ماتریسی، تشکیل یک گروه (Group) داده که به «گروه یکانی» (Unitary Group) با نماد $$U(n)$$ معروف است.

نکته: توجه داشته باشید که هر ماتریس مربعی با اندازه یا «نرم اقلیدسی» (Euclidean Norm) برابر با ۱، میانگین دو ماتریس یکانی خواهد بود.

گزاره‌های هم‌ارز در مورد ماتریس یکانی

• ماتریس $$U$$، ماتریس یکانی است.
• ماتریس $$U^*$$، ماتریس یکانی است.
• ماتریس $$U$$ معکوس پذیر بوده و داریم $$U^{-1} = U^*$$.
• ستون‌های ماتریس $$U$$ پایه‌های متعامد از $$C^n$$ برای ضرب داخلی ماتریس‌ها تشکیل می‌دهند. یعنی:

$$ \large U^* U =  I $$

• سطرهای ماتریس $$U$$ پایه‌های متعامد از $$C^n$$ برای ضرب داخلی ماتریس‌ها تشکیل می‌دهند. یعنی:

$$ \large U U^* = I $$

• ماتریس $$U$$ متقارن نسبت به «نًرم عادی» (نُرم اقلیدسی) است. به این ترتیب داریم:

$$ \large || Ux ||_2 = ||x||_2 , \forall x \in C^n ,\;\;\; ||x||_2 = \sqrt{\sum_{i = 1}^n |x_i|^2} $$

• ماتریس $$U$$ یک ماتریس نرمال است که مقادیر ویژه آن روی دایره‌ای با شعاع واحد قرار گرفته‌اند.

ساختار ابتدایی ماتریس یکانی

فرض کنید می‌خواهیم یک ماتریس یکانی مرتبه ۲ ایجاد کنیم. ساختار اصلی برای چنین ماتریسی به شکل زیر است.

$$\large{\displaystyle U = { \begin{bmatrix} a & b \\ -e^{ i \varphi } b^{*} & e^{ i \varphi } a^{*} \\ \end{bmatrix}}, \qquad \left| a \right|^{2} + \left| b\right|^{2} = 1}$$

واضح است که ماتریس بالا به چهار پارامتر حقیقی وابسته است. قسمت حقیقی عدد $$a$$، قسمت حقیقی عدد $$b$$، مقدار نسبی بین $$a$$ و $$b$$، همچنین زاویه بین آن‌ها ($$\phi$$).

دترمینان این ماتریس به صورت زیر خواهد بود.

$$\large {\displaystyle \det(U) = e^{i \varphi }}$$

زیرگروهی از عناصر این ماتریس که دترمینان آن برابر با ۱ است را «گروه خاص یکانی» ( special unitary group) می‌نامند و با نماد $$SU(2)$$ مشخص می‌کنند.

ماتریس $$U$$ را که در رابطه بالا معرفی شد را به شکل دیگری نیز می‌توان نوشت.

$$ \large {\displaystyle U = e^{ i \varphi /2}{\begin{bmatrix} e^{ i \varphi _{1}} \cos \theta & e^{ i \varphi_{2}} \sin \theta \\ -e^{- i \varphi_{2}} \sin \theta & e^{ – i \varphi_{1}} \cos \theta \end{bmatrix}}} $$

واضح است که در رابطه بالا اگر $$\phi_1 = \psi + \Delta $$ و $$\phi_2 = \psi – \Delta $$ در نظر گرفته شوند، خواهیم داشت:

$$ \large {\displaystyle U = e^{ i \varphi /2} {\begin{bmatrix} e^{ i \psi } & 0 \\ 0 & e^{ – i \psi } \end{bmatrix}} {\begin{bmatrix} \cos \theta & \sin \theta \\ – \sin \theta & \cos \theta \\ \end{bmatrix}} {\begin{bmatrix} e^{ i \Delta } & 0 \\ 0 & e^{ – i \Delta } \end{bmatrix}} }$$

رابطه اخیر ارتباط بین دو ماتریس یکانی دو در دو و ماتریس متعامد دو در دو با زاویه $$\theta$$ را مشخص می‌کند. یک روش دیگر برای تفکیک ماتریس یکانی به شکل زیر نوشته می‌شود.

$$ \large {\displaystyle U = {\begin{bmatrix} \cos \alpha & – \sin \alpha \\ \sin \alpha & \cos \alpha \\ \end{bmatrix}} {\begin{bmatrix}e^{ i \xi } & 0 \\ 0 & e^{ i \zeta } \end{bmatrix}} {\begin{bmatrix} \cos \beta & \sin \beta \\ – \sin \beta & \cos \beta \\ \end{bmatrix}}} $$

نکته: روش‌های متعدد دیگری برای نمایش تفکیکی یا افراز شده از ماتریس یکانی براساس ماتریس‌های پایه وجود دارد.

همانطور که دیدید، ماتریس همانی و ماتریس یکانی از بعضی جنبه‌ها، شبیه یکدیگر عمل می‌کنند. به همین جهت شناخت خصوصیات آن‌ها در هر دو فضای حقیقی و مختلط، راه را برای انجام محاسبات ماتریسی باز می‌کند.

خلاصه و جمع‌بندی

در این مطلب از مجله فرادرس با دو ماتریس خاص یعنی ماتریس همانی و ماتریس یکانی در جبر خطی آشنا شدیم که در محاسبات مربوط به ضرب ماتریسی و مشخص کردن معکوس ماتریس‌ها، نقش مهمی دارند. در این بین «ماتریس همانی» (Identity Matrix)، به مانند عدد ۱ در عمل ضرب اعداد در جبر ماتریس‌ها نقش بازی می‌کند. از طرفی «ماتریس یکانی» (Unity Matrix)، نیز همین وظیفه را در «فضای هرمیتی» (Hermitian Space) دارد. خصوصیات و ویژگی‌های هر یک از ماتریس‌های همانی و یکانی نیز در متن گنجانده شد و مورد بحث قرار گرفت.