فرادرس
زاویه متمم چیست؟ — به زبان ساده + فیلم آموزش رایگان
زاویه‌های متمم، زاویه‌هایی هستند که جمع آن‌ها برابر با ۹۰ درجه می‌شود. این زاویه‌ها، اهمیت بسیار بالایی در روابط مثلثاتی دارند. در این مقاله، به معرفی زاویه متمم و نحوه محاسبه آن‌ها به همراه حل چندین مثال متنوع می‌پردازیم. علاوه بر این، انواع زاویه‌های متمم در شکل‌های مختلف را نیز مورد بررسی قرار می‌دهیم.
فیلم آموزشی زوایای متمم
انواع زاویه چه هستند؟
زاویه‌ها، انواع بسیار متنوعی دارند که بر اساس معیارهای مختلفی نظیر اندازه زاویه، رابطه آن‌ها با زاویه‌های دیگر و شکل هندسی، تقسیم‌بندی می‌شوند. بر این اساس، انواع زاویه عبارت هستند از:
- انواع زاویه بر اساس اندازه
- انواع زاویه بر اساس رابطه آن‌ها با زاویه‌های دیگر
- زاویه متمم
- زاویه مکمل
- زاویه مجاور
- جفت خطی
- متقابل به راس
- انواع زاویه بر اساس شکل هندسی
- زاویه داخلی
- زاویه خارجی
- زاویه مرکزی
- زاویه محاطی
- زاویه محیطی
زاویه متمم چیست؟
به هر دو زاویه که مجموع آن‌ها برابر با ۹۰ درجه باشد، دو زاویه متمم می‌گویند. مثال‌های بسیاری زیادی را از زاویه‌های متمم می‌توان بیان کرد. به عنوان مثال، دو زاویه ۳۰ و ۶۰ درجه، دو زاویه ۴۰ و ۵۰ درجه و دو زاویه ۴۵ درجه، زاویه‌هایی هستند که با یکدیگر، زاویه راست می‌سازند. از این‌رو، این جفت زاویه‌ها به عنوان زاویه‌های متمم شناخته می‌شوند.
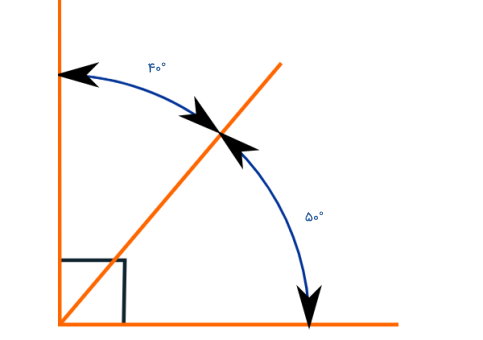
برای متمم بودن زاویه‌ها، نیازی به مشترک بودن ضلع‌های آن‌ها (مانند تصویر بالا) نیست. اگر مجموع دو زاویه جدا از هم نیز برابر با ۹۰ درجه باشد (تصویر زیر)، آن دو زاویه، متمم یکدیگر در نظر گرفته می‌شوند.
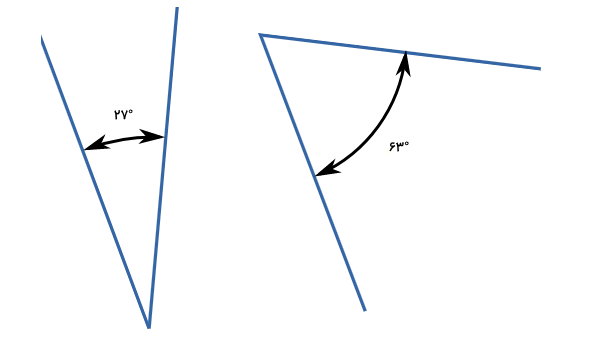
زاویه‌های متمم، یکی از انواع جفت‌زاویه‌ها هستند. از دیگر جفت‌زاویه‌ها می‌توان به زاویه‌های مکمل، زاویه‌های مجاور، جفت زاویه‌های خطی، زاویه‌های متقابل به راس و زاویه‌های متقاطع اشاره کرد. در صورت تمایل به یادگیری در مورد انواع زاویه‌ها، مطالعه مطلب «انواع زاویه چیست؟ — معرفی تمام زاویه ها — به زبان ساده» را به شما پیشنهاد میکنیم.
زاویه مکمل چه تفاوتی با زاویه متمم دارد؟
به هر دو زاویه که جمع آن‌ها برابر با ۱۸۰ درجه شود، دو زاویه مکمل گفته می‌شود. به عنوان مثال، دو زاویه قائمه، مکمل یکدیگر هستند. زاویه‌های مکمل نیز می‌توانند مانند زاویه‌های متمم، به هم چسبیده یا جدا از هم باشند. با قرار دادن دو زاویه مکمل در کنار یکدیگر (مانند تصویر زیر)، ضلع‌های غیر مشترک آن‌ها، یک خط راست (زاویه نیم‌صفحه) تشکیل می‌دهند.
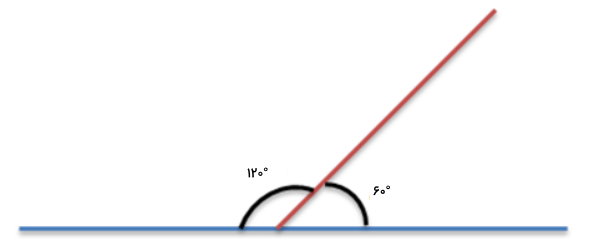
مثال ۱: محاسبه متمم یک زاویه
متمم زاویه ۱۲ درجه چند است؟
متمم زاویه ۱۲ درجه، زاویه‌ای است که با آن، تشکیل زاویه ۹۰ درجه می‌دهد. به عبارت دیگر، داریم:
۹۰° = زاویه دوم + زاویه اول = جمع زاویه‌های متمم
اندازه زاویه معلوم را درون رابطه بالا قرار می‌دهیم تا مکمل آن به دست بیاید:
۹۰° = زاویه دوم + °۱۲
۱۲° – ۹۰° = زاویه دوم
۷۸° = زاویه دوم
مثال ۲: اثبات وجود زاویه های متمم در گونیا
ثابت کنید که هر گونیا دارای دو زاویه متمم است.
گونیا، یک ابزار مثلث شکل اندازه‌گیری زاویه و تشخیص انواع زاویه است. این ابزار هندسی از یک گوشه با زاویه راست یا قائمه تشکیل می‌شود.
بر اساس قضیه مجموع زوایای داخلی مثلث، جمع سه زاویه گونیا، باید برابر با ۱۸۰ درجه شود:
۱۸۰° = زاویه سوم + زاویه دوم + زاویه اول
همیشه یکی از زاویه‌های گونیا، قائمه و برابر با ۹۰ درجه است. بنابراین، داریم:
۱۸۰° = زاویه سوم + زاویه دوم + °۹۰
۹۰° – ۱۸۰° = زاویه سوم + زاویه دوم
۹۰° = زاویه سوم + زاویه دوم
به عبارت دیگر، جمع دو زاویه دیگر گونیا، همواره برابر با ۹۰ درجه است. در نتیجه، هر گونیا، دو زاویه متمم دارد. برای یادگیری نحوه اندازه‌گیری زاویه‌ها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
مثال ۳: محاسبه دو زاویه متمم از روی نسبت آن‌ها
نسبت دو زاویه متمم، ۲ به ۳ است. هر کدام از زاویه‌ها، چند درجه هستند؟
دو زاویه α و β را در نظر بگیرید. نسبت این دو زاویه، ۲ به ۳ یا همان دو سوم است. با وجود اینکه اندازه دقیق هر زاویه را نمی‌دانیم، می‌توانیم اولین رابطه بین آن‌ها را به صورت زیر بنویسیم:
$$
\frac { \alpha } { \beta } = \frac { ۲ } { ۳ }
$$
بر اساس صورت مسئله، جمع این زاویه برابر با ۹۰ درجه می‌شود:
$$
\alpha + \beta = ۹۰ ^ { \circ }
$$
اکنون دو رابطه و دو مجهول داریم. در رابطه اول، زاویه β را به سمت دیگر می‌بریم:
$$
\alpha = \frac { ۲ } { ۳ } \beta
$$
به جای α در رابطه دوم، از عبارت بالا استفاده میکنیم:
$$
\frac { ۲ } { ۳ } \beta + \beta = ۹۰ ^ { \circ }
$$
$$
\frac { ۲ + ۳ } { ۳ } \beta = ۹۰ ^ { \circ }
$$
$$
\frac { ۵ } { ۳ } \beta = ۹۰ ^ { \circ }
$$
$$
\beta = ۹۰ ^ { \circ } \times \frac { ۳ } { ۵ }
$$
$$
\beta = \frac { ۲۷۰ ^ { \circ } } { ۵ }
$$
$$
\beta = ۵۴ ^ { \circ }
$$
اندازه یکی از زاویه‌ها برابر ۵۴ درجه است. بنابراین، اندازه زاویه دیگر از رابطه زیر به دست می‌آید:
$$
\alpha + ۵۴ ^ { \circ } = ۹۰ ^ { \circ }
$$
$$
\alpha = ۹۰ ^ { \circ } – ۵۴ ^ { \circ }
$$
$$
\alpha = ۳۶ ^ { \circ }
$$
در نتیجه، اندازه زاویه دیگر برابر با ۳۶ درجه است.
مثال ۴: محاسبه زاویه مکمل از روی متمم
نسبت دو زاویه متمم برابر با ۴ به ۵ است. مکمل زاویه بزرگ‌تر چیست؟
بخشی از مراحل حل این مثال، مشابه با مثال قبلی است. به این منظور، دو زاویه α و β را در نظر می‌گیریم. نسبت این دو زاویه، به صورت زیر نوشته می‌شود:
$$
\frac { \alpha } { \beta } = \frac { ۴ } { ۵ }
$$
مجموع α و β نیز برابر با ۹۰ درجه است:
$$
\alpha + \beta = ۹۰ ^ { \circ }
$$
رابطه اول را بر حسب α بازنویسی میکنیم:
$$
\alpha = \frac { ۴ } { ۵ } \beta
$$
سپس، این رابطه را درون رابطه دوم قرار می‌دهیم:
$$
\alpha + \beta = ۹۰ ^ { \circ }
$$
$$
\frac { ۴ } { ۵ } \beta + \beta = ۹۰ ^ { \circ }
$$
$$
\frac { ۴ + ۵ } { ۵ } \beta = ۹۰ ^ { \circ }
$$
$$
\frac { ۹ } { ۵ } \beta = ۹۰ ^ { \circ }
$$
$$
\beta = ۹۰ ^ { \circ } \times \frac { ۵ } { ۹ }
$$
$$
\beta = ۵۰ ^ { \circ }
$$
یکی از زاویه‌ها برابر با ۵۰ درجه است. بنابراین، زاویه دیگر برابر با ۴۰ درجه خواهد بود. در صورت سوال، مکمل زاویه بزرگ را از ما می‌خواهد.
۱۸۰° = زاویه مکمل + °۵۰
۵۰° – ۱۸۰° = زاویه مکمل
۱۳۰° = زاویه مکمل
مثال ۵: محاسبه زاویه های متمم از روی اختلاف اندازه
تفاضل دو زاویه متمم برابر با ۴۹ درجه است. اندازه زاویه هر دو زاویه را به دست بیاورید.
به منظور حل این مثال، دو زاویه α و β را در نظر می‌گیرم. بر اساس صورت مسئله، تفاضل این دو زاویه برابر با ۴۹ درجه است. رابطه مربوط به این تفاضل را می‌نویسیم:
$$
\alpha – \beta = ۴۹ ^ { \circ }\\
$$
رابطه مجموع زاویه‌های متمم نیز به صورت زیر نوشته می‌شود:
$$
\alpha + \beta = ۹۰ ^ { \circ }
$$
با استفاده از این دو رابطه و اصول حل دستگاه معادلات خطی، می‌توانیم اندازه α و β را به دست بیاوریم. به این منظور، رابطه‌های بالا را با هم جمع میکنیم:
$$
\begin{aligned}
& \alpha – \beta = ۴۹ ^ { \circ }\\
& \alpha + \beta = ۹۰ ^ { \circ } \\
& ———— \\
& \alpha + \alpha – \beta + \beta = ۴۹ ^ { \circ } + ۹۰ ^ { \circ }
\end{aligned}
$$
با این کار، به رابطه زیر می‌رسیم:
$$
\alpha + \alpha – \beta + \beta = ۴۹ ^ { \circ } + ۹۰ ^ { \circ }
$$
$$
۲ \alpha = ۱۳۹ ^ { \circ }
$$
$$
\alpha = \frac { ۱۳۹ ^ { \circ } } { ۲ }
$$
$$
\alpha = ۶۹/۵ ^ { \circ }
$$
اکنون، یکی از زاویه‌ها را داریم. متمم این زاویه برابر است با:
$$
۶۹/۵ ^ { \circ }+ \beta = ۹۰ ^ { \circ }
$$
$$
\beta = ۹۰ ^ { \circ } – ۶۹/۵ ^ { \circ }
$$
$$
\beta = ۲۰/۵ ^ { \circ }
$$
زاویه دوم برابر با ۲۰/۵ درجه است. دو زاویه ۶۹/۵ و ۲۰/۵ درجه، متمم یکدیگرند و تفاضل آن‌ها برابر با ۱۴۶ درجه می‌شود.
مثال ۶: تعیین زاویه از روی نسبت متمم به مکمل
نسبت متمم زاویه‌ای به مکمل آن برابر با یک‌پنجم است. اندازه این زاویه را به دست بیاورید.
ابتدا باید زاویه‌های مورد سوال را نامگذاری کنیم. فرض کنید، عنوان هر زاویه به صورت زیر است:
- α: زاویه مورد نظر
- β: متمم زاویه
- γ: مکمل زاویه
برای دو زاویه متمم داریم:
$$
\alpha + \beta = ۹۰ ^ { \circ }
$$
رابطه دو زاویه مکمل نیز عبارت است است:
$$
\alpha + \gamma = ۱۸۰ ^ { \circ }
$$
این دو رابطه را از هم کم میکنیم:
$$
\begin{aligned}
& \alpha + \gamma = ۱۸۰ ^ { \circ } \\
– \\
& \alpha + \beta = ۹۰ ^ { \circ } \\
& ———— \\
& \alpha – \alpha + \gamma – \beta = ۱۸۰ ^ { \circ } – ۹۰ ^ { \circ }
\end{aligned}
$$
حاصل تفریق دو رابطه بالا عبارت است از:
$$
\alpha – \alpha + \gamma – \beta = ۱۸۰ ^ { \circ } – ۹۰ ^ { \circ }
$$
$$
\gamma – \beta = ۹۰ ^ { \circ }
$$
با توجه به اطلاعات مسئله، نسبت β به γ به صورت زیر نوشته می‌شود:
$$
\frac { \beta } { \gamma } = \frac { ۱ } { ۵ }
$$
$$
\gamma = ۵ \beta
$$
عبارت بالا را درون تفاضل دو رابطه قرار می‌دهیم:
$$
۵ \beta – \beta = ۹۰ ^ { \circ }
$$
$$
۴ \beta = ۹۰ ^ { \circ }
$$
$$
\beta = \frac { ۹۰ ^ { \circ } } { ۴ }
$$
$$
\beta = ۲۲/۵ ^ { \circ }
$$
طی این مراحل، اندازه متمم زاویه مورد نظر را به دست آوردیم. این اندازه را دورن رابطه مجموع زوایای متمم قرار می‌دهیم:
$$
\alpha + ۲۲/۵ ^ { \circ } = ۹۰ ^ { \circ }
$$
$$
\alpha = ۹۰ ^ { \circ } – ۲۲/۵ ^ { \circ }
$$
$$
\alpha = ۶۷/۵ ^ { \circ }
$$
بنابراین، زاویه مورد سوال، برابر با ۶۷/۵ درجه است. مکمل این زاویه، ۱۱۲/۵ درجه می‌شود. با بررسی نسبت متمم به مکمل، به عدد ۵ (نسبت ذکر شده در صورت سوال) می‌رسیم.
زاویه های متمم در مثلثات
زاویه‌های متمم، کاربرد گسترده‌ای در تعریف روابط مثلثاتی دارند. بر اساس این روابط، سینوس یک زاویه، با کسینوس متمم آن برابری می‌کند. به عنوان مثال، سینوس زاویه ۳۰ درجه برابر با ۰/۵ یا یک‌دوم است. زاویه ۶۰ درجه، متمم زاویه ۳۰ درجه محسوب می‌شود. بنابراین، کسینوس زاویه ۶۰ درجه نیز برابر با یک‌دوم خواهد بود. درستی این قضیه را می‌توانید با استفاده از یک ماشین‌حساب بررسی کنید.
تصویر بالا را در نظر بگیرید. زاویه‌های α و β، متمم یکدیگر هستند. بنابراین، رابطه بین سینوس و کسینوس این زاویه‌ها، به صورت زیر نوشته می‌شود:
$$
\sin { \alpha } = \cos { \beta }
$$
$$
\sin { \beta } = \cos { \alpha }
$$
از دیگر رابطه‌های مثلثاتی بین زاویه‌های متمم، می‌توان به موارد زیر اشاره کرد:
برای حفظ کردن این روابط، به عنوان آن‌ها دقت کنید. معادل انگلیسی عبارت «متمم»، کلمه «Complementary» است. بخش ابتدایی این کلمه، به صورت «کُ» (Co) تلفظ می‌شود. این بخش، به صورت پیشوند در اول عبارت روابط مثلثاتی زاویه‌های متمم می‌آید. به عنوان مثال، سینوس به کُ-سینوس و تانژانت به کو-تانژانت تبدیل می‌شود. از این‌رو، سینوس یک زاویه، کُ-سینوس متمم آن است.
زاویه های متمم در چند ضلعی ها
زاویه‌های متمم را می‌توان در انواع چندضلعی‌ها مشاهده کرد. در این بخش، قصد داریم برخی از این موارد را مورد بررسی قرار دهیم.
زاویه‌های متمم در مثلث
مثلث، یک شکل سه‌ضلعی است که از سه راس تشکیل می‌شود. مجموع زوایای داخلی مثلث، برابر با ۱۸۰ درجه است. مثلث زیر را در نظر بگیرید. این مثلث، دو زاویه متمم با اندازه‌های ۳۰ و ۶۰ درجه دارد.
جمع زوایای داخلی مثلث از رابطه زیر به دست می‌آید:
۱۸۰° = زاویه سوم + زاویه دوم + زاویه اول
۱۸۰° = زاویه سوم + °۶۰ + °۳۰
۱۸۰° = زاویه سوم + °۹۰
۹۰° – ۱۸۰° = زاویه سوم
۹۰° = زاویه سوم
در نتیجه زاویه سوم مثلث برابر با ۹۰ درجه است. بنابراین، شکل بالا، یک مثلث قائم الزاویه را نمایش می‌دهد. به همین صورت می‌توانیم اثبات کنیم که تمام مثلث‌های قائم الزاویه، دارای دو زاویه متمم هستند.
زاویه‌های متمم در مربع و مستطیل
مربع و مستطیل، از انواع چهارضلعی‌ها هستند. این شکل‌های هندسی، از چهار راس با زاویه ۹۰ درجه تشکیل می‌شوند. به همین دلیل، مربع و مستطیل نمی‌توانند، دو زاویه متمم داشته باشند. البته، جمع زاویه‌های مجاور داخلی این دو شکل، همواره برابر با ۱۸۰ درجه (مکمل) می‌شود.
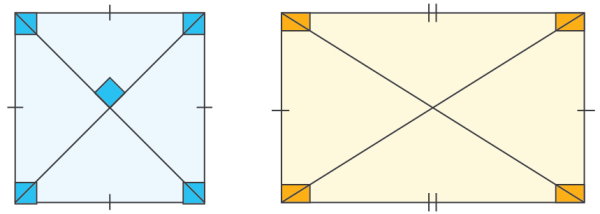
البته، در صورت رسم قطرهای مربع، چهار مثلث قائم الزاویه به وجود می‌آید. بنابراین، در هر یک از این چهار مثلث، دو زاویه متمم وجود خواهد داشت.
زاویه‌های متمم در لوزی
شکل لوزی، از نظر داشتن زاویه‌های متمم، تا حدودی به مربع شباهت دارد. لوزی‌ها، از دو زاویه تند (کمتر از ۹۰ درجه) و دو زاویه باز (بیشتر از ۹۰ درجه) تشکیل می‌شوند. به همین دلیل، جمع هیچ دو زاویه مجاور، برابر با ۹۰ درجه نخواهد شد. البته فقط در صورت وجود دو زاویه ۴۵ درجه روبه‌رویی، می‌توان زوایای متمم را در لوزی مشاهده کرد.
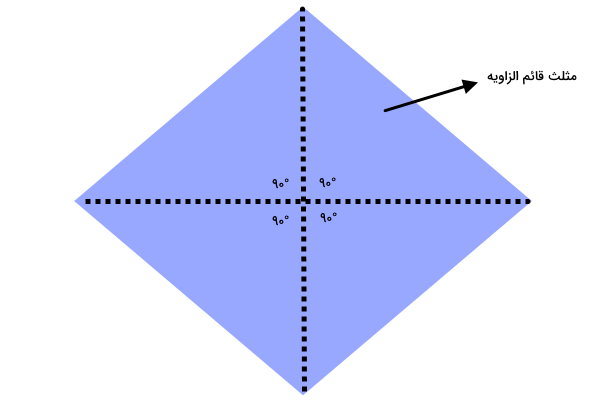
قطرهای لوزی بر هم عمود می‌شوند. به همین دلیل، در صورت رسم این قطرها، مانند مربع، چهار مثلث قائم الزاویه به وجود می‌آید. زاویه‌های غیر راست این مثلث‌ها، متمم یکدیگرند.
سوالات متداول در رابطه با زاویه های متمم
در این بخش، به برخی از سوالات پرتکرار در رابطه با زاویه‌های متمم به طور خلاصه پاسخ می‌دهیم.
تلفظ زاویه متمم چگونه است؟
زاویه متمم به صورت «زاویه مُتَمِّم» تلفظ می‌شود.
دو زاویه متمم یعنی چه ؟
دو زاویه متمم، یعنی دو زاویه‌ای که جمع آن‌ها برابر با ۹۰ درجه می‌شود.
زاویه متمم چند درجه است ؟
زاویه‌های متمم می‌توانند هر اندازه‌ای داشته باشند؛ به شرطی که مجموع آن با هم برابر با ۹۰ درجه شود.
تفاوت زاویه متمم و زاویه مکمل چیست؟
زاویه‌های مکمل، بزرگ‌تر از زاویه‌های متمم هستند. جمع دو زاویه مکمل برابر با ۱۸۰ درجه است.
کدام مثلث دو زاویه متمم دارد ؟
مثلث قائم الزاویه.
متمم زاویه ۳۰ درجه چند است ؟
۶۰ درجه.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «زاویه ها و انواع آن ها – هر آنجه باید بدانید» است. در ادامه، می‌توانید فهرست این مطالب را ببینید:
- زاویه چیست؟ — تعریف، انواع و اندازه گیری (+ فیلم آموزش رایگان)
- انواع زاویه چیست؟ — معرفی تمام زاویه ها — به زبان ساده
- راس زاویه چیست؟ — به زبان ساده + حل مثال تصویری
- زاویه حاده چیست؟ — به زبان ساده + حل مثال های متنوع تصویری
- زاویه باز چیست؟ — به زبان ساده + حل مثال های تصویری
- زاویه قائمه چیست؟ — به زبان ساده + حل مثال های تصویری
- زاویه مکمل چیست؟ — به زبان ساده + حل تمرین و مثال
- زاویه متمم چیست؟ — به زبان ساده + فیلم آموزش رایگان(همین مطلب)
- زاویه متقابل به راس چیست؟ — به زبان ساده + حل تمرین و مثال
- زاویه‌های مکمل و متمم در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- زاویه نیم‌صفحه و تعریف آن در هندسه — به زبان ساده
- زاویه محاطی چیست؟ — اثبات قضیه + حل تمرین و مثال های متنوع
- نیمساز چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- اندازه گیری زاویه با نقاله — به زبان ساده + مثال های تصویری
- اندازه گیری زاویه با گونیا — به زبان ساده + مثال های تصویری
