تمام فرمول های سینماتیک با مثال و تمرین
«سینماتیک یا حرکتشناسی» (Kinematic) شاخهای از فیزیک مکانیک است که به بررسی حرکت یک جسم بدون در نظر گرفتن عامل ایجاد کننده آن میپردازد. به این منظور، کمیتهای فیزیکی مختلفی در مسائل این حوزه بررسی میشوند که عبارتاند از مکان، زمان، جابجایی و مسافت، سرعت و شتاب. نحوه ارتباط این کمیتها با هم توسط فرمول های سینماتیک مشخص میشود.
- مبانی سینماتیک و انواع کمیتهای برداری و اسکالر را میآموزید.
- نحوه استفاده از فرمولهای اصلی سینماتیک در حل مسئله را یاد میگیرید.
- تفاوت حرکت خطی، زاویهای، سقوط آزاد و پرتابی را خواهید آموخت.
- فرمولهای مستقل از زمان، شتاب و نحوه انتخاب هر یک را یاد خواهید گرفت.
- مهارت محاسبه جابجایی، سرعت، شتاب و زمان را در سناریوهای مختلف کسب میکنید.
- روند استخراج سرعت و شتاب را از طریق مشتقگیری میآموزید.


در این مطلب از مجله فرادرس قصد داریم با شروع از سادهترین روابط، تمام فرمول های سینماتیک را با هم بررسی کنیم. همچنین توضیح میدهیم که کدام فرمول در چه نوع حرکتی بکار میرود و برای محاسبه چه کمیتی مناسب است. به علاوه، با حل مثال و ارائه تمرینهای مرتبط با هر فرمول، به شما کمک میکنیم تا درک جامعی از این مبحث بهدست آورید و در حل مسائل آن بهدرستی عمل کنید.
فرمول های سینماتیک
فرمول های سینماتیک که معادلات حرکت هم نامیده میشوند، برای پیدا کردن مکان جسم، مدت زمان حرکت آن، جابجایی و مسافت طی شده توسط جسم و یا در محاسبه کمیتهایی مانند سرعت، شتاب، تکانه و انرژی جنبشی بکار میروند. جدول زیر تمام فرمول های سینماتیک مربوط به حرکت خطی یک جسم را نشان میدهد:
| کمیت و نوع حرکت | فرمول |
| سرعت متوسط در حرکت سرعت ثابت | |
| معادله مکان - زمان در حرکت سرعت ثابت | |
| سرعت متوسط در حرکت شتاب ثابت | |
| شتاب متوسط در حرکت شتاب ثابت | |
| معادله سرعت - زمان در حرکت شتاب ثابت | |
| معادله مستقل از شتاب در حرکت شتاب ثابت | |
| معادله درجه دوم مکان - زمان در حرکت شتاب ثابت | |
| معادله مستقل از زمان در حرکت شتاب ثابت |
منظورمان از حرکت با سرعت ثابت حرکت جسمی است که اندازه و جهت سرعتش در طول حرکت تغییر نکند. به محض اینکه اندازه یا جهت سرعت جسم عوض شود، شتاب ایجاد میشود. در این حالت، حرکت جسم دیگر حرکت با سرعت ثابت محسوب نمیشود. همچنین زمانی که شتاب ایجاد شد، تا زمانی که اندازه و جهت شتاب ایجاد شده عوض نشود، حرکت با شتاب ثابت داریم. اما اگر یکی از این دو در مورد شتاب تغییر کند، حرکت با شتاب متغیر را خواهیم داشت که موضوع این مطلب نیست.
اگر به انواع حرکت در محیط اطراف خود دقت کرده باشید، حرکت یک جسم همیشه در راستای یک خط مستقیم نیست. گاهی مسیر حرکت جسم به شکل یک منحنی خواهد بود. در این شرایط فرمول های سینماتیک با متغیرهای جدیدی تعریف میشوند، در حالی که شکل فرمولها دقیقا شبیه به جدول بالا است. پیش از اینکه روابط مربوط به این نوع حرکت را معرفی کنیم، بهتر است ابتدا تفاوت دو نوع حرکت جسم را بهتر بشناسیم.
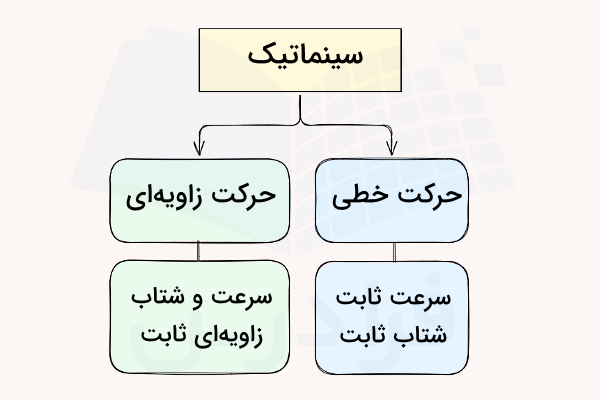
انواع حرکت در فیزیک
بطور کلی اجسام در فیزیک حرکتهای مختلفی دارند. ما در این نوشته به دو نوع «حرکت خطی» (Linear Motion) و «حرکت زاویهای» (Angular Motion) میپردازیم. حرکت خطی همان حرکت یک بعدی جسم در راستای یک مسیر مستقیم است، در حالی که در حرکت زاویهای، جسم حول یک محور ثابت حرکت میکند و در نتیجه مسیر آن بهصورت یک منحنی است.
در مورد تفاوتهای این دو نوع حرکت در بخشهای بعد بیشتر صحبت خواهیم کرد. جدول زیر تمام فرمول های سینماتیک مربوط به حرکت زاویهای یک جسم را نشان میدهد:
| نام کمیت | فرمول |
| سرعت زاویهای متوسط | |
| معادله زاویه - زمان | |
| شتاب زاویهای متوسط | |
| معادله سرعت زاویهای - زمان | |
| معادله مستقل از شتاب زاویهای | |
| معادله زاویه - زمان (درجه دو) | |
| معادله مستقل از زمان |
اینکه کدام فرمول در حل مسئله به شما کمک میکند، ممکن است گمراهکننده بنظر برسد. اما کافی است ابتدا دادههایی که در صورت سوال دارید را فهرست کنید، به این صورت که مقدار و جهت کدام پارامترها مشخص است و کدام متغیرها مجهول سوال هستند. سپس باید نوع حرکت را تشخیص دهید و با نگاه کردن به فرمول های سینماتیک، رابطه مناسب را انتخاب کنید. البته انتخاب دستگاه مختصات و قراردادی که در مورد جهتهای مثبت دارید، نیز مهم است.

دقت کنید گاهی مقدار یک کمیت در سوال به وضوح بیان نمیشود. اما میتوانید با توجه به توضیحات بیان شده در مورد مقدار آن کمیت تصمیمگیری کنید. برای مثال، معمولا اگر در مورد انداختن یک جسم اطلاعاتی داده نشود، سرعت اولیه آن صفر در نظر گرفته میشود. در ادامه پس از معرفی کمیتها، از سادهترین رابطه شروع میکنیم و تمام فرمولهای بالا را با مثال توضیح خواهیم داد.
سینماتیک چیست؟
سینماتیک بخشی از علم فیزیک است که به بررسی و مطالعه حرکت اجسام بدون در نظر گرفتن نیروها یا عوامل ایجاد کننده حرکت، میپردازد. اولین قدم برای اینکه فرمول های سینماتیک را بشناسیم و بتوانیم بهخوبی از آنها استفاده کنیم، درک مفهوم سینماتیک است. سینماتیک یا حرکتشناسی به مطالعه حرکت اجسام میپردازد.
حرکت جزء جداناپذیر زندگی ما است و ما پیوسته در حال مشاهده، تجربه، ایجاد و توقف حرکت هستیم. مطالعه کامل حرکت یک جسم در یک بازه زمانی مشخص اغلب بسیار پیچیده است. اما در این نوشته قصد داریم ببینیم حرکت در سادهترین نوع خود به چه صورت است و به سوالاتی مانند اینکه یک جسم در حال حرکت تا کجا پیش میرود، سرعت حرکت آن چقدر است یا حرکت آن چقدر طول میکشد، پاسخ دهیم. در این سوالات تلاشی برای درک عامل یا عوامل ایجاد کننده حرکت نمیشود و این نکته مهمی در سینماتیک است.
برای پاسخدهی به سوالات سینماتیک باید ابتدا متغیرهای مورد بررسی در این شاخه مشخص شوند. سپس با انجام آزمایشهای مختلف رابطه بین این متغیرها و اینکه چگونه با هم تغییر میکنند، تعیین شود. ارتباط بین متغیرهای مختلف سینماتیک توسط فرمول های سینماتیک مشخص میشود که در این مطلب از مجله فرادرس با تمام این فرمولها آشنا خواهید شد.
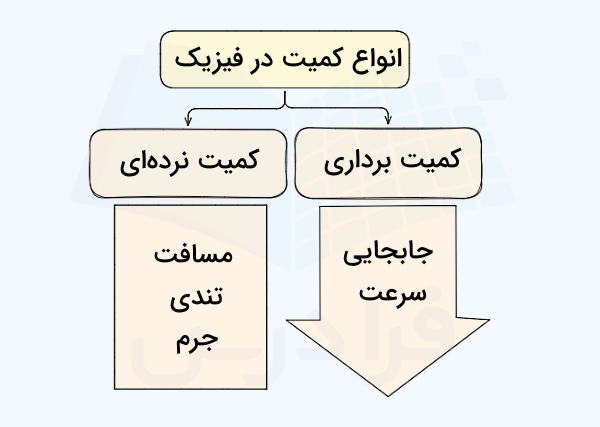
پیش از معرفی متغیرها و فرمول های سینماتیک، ابتدا خیلی کوتاه در مورد انواع متغیرها یا کمیتها صحبت میکنیم. احتمالا میدانید که کمیتهای فیزیکی از نظر اندازه و جهت، به دو گروه تقسیم میشوند:
- کمیتهای نردهای، عددی یا اسکالر: فقط اندازه دارند.
- کمیتهای برداری: هم اندازه دارند و هم جهت.
بنابراین وقتی یک کمیت اسکالر را اندازه میگیریم، فقط کافی است مقدار اندازهگیری شده را با یک عدد بیان کنیم. برای مثال کمیت عددی جرم که با نماد نشان داده میشود، را در نظر بگیرید. فرض کنید میخواهید جرم یک هندوانه را اندازهگیری کنید. در این صورت با استفاده از یک وسیله اندازهگیری مناسب یعنی ترازو، عددی مانند بهدست میآید.
اما در مورد کمیت برداری علاوه بر بیان مقدار عددی، جهت کمیت نیز باید مشخص شود تا اندازهگیری ما کامل شود. به همین دلیل در مورد کمیتهای برداری، انتخاب دستگاه مختصات مناسب مهم است. برای نمونه فرض کنید میخواهیم کمیت برداری نیروی کشش طناب () را توسط یک نیروسنج اندازهگیری کنیم. نیروسنج عددی مانند را نشان میدهد. اما این عدد برای بیان دقیق کمیت نیرو کافی نیست، بلکه عبارتهای یا که جهت منفی یا مثبت نیرو را شامل میشوند، بیان صحیح است. در بخش بعد نردهای یا برداری بودن تمام کمیتهای سینماتیک را مشخص خواهیم کرد.
مسیر یادگیری سینماتیک برای دانش آموزان با فرادرس
اگر دانشآموز هستید، یکی از بهترین روشها برای یادگیری انواع فرمول های سینماتیک این است که فیلمهای آموزشی تهیه شده در این زمینه را مشاهده کنید. در ادامه، لیستی از تمام دورههای آموزشی فرادرس با موضوع سینماتیک و بررسی انواع حرکت در مقطع متوسطه را برای شما قرار دادهایم:
- فیلم آموزش علوم تجربی نهم بخش فیزیک فرادرس
- فیلم آموزش فیزیک دهم فرادرس
- فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم فرادرس
- فیلم آموزش فیزیک دوازدهم سوالات امتحانات نهایی با حل تشریحی فرادرس
- فیلم آموزش فیزیک دوازدهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم نکته و حل تست کنکور فرادرس
- فیلم آموزش رایگان دینامیک و حرکت دایره ای فرادرس
- فیلم آموزش رایگان نمودار سرعت زمان فرادرس
مهم ترین کمیت های سینماتیک چه هستند؟
از نظر ریاضیاتی، حل مسائل سینماتیک شامل درک، محاسبه و اندازهگیری کمیتهایی است که در این بخش آنها را معرفی خواهیم کرد و در بخشهای بعد، رابطه بین این کمیتها را در قالب فرمول های سینماتیک تشریح میکنیم. جدول زیر انواع کمیتهای مربوط به حرکت خطی و مشخصات آنها را بهطور خلاصه نشان میدهد:
| کمیتهای سینماتیک خطی | واحد | نوع |
| مکان یا | متر () | برداری |
| جابجایی خطی یا | متر () | برداری |
| مسافت یا | متر () | عددی |
| زمان یا | ثانیه () | عددی |
| سرعت خطی یا | متر بر ثانیه () | برداری |
| تندی خطی یا | متر بر ثانیه () | عددی |
| شتاب خطی یا | متر بر مجذور ثانیه () | برداری |
| تکانه خطی یا | کیلوگرم متر بر مجذور ثانیه () | برداری |
| انرژی جنبشی خطی یا | ژول () | عددی |
همانطور که در ابتدای نوشته توضیح دادیم، در حرکت زاویهای کمیتهای جدیدی تعریف میکنیم که دارای مشخصات زیر هستند:
| کمیتهای سینماتیک زاویهای | واحد |
| زاویه یا | رادیان () |
| جابجایی زاویهای یا | رادیان () |
| زمان یا | ثانیه () |
| سرعت زاویهای یا | رادیان بر ثانیه () |
| شتاب زاویهای یا | رادیان بر مجذور ثانیه () |
| انرژی جنبشی زاویهای یا | ژول () |
در ادامه ابتدا راجعبه کمیتهای خطی و فرمولهای حاکم بر آنها توضیح خواهیم داد. سپس در بخشهای انتهایی مطلب، به توضیح کمیتهای زاویهای و فرمولهای مربوط به آن خواهیم پرداخت.

مکان، جابجایی و مسافت
اولین متغیرهایی که در بررسی فرمول های سینماتیک حرکت خطی مهماند، سه کمیت «مکان» (Position)، «جابجایی» (Displacement) و «مسافت» (Distance) هستند. پیش از اینکه به ادامه این مبحث بپردازیم، پیشنهاد میکنیم برای درک بهتر تعاریف این متغیرها و همچنین حل مسائل متنوع در این زمینه، فیلم آموزشی فیزیک ۱ دانشگاهی با رویکرد حل مساله فرادرس را که لینک آن در ادامه برای شما قرار داده شده است، مشاهده کنید:
شباهت این سه به هم بسیار زیاد است، چون هر سه از خانواده طول محسوب میشوند و همانطور که در جدول بخش قبل مشخص است، واحد یکسانی دارند. اما اگر دقت کنید نوع و نماد آنها در جدول متفاوت است. تفاوت این کمیتها بر اساس تعریفشان مشخص میشود:
- مکان: موقعیت فیزیکی جسم در فضا نسبت به مبدا دستگاه مختصات انتخابی است.
- جابجایی: تغییرات مکانی جسم در فضا است که با فرمول محاسبه میشود.
- مسافت: کل مسیر پیموده شده توسط جسم.
مکان
در یک حرکت خطی ساده، همواره جسم در یک بعد از فضا حرکت میکند که میتواند در راستای محور y، x یا z باشد. اگر فرض کنیم حرکت خطی ساده جسم در راستای محور افقی یا xها است، در این صورت از نماد برای نشان دادن مکان استفاده میکنیم. اما اگر حرکت خطی ساده ما در راستای قائم یا محور yها بود، میتوانیم مکان جسم را با نماد نشان دهیم.
همچنین در بررسی حرکت یک جسم، مهم است بدانیم در ابتدای حرکت جسم کجا قرار داشته است و در نهایت به چه نقطهای میرود. موقعیت فیزیکی ابتدایی جسم را مکان اولیه مینامیم که در متون مختلف با یا یا نشان داده میشود. به همین صورت، موقعیت فیزیکی نهایی جسم را مکان ثانویه یا مکان نهایی مینامیم که با یا یا نشان داده میشود.
جابجایی
اگر بخواهیم بدانیم موقعیت نهایی یک جسم نسبت به موقعیت اولیه آن چه تفاوتی دارد، باید جابجایی جسم را اندازهگیری کنیم. در یک حرکت خطی ساده، اگر مکان اولیه جسم و مکان نهایی آن باشد، در این صورت جابجایی جسم برابر میشود با:
در فرمول بالا، علامت دلتا (Δ) در کنار مکان یا x به معنای تغییرات یا اختلاف است. نکته مهم در مورد جابجایی این است که این کمیت برداری است، یعنی در محاسبه آن باید جهت در نظر گرفته شود.
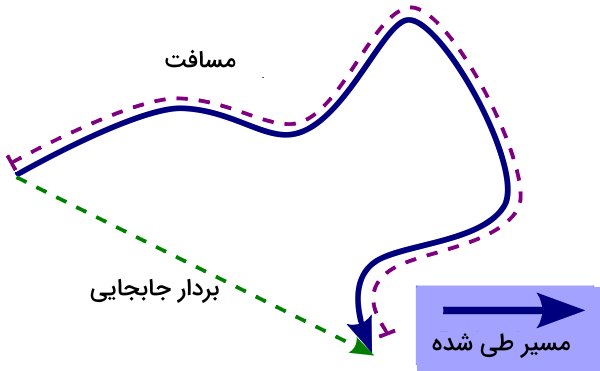
مسافت
دانستن تفاوت مسافت و جابجایی بسیار مهم است. گاهی اوقات ما به دنبال این هستیم که یک جسم در حرکت خود روی زمین چه مسیری را طی کرده است و میخواهیم طول کل آن مسیر را بهدست آوریم. به این منظور باید طول فواصل کوچکی که جسم در یک مسیر مشخص طی میکند را با هم جمع کنیم تا مسافت کل یا d را بهدست آوریم.
مسافت و جابجایی هر دو از جنس طول هستند و دارای واحد متر، اما جابجایی یک کمیت برداری است، در حالی که مسافت یک کمیت عددی محسوب میشود. شکل اول این بخش، تفاوت این دو را خیلی خوب نشان داده است. پس مهمترین وجه تفاوت این سه کمیت در این است که مکان و جابجایی هر دو کمیتهای برداری هستند، یعنی در مورد این دو متغیر جهت مهم است، در حالی که مسافت یک کمیت اسکالر است که فقط اندازه آن مهم است.
مثال
فرض کنید مسیر مجاز برای پیادهروی در یک منطقه از نقطه تا متر در راستای مثبت محور xها مشخص شده است. اگر از نقطهای با موقعیت شروع به حرکت در راستای مثبت محور xها کرده باشید، تا انتهای مسیر پیش بروید و سپس به موقعیت اولیه خود بازگردید، مکان اولیه، مکان نهایی، جابجایی و کل مسافت طی شده خود را مشخص کنید:
پاسخ
دقت کنید در ابتدای حرکت، در موقعیت قرار داریم. پس مکان اولیه میشود:
موقعیت نهایی طبق صورت سوال چون گفته شده به محل اولیه خود بازگشتهاید، همان مکان اولیه است، صرفنظر از اینکه چه مسیری پیش از آن طی شده است:
بنابراین جابجایی برابر است با:
اما مسافت طی شده در این حرکت برابر است با:
پس در این حرکت با اینکه راه رفتهاید، اما در واقع جابجایی شما صفر بوده است.
زمان
یکی از مهمترین کمیتهایی که در فرمول های سینماتیک وجود دارد و گاهی در برخی از مسائل حتی به دنبال محاسبه آن هستیم، زمان است. زمان در سینماتیک ممکن است در قالب لحظه یا بازه زمانی مطرح شود. برای مثال ممکن است بگوییم جسمی در زمان اولیه در مکان اولیه و در زمان ثانویه یا نهایی در مکان نهایی است. در این جمله، موقعیت مکانی جسم در دو لحظه مشخص شده است.
اگر بخواهیم اختلاف این دو لحظه یا بازه زمانی که طی آن جسم حرکت کرده است را بررسی کنیم، باید کمیتی به نام اختلاف زمانی یا را به شکل زیر بهدست آوریم:
بیان میکند که یک رویداد چقدر طول کشیده است.
سرعت متوسط و تندی
در مسائل حرکتشناسی، اغلب دنبال این هستیم که بدانیم میزان سریع بودن حرکت یک جسم چطور اندازهگیری میشود. در فیزیک برای اینکه ببینیم یک جسم چقدر سریع است، باید تغییر مکان آن را در طول زمان بررسی کنیم. بنابراین سرعت یا Velocity که با v نمایش داده میشود، برابر است با آهنگ تغییرات یا نرخ جابجایی در طول زمان:
سرعت بالا را سرعت متوسط مینامیم، چون برای یک بازه زمانی محاسبه شده است. طبق رابطه بالا و با توجه به اینکه واحد جابجایی متر و واحد زمان ثانیه است، واحد سرعت متر بر ثانیه خواهد بود. بنابراین وقتی که میگوییم سرعت جسمی است، مفهوم آن این است که این جسم در هر ثانیه جابجا میشود. البته باید دقت کنید که سرعت یک کمیت برداری است، یعنی زمانی که میگوییم سرعت جسمی است، باید جهت آن را نیز مشخص کنیم.

علت برداری بودن سرعت این است که در محاسبه آن از کمیت برداری جابجایی استفاده میشود. سرعت متوسط یا را میتوانیم با میانگینگیری از دو سرعت اولیه و نهایی نیز محاسبه کنیم. در بخشهای بعد خواهید دید که از این سرعت متوسط میتوانیم برای محاسبه مسافت طی شده در حرکت با شتاب ثابت استفاده کنیم:
شکل عددی یا اسکالر سرعت، تندی یا Speed نامیده میشود. نمایش تندی با نماد s است. تفاوت تندی و سرعت در جهت است، تندی جهت ندارد، در حالی که سرعت دارای جهت است. بهعبارت دیگر میتوانیم سرعت را مجموع تندی و جهت در نظر بگیریم. علت عددی بودن کمیت تندی این است که در محاسبه آن بهجای جابجایی از مسافت استفاده میشود:
واحد تندی مانند واحد سرعت متر بر ثانیه است. بنابراین در کاربرد فرمول های سینماتیک، باید به تفاوت تندی و سرعت کاملا دقت کنید.
شتاب متوسط
پس از سرعت، شتاب یکی دیگر از مهمترین کمیتهای سینماتیک است. اغلب هدف ما از کاربرد فرمول های سینماتیک، محاسبه سرعت یا شتاب حرکت جسم و تشخیص نوع حرکت آن است. اگر سرعت حرکت جسم تغییر کند، چه از نظر اندازه و چه از نظر جهت، حرکت جسم شتابدار خواهد شد. پس با توجه به اینکه شتاب در نتیجه تغییرات سرعت ایجاد میشود، میتوانیم فرمول زیر را برای آن بنویسیم:
در واقع شتاب متوسط یک جسم برابر است با نرخ یا آهنگ تغییرات سرعت آن در طول زمان و با نماد a نشان داده میشود. چون واحد سرعت متر بر ثانیه است و طبق رابطه بالا این واحد بر واحد زمان یعنی ثانیه تقسیم میشود، پس واحد شتاب معادل است با متر بر مجذور ثانیه. برای مثال اگر شتاب جسمی و با علامت مثبت محاسبه شود، یعنی حرکت آن جسم در راستای مثبت محور انتخابی حرکت با شتاب ثابت است (چون عدد عدد ثابتی است) و سرعت آن نیز پیوسته در حال زیاد شدن با گذر زمان است.
نکته: دقت کنید شتاب از محاسبه تغییرات سرعت بهدست میآید نه تغییرات تندی. اگر در فرمول شتاب به جای سرعت از تندی استفاده کنیم، در این صورت چون تغییر جهت سرعت را در نظر نگرفتهایم، ممکن است فرمول های سینماتیک اشتباهی را بکار ببریم.
یکی دیگر از کمیتهای مهم در سینماتیک انرژی جنبشی است که نحوه محاسبه آن در حرکت خطی و زاویهای متفاوت است. پیشنهاد میکنیم برای حل مسائل مختلف در زمینه کاربرد فرمول انرژی جنبشی خطی به مطلب «فرمول انرژی جنبشی چیست؟ – به زبان ساده با مثال و تمرین» از مجله فرادرس مراجعه کنید.
معادله مکان - زمان (حرکت با سرعت ثابت)
اولین فرمولهایی که در بخش اول این مطلب بهعنوان فرمول های سینماتیک معرفی کردیم، فرمول سرعت متوسط و معادله مکان - زمان هستند. گفتیم که اگر جسمی از مکان اولیه و در زمان شروع به حرکت کند و در زمان به مکان برسد، در این صورت سرعت متوسط و ثابت جسم از فرمول زیر بهدست میآید:
- : سرعت متوسط و ثابت جسم بر حسب متر بر ثانیه ()
- : جابجایی جسم بر حسب متر ()
- : مدت زمان حرکت جسم بر حسب ثانیه (s)
حالا اگر این فرمول را باز کنیم، میتوانیم آن را بهصورت زیر بنویسیم:
میتوانیم بهجای از استفاده کنیم تا معادلات حرکت شکل پیچیدهای به خود نگیرند. اما باید دقت کنید منظور ما از در فرمول زیر، همان بازه زمانی بین دو زمان اولیه و نهایی در حرکت با سرعت ثابت است:
به رابطه بالا معادله مکان - زمان گفته میشود که برای محاسبه مکان نهایی جسم در حرکت با سرعت ثابت بکار میرود. دقت کنید فرمول بالا را به شکل زیر هم میتوان نشان داد:
به حرکت با سرعت ثابت، حرکت یکنواخت هم گفته میشود.
مثال
فرض کنید اگر سکهای را داخل یک چاه رها کنید، مسافت طی شده آن طبق رابطه بر حسب متر بهدست میآید که در آن مدت زمان بر حسب ثانیه است. اگر صدای آب پس از رها کردن سکه شنیده شود و سرعت صوت برابر باشد با ، عمق چاه را محاسبه کنید:
پاسخ
برای حل این سوال، ابتدا معادله مکان - زمان را به شکل زیر مینویسیم:
اگر بخواهیم معادله بالا را در مورد صوت بکار ببریم، باید ببینیم صوت با سرعت ثابت در چه زمانی عمق چاه را طی کرده است. اگر عمق چاه را و مدت زمانی که صوت این فاصله را طی میکند، در نظر بگیریم، معادله مکان - زمان بالا خواهد شد:
حالا اگر مدت زمان لازم برای رسیدن سکه به ته چاه را بگیریم، در این صورت طبق رابطه صورت سوال داریم:
با مقایسه این رابطه و رابطه قبل، به تساوی زیر دست پیدا میکنیم:
از طرفی طبق صورت سوال، میدانیم کلا سه ثانیه زمان لازم است تا بلافاصله بعد از رها شدن سکه، صدای آن به ابتدای چاه برسد. پس بین این سه زمان رابطه زیر برقرار است:
حال میتوانیم این مقدار را در رابطه بالا جایگذاری کنیم:
پس از سادهسازی خواهیم داشت:
با حل معادله درجه دوم بالا و اینکه زمان نمیتواند منفی باشد، زمان موردنظر بهدست خواهد آمد:
با داشتن این زمان و قرار دادن آن در اولین رابطه، عمق چاه برابر میشود با:
معادله سرعت - زمان (حرکت با شتاب ثابت)
در این بخش میخواهیم ببینیم اگر سرعت جسم تغییر کند، فرمول های سینماتیک به چه صورت خواهد شد. فرض کنید جسمی در زمان دارای سرعت و در زمان دارای سرعت باشد. چون با گذشت زمان سرعت دیگری داریم که با سرعت اولیه یکی نیست، پس نمیتوانیم این حرکت را سرعت ثابت در نظر بگیریم. تغییرات سرعت، شتاب متوسط و ثابتی ایجاد میکند که برابر است با:
- : شتاب متوسط و ثابت جسم بر حسب متر بر مجذور ثانیه ()
- : تغییرات سرعت جسم بر حسب متر بر ثانیه ()
- : مدت زمان حرکت جسم بر حسب ثانیه (s)
گفتیم شتاب همان تغییرات سرعت است. این تغییر شامل یکی از این سه حالت زیر خواهد شد:
- مقدار عددی دو سرعت و برابر است و جهتهای مختلفی دارند.
- مقدار عددی دو سرعت و برابر نیست و جهتهای یکسانی دارند.
- مقدار عددی دو سرعت و برابر نیست و جهتهای مختلفی دارند.
حالا اگر به فرمول شتاب متوسط بازگردیم و آن را مثل بخش قبل بازنویسی کنیم، خواهیم داشت:
باز هم را در نظر میگیریم تا در نهایت به معادله سرعت - زمان برای حرکت با شتاب ثابت برسیم:
دقت کنید فرمول بالا را به شکل زیر هم میتوان نشان داد:
مثال
فرض کنید شخصی با جرم و با سرعت در حال اسکی روی یک سطح شیبدار به سمت پایین است که ناگهان میافتد و شروع به سر خوردن روی سطح میکند. چنانچه دقیقا بعد از افتادن، سرعت شخص به برسد، شتاب شخص در هنگام لیز خوردن چقدر است؟ مدت زمان لیز خوردن شخص تا لحظهای که روی زمین به سکون میرسد، چقدر است؟
پاسخ
ابتدا باید ببینیم چه دادههایی در صورت سوال مشخص شده است:
برای بهدست آوردن شتاب شخص، کافی است معادله سرعت - زمان برای حرکت با شتاب ثابت را بنویسیم:
همانطور که پیشبینی میشد، شتاب شخص باید منفی باشد، چون در حال لیز خوردن به سمت سطح زمین است و سرعت نهایی آن کمتر از سرعت اولیه شده است. در بخش دوم این مثال، کل مدت زمان لیز خوردن شخص خواسته شده است. پس باید شروع لیز خوردن را با سرعت اولیه و انتهای لیز خوردن را با سرعت نهایی صفر در نظر بگیریم. از طرفی در بخش قبل، شتاب لیز خوردن محاسبه شد. پس کافی است مجددا از معادله سرعت - زمان استفاده کنیم، با این تفاوت که در اینجا شتاب را داریم و مدت زمان مجهول مسئله است:
فرمول مستقل از شتاب (حرکت با شتاب ثابت)
یکی دیگر از فرمول های سینماتیک که برای محاسبه مکان یا موقعیت نهایی یک جسم در حال حرکت با شتاب ثابت بکار میرود، فرمول زیر است:
- : سرعت نهایی یا ثانویه جسم بر حسب متر بر ثانیه ()
- : سرعت اولیه جسم بر حسب متر بر ثانیه ()
- : مکان نهایی یا ثانویه جسم بر حسب متر ()
- : مکان اولیه جسم بر حسب متر ()
- : مدت زمان حرکت جسم با شتاب ثابت بر حسب ثانیه (s)

رابطه بالا زمانی استفاده میشود که جسم در حال حرکت با شتاب ثابت است و مکان اولیه، سرعت اولیه، سرعت ثانویه و مدت زمان حرکت آن کاملا مشخص هستند. دقت کنید با اینکه حرکت جسم با شتاب ثابت است، در این فرمول هیچ اثری از شتاب یا a نمیبینیم و به همین دلیل آن را فرمول مستقل از شتاب مینامیم. اما چون دو نوع سرعت در فرمول داریم. پس میتوانیم نتیجهگیری کنیم که سرعت عوض شده و شتاب داریم.
بنابراین اگر سایر پارامترهای مسئله مشخص باشند، حتی در حرکت شتاب ثابت، بدون داشتن شتاب میتوان مکان نهایی جسم را با این فرمول محاسبه کرد. اگر از فرمول جابجایی به شکل استفاده کنیم، شکل سادهتر رابطه بالا خواهد شد:
دقت کنید اگر حرکت جسم در راستای محور x نباشد، برای مثال در راستای محور y یا z، در این صورت تمام xها در روابط بالا با y یا z جایگزین میشوند.
مثال
در مثال بخش قبل، شخص چه مسافتی را روی سطح پس از افتادن پیموده است؟
پاسخ
اولین قدم برای حل سوال نوشتن دادههای صورت سوال است:
مسافت همان مقدار عددی یا اندازه جابجایی است. پس باید دنبال فرمولی از مجموعه فرمول های سینماتیک باشیم که علاوه بر کمیتهای بالا، جابجایی را داشته باشد. مناسبترین انتخاب، فرمول زیر است:
میتوانیم بهجای از استفاده کنیم. با عددگذاری خواهیم داشت:
پس مسافت بهدست آمد. دقت کنید علامت قدر مطلق به معنای اندازه جابجایی است. دیدید که برای محاسبه مسافت و شتاب در بخش قبل، فقط از فرمول های سینماتیک استفاده کردیم و نیازی به رسم نیروهای وارد بر شخص روی سطح شیبدار یا کاربرد کمیت جرم نبود.
معادله درجه دوم مکان - زمان (حرکت با شتاب ثابت)
کاربرد این فرمول از فرمول های سینماتیک شبیه به فرمول بخش قبل است، اما تفاوت در اینجا است که در این رابطه پارامتر شتاب را داریم. اگر دادههای سوال شما شامل مکان اولیه، سرعت اولیه، سرعت ثانویه و مدت زمان حرکت باشد اما شتاب را نداشته باشید، باید از فرمول بخش قبل استفاده کنید. اما اگر شتاب را به همراه مکان اولیه، سرعت اولیه و مدت زمان حرکت دارید ولی سرعت نهایی جسم مشخص نیست، فرمول زیر در حل مسئله به شما کمک خواهد کرد:
- : سرعت اولیه جسم بر حسب متر بر ثانیه ()
- : مکان نهایی یا ثانویه جسم بر حسب متر ()
- : مکان اولیه جسم بر حسب متر ()
- : مدت زمان حرکت جسم با شتاب ثابت بر حسب ثانیه (s)
- : شتاب ثابت جسم بر حسب متر بر مجذور ثانیه ()
همچنین با استفاده از فرمول جابجایی مشابه بخشهای قبل، میتوانید فرمول بالا را سادهتر کنید:
مثال ۱
اگر موشکی در فضا با سرعت در حال حرکت باشد، سپس با سوزاندن سوخت، شتاب ثابتی به میزان کسب کند، پس از مدت زمان چه مسافتی پیموده است؟
پاسخ
در این سوال سرعت اولیه موشک همراه با شتاب ثابت و مدت زمان حرکت آن با این شتاب، داده شده است. پس کافی است از فرمول زیر استفاده کنیم تا مسافت طی شده توسط موشک که معادل است، محاسبه شود:
مثال ۲
اتومبیلی از موقعیت سکون شروع به حرکت میکند و طی مدت زمان ، شتابی به اندازه بهدست میآورد. سپس به مدت دیگر با سرعت ثابت حرکت میکند. مسافت طی شده توسط این اتومبیل از زمان شروع به حرکت چقدر است (فرض کنید در تمام این مدت حرکت اتومبیل فقط در یک راستا بوده است)؟
پاسخ
جهت پاسخدهی به این سوال بهتر است آن را به دو بخش تقسیم کنیم (طبق شکل زیر). بخش اول مسافتی است که اتومبیل در حین شتاب گرفتن طی میکند و بخش دوم، مسافتی است که اتومبیل با سرعت ثابت حرکت میکند تا به مقصد برسد. ضمن اینکه در سوال ذکر شده است حرکت از حالت سکون شروع میشود، بنابراین میتوانیم در نظر بگیریم.
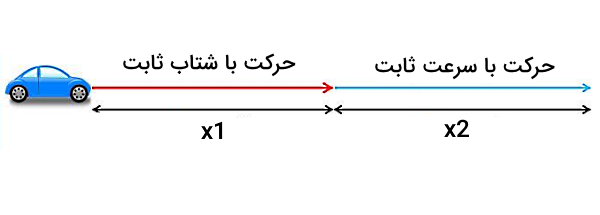
در بازه زمانی اول که حرکت شتابدار است، دادههای مسئله ما به شکل زیر است:
پس میتوانیم از معادله درجه دوم مکان - زمان برای پیدا کردن مکان نهایی اتومبیل در این بازه زمانی استفاده کنیم. کافی است مقادیر بالا را در آن جایگذاری کنیم:
گفتیم مسافت معادل مسیری است که جسم میپیماید. در این سوال بهجای ، مسافت بخش اول را با نشان میدهیم که برابر است با اختلاف مکان نهایی اتومبیل و مکان اولیه آن:
پس مشخص شد در بخش اول اتومبیل چه مسافتی را طی کرده است. حالا میرویم سراغ بخش دوم حرکت که با سرعت ثابت انجام میشود. معادله مکان - زمان در حرکت با سرعت ثابت به ما کمک میکند تا جابجایی اتومبیل در این بخش را محاسبه کنیم:
اما دادههایی که داریم به شکل زیر هستند:
یعنی سرعت را نداریم. اگر دقت کنید در بخش اول، اتومبیل با سرعت صفر شروع به حرکت کرده است و طی مدت زمان مشخصی شتاب میگیرد. اگر سرعت نهایی در بخش اول را پیدا کنیم، این سرعت معادل همان سرعت ثابتی است که اتومبیل در بخش دوم با آن به حرکت خود را ادامه میدهد. از فرمول شتاب متوسط میتوانیم سرعت نهایی بخش اول را محاسبه کنیم:
با در نظر گرفتن ، خواهیم داشت:
حالا میتوانیم دادههایی که داریم را در معادله مکان - زمان قرار دهیم:
اما دقت کنید مسافت این بخش را میخواهیم که اگر آن را با نشان دهیم، داریم:
پس کل مسافت طی شده توسط اتومبیل در این دو بخش برابر میشود با:
فرمول مستقل از زمان (حرکت با شتاب ثابت)
در نهایت به بررسی آخرین فرمول از مجموعه فرمول های سینماتیک میپردازیم که برای محاسبه سرعت نهایی یا ثانویه جسم طی حرکت با شتاب ثابت بکار میرود. اگر مقدار سرعت اولیه جسم، شتاب و جابجایی آن مشخص باشد، حتی با نداشتن مدت زمان حرکت جسم میتوانیم سرعت نهایی آن را با فرمول زیر پیدا کنیم:
- : سرعت نهایی یا ثانویه جسم بر حسب متر بر ثانیه ()
- : سرعت اولیه جسم بر حسب متر بر ثانیه ()
- : جابجایی جسم بر حسب متر ()
- : شتاب ثابت جسم بر حسب متر بر مجذور ثانیه ()
همچنین اگر فرمول جابجایی را در مورد استفاده کنیم، رابطه زیر را خواهیم داشت:
بنابراین اگر مقادیر سرعت اولیه، جابجایی و شتاب مشخص بودند، از فرمول مستقل از زمان به شکل بالا استفاده میکنیم تا سرعت نهایی حرکت جسم پیدا شود. اما اگر بهجای جابجایی، مدت زمان حرکت را داشتیم، معادله سرعت - زمان از فرمول های سینماتیک سرعت نهایی را محاسبه میکند.
مثال ۱
شناگری منتظر سیگنال شروع حرکت است و با دیدن سیگنال، داخل آب شیرجه زده و با سرعت صفر شروع به شنا میکند. اگر شناگر آنقدر شتاب بگیرد که به سرعت برسد، شتاب و جابجایی او در این بازه که به اندازه طول کشیده است، چقدر است؟

پاسخ
برای محاسبه شتاب با داشتن سرعت اولیه صفر طبق سوال، سرعت نهایی و بازه زمانی، بهترین فرمول معادله سرعت - زمان است:
حالا با داشتن شتاب، میتوانیم جابجایی را با فرمول مستقل از زمان محاسبه کنیم:
مثال ۲
فرض کنید میخواهید روی سطح شیبداری مطابق شکل زیر اسکی کنید. با شروع از حالت سکون در بالای سطح، اگر با شتاب روی سطح حرکت کنید و با سرعت به پایین آن برسید، این سطح چه ارتفاعی از سطح زمین دارد؟

پاسخ
برای اینکه بتوانیم ارتفاع سطح را محاسبه کنیم، باید ضلع قائم مثلث قائمالزاویه در شکل را پیدا کنیم. اما با توجه به فرمول های سینماتیک، ما فقط میتوانیم وتر این مثلث را که معادل با مسافت طی شده توسط شخص است، محاسبه کنیم. پس ابتدا این کمیت را با فرمول مستقل از زمان بهدست میآوریم:
حالا میتوانیم از زاویه مثلث و نسبت مثلثاتی سینوس این زاویه استفاده کنیم. میدانیم سینوس یک زاویه در مثلث قائمالزاویه برابر است با نسبت اندازه ضلع مقابل به آن زاویه به اندازه وتر مثلث. پس اگر ارتفاع سطح را h در نظر بگیریم، برای سینوس زاویه ۳۰ درجه در این مثلث داریم:
تمرین
حرکت سقوط آزاد
سقوط آزاد یک حرکت خطی یک بعدی است که فقط در راستای عمودی (در راستای محور قائم یا محور y) انجام میشود، پس جسم فقط تحت تاثیر شتاب جاذبه زمین قرار دارد. از آنجا که نیروی جاذبه زمین شتاب ثابتی دارد ()، پس سقوط آزاد یک حرکت با شتاب ثابت محسوب میشود.

در این بررسی از اثر مقاومت هوا یا اصطکاک صرفنظر میکنیم. طبق شکل بالا، توپی از ارتفاع مشخصی به اندازه رها میشود. رها شدن به معنای این است که سرعت اولیه توپ صفر است. همچنین مقدار شتاب جاذبه روی زمین برابر با مقدار ثابتی است که گفتیم، در حالی که اگر روی ماه باشیم شتاب جاذبه زمین کاهش مییابد. بنابراین ثابت در نظر گرفتن مقدار g روی زمین، برای این است که تا حد امکان حل مسائل فیزیکی ساده شود.
حالا اگر مکان اولیه توپ در دست شخص را و مکان نهایی توپ روی زمین را در نظر بگیریم، واضح است که جابجایی توپ در این سقوط آزاد برابر است با:
دقت کنید چون جهت مثبت محور عمودی را به سمت بالا در نظر گرفتهایم، پس جابجایی منفی میشود. تمام فرمولهایی که در مورد سینماتیک توضیح دادیم، برای سقوط آزاد هم برقرار هستند. فقط کافی است بهجای x از y استفاده کنیم و را اعمال کنیم:
در نوشتار بالا، دقیقتر این است که سرعتها را نیز با اندیس y بهصورت مشخص کنیم. اما چون در معادلات ابتدای بخش برای حرکت در راستای محور x چنین اندیسهایی به شکل استفاده نکردیم، در اینجا نیز سرعتها بدون اندیس نوشته شدهاند. با توجه به اینکه حرکت در راستای قائم است و در معادلات y داریم، مشخص است که راستای سرعت نیز در همین جهت است. برای اینکه با مسائل سقوط آزاد بیشتر آشنا شوید، به مثال زیر دقت کنید.
مثال ۱
فرض کنید ماشین حساب شما از ارتفاع روی زمین میافتد. سرعت ماشین حساب را در لحظه برخورد با زمین محاسبه کنید:
پاسخ
در اولین قدم باید اطلاعات مسئله را مشخص کنیم. افتادن ماشین حساب روی زمین بدون هیچ سرعت اولیهای انجام شده است. بنابراین . اگر سطح زمین را مبدا مختصات در نظر بگیریم و جهت مثبت محور y را به سمت بالا انتخاب کنیم، در این صورت مکان اولیه ماشین حساب برابر است با . مکان نهایی یا ثانویه روی سطح زمین است که با توجه به مبدا انتخابی ما میشود: .
بنابراین جابجایی ماشین حساب در این سقوط آزاد برابر است با:
از طرفی افتادن هر جسمی روی زمین بدون اعمال هیچ نیروی دیگری، در نتیجه نیروی وزن جسم و اثر جاذبه زمین است. بنابراین در این حرکت، جسم با شتاب ثابتی برابر با شتاب جاذبه زمین به سطح زمین میرسد. جهت شتاب جاذبه زمین به سمت زمین یا پایین است. بنابراین با در نظر گرفتن اختلاف علامت بین جهت شتاب و جهت مثبت محور y، خواهیم داشت:
پس مقدار سه کمیت در سوال مشخص است و سرعت نهایی یا مجهول مسئله است. با توجه به اینکه شتاب را داریم و زمان مشخص نیست، میتوانیم فرمول مستقل از زمان را برای حل سوال بنویسیم و عددگذاری کنیم:
دقت کنید بین دو جواب بالا، باید سرعتی که دارای علامت منفی است را در نظر بگیریم. چون جهت سرعت در لحظه برخورد با زمین به سمت پایین است.
مثال ۲
اگر کلیدهای خود را از ارتفاع رها کنید، چقدر طول میکشد تا به زمین برسند؟

پاسخ
چون کلیدها رها شدهاند، پس سرعت اولیه آنها صفر در نظر گرفته میشود. افتادن کلیدها، همان سقوط آزاد است و شتاب وارد بر کلیدها، شتاب جاذبه زمین و به سمت پایین است. برای محاسبه زمان رسیدن کلیدها، کافی است از فرمول زیر استفاده کنیم:
دقت کنید جهت مثبت را به سمت بالا فرض کردهایم. پس علامت شتاب منفی باید باشد. کافی است اعداد را در فرمول بالا جاگذاری کنیم:
در آخرین مرحله جذر باید محاسبه شود که حاصل آن زمان با دو علامت میشود، اما میدانیم همیشه زمان عددی مثبت است. پس علامت منفی غیر قابل قبول است.
حرکت پرتابی
یکی دیگر از موقعیتهایی که برای بررسی آن میتوانیم از فرمول های سینماتیک استفاده کنیم، حرکت پرتابی است. حرکت پرتابی یک حرکت دو بعدی است که در آن جسم با زاویه خاصی نسبت به زمین به سمت هوا پرتاب میشود، در حالی که تنها نیروی وارد بر آن نیروی جاذبه زمین است.
چون مسیر حرکت جسم در این نوع حرکت به شکل یک سهمی است (طبق شکل زیر)، موقعیت مکانی، سرعت و شتاب جسم در هر لحظه از حرکت دارای دو مولفه افقی و عمودی است که برای نمایش این دو مولفه بهترتیب از نمادهای x و y استفاده میکنیم.
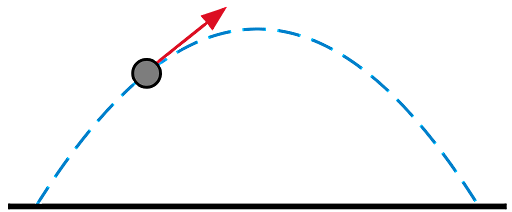
پس از مشخص کردن مولفههای حرکت در راستای دو محور x و y، میتوانیم سرعت حرکت جسم، موقعیت مکانی یا شتاب آن را در هر جهت و هر نقطه از مسیر بالا پیشبینی و تحلیل کنیم. حرکت پرتابی تمام اجسام متقارن است. اگر به شکل بالا دقت کنید، مسیر سهمی شکل حرکت پرتابی همواره نسبت به نقطهای با بیشترین ارتفاع و حداکثر برد متقارن است.
مثال ۱
اگر سنگی را طبق شکل زیر، مستقیما به سمت بالا و با سرعت اولیه پرتاب کنید، بیشترین ارتفاعی که سنگ خواهد داشت، چقدر است؟ چقدر طول میکشد تا سنگ به این ارتفاع برسد؟ شتاب جاذبه زمین را در نظر بگیرید.

پاسخ
ابتدا اطلاعاتی که در اختیار داریم را لیست میکنیم:
دو نکته در نوشتن مقادیر بالا وجود دارد. اولین نکته مربوط میشود به علامت شتاب جاذبه، که با توجه به جهتهای انتخابی برای سرعت در تصویر (سرعت با ve نشان داده شده است)، شتاب جاذبه به سمت زمین است و علامت منفی باید داشته باشد. نکته بعدی در مورد سرعت نهایی صفر است که در بالاترین ارتفاع ممکن مقدار آن خواسته شده است. در بالاترین ارتفاع ممکن، سرعت سنگ صفر میشود. چون پس از آن لحظه، سنگ تغییر مسیر داده و به سمت زمین سقوط میکند. با توجه به مقادیر بالا، بهترین فرمول جهت محاسبه حداکثر ارتفاع، فرمول مستقل از زمانی است که بر حسب y نوشته شود، چون حرکت در راستای قائم انجام شده است:
با قرار دادن مقادیر بالا و در نظر گرفتن این نکته که ارتفاع اولیه سنگ روی زمین برابر با صفر است، خواهیم داشت:
در قسمت دوم سوال، مدت زمان رسیدن به این ارتفاع خواسته شده است. با توجه به اینکه سرعتهای اولیه و نهایی را داریم و شتاب نیز مشخص است، باید از فرمولی استفاده کنیم که زمان را شامل شود. بهترین و سادهترین انتخاب، فرمول زیر است:
دقت کنید میتوانید از فرمول هم استفاده کنید. ولی این معادله بر حسب زمان از درجه دوم است و محاسبات را پیچیده میکند. بهتر است فرمولی را بکار ببریم که نیاز به محاسبات عددی کمتری داشته باشد:
اگر با فرمول درجه دو پیش بروید، باز هم همین جواب را بهدست خواهید آورد. به علت تقارن در حرکت پرتابی، مدت زمان رفتن توپ از سطح زمین تا بالاترین ارتفاع با مدت زمان برگشت توپ از بالاترین ارتفاع تا سطح زمین برابر است. همچنین میتوانیم در فرمولهای استفاده شده سرعتها را به شکل بنویسیم، اما چون میدانیم حرکت در این راستا است، از پیچیدگی بیشتر جلوگیری میکنیم
مثال ۲
فرض کنید در حالی که علی روی زمین ایستاده است، توپی را با سرعت مستقیما به سمت بالا پرتاب میکند. اگر از مقاومت هوا صرفنظر کنیم، سرعت توپ درست پیش از برخود با زمین برابر با است یا کمتر یا بیشتر از این مقدار؟
پاسخ
سرعت اولیه توپ به سمت بالا و برابر با است. اگر جهت بالا را مثبت در نظر بگیریم، قطعا در لحظه برخورد با زمین، سرعت توپ علامت منفی دارد، چون در خلاف جهت مسیر رفت است. از طرفی، در لحظهای که توپ به بالاترین نقطه مسیر خود میرسد، سرعت آن صفر است و سپس با تغییر جهت حرکت، سرعت آن منفی میشود. برای درک بهتر سوال، به شکل زیر توجه کنید:
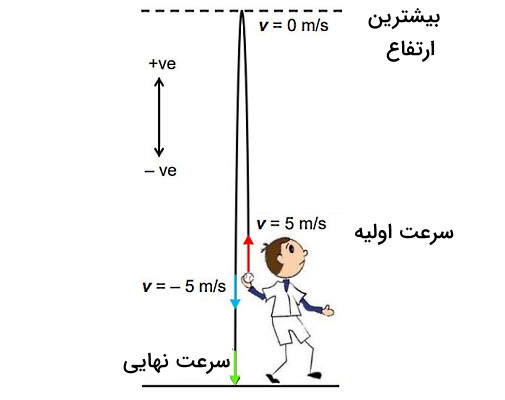
چون از مقاومت هوا صرفنظر شده است، تنها نیرویی که به توپ وارد میشود، نیروی جاذبه زمین به سمت پایین است که در تمام طول مسیر نیز تغییری نمیکند. از طرفی گفتیم مسیر حرکت یک پرتابه (جسمی که به سمت آسمان پرتاب میشود)، یک مسیر متقارن است. بنابراین سرعت توپ درست در نقطهای با ارتفاع مساوی با ارتفاع دست علی اما در جهت مخالف، برابر است با . اگر بخواهیم سرعت توپ را در لحظه برخورد با زمین پیدا کنیم، اطلاعات زیادی در اختیار نداریم. فقط میتوانیم از رابطه زیر استفاده کنیم:
فرض کنید از نقطهای معادل با ارتفاع دست علی تا زمین را در نظر داریم و برای این بخش فرمول بالا را بکار میبریم. در این صورت برابر میشود با:
همچنین برای شتاب و سرعت اولیه در این بخش از مسیر، داریم:
پس فرمول بالا به شکل زیر میشود:
اگر از این عبارت جذر بگیریم، قطعا از نظر عددی مقداری بیشتر از عدد پنج بهدست خواهد آمد. اما نکته مهم اینجا است که چون باید جهت منفی سرعت را نیز در نظر بگیریم، هنگام جذر گرفتن باید علامت منفی را برای جواب انتخاب کنیم. پس سرعت نهایی مقداری کمتر از خواهد داشت. برای مثال ممکن است برابر با یا هر عددی به این شکل شود.
سینماتیک زاویهای
پس از اینکه با کلیه فرمول های سینماتیک خطی آشنا شدیم، در این بخش کمیتها و فرمولهای سینماتیک زاویهای را بررسی میکنیم. در بخشهای ابتدایی توضیح دادیم که حرکت زاویهای چیست. متغیری که تمام کمیتهای سینماتیک زاویهای بر اساس آن ساخته میشوند، زاویه یا θ است که جهتگیری جسم را نسبت به یک محور مشخص نشان میدهد. جدول زیر نشان میدهد همتای زاویهای کمیتهای سینماتیک خطی چه هستند:
| سینماتیک خطی | سینماتیک زاویهای |
| مکان () | زاویه () |
| سرعت خطی () | سرعت زاویهای () |
| شتاب خطی () | شتاب زاویهای () |
| تکانه خطی () | تکانه زاویهای () |
فرمول های سینماتیک برای این نوع حرکت دقیقا مشابه فرمول های حرکت خطی است، فقط کافی است به جای متغیرهای خطی از متغیرهای زاویهای متناظر استفاده کنید. برای مثال فرمول سرعت زاویهای متوسط با توجه به همتای خطی خود میشود:
به همین ترتیب بقیه فرمول های سینماتیک زاویهای طبق دو جدول ابتدای نوشته بهدست میآیند. در رابطه بالا جابجایی زاویهای است و معادل است با اختلاف زاویه نهایی و زاویه اولیه جسم حول یک محور مشخص. در ادامه همراه با معرفی حرکت دایرهای میخواهیم توضیح دهیم رابطه بین حرکت خطی و زاویهای چگونه تعیین میشود.
حرکت دایره ای
شکل زیر یک حرکت دایرهای ساده را نشان میدهد که در آن جسمی در یک مسیر دایرهای شکل با شعاع در حال حرکت است. سرعت این جسم در دو لحظه روی مسیر نشان داده شده است که اندازه یکسانی برابر با دارد. اما اگر دقت کنید جهت این دو مقدار با هم یکی نیست. پس سرعت در لحظه اول با سرعت در لحظه دوم برابر نیست و حرکت جسم در این مسیر حرکت با شتاب ثابت است.

به علاوه اگر بخواهیم موقعیت جسم را در هر لحظه روی این مسیر دایرهای نشان دهیم، زاویه جسم در هر لحظه بهترین انتخاب است. اگر موقعیت جسم در لحظه اول را با زاویه و در لحظه دوم با زاویه نشان دهیم، در این صورت جابجایی زاویهای جسم برابر است با که در شکل نشان داده شده است.
حالا از اطلاعات ریاضیاتی خود در این مرحله استفاده میکنیم. میتوانیم زاویه را بر حسب کمان روبروی آن و شعاع دایره به شکل زیر بنویسیم:
از طرفی کمان روبروی این زوایه معادل است با مسافتی که جسم روی مسیر دایرهای پیموده است. میدانیم رابطه مسافت با اندازه سرعت خطی یا تندی به شکل زیر است:
با ترکیب کردن این دو رابطه خواهیم داشت:
پس با در نظر گرفتن ، به رابطه مهم زیر میرسیم که نشاندهنده رابطه بین سرعت خطی و سرعت زاویهای برای جسمی است که در یک مسیر دایرهای با شعاع در حال حرکت است:
به همین ترتیب میدانیم شتاب خطی برابر است با:
و چون شتاب زاویهای به شکل زیر تعریف میشود:
بنابراین سرعت و شتاب زاویهای با ضرب کردن مقادیر متناظر خطی در شعاع مسیر دایرهای محاسبه میشوند.
مثال
پنکهای با سرعت زاویهای شروع به چرخش میکند. چنانچه جابجایی زاویهای یکی از تیغههای آن با شتاب زاویهای برابر با باشد، سرعت زاویهای نهایی این پنکه چقدر است؟
پاسخ
برای اینکه سرعت زاویهای نهایی این چرخش را پیدا کنیم، باید ببینیم دادههای مسئله چه هستند و کدام یک از فرمول های سینماتیک اینجا مناسبتتر است. سرعت زاویهای اولیه، شتاب زاویهای و جایجایی زاویهای را داریم، در حالی که زمان چرخش داده نشده است. پس بهترین انتخاب فرمول مستقل از زمان برای سینماتیک زاویهای است:
تمرین
فرمول تبدیل معادلات مکان، سرعت و شتاب
در بخشهای قبل انواع فرمول های سینماتیک را کاملا یاد گرفتیم. در این بخش میخواهیم ببینیم اگر مکان یک جسم را بهصورت تابع یا معادلهای بر حسب زمان در اختیار داشته باشیم، چگونه و با چه فرمولی میتوانیم سرعت و شتاب این جسم را پیدا کنیم. پیشنهاد ما این است برای درک بهتر این بخش، حتما مطالعاتی در زمینه نحوه مشتقگیری یا محاسبه انتگرال یک تابع داشته باشید.
اگر مکان یک جسم را بر حسب زمان داشته باشیم، با مشتقگیری از این تابع نسبت به زمان، میتوانیم سرعت را بهدست آوریم. در مقابل، اگر سرعت بر حسب زمان را داشته باشیم، برای محاسبه معادله مکان بر حسب زمان یا تغییرات مکان با زمان کافی است از معادله سرعت نسبت به زمان انتگرال بگیریم. این روند برای تبدیلات سرعت و شتاب هم طبق دیاگرام بالا برقرار است. پس اگر مکان یا جابجایی ما به شکل باشد، در این صورت سرعت و شتاب برابر خواهند شد با:
مثال ۱
اگر جابجایی ذرهای نسبت به مکان با تابع زیر نمایش داده شود، ابتدا معادله شتاب را بهدست آورید و سپس تعیین کنید شتاب ذره در لحظه چقدر است؟
پاسخ
ابتدا با مشتقگیری از تابع بالا نسبت به زمان، معادله سرعت را پیدا میکنیم و سپس با مشتقگیری از سرعت، معادله شتاب بهدست خواهد آمد:
میدانیم اگر تابعی بر حسب زمان بهصورت باشد، مشتق آن نسبت به زمان برابر است با . برای پاسخ دادن به بخش دوم سوال، کافی است زمان داده شده را در معادله شتاب قرار دهیم تا شتاب در این لحظه محاسبه شود. در حقیقت معادله شتاب را به شکل داریم. پس باید را حساب کنیم:
مثال ۲
اگر موقعیت مکانی جسمی با معادله زیر توصیف شود، معادلات سرعت و شتاب زاویهای آن کدام است؟
پاسخ
در این سوال موقعیت جسم بر اساس زاویه بیان شده و به همین علت بهجای مکان، زاویه بر حسب زمان داده شده است. پس با سینماتیک زاویهای مواجه هستیم. معادلات دقیقا مانند معادلات خطی است:
مسیر یادگیری سینماتیک دانشگاهی با فرادرس
یکی از مهمترین مباحث فیزیک دانشگاهی اغلب رشتههای مهندسی و علوم پایه، مکانیک و آشنایی با فرمول های سینماتیک است. به همین دلیل در این بخش قصد داریم چند فیلم آموزشی مرتبط با این موضوع را به شما معرفی کنیم. مشاهده این دورههای فرادرس به شما کمک میکند تا با حل مثالها و تمرینهای متنوعتر در قالب صدا و تصویر درک بسیار عمیقتری نسبت به این مبحث کسب کنید:
- فیلم آموزش رایگان بردارها در فیزیک ۱ دانشگاهی
- فیلم آموزش فیزیک پایه ۱
- فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله
- فیلم آموزش فیزیک پایه ۱ مرور و حل مساله
- فیلم آموزش فیزیک پایه ۱ مرور و حل تست
آزمون سینماتیک
در آخرین بخش از این مطلب مجله فرادرس، آزمونی متشکل از ده سوال چهار گزینهای را برای شما تهیه کردهایم تا با پاسخدهی به این سوالات، مهارت خود را در استفاده از فرمول های سینماتیک بیازمایید. در انتهای آزمون، با کلیک روی بخش «دریافت نتیجه آزمون» میتوانید نمره نهایی خود را مشاهده کنید.












