فرمول رادیکال در اکسل — از صفر تا صد

رادیکال یا ریشه اعداد، یک عملگر ریاضی است که می‌توان آن را معکوس توان‌رسانی در نظر گرفت. متاسفانه محاسبه رادیکال برای اعداد احتیاج به اجرای روال پیچیده و طولانی دارد. بنابراین در بیشتر نرم‌افزارهای محاسباتی مانند اکسل، تابعی برای محاسبه آن وجود دارد. به همین دلیل در این نوشتار از مجله فرادرس به بررسی نحوه اجرای فرمول رادیکال در اکسل خواهیم پرداخت. البته علاوه بر استفاده از تابع، می‌توانیم عمل توان‌رسانی را به شکلی در اکسل انجام دهیم که ریشه‌گیری به صورت توان رساندن اجرا شود. پس با ما همراه باشید تا بوسیله روابط و محاسبه فرمول رادیکال در اکسل را فراگیرید.

برای آشنایی بیشتر با موضوع ریشه‌گیری پیشنهاد می‌شود مطالب دیگر مجله فرادرس مانند اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده و جذر یا محاسبه ریشه دوم عدد — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتار معادله رادیکالی — به زبان ساده و فرمول نویسی در اکسل — به زبان ساده نیز خالی از لطف نیست.

فرمول رادیکال در اکسل

حتما با نحوه محاسبه رادیکال آشنایی دارید. البته برای محاسبه ریشه یا جذر که با نماد رادیکال (√) نمایش داده می‌شود، به صورت تقریبی، تکنیک‌های هندسی وجود دارد. که البته طولانی و با اجرای مراحل تکراری صورت می‌گیرند. همچنین اعدادی که برای گرفتن ریشه یا رادیکال انتخاب کرده‌اید، صحیح باشند، روش‌های هندسی و تقریبی برای مشخص کردن مقدار آن‌ها وجود دارد.

فیلم آموزش استفاده از توابع و فرمول نویسی در اکسل Excel در فرادرس

کلیک کنید

در این نوشتار به کمک اکسل می‌خواهیم جذر یا ریشه اعداد را محاسبه کنیم. این کار را به کمک دو تکنیک در اکسل انجام می‌دهیم. ابتدا با استفاده از فرمول نویسی محاسبه فرمول رادیکال در اکسل را اجرا می‌کنیم. سپس با استفاده از توابع موجود در اکسل که در بخشی توابع ریاضی قرار دارند، ریشه اعداد را بدست می‌آوریم. در این بین با ذکر مثال‌هایی، موضوع را برای فراگیران روشن‌تر خواهیم کرد. ابتدا بهتر است که در مورد محاسبه ریشه یا رادیکال بیشتر بدانیم.

می‌دانیم که رادیکال، یک عمل ریاضی است که به دو پارامتر به کار می‌رود. ابتدا باید عددی که قرار است رادیکال برایش محاسبه شود را مشخص کرده، سپس فرجه رادیکال با مرتبه ریشه‌گیری را تعیین کنیم. به رابطه زیر دقت کنید.

$$\large \sqrt[ n]{ a}$$

رابطه ۱

در اینجا $$n$$ را فرجه رادیکال و $$a$$ را عدد زیر رادیکال می‌نامند. این امر به این معنی است که قرار است ریشه $$n$$ام عدد $$a$$ را بدست آوریم. به این ترتیب اگر ریشه سوم عدد ۱۹ مورد نظر باشد، مقدار ۳، فرجه و ۱۹ عدد رادیکال گیری است. این عبارت را به صورت زیر نمایش می‌دهیم.

$$\large \sqrt[ 3]{ 19}= 2.6684$$

شیوه دیگری نیز برای نمایش این مقدار وجود دارد. می‌توان از عبارت‌های توانی برای مشخص کرده ریشه کمک گرفت. معادل رابطه ۱ برای نمایش ریشه به صورت زیر است.

$$\large {a}^{ \frac{ 1}{ n}}$$

رابطه ۲

واضح است که منظور از توان کسری، همان معکوس مقدار فرجه رادیکال است. برای مثال ریشه سوم عدد ۱۹ به شکل توان‌دار خواهیم نوشت. با توجه به تعریفی که برای ریشه‌گیری یا رادیکال و ارتباط آن با توان‌رسانی داریم، می‌دانیم رابطه زیر معادل با رابطه بالا است.

$$\large 19^{ \frac{ 1}{ 3}} = 2.6684$$

همانطور که دیدید، می‌توان فرجه رادیکال را همان معکوس مقدار توان در نظر گرفت. از آنجایی که فرجه رادیکال ۳ بود، اگر ۱۹ را به توان معکوس ۳ یعنی ۱/۳ برسانیم، نتیجه یکسانی خواهیم گرفت.

حتی این امکان وجود دارد که فرجه عدد صحیح نباشد. البته در این حالت اغلب نمایش رادیکالی را به صورت عدد توان‌دار انجام می‌دهند. برای مثال به جای آنکه ریشه ۱٫۲۵ را به کار ببرند از حالت توانی ولی به صورت معکوس ۱٫۲۵ استفاده می‌کنند.

$$\large \sqrt[ 1. 25]{ 19} = 19^{ \frac{ 1}{ 1.25} } = 19^{ \frac{ 1}{ \frac{ 125}{ 100}}} = 19^{ \frac{ 100}{ 125}} = 19^{ \frac{ 4}{ 5}} = 10.544$$

نکته دیگری که در اینجا قابل استفاده است، نمایش ریشه‌های اعداد توان‌دار است. برای مثال فرض کنید که می‌خواهیم ریشه $$n$$ام عدد $$a^b$$ را بدست آوریم. رابطه شماره ۳ در اینجا به کارمان می‌آید.

$$\large \sqrt[n]{a ^b} = a^{ \frac{ b}{ n} }$$

رابطه ۳

بنابراین ریشه سوم عدد ۱۹ به توان ۲ به شکل زیر بدست می‌آید.

$$\large \sqrt[ 3]{ 19^2} = 19^{ \frac{ 2}{ 3}}$$

البته در اینجا نمی‌خواهیم این محاسبه را انجام دهیم. در ادامه فرمول رادیکال در اکسل را مورد استفاده قرار داده و نتیجه را بدست خواهیم آورد.

فرمول رادیکال در اکسل

همانطور که گفتیم، محاسبه یا فرمول رادیکال در اکسل را می‌توان به صورت یک عبارت توان‌دار محاسبه کرد. باز هم فرض کنید که قرار است ریشه سوم عدد ۱۹ را بدست آوریم. به این منظور ابتدا یک کاربرگ خالی اکسل ایجاد کرده، مقدار ۱۹ را در سلول A1 وارد می‌کنیم. واضح است که این سلول همان نقش $$a$$ را در رابطه ۱ یا ۲ دارد. همچنین مقدار فرجه در رابطه ۱ (یعنی همان $$n$$) را در سلول B1 می‌نویسیم. پس مقدار B1 برابر با ۳ است. فرض کنید قرار است نتیجه ریشه سوم عدد ۱۹ را در سلول C1 مشاهده کنیم. بنابراین فرمول را در این سلول به شکل زیر وارد خواهیم کرد.

C1 : =A1 ^(1 / B1)

توجه دارید که پرانتز را به این علت استفاده کرده‌ایم که عمل توان یعنی (^) نسبت به تقسیم اولویت دارد و اگر پرانتز وجود نداشت، ابتدا A1 به توان ۱ می‌رسید، سپس بر B1 تقسیم می‌شد که نظر ما را از عملیات ریاضی برآورده نمی‌کرد. در کاربرگی که در تصویر ۱ دیده می‌شود این عملیات اجرا شده است.

فیلم آموزش اکسل – محاسبات ریاضی و ماتریسی با Microsoft Excel 2016 در فرادرس

کلیک کنید

نکته: اولویت‌های محاسباتی برای عملگرهای ریاضی در اکسل از ضعیف به قوی به صورت، جمع-تفریق، سپس ضرب-تقسیم آنگاه توان و در انتها پرانتز است. بنابراین عملیات داخل پرانتز بالاترین اولویت را دارند و در یک فرمول اول از همه محاسبه می‌شوند.

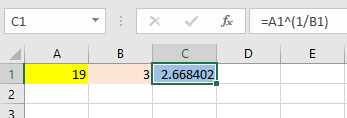
در این تصویر مشخص است که ریشه سوم ۱۹ برابر است با ۲٫۶۶۸۴. همچنین توجه داشته باشید که پارامتر این تابع با آدرس A1 مشخص شده که مقدار ۱۹ در آن ثبت شده. البته می‌توانستیم فرمول را به صورت غیر پارامتری نیز بنویسیم و با ایجاد یک سلول مستقل، محاسبات را انجام می‌دادیم. به فرمول زیر دقت کنید.

C2: = 19^(1/3)

با این کار اگر لازم باشد که ریشه دیگری از عدد ۱۹ محاسبه شود، مجبور به تغییر مقدار درون فرمول بودیم. حتی اگر مقدار ۱۹ نیز باید تغییر می‌یافت، چاره‌ای جز جایگزین کردن مقدار ۱۹ با عدد دیگر درون فرمول وجود نداشت. در حالیکه روش قبلی که فرمول به صورت وابسته نوشته شده بود، این اجازه را به ما می‌داد که با تغییر مقدار A1 یا B1، مقدار زیر ردیکال یا فرجه رادیکال را تغییر دهیم.

تابع رادیکال در اکسل

همانطور که گفتیم، دو روش برای اجرای فرمول رادیکال در اکسل وجود دارد. تابع SQRT برای محاسبه ریشه دوم عدد به کار می‌رود. می‌دانید که باید حتما برای ریشه‌های زوج، مقدار زیر رادیکال، مثبت باشد. بنابراین پارامتر تابع SQRT فقط مقادیر مثبت را می‌پذیرد. شکل دستوری این تابع به صورت زیر است.

SQRT(number)

تنها پارامتر این تابع همان number یعنی مقدار زیر رادیکال است. برای مثال اگر بخواهیم ریشه دوم عدد ۱۹ را محاسبه کنیم، در سلولی (مثلا D1) تابع را به صورت زیر به کار می‌بریم.

D1: =SQRT(A1)

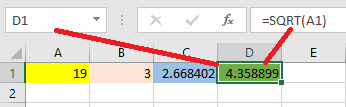
نکته: معرفی و به کار بردن نام تابع در اکسل به حروف بزرگ و کوچک حساس نیست. در نتیجه اگر این تابع را به شکل sqrt نیز بنویسید مشکلی بوجود نخواهد آمد.

این بار مقدار A1 را به ۱۹- تغییر می‌دهیم. مشخص است که برای مقادیر منفی، ریشه زوج (مثلا در اینجا ۲) وجود ندارد. اکسل با پیغام خطای !NUM# نشان می‌دهد که امکان محاسبه چنین تابعی وجود ندارد. تصویر ۲، به نمایش کاربرگی اختصاص دارد که برای محاسبه ریشه دوم اعداد تنظیم شده.

اگر بخواهید ریشه‌های دوم اعداد توان‌دار را محاسبه کنید، می‌توانیم در پارامتر تابع SQRT تغییراتی بوجود آوریم. برای مثال اگر قرار است ریشه دوم عدد $$4^3$$ را بدست آوریم، کافی است که مقدار $$4^3$$ را به عنوان پارامتر معرفی کنیم. پس در یک سلول اکسل خواهیم نوشت:

= sqrt(3^4)

بنابراین برای محاسبه ریشه‌های زوج از این روش استفاده خواهیم کرد. مشخص است که رابطه ۳ در این میان نقش مهمی ایفا می‌کند. برای مثال ریشه چهارم عدد ۲ را به کمک تابع SQRT و با تکنیک گفته شده، بدست می‌آوریم. به فرمول زیر و تعداد پرانتزها و محل قراگیری آن‌ها دقت کنید.

= sqrt( 2^ (1/2) ) 

نتیجه برابر است با 1٫189207115 که البته با رابطه زیر یکسان است.

= 2^(1/4)

حتی می‌توانیم از تابع SQRT برای پیدا کردن ریشه‌های مختلف هر عددی هم استفاده کنیم. کافی است فرجه رادیکال را به صورت مضربی از دو درآوریم. فرض کنید قرار است ریشه سوم عدد ۱۹ را محاسبه کنیم. فرمول یا تابع SQRT را به صورت زیر به کار می‌بریم. واضح است که نتیجه همان مقدار:

= SQRT (19^(2/3))

توابع خاص فرمول رادیکال در اکسل برای اعداد

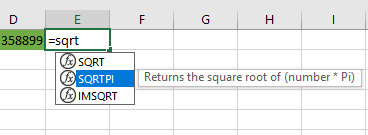
توجه داشته باشید که دو تابع دیگر نیز در اکسل وجود دارند که ریشه دوم را محاسبه می‌کنند. اولی تابع SQRTPI است که ریشه دوم حاصل‌ضرب یک عدد در عدد پی ($$\pi$$) را محاسبه می‌کند و تابع دوم هم IMSQRT است که ریشه دوم اعداد مختلط را بدست می‌آورد. دسترسی به این دو تابع در تصویر ۳ دیده می‌شوند.

فیلم آموزش اکسل Microsoft Excel 2019 – مقدماتی در فرادرس

کلیک کنید

در تابع اول یعنی SQRTPI یک پارامتر وجود دارد که همان عددی است که به عنوان مضرب پی مشخص شده. برای مثال تابع زیر، ریشه دوم عدد پی را مشخص می‌کند.

= SQRTPI(1)

و اگر به رادیکال یک و نیم برابر عدد پی احتیاج داشته باشید، از فرمول زیر کمک بگیرید. به یاد داشته باشید که این مضرب همیشه باید مقداری مثبت باشد، زیرا ریشه‌های زوج برای مقادیر منفی تعریف نشده است. به این ترتیب ریشه اعداد مرکبی که به صورت مضارب عدد پی هستند، محاسبه می‌شود.

= SQRTPI(1.5)

تابع دوم یعنی IMSQRT که در گروه توابع ریاضی قرار دارد، برای محاسبه ریشه دوم عدد مختلط مناسب است. به منظور ورود پارامتر این تابع، باید عدد مختلط را به صورت یک عبارت متن و به صورت زیر معرفی کنید.

x + y i

واضح است که x بخش حقیقی و y بخش موهومی است. همانطور که می‌دانید، i نیز همان مقدار یکه مختلط است که ریشه دوم عدد ۱- را مشخص می‌کند. در این حالت تابع IMSQRT به صورت زیر محاسبه می‌شود.

$$\large \sqrt{ x + yi } = \sqrt{ r} \cos \left( \dfrac{ \theta}{ 2} \right) + i \; \sqrt{r} \sin \left( \dfrac{ \theta}{ 2}\right)$$

که در آن $$r$$ و $$\theta$$ براساس روابط زیر حاصل می‌شوند.

$$\large r = \sqrt{ x^2 + y^2 }$$

$$\large \theta = \tan^{ -1} \left( \dfrac{y }{x} \right) , \;\;\; \theta \in \left( -\pi , \pi \right]$$

بنابراین اگر فرمول به صورت زیر بنویسیم، ریشه دوم عدد 1 + i را بدست آورده‌ایم. به علامت " " که عبارت یا عدد مختلط در آن نوشته شده، دقت کنید.

=IMSQRT("1+i")

مقدار این ریشه، به صورت نمایش داده می‌شود که خود، یک عدد مختلط است.

1.09868411346781+0.455089860562227i

نکته: پیشوند IM در نام این تابع، نشان‌دهنده Imaginary یا همان موهومی است که به تابع SQRT اضافه شده.

به یاد داشته باشید که حتما باید عدد مختلط را به عنوان پارامتر به صورت متنی وارد کنید. این به معنی آن است که عدد مختلط را داخل دو علامت گیومه ("") قرار دهید و سپس فرمول رادیکال در اکسل را به کار گیرید.

خلاصه و جمع‌بندی

همانطور که در این مطلب خواندید، به دو روش برای محاسبه فرمول رادیکال در اکسل اقدام کردیم. در روش اول با استفاده از تابع SQRT، ریشه دوم را بدست آوردیم و در روش دوم با استفاده از تکنیک توان رساندن ریشه n ام یک عدد را محاسبه کردیم. به یاد داشته باشید که ریشه دوم یا ریشه‌های زوج فقط برای مقادیر مثبت قابل محاسبه هستند و اگر این مقدار منفی باشد، اکسل با خطایی اطلاع می‌دهد که امکان نمایش نتیجه وجود ندارد. ریشه های فرد برای اعداد منفی قابل محاسبه است و مشکلی از این نظر وجود ندارد.

هر چند اکسل ابزار محاسباتی برای عملیات ریاضی است ولی هنگام به کار بردن توابع و فرمول‌های آن، باید نکاتی که در این متن به آن اشاره شد را هم در نظر بگیرید تا اولویت های عملگرها به شکل درست به کار رفته و نتیجه حاصل دقیق و مطابق با نظر شما صورت گیرد. به این منظور آموزشی نیز در این مطلب معرفی شد که مشاهده آن برای فراگیری اکسل بخصوص برای اجرای فرمول و توابع ریاضی مفید است.