شعاع ژیراسیون و محاسبه آن — از صفر تا صد
در مطلب لختی دورانی و «ممان اینرسی» (Moment of Inertia)، توضیح دادیم که قانون دوم نیوتن و لختی دورانی چگونه با هم در ارتباط هستند. جالب است بدانید که برای یک جسم دورانکننده، میتوان شعاعی در نظر گرفت که به نظر برسد کل جرم جسم در یک نقطه متمرکز شده و در فاصلهای برابر با این شعاع نسبت به محور، در حال دوران است. این شعاع تحت عنوان شعاع ژیراسیون (Radius of Gyration) شناخته میشود.
شعاع ژیراسیون
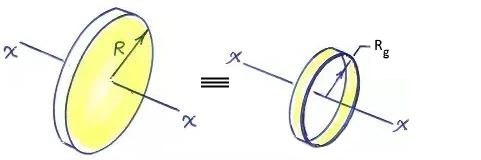
شعاع ژیراسیونِ یک جسم () ، فاصلهای است که اگر کل جرم جسم را در حلقهای یکنواخت با این شعاع توزیع کنیم، در این صورت لختی دورانی آن برابر با لختی دورانی جسمِ اولیه است. در شکل زیر این مفهوم نشان داده شده است.
جسمی را در نظر بگیرید که از چندین جرم متمرکز شده به اندازه که در فواصل قرار گرفتهاند، تشکیل شده است. در این صورت میتوان لختی دورانی ایجاد شده در نتیجه هریک از اجرام را محاسبه کرده و با میانگینگیری از آنها، لختی دورانی را بدست آورد. برای چنین جسمی، لختی دورانی برابر است با:
حال حالتی را در نظر بگیرید که در آن تمامی جرمها برابر باشند. در این صورت لختی دورانی را میتوان به صورت زیر بازنویسی کرد.
با فرض اینکه رابطه نشاندهنده جرم کل جسم باشد، در این صورت میتوان رابطه لختی دورانی را به صورت بازنویسی کرد.
با توجه به تعریف شعاع ژیراسیون، میتوان لختی بدست آمده در بالا را برابر با لختی ناشی از شعاع ژیراسیون در نظر گرفت. با استفاده از این معادلسازی داریم:
در نتیجه شعاع ژیراسیون مطابق با رابطه زیر بدست خواهد آمد.
بنابراین میتوان گفت شعاع ژیراسیون یک جسم متناسب با توان دوم فواصلی است که جرمها از آن قرار گرفتهاند.
مثال ۱
مطابق با شکل زیر دیسکی به شعاع را در نظر بگیرید که میخواهیم شعاع ژیراسیون آن را بدست آوریم.
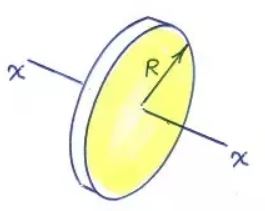
در ابتدا لختی دورانی دیسک فوق را مطابق با رابطه زیر بدست میآوریم:
در مرحله بعد مطابق با شکل زیر فرض میکنیم که کل جرمِ دیسک در فاصله از محور دوران قرار گرفته است.
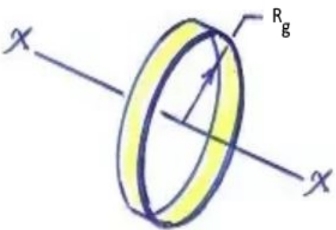
کاربردها در مهندسی سازه
در مهندسی سازه، از شعاع ژیراسیون به منظور توصیف نحوه توزیع جرمِ یک مقطع از ستون حول محور دورانش استفاده میشود. در این حالت از رابطه زیر جهت بدست آوردن شعاع ژیراسیون استفاده میشود.
در رابطه فوق، نشاندهنده لختی دورانی و ، شعاع ژیراسیون را نشان میدهد. در این موارد از مفهوم ژیراسیون برای تخمین زدن اندازه سختی ستون نیز استفاده میشود. اگر گشتاورهای دورانی تانسور ژیراسیون حول دو محور برابر نباشند، در این صورت تیر حول محوری خم خواهد شد که گشتاور دورانی حول آن کمتر باشد. برای نمونه تیری با مقطعی بیضی شکل، حول محور کوتاهترش خم خواهد شد.
در مهندسی معمولا با اجسامی سر و کار داریم که در آنها توزیع جرم به صورت پیوسته است. بنابراین در چنین مواردی میتوان با استفاده از انتگرال، شعاع ژیراسیون را بدست آورد.
کاربردها در مکانیک و فیزیک
در مکانیک معمولا از شعاع ژیراسیون به منظور تحلیل حرکت اجسام پیچیده استفاده میشود. در چنین اجسامی میزان شتاب زاویهای یا خطی جسم وابسته به لختی دورانی جسم حول محورهای مختلف است. از این رو از شعاع ژیراسیون به منظور تحلیل حرکت جسم در حالتی استفاده کرد که در آن توزیع جرمی جسم به صورت یکنواخت در نظر گرفته میشود.
در این موارد نیز از یکی از روابط زیر بهمنظور بدست آوردن لختی دورانی استفاده میشود.
توجه داشته باشید که در رابطه فوق، اسکالر بوده و برابر با تانسور گشتاور اینرسی نیست. جالب است بدانید که شعاع ژیراسیون دارای کاربردهایی مولکولی نیز است. در حقیقت در فیزیک پلیمری از شعاع ژیراسیون به منظور توصیف ابعاد زنجیره پلیمری استفاده میشود. برای نمونه شعاع زنجیره پلیمری یک مولکول در لحظهای مشخص برابر است با:
در عبارت فوق، ، نشاندهنده فاصله میانگین مونومرها است. همانطور که در ادامه نیز نشان داده شده، شعاع ژیراسیون وابسته به توان دوم فاصله مونومرها از یکدیگر نیز است.
البته به عنوان روشی جایگزین میتوان با جمع زدن گشتاورهای اصلی تانسور ژیراسیون نیز شعاع ژیراسیون را بدست آورد. البته در آینده در مورد نحوه استفاده از شعاع ژیراسیون در شاخههای مختلف بحث خواهیم کرد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^












