تقسیم عبارت های جبری — به زبان ساده + حل تمرین و مثال

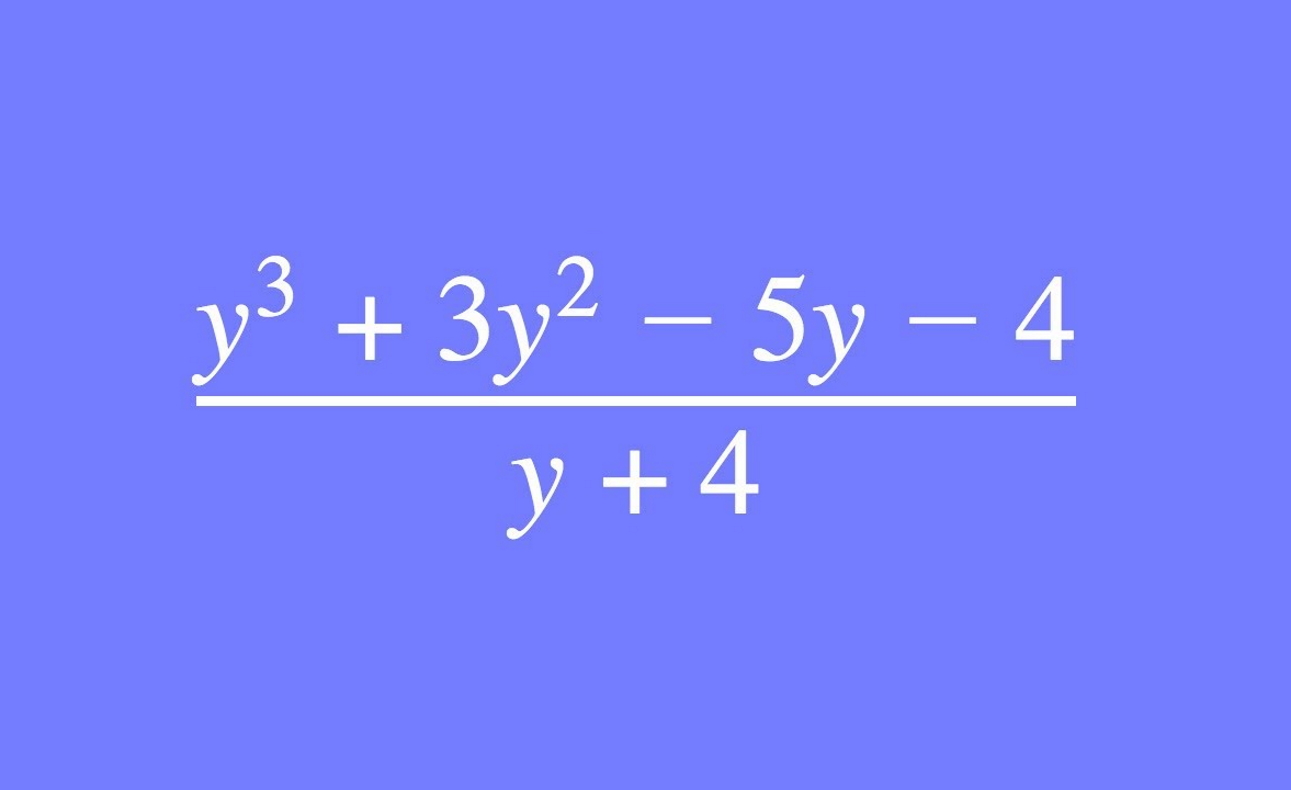
در آموزش‌های پیشین مجله فرادرس، با ضرب عبارت‌های جبری آشنا شدیم. همچنین، مطالبی را درباره تجزیه و ساده کردن این عبارت‌ها بیان کردیم. در این آموزش، به تقسیم عبارت های جبری می‌پردازیم و مثال‌هایی از آن را حل می‌کنیم.

عبارت های جبری

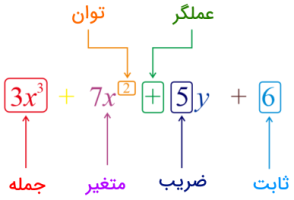
عبارت‌های جبری ترکیبی از متغیرها و ثابت‌ها هستند که توسط چهار عمل اساسی حسابیِ جمع، تفریق، ضرب و تقسیم به هم متصل می‌شوند. شکل زیر یک عبارت جبری را نشان می‌دهد که بخش‌های مختلف آن مشخص شده‌اند.

• ثابت: به نمادی که مقدار عددی ثابتی دارد، ثابت می‌گویند. برای مثال، اعداد $$ 5 $$ و $$ - 6 $$ و $$ 142$$ و... ثابت هستند.
• متغیر: نمادی است که مقدارهای عددی مختلفی را به خود می‌گیرد. برای مثال، در عبارت جبری $$ 3 x + 5 $$، جمله $$ 5 $$ ثابت و $$ x $$ متغیر است.
• جمله: بخش‌های مختلف یک عبارت جبری که با «+» یا «−» از هم جدا شده‌اند، جمله‌های عبارت نامیده می‌شوند. برای مثال، $$ 3x + 2 y$$ یک عبارت جبری است که از دو جمله تشکیل شده است.
• ضریب: در یک جمله عبارت جبری، ضریب معمولاً عددی است که در جمله ضرب می‌شود. برای مثال در عبارت $$ 2 x y ^ 2 $$ ضریب عدد $$2$$ است. البته ضریب را به‌صورت حاصل‌ضرب عدد و متغیر نیز در نظر می‌گیرند. برای مثال، در جمله $$ 3 x y $$، ضریب $$ y $$ عبارت $$ 3 x $$ است، همچنین، ضریب $$ x $$ عبارت $$ 3 y $$ است، همچنین ضریب $$ x y $$ عدد $$ 3 $$ است.
• عامل: اگر بتوان یک عبارت جبری را به‌صورت حاصل‌ضرب عبارت‌های جبری نوشت، به هر یک از این عبارات، عوامل عبارت جبری گفته می‌شود. برای مثال، در عبارت جبری $$ 4 x ^ 2 + 2 x $$، عامل‌ها $$ 2 x $$ و $$ (2x+1)$$ هستند، زیرا $$ 4 x ^ 2 + 2 x = 2 x (2x + 1 )$$.
• جملات متشابه و غیرمتشابه: جملات دارای عوامل جبری یکسان به‌عنوان جملات متشابه شناخته می‌شوند. در غیر این صورت، آن‌ها را جملات غیرمتشابه می‌نامیم. برای مثال، در عبارت $$ 2 a^{2} b-7 a b-4 b a^{2}$$، جملات $$ 2 a^{2} b$$ و $$-4 b a^{2}$$ متشابع هستند، اما جمله $$-7 a b$$ غیرمتشابه است.

انواع عبارت‌های جبری

بر اساس تعداد جملات می‌توان عبارات جبری را به انواع تک‌جمله‌ای، دوجمله‌ای، سه‌جمله‌ای و... طبقه‌بندی کرد.

• یک‌جمله‌ای: یک عبارت جبری که فقط یک جمله داشته باشد، یک‌جمله‌ای یا تک‌جمله‌ای نامیده می‌شود. برای مثال، $$ 5 $$ و $$ 2 x $$ و $$ 3a ^ 2 $$ و $$4xy$$ تک‌جمله‌ای هستند.
• دو‌جمله‌ای: به عبارت جبری‌ای که دارای دو جمله است که با علامت جمع (+) یا علامت تفریق (-) از هم جدا شده‌اند، دوجمله‌ای می‌گویند. عبارت‌های $$2 x+3$$ و $$3 x-1$$ و $$2 x+5 y$$ و $$6 x-3 y$$ نمونه‌هایی از دوجمله‌ای هستند.
• سه‌جمله‌ای: عبارت جبری‌ای که دقیقاً سه جمله داشته باشد، سه‌جمله‌ای نامیده می‌شود. عبارت‌های $$4 x^{2}+9 x+7$$ و $$12 p q+4 x^{2}-10$$ و $$3 x+5 x^{2}-6 x^{3}$$ نمونه‌هایی از سه‌جمله‌ای‌ها هستند.
• چهارجمله‌ای: به عبارت جبری‌ای که دقیقاً چهار جمله داشته باشد، چهارجمله‌ای می‌گویند. برای مثال، $$4 x^{2}+3 x^{3}+9 x+7$$ و $$12 p q+4 s+4 x^{2}-10$$ و $$3 x^{4}+3 x+5 x^{2}-6 x^{3}$$ چهارجمله‌ای هستند.
• چند‌جمله‌ای: عبارات جبری‌ای که دارای یک یا چند جمله باشد، چندجمله‌ای نامیده می‌شوند.

تقسیم عبارت های جبری

در جبر، می‌توانیم تقسیم عبارت های جبری را به سه دسته تقسیم کنیم:

1. تقسیم یک تک‌جمله‌ای به تک‌جمله‌ای دیگر
2. تقسیم یک چندجمله‌ای به یک تک‌جمله‌ای
3. تقسیم یک چندجمله‌ای به چندجمله‌ای دیگر

در بخش‌های بعدی، به روش انجام تقسیم عبارت های جبری می‌پردازیم. فرمول اصلی الگوریتم تقسیم عبارت های جبری همان چیزی است که برای تقسیم اعداد داریم و با آن آشنا هستیم:

باقیمانده + (خارج قسمت × مقسم‌علیه) = مقسوم

برای مثال، در تساوی زیر، عدد ۱۰۵ مقسوم است، عدد ۸ مقسوم علیه، عدد ۱۳ خارج قسمت و عدد ۱ باقیمانده:

$$ \large 105 = 8 \times 13 + 1 $$

برای آشنایی بیشتر با این موضوع، پیشنهاد می کنیم به آموزش «مقسوم ، مقسوم علیه و باقیمانده چیست؟ — به زبان ساده» مراجعه کنید.

تقسیم تک جمله ای به تک جمله ای

هنگام تقسیم یک تک‌جمله‌ای بر یک تک‌جمله‌ای دیگر، دو قانون وجود دارد که باید در نظر داشته باشیم:

قانون 1: ضریب خارج قسمت دو تک‌جمله‌ای برابر با خارج قسمت ضرایب آن‌هاست.

قانون 2: متغیر خارج قسمت دو تک‌جمله‌ای، برابر با خارج قسمت متغیرهای آن‌هاست.

برای مثال، حاصل تقسیم $$ 12 x^{3} y^{2} $$ بر $$3 x^{2} y $$ به‌شکل زیر محاسبه می‌شود:

$$ \large \frac { 1 2 x ^ { 3 } y ^ { 2 } } { 3 x ^ { 2 } y } = \frac { 1 2 \times x \times x \times x \times y \times y } { 3 \times x \times x \times y } = 4 \times x \times y = 4 x y $$

تقسیم چند جمله ای به تک جمله ای

تقسیم چندجمله‌ای به تک‌جمله‌ای می‌توانیم از دو روش استفاده کنیم:

۱. هریک از جملات چندجمله‌ای داده‌شده را تک به تک بر تک‌جمله ای تقسیم کنیم. این روش، روش حذفی (Cancellation) نامیده می‌شود.

۲. در صورت امکان، می‌توانیم از چندجمله‌ای فاکتور بگیریم و اگر اگر این فاکتورها مشابه تک‌جمله‌ای باشند، آن‌ها را با هم ساده کنیم. این روش را روش عامل مشترک می‌نامند.

اکنون مثالی را بررسی می‌کنیم که در آن از هر دو روش استفاده می‌شود.

می‌خواهیم چندجمله‌ای $$ x ^ {3 } y ^ { 3 } + x ^ { 2 } y ^ { 3 } - x y ^ { 4 } + x y $$ را بر تک‌جمله‌ای $$x y $$ تقسیم کنیم.

ابتدا از روش اول تقسیم را انجام می‌دهیم. بدین منظور، تک‌تک جملات چندجمله‌ای را بر تک‌جمله‌ای تقسیم می‌کنیم:

$$ \large \begin {align} \frac { x ^ { 3 } y ^ { 3 } + x ^ { 2 } y ^ { 3 } - x y ^ { 4 } + x y } { x y } & = \frac { x ^ { 3 } y ^ { 3 } } { x y } + \frac { x ^ { 2 } y ^ { 3 } } { x y } - \frac { x y ^ { 4 } } { x y } + \frac { x y } { x y } \\
& = x ^ { 2 } y ^ { 2 } + x y ^ { 2 } - y ^ { 3 } + 1 \end {align} $$

اکنون با روش عامل مشترک حاصل تقسیم را به‌دست می‌آوریم. بدین منظور، باید از جمله متشابه تک‌جمله‌ای فاکتور بگیریم:‌

$$ \large \begin {align}
& x ^ { 3 } y ^ { 3 } + x ^ { 2 } y ^ { 3} - x y ^ { 4 } +x y \\
& = x \times x \times x \times y \times y \times y+x \times x \times y \times y \times y-x \times y \times y \times y \times y + x \times y
\\ & = x y ( x \times x \times y \times y + x \times y \times y - y \times y \times y + 1 )
\end {align} $$

در نتیجه، خواهیم داشت:‌

$$ \large \begin {align}
& x ^ { 3 } y ^ { 3 } + x ^ { 2 } y ^ { 3 } - x y ^ { 4 } + x y \div x y \\ & = \frac { x y ( x \times x \times y \times y + x \times y \times y - y \times y \times y + 1 ) } { x y } \\ &
= x ^ { 2 } \times y ^ { 2 } + x \times y ^ { 2 } - y ^ { 3 } + 1 \\& = x ^ { 2 } y ^ { 2 } + x y ^ { 2 } - y ^ { 3 } + 1
\end {align} $$

تقسیم چند جمله ای بر چند جمله ای

روش تقسیم یک چندجمله‌ای به چندجمله‌ای دیگر با درجه یکسان یا پایین‌تر با نام «تقسیم طولانی عبارت‌های جبری» شناخته می‌شود. در روش تقسیم طولانی چندجمله‌ای، صورت و مخرج هر دو چند‌جمله‌ای هستند. این موضوع در شکل زیر نشان داده شده است.

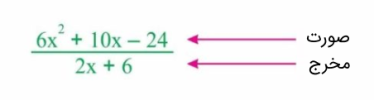
تقسیم طولانی چندجمله‌ای‌ها از مقسوم، مقسوم‌علیه، خارج قسمت و باقیمانده تشکیل شده است.

شکل زیر این چهار مورد را نشان می‌دهد.

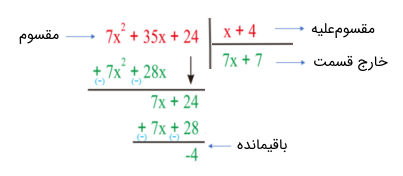
مراحل تقسیم طولانی عبارت های جبری

روش تقسیم طولانی عبارت‌های جبری به‌شرح زیر است:

مرحله 1: چندجمله‌ای‌ها را از بزرگ‌ترین درجه به کوچک‌ترین درجه (به‌ترتیب نزولی) مرتب کنید. اگر عبارتی وجود ندارد، در آن مکان $$0$$ قرار دهید. برای مثال، می‌خواهیم با استفاده از روش تقسیم طولانی، چند‌جمله‌ای $$ a ( x ) = 6 x ^ { 4 } + 3 x - 9 x ^ { 2 } + 6 $$ را بر چندجمله‌ای درجه دوم $$ b ( x ) = x ^ { 2 } - 2 $$ تقسیم کنیم.

ابتدا چندجمله‌ای داده‌شده را به‌ترتیب نزولی درجه آن مرتب می‌کنیم.

مرحله ۲: عدد $$0$$ را به‌عنوان ضریب عبارت‌هایی که وجود ندارند، قرار می‌دهیم. دو چندجمله‌ای به‌شکل زیر هستند:

$$ \large \begin {align}
a ( x ) & : 6 x ^ { 4 } + 0 x ^ { 3 } - 9 x ^ { 2 } +3 x + 6 \\ b ( x ) & : x ^ { 2 } + 0 x - 2
\end {align} $$

سپس، مشابه تقسیم اعداد، چندجمله‌ای $$ a ( x ) $$ را بر چندجمله‌ای $$ b ( x ) $$ تقسیم می‌کنیم.

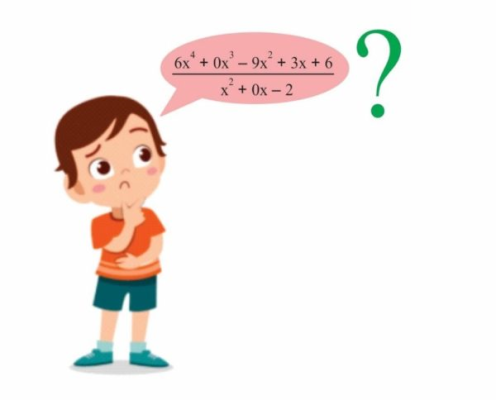
مرحله ۳: سپس اولین جمله مقسوم را بر اولین جمله مقسوم‌علیه تقسیم کنید. بنابراین، باید $$6 x^{4}$$ را بر $$x^2$$ تقسیم کنیم که حاصل آن $$ 6 x ^ 2 $$ است و می‌شود اولین جمله خارج قسمت.

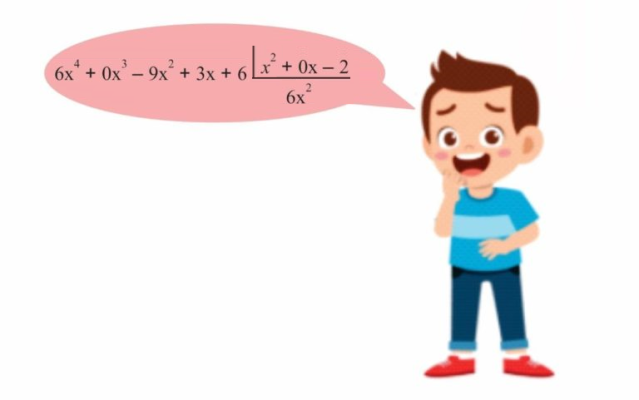
مرحله ۴: خارج قسمتِ به‌دست‌آمده در مرحله قبل را در مقسوم‌علیه ضرب کنید. یعنی، برای مثالی که داریم، باید $$ 6 x ^ 2 $$ را در مقسوم‌علیه ضرب کنیم که نتیجه آن برابر است با

$$ \large 6 x ^ { 2 } \times \left ( x ^ { 2} + 0 x - 2 \right ) = 6 x ^ { 4 } + 0 x ^ { 3 } - 1 2 x ^ { 2 } $$

مرحله 5: برای به‌دست آوردن مقسوم جدید، حاصل‌ضرب به‌دست‌آمده را از مقسوم کم کنید و نتیجه‌ را با رعایت ترتیب جمله‌ای با بیشترین درجه بنویسید.

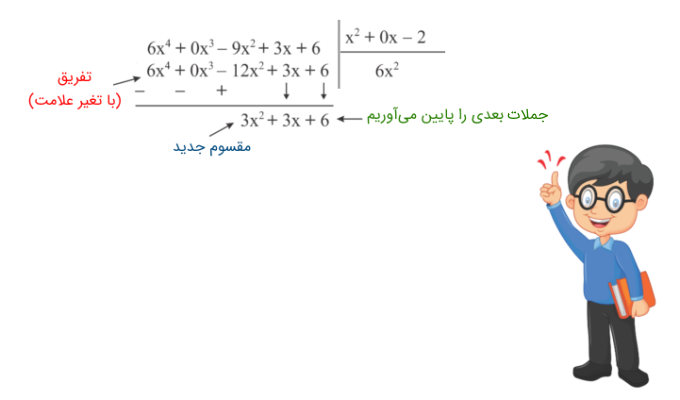
مرحله ۶: مراحل ۲ و ۳ و ۴ را تکرار کنید تا زمانی که جمله دیگری برای پایین آوردن وجود نداشته باشد. بدین ترتیب، جمله $$ 3 x ^ 2 $$ را بر $$ x ^ 2 $$، تقسیم می‌کنیم که حاصلش عدد $$ 3 $$ است و آن را به‌عنوان دومین جمله خارج قسمت می‌نویسیم.

توان مقسوم جدید ($$3x $$) برابر با $$1 $$ است. این عدد کمتر از توان مقسوم‌علیه ($$2$$) است. در نتیجه، باقیمانده غیرصفر را داریم.

نکته: از آنجا که باقیمانده غیرصفر است، می‌توانیم بگوییم $$ x ^ 2 - 2 $$ یک عامل برای $$6 x^{4}-9 x^{2}+3 x+6$$ نیست. اگر باقیمانده صفر باشد، می‌توانیم بگوییم $$ x ^ 2 - 2 $$ یکی عامل برای $$ 6 x^{4}-9 x^{2}+3 x+6 $$ است.

مثال‌های تقسیم عبارت های جبری

در این بخش، مثال‌هایی را از تقسیم عبارت‌های جبری حل می‌کنیم.

مثال اول تقسیم عبارت های جبری

عبارت جبری $$ 6 x y-4 y+6-9 x $$ را بر $$ 2 y-3 $$ تقسیم کنید.

حل: اگر به عبارت $$ 6 x y-4 y+6-9 x $$ دقت کنیم، می‌توانیم از $$ 2y $$ در دو جمله اول فاکتور بگیریم. همچنین می‌توانیم از $$ 3 $$ برای دو جمله بعدی فاکتور بگیریم. در نتیجه، عبارت به‌شکل زیر درمی‌آید:

$$ \large \begin {align} 6 x y-4 y+6-9 x & = 2 y ( 3 x - 2 ) - 3 ( 3 x - 2 )
\\
& = ( 2 y - 3) ( 3 x - 2 )
\end {align} $$

بنابراین، عبارت $$ 6 x y-4 y+6-9 x $$ را می‌توان به‌صورت ضرب عوامل $$ (2 y-3)(3 x-2) $$ نوشت. در نتیجه، خواهیم داشت:

$$ \large \frac { 6 x y - 4 y + 6 - 9 x } { ( 2 y - 3 ) } = \frac { ( 2 y - 3 ) ( 3 x - 2 ) } { ( 2 y - 3 ) } = ( 3 x - 2 ) $$

مثال دوم تقسیم عبارت های جبری

باقیمانده تقسیم $$ x^{4}+x^{3}-2 x^{2}+x+1 $$ بر $$ x - 1 $$ را به‌دست آورید.

حل: باید عبارت $$ x^{4}+x^{3}-2 x^{2}+x+1 $$ را بر $$ x - 1 $$ تقسیم کنیم. این تقسیم به‌صورت زیر انجام می‌شود:

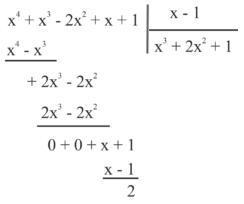
همان‌طور که می‌بینیم، خارج قسمت $$ x^{3}+2 x^{2}+1 $$ است و باقیمانده $$ 2 $$. در نتیجه، یاقیمانده تقسیم $$ x^{4}+x^{3}-2 x^{2}+x+1 $$ بر $$ x - 1 $$ برابر با $$ 2 $$ است.

مثال سوم تقسیم عبارت های جبری

عبارت $$ 16 x^{4} y^{2} $$ را بر $$ 4 x y^{2} $$ تقسیم کنید.

حل: در اینجا، دو تک‌جمله‌ای داریم که تقسیم آن‌ها را به‌‌صورت زیر انجام می‌دهیم:

$$ \large \begin {align} \frac { 1 6 x ^ { 4 } y ^ { 2 } }{ 4 x y ^ { 2 } } & = \frac { 1 6 \times x \times x \times x \times x \times y \times y } { 4 \times x \times y \times y } \\ & = 4 \times x \times x \times x = 4 x ^ { 3 } \end {align} $$

مثال چهارم تقسیم عبارت های جبری

با استفاده از روش تقسیم طولانی، چندجمله‌ای $$ 3 x^{2}-x^{3}-3 x+5 $$ را بر $$ x-1-x^{2} $$ تقسیم کنید.

حل: مقسوم $$ -x^{3}+3 x^{2}-3 x+5 $$ و مقسوم‌علیه $$ -x^{2}+x-1 $$ است. تقسیم را به‌صورت زیر انجام می‌دهیم:

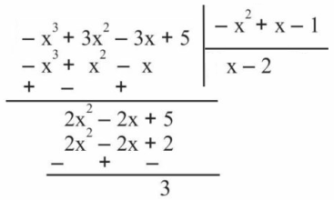
درجه عدد ثابت $$3$$ برابر با $$0$$ است که کمتر از درجه مقسوم‌علیه ($$-x^{2}+x-1 $$) است. بنابراین، تقسیم پایان می‌یابد و خارج قسمت برابر با $$ x - 2 $$ خواهد بود.

برای اعتبارسنجی تقسیم، از رابطه زیر استفاده می‌کنیم:

باقیمانده + (خارج قسمت × مقسم‌علیه) = مقسوم

بنابراین، خواهیم داشت:

$$ \large \begin {align} \left ( - x ^ { 2 } + x - 1 \right ) ( x - 2 ) + 3 & = - x ^ { 3 } + x ^ { 2 } - x + 2 x ^ { 2 } - 2 x + 2 + 3
\\ & = - x ^ { 3 } + 3 x ^ { 2 } - 3 x + 5
\end {align} $$

می‌بینیم که حاصل برابر با مقسوم است و تقسیم را به‌درستی انجام داده‌ایم.

مثال پنجم تقسیم عبارت های جبری

عبارت جبری $$ 12-14 a^{2}-13 a $$ را بر $$ 3+2 a $$ تقسیم کنید.

حل: مقسوم $$ -14 a^{2}-13 a+12 $$ و مقسوم‌علیه $$ 2 a+3 $$ است. بنابراین، تقسیم را به‌صورت زیر انجام می‌دهیم:

می‌بینیم که خارج قسمت $$ - 7 a + 4 $$ و باقیمانده $$ 0 $$ است.

مثال ششم تقسیم عبارت های جبری

عبارت $$ \frac { { { 3 }{ a } { b } { \left ( {4 } {a } ^ { 2 }{ b } ^ { 5 } \right ) } } } { { { 8 } { a } ^ { 2 } { b } ^ { 3 } } } $$ را ساده کنید.

حل: ابتدا جمله‌های صورت را در هم ضرب می‌کنیم:

$$ \large \frac { { { 1 2 } { a } ^ { 3 } { b } ^ { 6 } }} { { { 8 } { a } ^ { 2 } { b } ^ { 3 } } } $$

اگر به‌صورت ساده این تقسیم را بنویسیم، خواهیم داشت:

$$ \large \frac { { { 1 2 } \times { a } { a } { a } \times { b } { b} { b } { b } {b } { b } } } { { { 8 } \times { a } { a } \times { b }{ b } { b } } } $$

در ادامه، اعداد صورت و مخرج و همچنین، متغیرهایی را که متشابه هستند، با هم ساده می‌کنیم. در نتیجه، حاصل تقسیم به‌شکل زیر خواهد بود:

$$ \large \frac { { { 3 } { a } { b } ^ { 3 } } } { { 2 } } $$

مثال هفتم تقسیم عبارت های جبری

عبارت زیر را ساده کنید:

$$ \large \frac { { { 1 2 } { m } ^ { 2 } {n } ^ { 3 } } }{ { { \left ( { 6 } { m } ^ { 4 } { n } ^ { 5 } \right ) } ^ { 2 } } } $$

حل: ابتدا مخرج را به توان دو می‌رسانیم:

$$ \large \frac { { { 1 2 } { m } ^ { 2 } { n } ^ { 3 } } } { { { \left ( { 6 } { m } ^ { 4 } { n } ^ { 5 } \right ) } ^ { 2 } } } = \frac { { { 1 2 } { m } ^ { 2 } { n } ^ { 3 } } } { { { 3 6 }{ m } ^ { 8 } { n } ^ { 1 0 } } } $$

در ادامه، اعداد و متغیرهای صورت و مخرج را ساده می‌کنیم. بنابراین، جواب به‌صورت زیر است:

$$ \large \frac { 1 } { { { 3 } { m } ^ {6 } { n } ^ { 7 } } } $$

مثال هشتم تقسیم عبارت های جبری

تقسیم زیر را انجام دهید:

$$ \large \frac { { { 6 } { p } ^ { 3 } { q } ^ { 2 } - { 1 0 } { p } ^ { 2 } { q } } } { { { 4 } { q } } } $$

حل: برای سادگی، کسر را به دو کسر می‌شکنیم که در هر دوی آن‌ها مخرج $$ 4 q $$ است. بنابراین، داریم:

$$ \large \frac { { { 6 } { p } ^ { 3 } { q } ^ { 2 } - { 1 0 } { p } ^ { 2 } { q } } } { { { 4 } { q } } } = \frac { { { 6 } { p } ^ { 3 } { q } ^ { 2 } } } { { { 4 } { q } } } - \frac { { { 1 0 }{ p } ^ { 2 } { q } } } { { { 4 } { q } } } $$

در ادامه، متغیرها و اعداد صورت و مخرج را ساده می‌کنیم:‌

$$ \large \frac { {{ 3 } { p} ^{ 3 } { q }} } { { 2 } } - \frac { { { 5 } { p } ^ { 2 } } } { { 2 } } $$

در نهایت، جواب این‌گونه خواهد بود:

$$ \large \frac { { { 3 } { p } ^ { 3 } { q } - {5 } { p } ^ { 2 } } } {{ 2 } } $$

مثال نهم تقسیم عبارت های جبری

تقسیم زیر را حل کنید:

$$ \large \frac { { { 3 } + \frac { 1 } { { x } } } } { { \frac { 5 } { { x } } + { 4 } } } $$

حل: این مثال را می‌توانیم به دو روش حل کنیم.

روش ۱: ابتدا هم مقسوم و هم مقسوم‌علیه را به یک کسر تبدیل می‌کنیم:‌

$$ \large { 3 } + \frac { 1 } { { x } } = \frac { { { 3 } { x } + { 1 } } } { { x } }, \;\;\;\; \frac{5}{{x}}+{4}=\frac{{{5}+{4}{x}}}{{x}} $$

بنابراین، تقسیم به‌شکل زیر درمی‌آید:

$$ \large \frac { { { 3 } + \frac { 1 } { { x } } } } { { \frac { 5 } { { x } } + { 4 } } } = \frac { { \frac { { { 3 } { x } + { 1 } } } { { x } } } } { { \frac { { { 5 } + { 4 } { x } } } { { x } } } } $$

که می‌توان آن را به صورت زیر نوشت:

$$ \large \frac { { { 3 } { x } + { 1 } } } { { x } } \div \frac { { { 5 } + { 4 } { x } } } { { x } } $$

در آموزش «تقسیم کسرها — به زبان ساده + حل تمرین و مثال» دیدیم که برای انجام تقسیم کسرها، کسر اول (مقسوم) را در معکوس کسر دوم (مقسوم‌علیه) ضرب می‌کنیم. در اینجا نیز چنین کاری انجام می‌دهیم و خواهیم داشت:

$$ \large \frac { { { 3 } { x } + { 1 } } } { { { x } } } \times \frac { x } { { { 5 } + { 4 } { x } } } = \frac { { { 3 } { x } + { 1 } } } { { { 5 } + { 4 } { x } } } $$

این تقسیم را نمی‌توان از این ساده‌تر کرد.

روش ۲: در یک روش دیگر، می‌توانیم صورت و خرج را در $$ x $$ ضرب کنیم. در نتیجه، به‌سادگی خواهیم داشت:

$$ \large \frac { { { 3 } + \frac { 1 } { { x } }} } { { \frac { 5 } { { x } } + { 4 } } } \times \frac { x } { { x } } = \frac { { { 3 } { x } + { 1 } } } { { { 5 } + { 4 } { x } } } $$

که نمی‌توان آن را از این ساده‌تر کرد.

مثال دهم تقسیم عبارت های جبری

حاصل تقسیم زیر را به‌دست آورید:

$$ \large \frac { { { 6 } { x } ^ { 2 } + { 6 } + { 7 } { x } } } { { { 2 } { x } + { 1 } } } $$

حل: از روش تقسیم طولانی استفاده می‌کنیم.

مرحله ۱: تقسیم $$ 6 x ^ 2 ÷ 2 x = 3 x $$

اکنون حاصل‌ضرب $$ ( 3 x ) ( 2 x + 1 ) = 6 x ^ 2 + 3x $$ را نوشته و آن را زیر مقسوم می‌نویسیم:

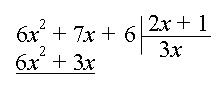
مرحله ۲: عبارت $$ 6 x ^ 2 + 3 x $$ را از مقسوم کم می‌کنیم:

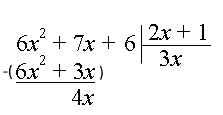
مرحله ۳: اکنون عدد $$6$$ را پایین می‌آوریم:

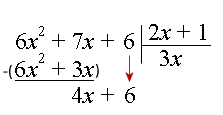
مرحله ۴: $$ 4 x $$ را بر $$ 2 x $$ تقسیم می‌کنیم. جواب $$ 2 $$ است. با ضرب $$ 2 $$ در $$ 2 x + 1 $$، مقدار $$ 2 ( 2 x + 1 ) = 4 x + 2 $$ را داریم که زیر $$ 4 x + 6 $$ آن را می‌نویسیم.

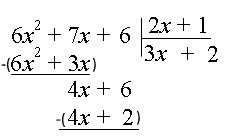
مرحله ۵: اکنون $$ 4 x + 2 $$ را از $$ 4 x + 6 $$ کم می‌کنیم که نتیجه $$ 4 $$ می‌شود. می‌بینیم درجه $$ 4 $$ از $$ 2 x + 1 $$ کمتر است و تقسیم پایان می‌یابد.

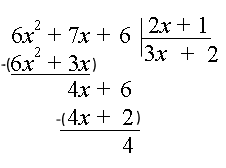
در نهایت، اگر حاصل تقسیم به‌صورت زیر درمی‌آید:

$$ \large \frac { { { 6 } { x } ^ { 2 } + { 6 } + { 7 } { x } }} { { { 2 } { x } + { 1 } } }= { 3 } { x } +{ 2 } + \frac { 4 } { { { 2 } { x } + { 1 } } } $$

مراحل انجام تقسیم به‌صورت زیر است:

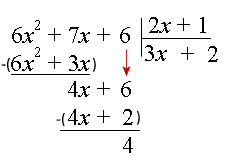
معرفی فیلم آموزش ریاضی پایه هفتم