روش نیوتن — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، روش حل معادلات درجه دوم، معادلات درجه سوم، معادلات مثلثاتی و معادلات رادیکالی را بیان کردیم و دیدیم با قواعد خاصی، به‌سادگی می‌توان جواب این معادلات را به‌دست آورد. اما حل برخی معادلات را نمی‌توان به‌آسانی و به‌صورت تحلیلی به‌دست آورد. بنابراین، باید از روش‌های عددی برای حل آن‌ها کمک گرفت. یکی از این روش‌های عددی که در آن از مشتق‌گیری استفاده می‌شود و در زمینه‌های مختلفی به‌کار می‌رود، روش نیوتن است. «روش نیوتن» که با نام «روش نیوتن رافسون» نیز شناخته می‌شود، روشی عددی و تقریبی برای حل معادلات است. در ادامه، این روش را معرفی خواهیم کرد.

فرض کنید می‌خواهیم جواب تقریبی معادله $$f\left( x \right) = 0$$ را پیدا کنیم. همچنین فرض کنید تقریب اولیه جواب معادله را $$x_0$$ می‌نامیم. این تقریب اولیه ممکن است مناسب نباشد، البته این طبیعی است زیرا یک حدس اولیه سریع است. بنابراین باید تقریب بهتری را پیدا کنیم. برای این کار، خط مماس بر $$f\left( x \right)$$ را در نقطه $$x_0$$ در نظر بگیرید:

$$y = f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)$$

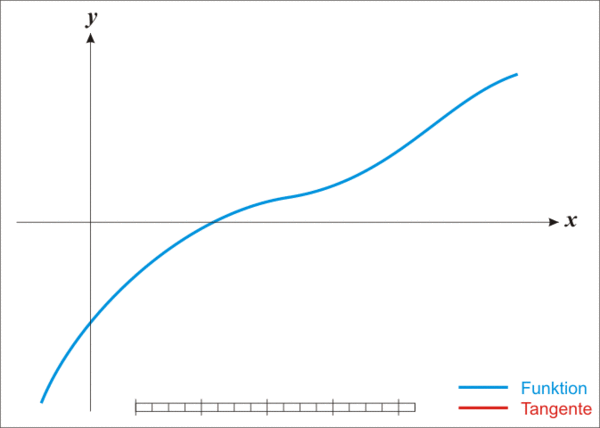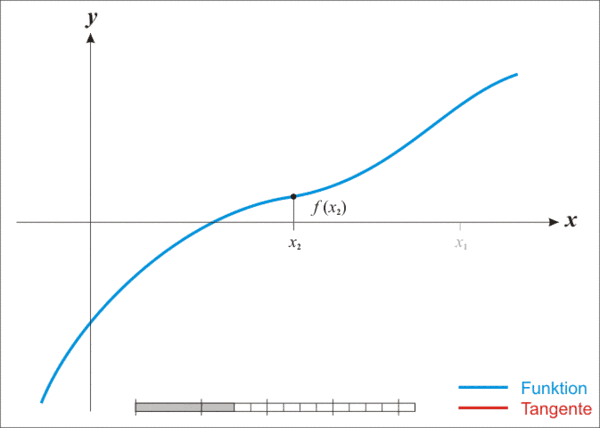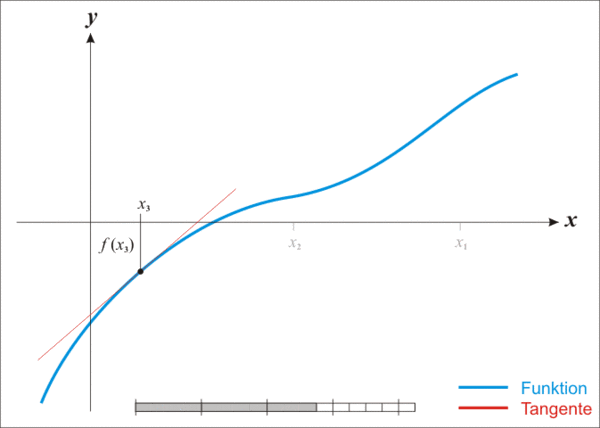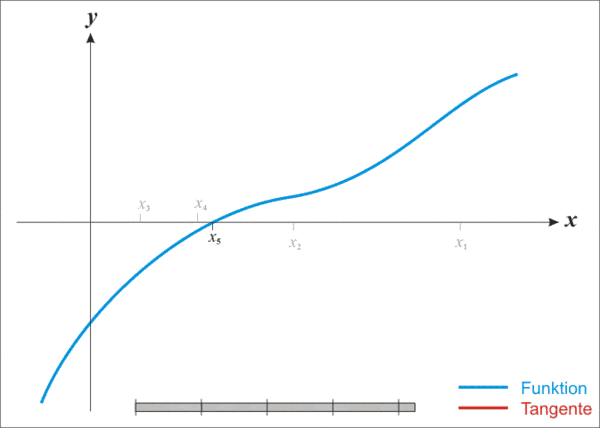
اکنون به شکل زیر دقت کنید:

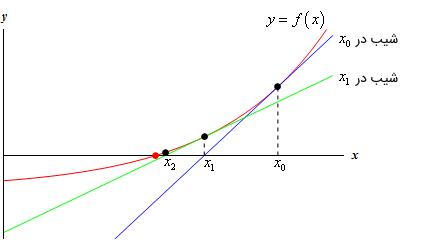
خط آبی‌رنگ، خط مماس بر منحنی $$f(x)$$ در نقطه $$x_0$$ است. از شکل بالا مشاهده می‌شود که این خط در نقطه‌ای نزدیک‌تر به جواب واقعی، محور $$x$$ را قطع می‌کند (نقطه $$x_1$$ نسبت به نقطه $$x_0$$ به جواب نزدیک‌تر است). همان‌طور که از شکل بالا مشخص است، نقطه $$x_1$$ به جواب واقعی نزدیک‌تر است، بنابراین، $$x_1$$ را به‌عنوان تقریب جدید جواب در نظر می‌گیریم. اما چگونه نقطه $$x_1$$ را پیدا کنیم؟ همان‌گونه که مشاهده می‌کنیم، مختصات نقطه مورد نظر $$(x_1, 0)$$ است و می‌دانیم که در خط مماس بر منحنی $$f(x)$$ در نقطه $$x_0$$ صدق می‌کند. بنابراین، به‌سادگی می‌توان نقطه $$x_1$$ را محاسبه کرد:

$$\begin{align*}0 & = f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)\left( {{x_1} - {x_0}} \right)\\ {x_1} - {x_0} & = - \frac{{f\left( {{x_0}} \right)}}{{f'\left( {{x_0}} \right)}}\\ {x_1} & = {x_0} - \frac{{f\left( {{x_0}} \right)}}{{f'\left( {{x_0}} \right)}}\end{align*}$$

البته باید دقت کرد که مشتق تابع $$f$$ در نقطه مورد نظر صفر نشود. تا این‌جا تقریب $$x_1$$ را نیز محاسبه کرده‌ایم. برای آنکه تقریب به جواب واقعی نزدیک شود، باید این فرایند را ادامه دهیم. بنابراین، خط مماس بر $$f\left( x \right)$$ را در نقطه $$x_1$$ تشکیل می‌دهیم و نقطه برخورد آن با محور $$x$$ را به‌عنون جواب تقریبی جدید در نظر می‌گیریم. این جواب تقریبی از رابطه زیر به‌دست می‌آید:

$${x_2} = {x_1} - \frac{{f\left( {{x_1}} \right)}}{{f'\left( {{x_1}} \right)}}$$

نقطه $$x_2$$ در شکل بالا نشان داده شده است. اگر فرایندی را که دو بار انجام دادیم ادامه دهیم، پاسخ به مقدار واقعی نزدیک و نزدیک‌تر می‌شود. این فرایند، «روش نیوتن» (Newton’s Method) نامیده می‌شود.

روش نیوتن

اگر $$x_n$$ یک تقریب برای جواب $$f\left( x \right) = 0$$ باشد، و اگر $$f'\left( {{x_n}} \right) \ne 0$$، تقریب بعدی از رابطه زیر قابل محاسبه است:

$${x_{n + 1}} = {x_n} - \frac{{f\left( {{x_n}} \right)}}{{f'\left( {{x_n}} \right)}}$$

اما ممکن است این پرسش پیش آید که چه زمانی باید محاسبات را متوقف کنیم؟ چند بار روش نیوتن را تکرار کنیم؟ یکی از معیارهای توقف این است که محاسبات را تا جایی ادامه دهیم که دو مورد از تقریب‌ها تا تعداد رقم اعشار مورد نظر با هم برابر شوند.

فیلم آموزش محاسبات عددی – مرور و حل مساله در فرادرس

کلیک کنید

قبل از آنکه مثال‌هایی درباره روش نیوتن ارائه دهیم، لازم است دو نکته را بیان کنیم. اول اینکه، معادله باید به‌فرم $$f\left( x \right) = 0$$ باشد. البته موضوع مهم‌تر این است که معادله به‌گونه‌ای باشد که بتوان از روش نیوتن برای حل آن استفاده کرد.

موضوع دوم، انتخاب حدس اولیه $$x_0$$ است. یکی از راه‌های پیشنهاد حدس اولیه مناسب، رسم نمودار تابع است. یک روش متداول دیگر، این است که اگر می‌دانیم جواب در بازه‌ای بین دو نقطه قرار دارد، نقطه میانی آن دو نقطه را به‌عنوان حدس اولیه برگزینیم.

مثال‌های زیر، کاربرد روش نیوتن را نشان می‌دهند.

مثال ۱

با استفاده از روش نیوتن، پاسخ معادله $$\cos x = x$$ را که در بازه $$\left[ {0,2} \right]$$ قرار دارد، پیدا کنید. پاسخ را تا شش رقم اعشار بیابید.

حل: همان‌گونه که در سؤال بیان شده، پاسخ در بازه $$\left[ {0,2} \right]$$ قرار دارد. بنابراین، طبق آن‌چه گفتیم، نقطه میانی این بازه، یعنی $${x_0} = 1$$‌ را به‌عنوان حدس اولیه در نظر می‌گیریم.

در ادامه، باید معادله را به‌شکل $$f\left( x \right) = 0$$ بنویسیم. بنابراین، داریم:

$$\cos x - x = 0$$

اکنون می‌توانیم فرمول عمومی روش نیوتن را بنویسیم:

$${x_{n + 1}} = {x_n} - \frac{{\cos x - x}}{{ - \sin x - 1}}$$

بنابراین، تقریب اول به‌صورت زیر به‌دست می‌آید:

$${x_1} = 1 - \frac{{\cos \left( 1 \right) - 1}}{{ - \sin \left( 1 \right) - 1}} = 0.7503638679$$

توجه کنید شش رقم اعشار، به این معنی نیست که $$x_1$$ را تا شش رقم اعشار بنویسیم و محاسبات را متوقف کنیم، بلکه باید محاسبات را تا جایی ادامه دهیم که دو تقریب متوالی، تا شش رقم اعشار با هم برابر باشند.

بنابراین، محاسبات را ادامه می‌دهیم:

$${x_2} = 0.7503638679 - \frac{{\cos \left( 0.7503638679 \right) - 0.7503638679}}{{ - \sin \left( {0.7503638679} \right) - 1}} = 0.7391128909$$

عدد بالا نشان می‌دهد که دو تقریب متوالی، تا یک رقم اعشار با هم برابر هستند، در نتیجه، باید روش نیوتن را برای رسیدن به هدف مورد نظر ادامه دهیم. اگر محاسبات را انجام دهیم، تقریب بعدی به‌صورت زیر به‌دست می‌آید:

$${x_3} = 0.7390851334$$

می‌بینیم که تقریب بهتر شده و دو تقریب اخیر، تا سه رقم اعشار با هم برابر هستند. باز هم فرایند را ادامه می‌دهیم. بنابراین، داریم:

$${x_4} = 0.7390851332$$

با نگاهی به $$x_4$$ می‌بینیم که به هدف خود رسیده‌ایم و دو تقریب $$x_3$$ و $$x_4$$، تا نُه رقم اعشار با هم برابر هستند. بنابراین، عملیات را متوقف می‌کنیم. در نهایت، پاسخ تقریبی معادله برابر با $${x_4} = 0.7390851332$$ است.

در مثال بالا دیدیم برای یافتن پاسخ با دقت تقریباً مناسب، محاسبات زیادی لازم نبود. اما همیشه این‌گونه نیست؛ گاهی لازم است برای رسیدن به دقت مناسب، تکرارهای زیادی را انجام داد. البته گاهی هم محاسبات با شکست مواجه می‌شود.

مثال زیر، ساده به‌نظر می‌رسد، اما نمونه خوبی برای اثبات گفته بالا است.

مثال ۲

با در نظر گرفتن حدس اولیه $${x_0} = 1$$، پاسخ تقریبی معادله $$\sqrt[3]{x} = 0$$ را به‌دست آورید.

حل:‌ واضح است که جواب معادله بالا $$x=0$$ است. اما می‌خواهیم ببینیم اعمال روش نیوتن برای این معادله به چه جوابی ختم می‌شود. فرمول عمومی روش نیوتن به‌صورت زیر است:

$${x_{n + 1}} = x_{n} - \frac{{{x_n}^{\frac{1}{3}}}}{{\frac{1}{3}{x_n}^{ - \frac{2}{3}}}} = {x_n} - 3{x_n} = - 2{x_n}$$

در حقیقت، این‌جا به محاسبات نیازی نیست. نتیجه هر تکرار، از پاسخ $$x=0$$ دور و دورتر می‌شود. جواب‌های چند تکرار اول به‌صورت زیر هستند:

$$\begin{align*}{x_1} & = - 2\\ {x_2} & = 4\\ {x_3} & = - 8\\ {x_4} & = 16\\ & etc. \end{align*}$$

در نتیجه، روش نیوتن با شکست مواجه شده و همگرا نمی‌شود. بنابراین باید دقت کنیم که در روش نیوتن، معمولاً جواب تقریبی معادله  با محاسبات و صرف زمان کمی به‌دست می‌آید. با این حال، گاهی باید محاسبات زیادی انجام دهیم یا اینکه محاسبات با شکست مواجه می‌شود.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• معادله خط — به زبان ساده
• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• دستگاه معادلات خطی — به زبان ساده
• جذر یا محاسبه ریشه دوم عدد — به زبان ساده

^^