جمع اعداد مخلوط — به زبان ساده + حل تمرین و مثال
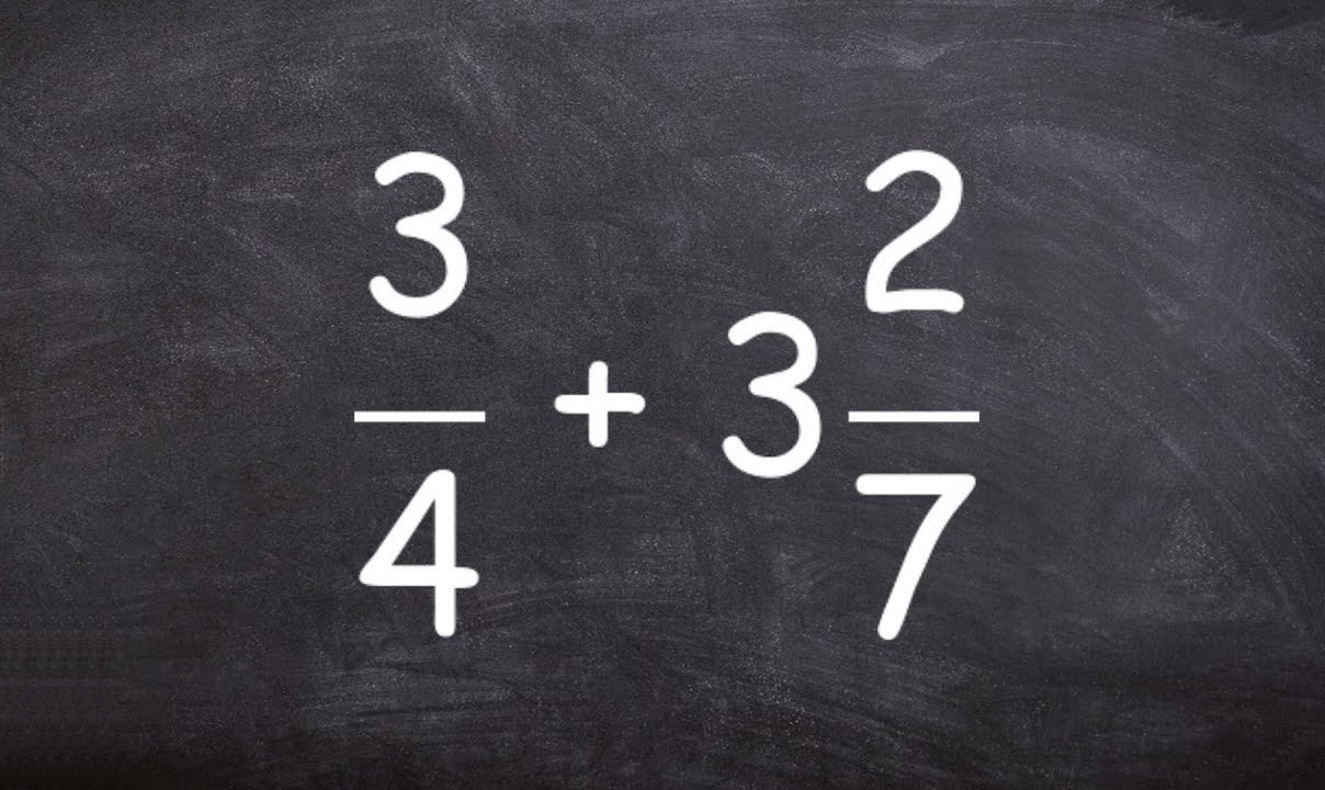
در آموزشهای پیشین مجله فرادرس، با اعداد مخلوط آشنا شدیم. در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، ضمن مروری کوتاه بر اعداد مخلوط، درباره جمع اعداد مخلوط بحث میکنیم و مثالهایی را بررسی خواهیم.
عدد مخلوط چیست؟
همانطور که در آموزشهای قبلی گفتیم، عدد مخلوط یا عدد آمیخته عددی است که از یک عدد صحیح و یک کسر (که صورت آن از مخرجش کوچکتر است) تشکیل شده است. اعداد زیر عدد مخلوط هستند:
$$ \large 1 \frac 12,\;\; 5\frac {12}{13},\;\; 3 \frac 59 $$
جمع اعداد مخلوط با مخرج برابر
جمع اعداد مخلوط با مخرج برابر بهسادگی قابل انجام است. با دو روش میتوان این کار را انجام داد.
- جمع بخش صحیح بهصورت جدا و بخش کسری بهصورت جدا
- تبدیل اعداد مخلوط به اعداد کسری و جمع آنها
روش اول جمع اعداد مخلوط با مخرج برابر
در روش اول، ابتدا دو عدد صحیح را با هم جمع میکنیم، سپس کسرها را با هم جمع میزنیم.
برای مثال، فرض کنید میخواهیم دو عدد زیر را با هم جمع کنیم:
$$ \large 4 \frac 17 + 1 \frac 2 7 $$
برای این کار، ابتدا دو عدد صحیح را با هم جمع میکنیم:
$$ \large 4 + 1 = 5 $$
سپس کسرها را با هم جمع میکنیم:
$$ \large \frac 17 + \frac 2 7 = \frac {1+2}{7} = \frac 37 $$
در نهایت، دو عدد را جمع میکنیم:
$$ \large 5 + \frac 37 = 5 \frac 37 $$
روش دوم جمع اعداد مخلوط با مخرج برابر
در این روش، ابتدا اعداد مخلوط را به کسر تبدیل میکنیم، سپس بهسادگی، آن دو کسر را جمع میکنیم. در نهایت، عدد کسری حاصل را به عدد مخلوط تبدیل میکنیم.
برای مثال، فرض کنید میخواهیم جمع دو عدد زیر را انجام دهیم:
$$ \large 3 \frac 25 + \frac 15 $$
عدد نخست یک عدد مخلوط است که باید آن را به یک عدد کسری تبدیل کنیم. عدد دوم خودش یک کسر است و نیازی به تبدیل ندارد. عدد دوم را اینگونه مینویسیم:
$$ \large 3 \frac 25 = 3 + \frac 25= \frac {3\times 5}{5}+\frac 25 =\frac {15}5+\frac 25 = \frac {15+2}{5}=\frac {17}{5} $$
بنابراین، باید جمع زیر را محاسبه کنیم:
$$ \large\frac 15 + \frac {17}{5} $$
که حاصل آن برابر است با
$$ \large\frac 15 + \frac {17}{5} =\frac {1+17}5=\frac {18}5 $$
در گام نهایی، عدد کسری حاصل را به عدد مخلوط تبدیل میکنیم:
$$ \large \frac { 18 } 5 = \frac { 15+3} {5}=\frac {15}{5}+\frac {3}{5}=3 + \frac 35 = 3\frac 35$$
جمع اعداد مخلوط با مخرج نابرابر
وقتی مخرجها برابر نباشد، باید از مخرج مشترک کمک بگیریم. در این حالت نیز، میتوانیم با دو روش جمع اعداد مخلوط را انجام دهیم.
روش اول جمع اعداد مخلوط با مخرج نابرابر
در روش اول جمع اعداد مخلوط ابتدا اعداد صحیح آنها را جدا با هم جمع میکنیم، سپس کسرهایشان را با هم جمع میکنیم و حاصل را با آن جمع میبندیم. چون در این حالت، مخرجها با یکدیگر برابر نیست، باید از آنها مخرج مشترک بگیریم و سپس جمعشان کنیم. با یک مثال، جمع اعداد مختلط با مخرج نابرابر را توضیح میدهیم.
فرض کنید میخواهیم جمع زیر را انجام دهیم:
$$ \large 3 \frac 14 + 2 \frac 13 $$
طبق آنچه گفتیم، ابتدا دو عدد صحیح را جمع میکنیم:
$$ \large 3+2 = 5 $$
اکنون نوبت کسرهاست که آنها را با هم جمع کنیم:
$$ \large \frac 14 + \frac 13 $$
چون که مخرج کسرها یکسان نیست، باید مخرج مشترک بگیریم و آنها را جمع کنیم. کوچکترین مضرب مشترک دو عدد $$3$$ و $$4$$، عدد $$12$$ است که میشود مخرج مشترک دو کسر. پس، جمع دو کسر بهشکل زیر انجام میشود:
$$ \large \frac 14 + \frac 13= \frac {1\times 3}{12}+\frac{1\times 4} {12} = \frac {3+4}{12}= \frac{7}{12}$$
اکنون هم جمع دو عدد صحیح را داریم و هم حاصلجمع دو کسر را. بنابراین، جواب نهایی جمع دو عدد مخلوط بهشکل زیر است:
$$ \large 3\frac 14 + 2\frac 13= (3+2)+ (\frac 14+\frac 13)= 5 + \frac {7}{12}=5\frac{7}{12}$$
میتوانیم عدد مخلوط جواب را به یک عدد کسری تبدیل کنیم:
$$ \large 5\frac{7}{12}=5+\frac {7}{12}=\frac {5\times 12}{12}+\frac {7}{12}=\frac {60}{12}+\frac {7}{12}=\frac {67}{12}$$
برای آشنایی با مخرج مشترک، پیشنهاد میکنیم به آموزش «مخرج مشترک چیست ، چگونه مخرج مشترک بگیریم؟ — به زبان ساده» مراجعه کنید.
اکنون یک مثال دیگر را با هم حل میکنیم. میخواهیم حاصلِ جمع زیر را بهدست آوریم:
$$ \large 4 \frac 35 + 3 \frac 12 $$
مانند مثال قبل عمل میکنیم. ابتدا اعداد صحیح را با هم جمع کرده، سپس کسرها را با هم جمع میکنیم.
جمع دو عدد صحیح برابر است با:
$$ \large 4 + 3 = 7 $$
برای جمع دو کسر، ابتدا مخرج مشترک میگیریم:
$$\large \begin{align} \frac 35 + \frac 12 & = \frac {3 \times2}{5 \times2} + \frac {1\times 5}{2\times 5} =\frac {6}{10}+\frac {5}{10}\\
& = \frac {6+5} {10}=\frac {11}{10}
\end {align} $$
با توجه به اینکه کسر حاصل یک کسر ناسره است (یعنی صورتش از مخرجش بزرگتر از یک است و در واقع، کسر بزرگتر از از واحد است)، میتوانیم آن را به یک عدد مخلوط تبدیل کنیم:
$$\large \begin{align}
\frac {11}{10}= \frac {10+1} {10} = \frac {10}{10}+\frac {1}{10}=1 + \frac {1} { 10}
\end {align} $$
در گام آخر، باید دو حدد حاصل از جمع اعداد صحیح و اعداد کسری را با هم جمع کنیم:
$$\large \begin{align}
(7)+(1 + \frac {1} { 10} )=7+1+\frac {1}{10}=8+\frac {1}{10}
\end {align} $$
روش دوم جمع اعداد مخلوط با مخرج نابرابر
در این روش، ابتدا اعداد مخلوط را به کسر تبدیل میکنیم، سپس برای کسرها مخرج مشترک میگیریم و جمعشان میکنیم. در نهایت نیز، عدد کسری بهدستآمده را به عد مخلوط تبدیل میکنیم. با یک مثال این موضوع را شرح میدهیم.
میخواهیم جمع $$ 1\frac 23 +1\frac 14 $$ را محاسبه کنیم. ابتدا، دو عدد را بهصورت کسر مینویسیم:
$$ \large \begin {align} 1 \frac 2 3 + 1 \frac 1 4 &= ( \frac { 1 \times 3 } 3 + \frac 2 3 ) + ( \frac { 1 \times 4 } 4 +\frac 1 4 ) \\ &= \frac { 3 + 2 } { 3 } + \frac { 4 + 1 } { 4 } = \frac 53 + \frac 5 4
\end {align} $$
سپس، از آنجا که مخرجها متفاوت هستند، مخرج مشترک میگیریم. ک.م.م دو عدد $$3$$ و $$4$$، عدد $$12$$ است. جمع دو کسر بهصورت زیر خواهد بود:
$$\large \frac {5 \times 4}{3\times 4 }+ \frac {5 \times 3 }{4 \times 3 } = \frac {20}{12} + \frac {15}{12}= \frac {35}{12} $$
اکنون باید این کسر را به یک عدد مخلوط تبدیل کنیم:
$$ \large \begin {align} \frac {35} {12} = \frac {24+11}{12}= \frac {24}{12}+\frac {11}{12}=2+\frac {11}{12} = 2\frac {11}{12} \end {align} $$
جمع اعداد مخلوط با شکل
برای جمع اعداد مخلوط (با مخرج یکسان) با کمک شکل، ابتدا، یک شکل واحد رسم میکنیم که نشانه عدد $$1$$ است. سپس مخرج کسرها را میبینیم. مثلاً اگر مخرج کسرها $$3$$ بود، شکلها را به سه قسمت مساوی تقسیم میکنیم. سپس، برای هر عدد صحیح شکل کامل و برای هر کسر، تعداد تکه متناظر از شکل اصلی را در نظر میگیریم. مثلاً اگر یک عدد $$1\frac 13 $$ باشد، یک شکل کامل و یک تکه یکسومی از آن را مشخص میکنیم. برای اعداد دیگر نیز همین کار را میکنیم. در نهایت، تعداد شکلهایی که کامل هستند و تعداد تکهها را میشماریم.
برای مثال، در شکل زیر، دو عدد $$1\frac 23 $$ و $$2 \frac 13 $$ با هم جمع شدهاند.
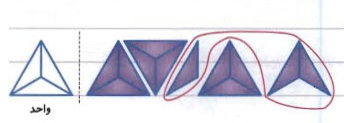
از چپ، دو واحد و یک تکه (یکسوم) را میبینیم که نماینده عدد $$2 \frac 13 $$ است. در سمت راست نیز یک مثلث کامل و یک تکه دوتایی عدد $$1\frac 23 $$ را نشان میدهند. اگر مجموع همه اینها را بشماریم، میبینیم که سه مثلث کامل داریم و سه تکه. خود سه تکه یک مثلث کامل را تشکیل میدهند. در نتیجه، چهار مثلث کامل داریم که میشود عدد $$4$$. یعنی، جواب بهصورت زیر خواهد بود:
$$ \large 2 \frac 13 + 1 \frac 23 = 4 $$
جمع اعداد مخلوط روی محور اعداد
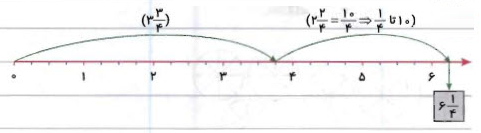
برای محاسبه جمع اعداد مخلوط روی محور اعداد، اول از همه، عدد نخست را روی محور مشخص میکنیم. این کار را با کمان جهتدار انجام میدهیم. سپس، از انتهای این کمان، بهاندازه عدد دوم یک کمان دیگر رسم میکنیم. حاصلجمع، برابر با طول کمان از ابتدای کمان مربوط به عدد نخست تا انتهای کمان دوم است.
برای مثال، جمع $$3\frac 34 + 2\frac 24 $$ با کمک محور اعداد، برابر با $$6\frac 14 $$ خواهد بود:
مثالهای جمع اعداد مخلوط
در این بخش، چند مثال را از جمع اعداد مخلوط حل میکنیم.
مثال اول جمع اعداد مخلوط
با استفاده از شکل، جمع دو عدد $$1 \frac 34 $$ و $$1\frac 24 $$ را محاسبه کنید.
حل: برای هر واحد یک دایره در نظر میگیریم و با توجه به مخرج کسر، آن را به چهار قسمت مساوی تقسیم میکنیم. برای عدد $$1 \frac 34 $$ یک دایره کامل و سه بخش آن را در نظر میگیریم و عدد $$1\frac 24 $$ را با یک دایره و دو بخش کوچک آن مشخص میکنیم.
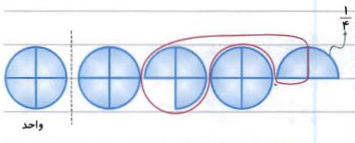
میبینیم که سه دایره کامل و یک بخش کوچک از آن را داریم. بنابراین، جواب بهصورت زیر است:
$$\large 1\frac 34 + 1 \frac 2 4 = 3 \frac 1 4 $$
مثال دوم جمع اعداد مخلوط
با کمک محور اعداد، حاصلجمع $$2 \frac 35 + 3 $$ را محاسبه کنید.
حل: ابتدا $$2\frac 35 $$ را روی محور مشخص میکنیم و سپس در ادامه آن، عدد $$3$$ را نمایش میدهیم. شکل زیر جمع را نشان میدهد.
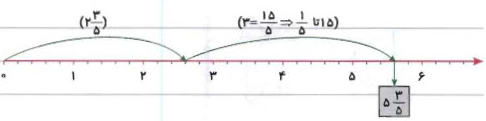
میبینیم که جواب برابر با $$5 \frac 35 $$ است.
مثال سوم جمع اعداد مخلوط
حاصلجمع $$ 3 \frac { 5 } { 8 } + 2 \frac { 2 } { 3 } $$ را محاسبه کنید.
حل: برای بهدست آوردن جواب، اعداد صحیح را جدا، و اعداد کسری را جدا با هم جمع میکنیم:
$$ \large \begin {aligned}
& 3 \frac { 5 } { 8 } + 2 \frac { 2 } { 3 } \\
& = ( 3 + 2 ) + \left ( \frac { 5 } { 8 } + \frac { 2 } { 3 } \right ) \\
& = 5 + \left ( \frac { 5 } { 8 } + \frac { 2 } { 3 } \right )
\end {aligned} $$
میبینیم که دو عدد کسری، مخرج یکسانی ندارند. بنابراین، باید مخرج مشترک بگیریم و آن دو را با هم جمع کنیم. ک.م.م دو عدد $$3$$ و $$8$$، عدد $$24$$ است که مخرج مشترک دو کسر میشود. مراحل زیر، نحوه محاسبه جواب نهایی را نشان میدهند:
$$ \large \begin {aligned}
& = 5 + \frac { 5 \times 3 } { 8 \times 3 } + \frac{ 2 \times 8} { 3 \times 8 } \\
& = 5 + \frac { 1 5 } { 2 4 } + \frac { 1 6 } { 2 4 } \\
& = 5 + \frac { 1 5 + 1 6 } { 2 4 } \\
& = 5 + \frac { 3 1 } { 2 4 } \\
& = 5 + 1 \frac { 7 } { 2 4 } \\
& = 6 \frac { 7 } { 2 4 }
\end {aligned} $$
مثال چهارم جمع اعداد مخلوط
جمع سه عدد $$1 \frac{1}{6}$$ و $$2 \frac{1}{8}$$ و $$3 \frac{1}{4}$$ را محاسبه کنید.
حل: باید حاصلجمع $$ 1 \frac { 1 } { 6 } + 2 \frac { 1 } { 8 } + 3 \frac { 1 } { 4 } $$ را بهدست آوریم. مطابق آنچه پیشتر نیز انجام دادیم، اعداد صحیح را جدا و کسرها را جدا با هم جمع میکنیم. چون مخرج کسرها (اعداد $$4$$ و $$6$$ و $$8$$) یکسان نیستند، باید مخرج مشترک بگیریم. مخرج مشترک عدد $$24$$ است. در نتیجه، خواهیم داشت:
$$ \large
\begin {aligned}
& = ( 1 + 2 + 3 ) + \left ( \frac { 1 } { 6} + \frac { 1 } { 8 } + \frac { 1 } { 4 } \right ) \\
& = 6 + \left ( \frac { 1 } { 6 } + \frac { 1 } { 8 } + \frac { 1 }{ 4 } \right ) \\
& = 6 + \frac { 1 \times 4 } { 6 \times 4 } + \frac { 1 \times 3 } { 8 \times 3 } + \frac { 1 \times 6 } { 4 \times 6 } \\
& = 6 + \frac { 4} { 2 4 } + \frac { 3 } { 2 4 } + \frac { 6 } { 2 4 } \\
& = 6 + \frac { 4 + 3 + 6 } { 2 4 } \\
& = 6 + \frac { 1 3 } { 2 4 } \\
& = 6 \frac { 1 3 } { 2 4 }
\end {aligned} $$
مثال پنجم جمع اعداد مخلوط
جمع $$ 2 \frac { 3 } { 9 } + 1 \frac { 1 } { 6 } + 2 \frac { 2 } { 3 } $$ را محاسبه کنید.
حل: این مثال را با روش دیگری حل میکنیم. بهجای آنکه اعداد صحیح را جدا و کسرها را جدا جمع کنیم، ابتدا اعداد مخلوط را به کسر تبدیل و سپس جمعشان میکنیم. مخرج مشترک سه کسر $$18$$ است. جواب بهشکل زیر محاسبه میشود:
$$\begin{aligned}
& 2 \frac { 3 } { 9 } + 1 \frac { 1 } { 6 } + 2 \frac { 2 } { 3 } \\
& = \frac { ( 9 \times 2 ) + 3 } { 9 } + \frac { ( 6 \times 1 ) + 1 } { 6 } + \frac { ( 3 \times 2 ) + 2 } { 3 } \\
& = \frac { 2 1 } { 9 } + \frac { 7 } {6 } + \frac { 8 } { 3 } \\
& = \frac { 2 1 \times 2 } { 9 \times 2 } + \frac { 7 \times 3 } { 6 \times 3 } + \frac { 8 \times 6 } { 3 \times 6 } \\
& =\frac { 4 2 } { 1 8 } + \frac { 2 1 } { 1 8 } + \frac { 4 8 }{ 1 8 } \\
& = \frac { 4 2 + 2 1 + 4 8 } { 1 8 } \\
& = \frac { 1 1 1 } { 1 8 } \\
& = \frac { 3 7 } { 6 } \\
& = 6 \frac { 1 } { 6 }
\end {aligned} $$
جمعبندی
در این آموزش، با روش جمع کردن اعداد مخلوط برای حالتهای مختلف آشنا شدیم. دیدیم که با کمک شکل و محور اعداد میتوان جمع این اعداد را محاسبه کرد. همچنین، روشهای دیگری را همراه با حل مثال برای محاسبه مجموع دو عدد مخلوط بیان کردیم.










