توزیع های گسسته آماری و رابطه بین آنها — به زبان ساده
به منظور توصیف بسیاری از پدیدههای طبیعی از توزیعهای آماری استفاده میشود. بسیاری از این توزیعها براساس تعمیم یا حالت خاصی از یک توزیع اصلی بوجود آمدهاند. برای مثال پرتاب سکه و مشاهده خط یا شیر میتواند یک متغیر تصادفی با توزیع برنولی ایجاد کند که بیانگر مشاهده شیر یا غیر شیر در یکبار پرتاب سکه باشد. به همین ترتیب اگر این عمل تکرار شود و متغیر تصادفی $$X$$ نشانگر تعداد شیرهای مشاهده شده در $$n$$ بار پرتاب سکه باشد، خواهیم گفت که این متغیر تصادفی دارای توزیع دو جملهای است. پس به نظر میرسد که اگر تعداد پرتابها را n=1 در نظر بگیریم، توزیع برنولی حالت خاصی از توزیع دو جملهای خواهد بود. از طرفی ریشه اصلی برای ایجاد توزیع دو جملهای نیز متغیر تصادفی با توزیع برنولی بوده است. در این نوشتار به بررسی چنین روابطی خواهیم پرداخت تا توزیعهای آماری و رابطه بین آنها را بهتر بشناسیم. این گونه نوشتارها را در دو بخش ارائه خواهیم کرد. در بخش اول توزیع های گسسته آماری و رابطه بین آنها مورد بررسی قرار گرفته و در بخش دوم توزیع های پیوسته آماری و رابطه بین آنها مورد بحث قرار میگیرد.
در این متن به بررسی ارتباط بین چند توزیع گسسته خواهیم پرداخت. در دیگر نوشتارهای فرادرس با بسیاری از توابع توزیع آماری آشنا شدهایم. برای مشاهده لیستی از این گونه توابع میتوانید به نوشتار توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس مراجعه کنید. همچنین خواندن مطالب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیستند.
توزیع های گسسته آماری و رابطه بین آنها
توزیعهای احتمال، پایه و اساس آمار مدرن محسوب میشوند. بیان و توصیف بسیاری از پدیدههای تصادفی به کمک این توزیعها میسر است. برای کار با این توزیعها، ابزارهای مختلفی در زبانهای برنامهنویسی R و البته پایتون و کتابخانه scikit-learn وجود دارد. در این نوشتار به بررسی و معرفی بعضی از توابع که بخصوص در علم داده کاربرد بیشتری دارند پرداخته و رابطه یا نحوه تبدیل یکی به دیگری را مشخص خواهیم کرد.
هر توزیع آماری به کمک «تابع چگالی احتمال» (Probability Density Function) یا «تابع توزیع تجمعی» (Cumulative Probability Function) آن مشخص شده و معرفی میشود. به تابع چگالی احتمال به اختصار PDF و به تابع توزیع تجمعی احتمال نیز CDF گفته میشود. در ادامه به معرفی بعضی از «متغیرهای تصادفی» (Random Variable) و توزیعهای معروفشان میپردازیم. اگر مجموعه مقادیر متغیر تصادفی $$X$$ زیر مجموعهای از اعداد طبیعی یا به صورت یک مجموعه شمارشپذیر یا نامتناهی شمارشپذیر باشد، آن متغیر تصادفی را «گسسته» (Discreet Random Variable) مینامند. در این نوشتار به بررسی و معرفی ارتباط بین متغیرهای تصادفی گسسته و توزیعهایشان خواهیم پرداخت.
توزیع برنولی و یکنواخت
در یک بازی شانسی اگر برای بردن یا باختن دو وضعیت وجود داشته باشد، با یک آزمایش تصادفی برنولی مواجه هستیم. به این ترتیب اگر برای برنده شدن مقدار ۱ و برای باختن مقدار صفر را در نظر بگیریم، به این ترتیب متغیر تصادفی برنولی که نتیجه یک آزمایش برنولی است، دو مقدار ۰ و ۱ را خواهد داشت. احتمال موفقیت یا برابر بودن مقدار متغیر تصادفی با ۱ با $$p$$ و احتمال شکست نیز با $$1-p=q$$ نشان داده میشود. واضح است که به این ترتیب احتمال برابر بودن مقدار متغیر تصادفی با صفر برابر با $$q$$ خواهد بود.
در بازی پرتاب سکه، شانس یا احتمال مشاهده شیر (مقدار ۱) یا خط (صفر) برابر بوده در نتیجه مقدار $$p=0.5$$ خواهد بود ولی ممکن است در یک چنین بازی، سکه ناسالم بوده و احتمال مشاهده خط و شیر متفاوت باشد. ولی به هر حال برای توصیف چنین وضعیتی مثلا در بازی پرتاب دو تاس و مشاهده عددهای یکسان، توزیع برنولی (Bernoulli's Distribution) مناسب خواهد بود. در این حالت واضح است که احتمال موفقیت برابر با $$\frac{1}{6}$$ و احتمال شکست هم برابر با $$\frac{5}{6}$$ خواهد بود.
حال وضعیتی را در نظر بگیرید که برای یک مجموعه از پیشامدها شانس رخداد یکسان بوده و متناسب با تعداد آنها باشد. اگر هر یک از پیشامدها را با یک عدد نشان دهیم میتوانیم متغیر تصادفی $$X$$ را شماره مربوط به آن پیشامد در نظر بگیریم. برای مثال پرتاب یک تاس شش وجهی بیانگر چنین آزمایشی خواهد بود که احتمال مشاهده هر یک از وجهها ثابت و یکسان است. چنین وضعیتی منجر به تولید متغیر تصادفی با توزیع یکنواخت گسسته (Discreet Uniform Distribution) خواهد شد. به این ترتیب هر یک از ارقام روی وجهها دارای احتمال ثابت $$\frac{1}{6}$$ هستند.
توزیع دو جملهای و فوق هندسی
اگر یک آزمایش برنولی با پارامتر یا احتمال موفقیت ثابت $$p$$ را $$n$$ بار مستقلا تکرار کنیم، تعداد موفقیتها، یک متغیر تصادفی جدید با توزیع دوجملهای (Binomial Distribution) را میسازد. البته توجه دارید که در اینجا تعداد آزمایشها، ثابت و تعداد موفقیتها متغیر تصادفی را تشکیل میدهند.
اگر در هر بار تکرار آزمایش برنولی، شانس موفقت ثابت نباشد، متغیر تصادفی $$X$$ که بیانگر تعداد موفقیتها است دارای توزیع فوقهندسی (Hyper Geometric Distribution) خواهد بود. معمولا علت ثابت نبودن احتمال موفقیت در چنین وضعیتی، نمونهگیری بدون جایگزینی است.
توزیع پواسن

فرض کنید در یک آزمایش دو جملهای، احتمال موفقیت به تعداد آزمایشها وابسته باشد یعنی توزیع به شکل $$B(n,p_n)$$ باشد. به این ترتیب فرض بر این است که با بزرگ شدن $$n$$ مقدار احتمال موفقیت یا $$p_n$$ کوچک شود. به این معنی که احتمال موفقیت در یک بازه زمانی کوتاه یا فاصله مکانی کوچک، تقریبا صفر باشد. آنگاه میتوان گفت که تعداد موفقیتها دارای توزیع پواسن (Poisson Distribution) با پارامتر $$n\times p_n$$ است.
درست به مانند توزیع دو جملهای، توزیع پواسن نیز بیانگر تعداد موفقیتها است. با این تفاوت که پارامتر آن متوسط تعداد موفقیتها در یک واحد زمانی یا مکانی است. برای مثال تعداد مشتریانی که در یک زمان خاص به فروشگاه وارد میشوند یا تعداد تماسهای تلفنی در یک مقطع زمانی، از توزیع پواسن تبعیت میکنند و احتمال مشاهده مقدار خاصی برای این متغیر تصادفی متناسب با متوسط موفقیتها است.
توزیع هندسی و دو جملهای منفی
در توزیع دو جملهای، متغیر تصادفی همان تعداد موفقیتها در تکرار $$n$$ بار آزمایش برنولی با احتمال موفقیت ثابت و یکسان در نظر گرفته شد. اگر این امر برعکس شود یعنی با تکرار یک آزمایش برنولی، تعداد موفقیتها ثابت ولی تعداد آزمایشها برای رسیدن به اولین موفقیت متغیر تصادفی باشد، توزیع هندسی (Geometric Distribution) ایجاد خواهد شد. اهمیت این توزیع از آن جهت است که تعداد آزمایشهای لازم برای رسیدن به اولین موفقیت را مشخص میکند. برای مثال اگر میخواهید احتمال آنکه با تعداد بستههای ارسال شده مشخصی (مثلا ۱ Mb اطلاعات) در یک شبکه رایانهای، اولین برخورد (Collosion) در هاب رخ دهد باید از توزیع هندسی کمک بگیرید. البته از قبل میدانیم که متوسط رخداد چنین پیشامدی (تعداد برخوردها در هر مگابایت) چقدر است.
توزیع دوجملهای منفی (Negative Binomial) نیز ارتباط نزدیکی با آزمایش برنولی دارد. از این توزیع در بررسیهای پزشکی و صنعتی استفاده میشود. اگر متغیر تصادفی $$X$$، تعداد موفقیت در یک دنباله از آزمایشهای برنولی مستقل و هم توزیع (iid) پیش از $$r$$امین شکست یا موفقیت در نظر گرفته شود، میتوان توزیع احتمال $$X$$ را دو جملهای منفی در نظر گرفت. باز هم دیده میشود که آزمایش برنولی در این توزیعها نیز به کار گرفته شدهاند.
ارتباط بین توزیعهای گسسته
با توجه به رابطهای که بین متغیرهای تصادفی گسسته شرح داده شد، شاید نمایش ارتباط آنها توسط یک نمودار، کامل کننده بحث باشد. به تصویر زیر توجه کنید. متغیرهای تصادفی و یا توزیعهای مربوط به آنها در هر کادر مشخص شدهاند. جالب است که در این کادر، شکل یا نمودار توزیع متغیر تصادفی را هم مشاهده میکنید. خطوط جهتدار (فلش) بین توزیعها نیز ارتباط بین آنها را نشان میدهند. البته توجه داشته باشید که در بعضی از موارد ممکن است این خطوط دارای دو جهت باشند که نشان میدهد توزیعها قابل تبدیل به یکدیگر هستند.
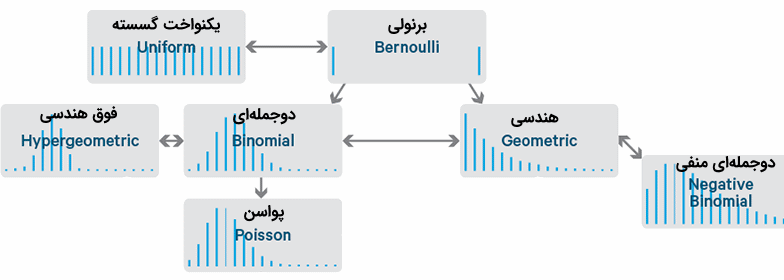
همانطور که دیده میشود بین توزیع برنولی و یکنواخت ارتباطی وجود دارد به این معنی که اگر به جای وضعیت دو تایی برای متغیر تصادفی، چند مقدار در نظر گرفته شود و شانس احتمال برای همه یکسان باشد، توزیع یکنواخت گسسته ایجاد میشود. از طرفی اگر توزیع یکنواخت را با متغیری دارای دو مقدار یا دو وضعیت در نظر بگیریم، به توزیع برنولی خواهیم رسید.
از سوی دیگر مجموع متغیرهای برنولی تبدیل به یک توزیع دوجملهای خواهد شد. اگر به جای مجموع موفقیتها، تعداد آزمایشهای برنولی در نظر گرفته شود، توزیع هندسی حاصل میشود. به همین دلیل بین توزیع برنولی با هر یک از توزیعهای دوجملهای و هندسی ارتباطی ترسیم شده است. البته بین توزیع هندسی و دوجملهای نیز اگر تعداد آزمایشها با تعداد موفقیتها جایگزین شود، ارتباطی وجود خواهد داشت.
برای توزیع دوجملهای منفی و توزیع هندسی نیز میتوان یک ارتباط در نظر گرفت. توزیع دوجملهای منفی تعداد آزمایشها برای رسیدن به $$r$$امین موفقیت بود. اگر در این توزیع تعداد موفقیتها $$r=1$$ باشد، توزیع هندسی حاصل خواهد شد. البته ذکر این نکته نیز ضروری است که احتمال موفقیت در توزیع هندسی در هر بار آزمایش ثابت و برابر با $$p$$ است.
اگر در توزیع دوجملهای، انتخابها (انتخاب مقدار مورد نظر موفقیت محسوب میشود) بدون جایگذاری باشند، توزیع فوقهندسی پدید خواهد آمد. از طرفی در آزمایش دوجملهای اگر احتمال رخداد موفقیت در هر بازه زمانی یا مکانی کوچک، ثابت و البته کوچک باشد و بستگی به بازه یا فاصله مکان داشته باشد، میتوانیم توزیع دوجملهای را به صورت پواسن در نظر بگیریم. گاهی از این خاصیت برای محاسبه احتمال متغیر تصادفی با توزیع دوجملهای توسط توزیع پواسن نیز بهره میبرند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار و احتمالات
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای نرمافزار آماری SPSS
- آزمایش تصادفی، پیشامد و تابع احتمال
- جامعه آماری — انواع داده و مقیاسهای آنها
- تحلیلها و آزمونهای آماری — مفاهیم و اصطلاحات
^^












درود. مطالبی که قرار می دهید واقعا راهگشاست. ممنون از زحمتی که می کشید.