تحلیل مش در مدار — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

قوانین مداری کیرشهف (KVL و KCL)، ابزار اساسی تحلیل هر مدار پیچیده‌ای را به ما می‌دهند، اما راه‌های دیگری مانند روش تحلیل جریان مش و روش تحلیل ولتاژ گره وجود دارند که ریاضیات و محاسبات تحلیل شبکه‌های بزرگ را کاهش می‌دهند.

مدار الکتریکی شکل زیر را در نظر بگیرید:

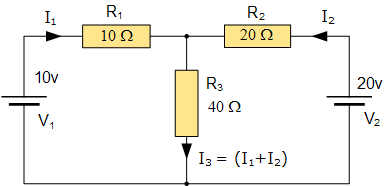
یک راه ساده برای کاهش محاسبات مربوط به تحلیل مدار، استفاده از معادلات قانون جریان کیرشهف برای تعیین جریان‌های $$I_1$$ و $$I_2$$ است. در این‌جا نیازی به محاسبه جریان $$I_3$$ مدار نیست، زیرا این جریان برابر با $$I_1+I_2$$ است. بنابراین، قانون ولتاژ کیرشهف، به نتیجه زیر می‌انجامد:

• معادله اول: $$10=50I_1+40I_2$$
• معادله دوم: $$20=40I_1+60I_2$$

در نتیجه، در نوشتن یک معادله اضافه صرفه‌جویی کردیم.

تحلیل جریان مش

یک راه ساده‌تر برای حل مدار بالا، استفاده ار تحلیل جریان مش (Mesh Current Analysis) یا تحلیل حلقه (Loop Analysis) است که گاهی روش جریان‌های گردشی ماکسول (Maxwell´s Circulating Currents) نیز نامیده می‌شود. در این روش، به جای نامگذاری جریان شاخه‌ها، جریان هر «حلقه بسته» را با جریان در حال گردش آن نامگذاری می‌کنیم.

فیلم آموزش مدارهای الکتریکی ۱ – مرور و حل تست در فرادرس

کلیک کنید

به عنوان یک قانون کلی، جهت جریان حلقه‌ها را موافق جهت حرکت عقربه‌های ساعت در نظر می‌گیریم. جریان هر شاخه را می توان با جریان‌های حلقه یا مش به دست آورد.

برای مثال: $$i_1=I_1$$، $$i_2=-I_2$$ و $$I_3=I_1-I_2$$.

اکنون، معادله قانون ولتاژ کیرشهف را می‌نویسیم که تضمین می‌کند معادلات به دست آمده از مدار، حداقل معادلاتی است که برای حل آن لازم است و می‌توان آن‌ها را به آسانی در یک فرم ماتریسی تعریف کرد.

مدار قبلی را در نظر بگیرید.

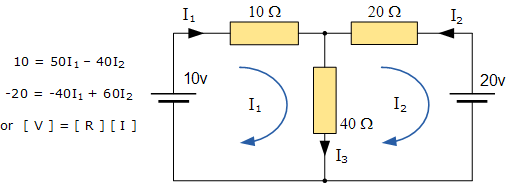
این معادلات را می‌توان به سرعت و توسط ماتریس امپدانس Z حل کرد. هر درایه قطر اصلی این ماتریس، مثبت است و امپدانس کل هر مش را نشان می‌دهد. در حالی که درایه‌های غیر از قطر اصلی، صفر یا منفی بوده و نشان دهنده امپدانس اجزایی از مدار است که بین مش‌ها مشترک هستند.

ابتدا باید به این نکته توجه کنیم که وقتی با ماتریس‌ها سر و کار داریم و می‌خواهیم یک ماتریس را بر ماتریس دیگر تقسیم کنیم، باید آن را در معکوس ماتریس ضرب نماییم. روابط زیر، این موضوع را نشان می‌دهند.

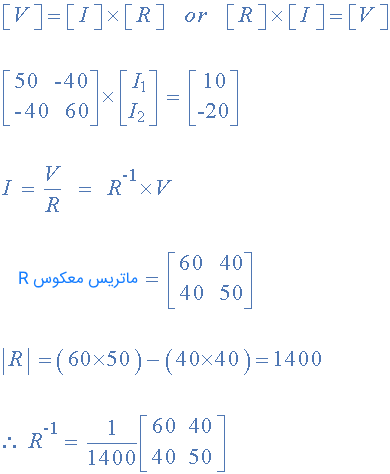
از آن‌جایی‌ که V/R معادل $$V\times R^{-1}$$ است و ماتریس معکوس R‌ را محاسبه کرده‌ایم، می‌توانیم دو جریان را به صورت زیر محاسبه کنیم:

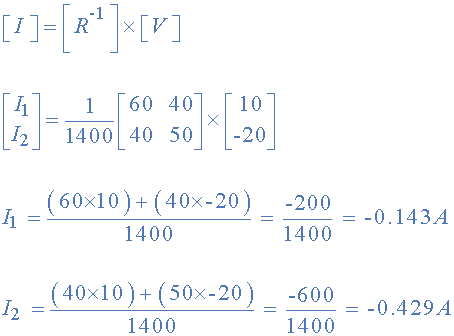
که در آن، [V] بردار منابع ولتاژ برای حلقه ۱ و حلقه 2، [I] بردار جریان حلقه‌هایی که در پی یافتن آن‌ها هستیم، [R] ماتریس مقاومت و [$$R^{-1}$$] معکوس ماتریس [R] است.

از آن‌جایی که $$I_3=I_1-I_2$$، مقدار $$I_3$$ نیز برابر با $$0.286$$ آمپر به دست می‌آید.

جمع‌بندی

شاید بتوان گفت که روش تحلیل مش، بهترین روش برای تحلیل مدار است. روند به کارگیری اصولی این روش، به صورت زیر است:

1. همه L حلقه‌ داخلی را با جریان‌های گردشی ($$I_1, I_2, ..., I_L$$)‌ نامگذاری کنید.
2. ماتریس برداری V‌ را با اندازه $$L\times 1$$  بنویسید که مجموع تمام منابع ولتاژ در هر حلقه است.
3. ماتریس با ابعاد $$L \times L$$‌ را با نام R برای تمام مقاومت‌های مدار به صورت زیر بنویسید:
   • $$R_{11}$$= مقاومت کل حلقه اول
   • $$R_{nn}$$= مقاومت کل حلقه Nاُم
   • $$R_{JK}$$= مقاومت مشترک حلقه J و حلقه K که منفی یا صفر است.
4. ماتریس یا بردار معادلات $$[V]=[R]\times[I]$$ را بنویسید که در آن، [I] جریان‌هایی است که باید محاسبه شوند.
5. جریان ها را با استفاده از معکوس ماتریس R محاسبه کنید.

مشابه تحلیل جریان مش، می‌توان از تحلیل ولتاژ گره نیز برای کاهش محاسبات قانون اهم استفاده کرد. در آموزش بعدی از نظریه مدارهای DC، تحلیل ولتاژ گره را معرفی خواهیم کرد.