بیوفارماسی در پایتون | بخش ۱: سیستم یک بخشی عروقی

در این مطلب یکی از مدلهای ساده و پرکاربرد برای توزیع داروهای تزریقی در خون را بررسی میکنیم که به آن سیستم یکبخشی عروقی گفته میشود.
مدل ریاضی توزیع دارو در خون
در شرایطی که دارو به صورت مستقیم وارد خون میشود و به صورت درجه یک از خون حذف میشود، به صورت زیر خواهیم داشت:
$$ {dC \over dt} = -K \times C$$
که در این رابطه، $$C$$ نشاندهنده غلظت پلاسمایی دارو $$t$$ نشاندهنده زمان و عدد $$K$$ نیز برابر با ثابت سرعت حذف دارو است.
با اندکی تغییر رابطه بالا به فرم زیر میرسیم:
$$ {dC \over C} = -K \cdot dt$$
حال میتوانیم از طرفین انتگرال بگیریم:
$$ \int {1 \over C} \cdot dC = \space - \int K \cdot dt $$
$$ {\ln \space C} = {\space \ln \space C_0} {-} {Kt} $$
حال میتوان مقدار $$C$$ را به شکل زیر به دست آورد:
$$ {\ln \space C} - {\ln \space C_0} = {- Kt} $$
$$ {\ln} {\large(} { {C} \over C_0} {\large) = -Kt} $$
$$ \frac{C}{C_{0}}=e^{-K t}$$
$$ C=C_{0} \cdot e^{-K t} $$
به این شکل مدل نهایی به دست آمد. حال میخواهیم یک مدلسازی روی دادههای واقعی انجام دهیم.
مدلسازی با دادههای واقعی در پایتون
فرض کنید 50 میلیگرم دارو به صورت تکدوز به بیماری تجویز شده است و غلظت پلاسمایی دارو در زمانهای مختلف در جدول زیر آورده شده است. با مدلسازی مناسب، ثابت سرعت حذف، سطح زیر نمودار تا بینهایت، نیمهعمر و کلیرانس را محاسبه کنید.
| Concentration (mg/L) | Time (h) |
| 1٫84 | ۰ |
| 1٫56 | ۰٫۵ |
| 1٫52 | ۱ |
| 1٫17 | ۲ |
| 0٫68 | ۴ |
| 0٫48 | ۶ |
| 0٫24 | ۸ |
| 0٫18 | ۱۰ |
ابتدا وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
1import math
2import numpy as np
3import scipy.optimize as opt
4import matplotlib.pyplot as pltاین کتابخانهها به ترتیب برای موارد زیر استفاده خواهند شد:
- محاسبات ریاضی
- کار با آرایه و محاسبات برداری
- بهینهسازی مدل
- رسم نمودار
حال تولید اعداد تصادفی را ثابت کرده و Style نمودارها را تنظیم میکنیم:
1np.random.seed(0)
2plt.style.use('ggplot')سطر اول باعث میشود در صورت استفاده از اعداد تصادفی در برنامه، در دفعات متفاوت از اجرای کد، نتایج یکسانی بگیریم و نتایج قابل بازتولید باشند. در سطر دوم نیز Style معروف ggplot استفاده شده است. حال دادهها را به صورت آرایه تعریف میکنیم:
1T = np.array([0, 0.5, 1, 2, 4, 6, 8, 10])
2C = np.array([1.84, 1.56, 1.52, 1.17, 0.68, 0.48, 0.24, 0.18])قبل از شروع، دادهها را مصورسازی میکنیم. برای این کار میتوانیم از Plot استفاده کنیم:
1plt.plot(T, C, lw=1.2, marker='o', ms=3, label='Plasma Concentration', c='crimson')
2plt.title('Data Visualization')
3plt.xlabel('Time (h)')
4plt.ylabel('Concentration (mg/L)')
5plt.axhline(c='k')
6plt.axvline(c='k')
7plt.legend()
8plt.show()بنابراین، در خروجی شکل زیر را داریم.
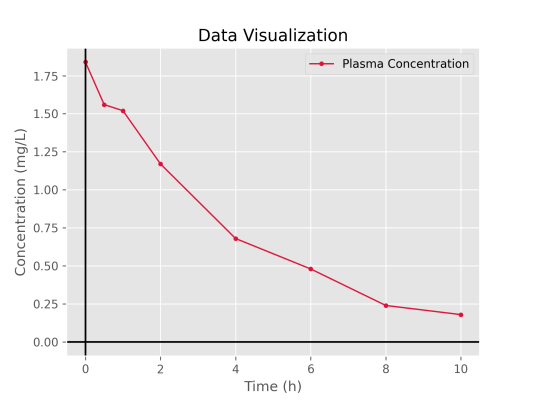
مشاهده میکنیم که نمودار حاصل، به نمودار تابع نمایی نزدیک است، بنابراین سیستم یکبخشی عروقی میتواند مورد استفاده قرار گیرد.
اکنون باید مدل را به صورت یک تابع تعریف کنیم. از آنجا که محاسبات برای مجموعهای از زمانها انجام میشود، باید تابع را متناسب با این نیاز بسازیم. این تابع در ورودی مقدار $$K$$، $$C_0$$ و زمانهای مورد نظر را خواهد گرفت و در خروجی غلظت در تک تک زمانهای ورودی را خواهد داد. بنابراین، خواهیم داشت:
1def Model (K:float, C0:float, T:np.ndarray):
2 C = C0 * np.exp( -K*T )
3 return Cتوجه داشته باشید که دو ورودی اول تابع اعدادی اعشاری هستند، ولی ورودی سوم یک بردار از نوع numpy.ndarray است. به دلیل اینکه در $$T$$ به جای یک عدد، با مجموعهای از اعداد کار میکنیم، باید از تابع numpy.exp به جای math.exp استفاده کنیم. خروجی این تابع نیز یک بردار از نوع numpy.ndarray است.
حالا میتوانیم با دادن $$K$$ و $$C_0$$ مناسب به تابع Model مقدار غلظت دارو در پلاسما را پیشبینی کنیم. ولی مقدار مناسب $$K$$ و $$C_0$$ معلوم نیست و باید آن را تعیین کنیم. برای این کار یک تابع خطا باید تعریف کنیم و آن را بهینه کنیم.
تابع خطا با گرفتن دادههای اصلی، $$K$$ و $$C_0$$ خواهد توانست خطای حاصل را برگرداند که یک عدد است. بنابراین داریم:
1def Error (Parameters:np.ndarray, T:np.ndarray, C:np.ndarray):
2 K = Parameters[0]
3 C0 = Parameters[1]
4 Prediction = Model(K, C0, T)
5 RMSE = np.mean( np.power(C – Prediction, 2) )**0.5
6 return RMSEنکتهای که باید به آن توجه کرد این است که $$K$$ و $$C_0$$ پارامترهای مدل هستند و باید به صورت یک آرایه با هم به تابع وارد شوند. بنابراین به صورت قراردادی، عضو اول Parameters را برابر با $$K$$ و عضو دوم آن را برابر با $$C_0$$ در نظر میگیریم.
در این تابع به ترتیب عملیات زیر را انجام میدهیم:
- مقدار $$K$$ را استخراج میکنیم.
- مقدار $$C_0$$ را استخراج میکنیم.
- با استفاده از تابع Model پیشبینی را انجام میدهیم.
- میانگین قدرمطلق خطاها را محاسبه میکنیم.
- به این خطا به اختصار RMSE گفته میشود که کوتاهشده عبارت Root Mean Squared Error است.
- توجه داشته باشید که چون $$Y$$ و Prediction آرایهای از اعداد هستند، باید از تابع numpy.power به جای pow استفاده کنیم.
- مقدار خطا را خروجی میگیریم.
به این صورت تابع خطا نیز تعریف میشود.
اکنون باید یک حدس اولیه از پارامترها داشته باشیم. با توجه به اینکه غلظت ثبت شده در زمان $$T=0$$ برابر با $$1.84$$است، احتمالاً همین عدد برای غلظت اولیه مناسب خواهد بود. برای ثابت سرعت حذف نیز میتوان عدد $$0.3$$ را محل شروع در نظر گرفت.
1Parameters0 = np.array([0.3, 1.84])حال میتوانیم بهینهسازی را انجام دهیم:
1Result = opt.minimize(Error, Parameters0, args=(T, C))این خط کد، تابع Error را با تغییر پارامترها بهینه میکند. با توجه به اینکه تابع خطا به جز پارامترها، دو آرایه دیگر مربوط به زمان و غلظت پلاسمایی را نیز در ورودی میگیرد، این دو مورد را در بخش args به صورت یک tuple تعریف میکنیم. خروجی این بخش کد یک دیکشنری با اسم Result خواهد بود که کمترین مقدار تابع، بهترین جواب، نتیجه بهینهسازی را در خود جای داده است.
از بین این موارد باید بهترین جواب را استخراج کنیم که با کلید 'x' در دسترس است. بنابراین میتوان نوشت:
1Parameters = Result['x']حال از روی Parameters میتوانیم مقدار $$K$$ و $$C_0$$ را استخراج کنیم:
1K = Parameters[0]
2C0 = Parameters[1]برای مشاهده مقادیر پارامترها نیز، اعداد را تا 4 رقم اعشار در خروجی نمایش میدهیم:
1print(f'K: {round(K, 4)} 1/h')
2print(f'C0: {round(C0, 4)} mg/L')پس از اجرا، نتایج زیر در خروجی ظاهر میشود.
K: 0.2352 1/h C0: 1.8359 mg/L
همانطور که انتظار داشتیم، مقدار $$C_ 0$$ عددی نزدیک به $$1.84$$ ظاهر شد.
حال میتوانیم کمترین مقدار خطا را نیز از Result استخراج کرده و نمایش دهیم:
1RMSE = Result['fun']
2print(f'RMSE: {round(RMSE, 4)} mg/L')پس از اجرا خواهیم داشت:
RMSE: 0.0426 mg/L
به این صورت مشاهده میکنیم که به خطای مناسبی دست یافتهایم. توجه داشته باشید که واحد خطای RMSE برابر با دادههای اصلی یعنی mg/L است.
حال میتوانیم سایر مقادیر خواسته شده را محاسبه کنیم:
سطح زیر نمودار تا بینهایت
برای به دست آوردن این مقدار، باید از رابطه اصلی به دست آمده انتگرال بگیریم:
$$\begin{aligned}
\int_{0}^{\infty} C \cdot d t=& \int_{0}^{\infty} C_{0} \cdot e^{-K t} \cdot d t=C_{0} \int_{0}^{\infty} e^{-K t} \cdot d t=C_{0}\left(\frac{e^{-\infty}}{-K}-\frac{e^{0}}{-K}\right) \\
&=C_{0}\left(\frac{0}{-K}-\frac{1}{-K}\right)=\frac{C_{0}}{K}
\end{aligned}$$
حال، با وارد کردن رابطه در برنامه داریم:
1AUC = C0/K
2print(f'AUC: {round(AUC, 4)} mg.h/L')که پس از اجرا به نتیجه زیر میرسیم:
AUC: 7.8035 mg.h/L
نیمه عمر
بر اساس تعریف، نیمه عمر برابر است با مدت زمانی که طول میکشد تا غلظت دارو نصف شود. بنابراین داریم:
$$ \begin{align*}
\frac{1}{2} C_{0} & =C_{0} \cdot e^{-K t_{h l}} \\ \Rightarrow 2^{-1}&=e^{-K t_{h l}} \\ \Rightarrow 2 &=e^{K t_{h l}} \\ \Rightarrow \ln 2 &=K t_{h l} \\ \Rightarrow t_{h l}
&=\frac{\ln 2}{K}
\end{align*} $$
حال خواهیم داشت:
1HL = math.log(2)/K
2print(f'HL: {round(HL, 4)} h')که در خروجی به این حالت داریم:
HL: 2.9482 h
این عدد با دادههای واقعی نیز سازگار است و میتوانیم روی نمودار به صورت تقریبی این نقطه را مشاهده کنیم.
کلیرانس
با توانایی بدن در پاکسازی حجم توزیع از دارو متناسب است و میتوان از فرمول زیر مقدار آن را به دست آورد:
$$C l=\frac{D}{A U C}$$
توجه داشته باشید که در این فرمول، $$D$$ مقدار داروی تزریقی است، پس خواهیم داشت:
1D = 50
2Cl = D/AUC
3print(f'Cl: {round(Cl, 4)} L/h')و در خروجی نیز نتیجه به این صورت خواهد بود:
Cl: 6.4074 L/h
حال میتوانیم نمودار حاصل از مدلسازی را با دادههای اصلی مقایسه کنیم. برای این کار ابتدا با استفاده از پارامترهای به دست آمده، پیشبینی انجام میدهیم:
1Prediction = Model(K, C0, T)اکنون میتوانیم دو نمودار را در کنار هم رسم کنیم:
1plt.plot(T, C, lw=1.3, marker='o', ms=3, label='Real', c='crimson')
2plt.plot(T, Prediction, lw=1.1,marker='x', ms=4, label='Predicted', c='teal')
3plt.title('Model Result')
4plt.xlabel('Time (h)')
5plt.ylabel('Concentration (mg/L)')
6plt.axhline(c='k')
7plt.axvline(c='k')
8plt.legend()
9plt.show()و در خروجی شکل زیر را داشته باشیم.
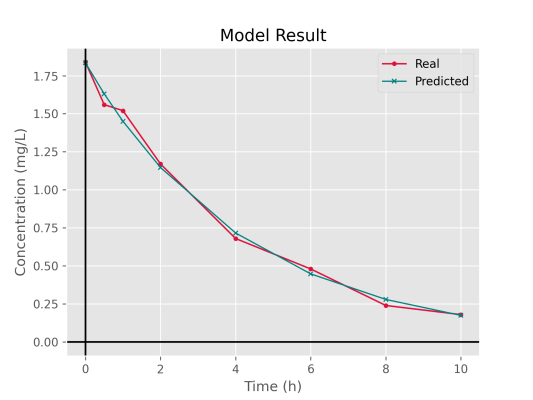
مشاهده میکنیم که مدل دقت خوبی از خود نشان داده است.
میتوان خطای مدل و رابطه نهایی را نیز وارد نمودار کرد و به این صورت نوشت:
1plt.plot(T, C, lw=1.3, marker='o', ms=3, label='Real', c='crimson')
2plt.plot(T, Prediction, lw=1.1,marker='x', ms=4, label='Predicted', c='teal')
3plt.text(2, 1.5, f'C = {round(C0, 4)} * exp(-{round(K, 4)} * t)')
4plt.text(4, 1.25, f'RMSE = {round(RMSE, 4)}')
5plt.title('Model Result')
6plt.xlabel('Time (h)')
7plt.ylabel('Concentration (mg/L)')
8plt.axhline(c='k')
9plt.axvline(c='k')
10plt.legend()
11plt.show()تا در خروجی شکل زیر را داشته باشیم.
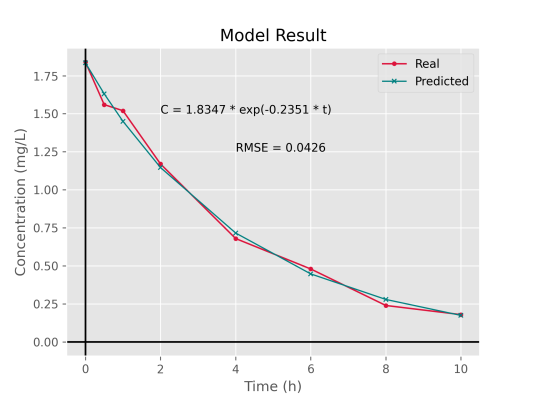
به این صورت میتوانیم نتیجه کار را به صورت جامع و کامل در یک نمودار نشان دهیم.
بهتر است در اینگونه مسائل، کمترین و بیشترین درصد خطا نیز آورده شود. برای این منظور، میتوانیم درصد قدرمطلق خطا (APE یا Absolute Percentage Error) را با استفاده از فرمول زیر محاسبه کنیم:
$$
A P E=100 \times\left|\frac{y-\hat{y}}{y}\right|
$$
درون کد میتوانیم با استفاده از numpy این بخش را پیادهسازی کنیم:
1APE = 100*np.abs( np.divide(C-Prediction, C) )و در نهایت کمترین، بیشترین و میانگین درصد قدرمطلق خطاها را بیابیم و در خروجی نمایش دهیم:
1MinAPE = np.min(APE)
2MeanAPE = np.mean(APE)
3MaxAPE = np.max(APE)
4
5print(f'Minimum APE: {round(MinAPE, 4)} %')
6print(f'Mean APE: {round(MeanAPE, 4)} %')
7print(f'Maximum APE: {round(MaxAPE, 4)} %')که خواهیم داشت:
Minimum APE: 0.2894 % Mean APE: 5.3739 % Maximum APE: 16.5446 %
جمعبندی
در این مطلب یاد گرفتیم که مدل یکبخشی عروقی را روی دادههای واقعی برازش (Fit) کنیم، پارامترهای مورد نیاز را محاسبه و مدل را ارزیابی کنیم.
نتایج را به صورت نمودار مشاهده کنیم. مدل ارائهشده حالت سادهای از سیستم و ارتباط موجود بین دارو و بدن است. در مطالب بعدی به مدلهای برای مدلسازی شرایط پیچیدهتر خواهیم پرداخت.










