بسط ضمنی (Implicit Expansion) در متلب — راهنمای جامع

عبارت بسط ضمنی (Implicit Expansion) یا Broadcasting در نرم‌افزار متلب، در واقع نحوه رفتار نرم‌افزار با آرایه‌های دارای ابعاد متفاوت را هنگام انجام عملیات ریاضی مشخص می‌کند. در این نوشتار قصد داریم به بررسی این قابلیت در نرم‌افزار متلب بپردازیم. قابلیت بسط ضمنی در نسخه‌های اخیر نرم‌افزار متلب به آن افزوده شده است. این قابلیت در زبان پایتون نیز روی آرایه‌هایی که توسط پکیج NumPy ایجاد می‌شوند، قابل پیاده‌سازی است.

بسط در نرم‌افزار متلب

فرض کنید که در یک قطعه کد پردازش تصویر، لازم باشد ستون‌های ماتریسی به نام RGB با ابعاد $$P \times 3$$ را در المان‌های متناظر از بردار v با ابعاد $$1 \times 3$$ ضرب کنیم. در واقع ماتریس RGB شامل p رنگ (یک رنگ در هر ردیف) است.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

برای این کار در نسخه‌های قدیمی باید به صورت زیر عمل می‌کردیم.

1RGB_c = [RGB(:,1)*v(1)  RGB(:,2)*v(2)  RGB(:,3)*v(3)];

اما در نسخه‌های جدیدتر از نرم‌افزار متلب، دیگر لازم نیست از کد بالا استفاده کرد. بلکه می‌توان قطعه کد زیر را به جای آن برای محاسبه به کار برد.

1RGB_c = RGB .* v;

استفاده از این دستور در نسخه‌های قدیمی‌تر از متلب 2016 موجب ایجاد خطای زیر می‌شود.

>> RGB_c = RGB .* v
Error using  .* 
Matrix dimensions must agree.

اما در نسخه‌های جدید، نرم‌افزار متلب بردار v را به صورت ضمنی (Implicitly) بسط می‌دهد تا سایز آن با سایز ماتریس RGB برابر شود و در نتیجه بتوان از ضرب المان در المان (Elementwise) استفاده کرد. توجه کنید دلیل استفاده از عبارت بسط ضمنی این است که نرم‌افزار متلب واقعا یک کپی در حافظه (In-memory) از بردار بسط داده شده را ایجاد نمی‌کند.

تفریق میانگین ستون‌ها

برای روشن‌تر شدن بحث، در ادامه مثال دیگری را مطرح می‌کنیم. ماتریس اعداد تصادفی A را با استفاده از دستور زیر در متلب ایجاد می‌کنیم.

1A = rand(3,3)

ماتریس به شکل زیر خواهد بود.

A =
      0.48976      0.70936       0.6797
      0.44559      0.75469       0.6551
      0.64631      0.27603      0.16261

حال فرض کنید که می‌خواهیم هر ستون از این ماتریس A را اصلاح کنیم و برای این کار، باید مقدار میانگین هر ستون را از المان‌های آن ستون کم کنیم. استفاده از دستور mean در متلب این امکان را فراهم می‌کند که مقدار میانگین داده‌های ستون‌های یک ماتریس را محاسبه کرد.

1ma = mean(A)

مقدار میانگین هر ستون از ماتریس A برابر است با:

ma =
      0.52722      0.58003      0.49914

اما به این دلیل که بردار ma دارای سایز یکسان با ماتریس A و یک اسکالر نیست، نمی‌توانید ma را مستقیما از ماتریس A کم کنید. در نتیجه باید ابتدا ma را به اندازه ماتریس A بسط داد و سپس آن را از ماتریس A کم کرد.

در نسل اول متلب، برنامه‌نویسان از یک تکنیک اندیس‌دهی برای بسط استفاده می‌کردند که Tony's Trick نام داشت. این تکنیک به صورت زیر بود.

1ma_expanded = ma(ones(3,1),:)

ماتریس حاصل از اجرای دستور فوق به صورت زیر است.

ma_expanded =
      0.52722      0.58003      0.49914
      0.52722      0.58003      0.49914
      0.52722      0.58003      0.49914

حال می‌توان عمل تفرق را انجام داد.

1A - ma_expanded

نتیجه به صورت زیر به دست می‌آید.

ans =
    -0.037457      0.12934      0.18057
    -0.081635      0.17466      0.15596
      0.11909       -0.304     -0.33653

در نسل دوم متلب، بسیاری از برنامه‌نویسان برای بسط، از تابعی به نام repmat استفاده می‌کردند که مخفف Replicate Matrix بود. نحوه استفاده از این تابع به صورت زیر است.

1ma_expansion = repmat(ma,3,1)

نتیجه حاصل از این دستور، به صورت زیر به دست می‌آید.

ma_expansion =
      0.52722      0.58003      0.49914
      0.52722      0.58003      0.49914
      0.52722      0.58003      0.49914

استفاده از تابع repmat در بهبود کد نسبت به روش Tony's Trick تاثیر داشت، اما مشکلی که پیش می‌آمد این بود که نرم‌افزار ماتریس بسط داده شده را هنوز هم در حافظه ایجاد می‌کرد. برای مسائل بسیار بزرگ، اختصاص حافظه اضافه و نیز کپی کردن در حافظه، باعث کاهش چشمگیر سرعت محاسبات و یا حتی خطای عدم وجود حافظه می‌شود.

بنابراین در نسل سوم متلب، تابع جدیدی به نام bsxfun ایجاد شد که این قابلیت را داشت تا عمل تفریق را مستقیما بدون بسط بردار در حافظه انجام دهد. برای فراخوانی این تابع باید به صورت زیر عمل کرد.

1bsxfun(@minus,A,ma)

نتیجه حاصل از این تابع به صورت زیر است.

ans =
    -0.037457      0.12934      0.18057
    -0.081635      0.17466      0.15596
      0.11909       -0.304     -0.33653

سه حرف bsx در نام تابع، حروف اختصاری Binary Singleton Expansion هستند که Binary در این عبارت به عملگرهایی اشاره می‌کند که دو ورودی را دریافت می‌کنند. تابع bsxfun مورد استفاده کاربران قرار گرفت و در یک سال ۱۸۰۰ بار در ۷۴۰ فایل از آن استفاده شد. اما این تابع مشکلاتی داشت.

مشکلات تابع bsxfun

تابع bsxfun دارای مشکلات عملکردی زیر بود:

فیلم آموزش برنامه نویسی متلب پیشرفته در فرادرس

کلیک کنید

• تعداد زیادی از کاربران از وجود این تابع خبر نداشتند، زیرا اکثر آن‌ها هنگام انجام عمل تفریق با جست‌و‌جو در help متلب به این تابع پی نمی‌بردند.
• استفاده از تابع bsxfun نیاز به داشتن یک سطح از مفهوم برنامه‌نویسی (فراخوانی یک تابع برای اعمال یک تابع دیگر روی یک مجموعه از ورودی‌ها) داشت که با کاربرد این تابع (در ریاضیات پایه) همخوانی نداشت.
• استفاده از تابع bsxfun نیاز به داشتن دانش نسبتا بالایی از برنامه‌نویسی متلب داشت. کاربر باید با مدیریت تابع (Function Handles) و همچنین توابع معادل با عملگرهای ریاضی در متلب مانند plus و minus و times و rdivide آشنا بود.
• کدهایی که از این تابع استفاده می‌کردند، دارای ظاهری شبیه به کدهای ریاضی نبودند.
• تولید کدهایی که به اندازه کدهای ریاضی پایه موثر باشند برای موتور اجرایی نرم‌افزار متلب دشوار بود.

به این دلایل، عملگر‌های ریاضی دو ورودی (Two-Input Arithmetic Operators)، عملگرهای منطقی (Logical Operators) و عملگرهای نسبی (Relational Operators) و بسیاری توابع دو ورودی در متلب دچار تغییر شدند تا مانند bsxfun، در صورت وجود اندازه‌های سازگار (Compatible Sizes) عمل بسط به صورت اتوماتیک انجام یابد.

اندازه‌های سازگار

دستور A - B تا زمانی عمل می‌کند که A و B دارای اندازه‌های سازگار باشند. دو آرایه دارای اندازه سازگار هستند اگر برای هر بعد، اندازه‌ بعد ورودی‌ها یا یکسان باشند و یا یکی از آن‌ها یک باشد. در موارد ساده‌تر، اندازه‌های دو آرایه زمانی سازگار هستند که دقیقا با یکدیگر یکسان باشند و یا یکی از آن‌ها یک اسکالر باشد. در زیر، چند مثال از اندازه‌های سازگار را در حالات مختلف بیان می‌کنیم.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

• دو ورودی که دارای اندازه دقیقا یکسان هستند.

• یکی از ورودی‌ها، اسکالر است.

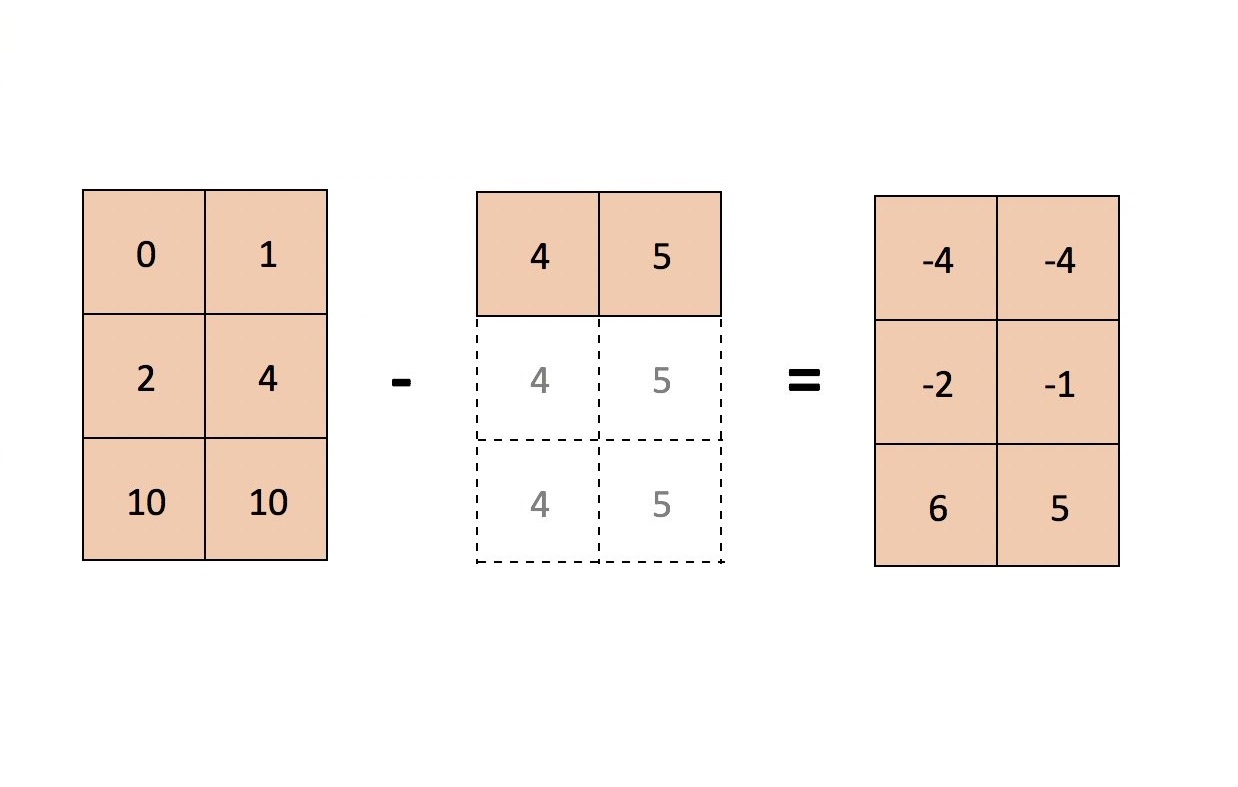
• یکی از ورودی‌ها، یک ماتریس است و ورودی دیگر، یک بردار ستونی با تعداد سطرهای برابر با سطرهای ماتریس است. همچنین این امکان وجود دارد که بردار سطری باشد و تعداد ستون‌های بردار و تعداد ستون‌های ماتریس با یکدیگر برابر باشند.

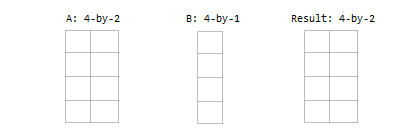
• یکی از ورودی‌ها، برداری ستونی است و ورودی دیگر، یک بردار سطری است. توجه کنید که در این حالت هر دو ورودی بسط می‌یابند اما جهت بسط هر کدام متفاوت خواهد بود.

• یکی از ورودی‌ها یک ماتریس است و ورودی دیگر، یک آرایه سه بعدی است که تعداد سطرها و ستون‌های آرایه سه بعدی با تعداد سطرها و ستون‌های ماتریس برابر هستند. توجه کنید که در این حالت، اندازه ماتریس A در بعد سوم به صورت ضمنی برابر با یک در نظر گرفته می‌شود و بنابراین می‌توان ماتریس A را در بعد سوم گسترش داد تا با اندازه B برابر شود.

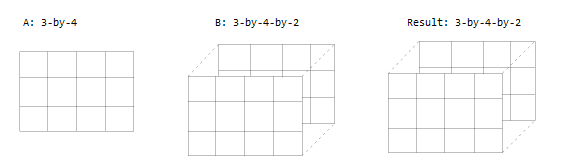
• یکی از ورودی‌ها یک ماتریس و ورودی دیگر یک آرایه سه بعدی است. ابعاد یا همگی با هم برابر هستند و یا در غیر این صورت، یکی از آن‌ها ۱ است. توجه کنید که این یکی دیگر از حالت‌هایی است که هر دو ورودی به صورت ضمنی بسط می‌یابند.

توابع و عملگرهای مشمول بسط ضمنی در متلب

در زیر لیستی از توابع و عملگرهایی را می‌توان دید که بسط ضمنی متلب شامل آن‌ها می‌شود.

+       -       .*      ./
.\      .^      <       <=
>       >=      ==      ~=
|       &
xor     bitor   bitand  bitxor
min     max     mod     rem
hypot   atan2

این امکان وجود دارد که با گذشت زمان، توابع دیگری نیز به این لیست افزوده شود.

ایرادهای بسط ضمنی

افزوده شدن قابلیت بسط ضمنی به متلب، موجب بحث‌ها و نگرانی‌هایی در بین برنامه‌نویسان و کاربران این نرم‌افزار شد. برخی از آنان نگران بودند که ممکن است یک کاربر کدی را نوشته باشد که بسته به این توابع و عملگرها، یک پیام خطا تولید شود. در حالی که پس از ارزیابی کدها و برنامه‌های آزمایشی در نسخه‌های مختلف، هیچ مشکل ناساگاری در عمل دیده نشد.

برخی دیگر از کاربران بر این عقیده بودند که رفتار عملگرهای جدید دقیقا مبتنی بر نحوه نوشتن یا نوتیشن (Notation) جبر خطی نیست. با این حال، بهتر است نرم‌افزار متلب را یک نوتیشن جبر خطی محض در نظر نگیریم، بلکه دقیق‌تر این است که متلب را یک نوتیشن محاسباتی آرایه‌ها و ماتریس‌ها به حساب بیاوریم. با این شرط، می‌توان متلب را دارای سابقه طولانی در ابداع نوتیشن‌هایی دانست که امروزه به صورت وسیع پذیرفته شده‌اند و مورد استفاده قرار می‌گیرند. از جمله این نوتیشن‌ها می‌توان به Backslash و دو نقطه (Colon) و انواع مختلف زیرنویس‌ها (subscripting) اشاره کرد.

در نهایت، عده دیگری از کاربران نگران این امر بودند که ممکن است یک کاربر مثلا هنگام جمع دو بردار، متوجه نباشد که یکی از آن‌ها ستونی و دیگری سطری است و جایی در داخل برنامه این عمل انجام گرفته باشد. در نسخه‌های قدیمی متلب، جمع این دو بردار موجب ایجاد یک خطا در برنامه می‌شد. اما با افزوده شدن خاصیت بسط ضمنی، جمع این دو بردار موجب ایجاد یک ماتریس (به این ماتریس جمع بیرونی می‌گویند) می‌شود.

اما در پاسخ باید گفت که پی بردن به این خطا و رفع آن بسیار ساده است و نیاز به زمان زیادی ندارد. می‌توان گفت پی بردن به این خطا حتی سریع‌تر از پی بردن به خطای استفاده اشتباه از عملگر * به جای عملگر *. است. همچنین محدودیت جدید متلب روی سایز آرایه‌ها نیز از ایجاد ماتریس‌های با ابعاد بسیار بزرگ جلوگیری می‌کند تا موجب به وجود آمدن شرایط عدم حافظه نشود.

مثال‌هایی از کاربرد بسط ضمنی در متلب

در این قسمت می‌خواهیم به بررسی چند مثال بپردازیم که نحوه استفاده کاربران متلب از دستور bsxfun را نشان می‌دهد. این مثال‌ها از متداول‌ترین کاربردهای bsxfun هستند. پس از نوشتن هر برنامه با استفاده از تابع bsxfun، نحوه نوشتن آن قطعه کد در نسخه‌های جدید متلب با قابلیت بسط ضمنی نیز نشان داده شده است.

فیلم آموزش پردازش تصویر در متلب در فرادرس

کلیک کنید

اعمال یک ماسک روی تصویر رنگی

% mask: 480x640
% rgb:  480x640x3

1% OLD
2rgb2 = bsxfun(@times,rgb,mask);

1% NEW
2rgb2 = rgb .* mask;

نرمالیزه کردن ستون‌های یک ماتریس (کم کردن میانگین و تقسیم بر انحراف معیار)

در این برنامه ابتدا در یک ماتریس میانگین هر ستون را از آن کم می‌کنیم و سپس آن را بر انحراف معیار تقسیم می‌کنیم.

1% X: 1000x4
2mu = mean(X);
3sigma = std(X);

1% OLD
2Y = bsxfun(@rdivide,bsxfun(@minus,X,mu),sigma);

1% NEW
2Y = (X - mu) ./ sigma;

محاسبه ماتریس فاصله

برای دو مجموعه از بردارها، فاصله اقلیدسی بین هر زوج بردار را می‌توان به روش زیر محاسبه کرد.

1% X: 4x2 (4 vectors)
2% Y: 3x2 (3 vectors)
3X = reshape(X,[4 1 2]);
4Y = reshape(Y,[1 3 2]);

1% OLD
2m = bsxfun(@minus,X,Y);
3D = hypot(m(:,:,1),m(:,:,2));

1% NEW
2m = X - Y;
3D = hypot(m(:,:,1),m(:,:,2));

محاسبه جمع بیرونی

این مثال از پیاده‌سازی تابع toeplitz گرفته شده است.

1cidx = (0:m-1)';
2ridx = p:-1:1;

1% OLD
2ij = bsxfun(@plus,cidx,ridx);

1% NEW
2ij = cidx + ridx;

یافتن اعداد صحیح (Integers) که مضربی از یکدیگر هستند

این مثال از محاسبه ماتریس Redheffer در تابع gallery گرفته شده است و رفتار بسط ضمنی را در یک تابع نشان می‌دهد.

1i = 1:n;

1% OLD
2A = bsxfun(@rem,i,i') == 0;

1% NEW
2A = rem(i,i') == 0;

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌ های برنامه‌‌ نویسی
• مجموعه آموزش های برنامه‌نویسی متلب (MATLAB)
• مجموعه آموزش‌های پروژه محور برنامه‌نویسی
• مجموعه آموزش های برنامه‌نویسی متلب برای علوم و مهندسی
• منابع آموزشی نرم افزار متلب و برنامه نویسی کاربردی با آن
• تقلب نامه (Cheat Sheet) توابع و دستورات متلب (MATLAB)
• تقلب نامه (Cheat Sheet) تولباکس بهینه سازی در متلب — راهنمای کاربردی

^^