برنامه نویسی پویا در علم داده | راهنمای کاربردی

در این مطلب، مفاهیم برنامه نویسی پویا در علم داده مورد بررسی قرار گرفته و این مبحث همراه با مثال‌هایی که درک آن‌ها آسان باشد شرح داده شده است.

برنامه نویسی پویا در علم داده

الگوریتم‌ها و ساختارهای داده، بخش جدایی ناپذیری از «علم داده» (Data Science) هستند. با وجود آنکه اغلب «دانشمندان داده» (Data Scientists) در طول مطالعات خود، دوره‌های تحلیل و طراحی الگوریتم مناسبی را نمی‌گذارند، اما این مبحث بسیار حائز اهمیت است و دانشمندان داده نیز نیازمند آن هستند که با مبحث ساختار داده و طراحی الگوریتم آشنایی کامل و جامع داشته باشند. شایان توجه است که بسیاری از شرکت‌ها، طی فرایند مصاحبه شغلی برای استخدام دانشمند داده، پرسش‌هایی پیرامون «طراحی الگوریتم» (Algorithm Design) و «ساختمان داده» (Data Structure) نیز مطرح می‌کنند. اکنون، پرسشی که افراد زیادی با آن مواجه می‌شوند این است که اهمیت پرسیدن سئوالاتی پیرامون ساختمان داده از متقاضیان استخدام به عنوان دانشمند داده چیست. در پاسخ به این پرسش در ساده‌ترین حالت می‌توان گفت، جوابی که فرد به این پرسش می‌دهد، می‌تواند به نوعی سطح دانش برنامه‌نویسی او را نشان دهد. بنابراین، توصیه می‌شود که علاقه‌مندان به اشتغال در مشاغل حوزه علم داده، مطالعاتی نیز پیرامون ساختمان داده و طراحی الگوریتم داشته باشند.

برنامه نویسی پویا در علم داده چطور کار می‌کند؟

فرض می‌شود که قرار است nامین عدد فیبوناچی پیدا شود. سری فیبوناچی یک دنباله از اعداد است که در آن، هر عدد (عدد فیبوناچی) مجموعه دو عدد ماقبل خودش است. آغاز سری فیبوناچی به صورت زیر است:

1, 1, 2, 3, 5, 8

برنامه محاسبه سری فیبوناچی در ادامه آمده است.

def fib(n):
    if n<=1:
        return 1
    return fib(n-1) + fib(n-2)

کد ارائه شده در بالا برای ارائه اعداد فیبوناچی، به صورت بازگشتی است. اما مشکلی در روش ارائه شده در بالا وجود دارد. اگر فرد تلاش کند که fib(n=7)‎ را محاسبه کند، باید fib(5)‎ را دو بار، fib(4)‎ سه بار و fib(3)‎ را پنج بار اجرا کند. هر چه n بزرگ‌تر می‌شود، فراخوانی‌های زیادتری برای اعداد مشابه انجام می‌شود و تابع بازگشتی آن را بارها و بارها محاسبه می‌شود.

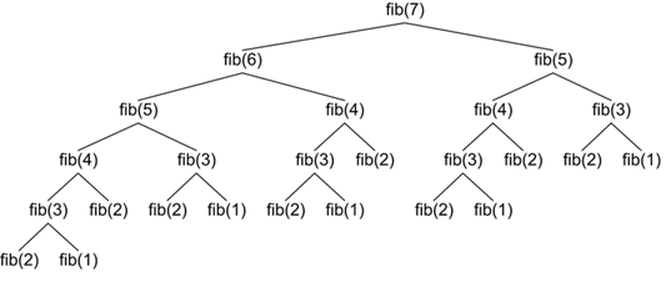
در حال حاضر، بازگشت یک رویکرد بالا به پایین است. همچون هنگامی که عدد فیبوناچی n محاسبه می‌شود، کار از n آغاز می‌شود و سپس، فراخوانی بازگشتی برای n-2 و n-1 و به همین صورت، انجام می‌شود. در برنامه‌نویسی پویا، یک رویکرد پایین به بالا اتخاذ می‌شود. این راهکاری برای انجام بازگشت‌ها به صورت تکرار شونده است. کار با محاسبه fib(0)‎ و fib(1)‎ آغاز می‌شود و سپس، با استفاده از نتایج قبلی، نتایج جدید تولید می‌شوند.

def fib_dp(n):
    dp_sols = {0:1,1:1}
    for i in range(2,n+1):
        dp_sols[i] = dp_sols[i-1] + dp_sols[i-2] 
    return dp_sols[n]

چرا برنامه نویسی پویا در علم داده دشوار است؟

بازگشت، یک مفهوم ریاضیاتی است. در حل مسائل، معمولا سعی می‌شود که راهکار مساله بزرگ‌تر، با شکستن آن به مسائل کوچک‌تر پیدا شود. برنامه‌نویسی پویا بر ایده مشابهی استوار است، اما در برنامه‌نویسی پویا، همه زیرمسائل از پیش محاسبه می‌شوند که ممکن است نیاز به محاسبه به صورت پایین به بالا داشته باشند.

انسان‌ها، معمولا به صورت سخت کوشانه‌ای سعی دارند که به روش بالا به پایین کار کنند. این همان شیوه یادگیری است که افراد سعی می‌کنند هر چیز را پیش از مطالعه به صورت عمقی، به صورت سطحی مطالعه کنند. خب؛ چطور می‌توان به شیوه پایین به بالا فکر کرد؟ در ادامه، برای درک بهتر مفهوم برنامه‌نویسی پویا، مساله‌ای ارائه شده است که با استفاده از برنامه‌نویسی پویا حل خواهد شد. ایده کلی این است که در صورت دانستن راهکار زیرمسائل کوچک، می‌توان مسئله بزرگ‌تر را حل کرد.

• برای دیدن فیلم آموزش کامل برنامه نویسی پایتون (Python) + اینجا کلیک کنید.

مثالی از برنامه نویسی پویا در علم داده

یک مسیر شبکه‌ای m x n که با طلا پر شده، ارائه شده است. هدف پیدا کردن مسیری از بالا چپ به پایین راست است که مجموعه طلا را در امتداد مسیر بیشینه کند. تنها می‌توان با آغاز از (0,0) به پایین یا راست حرکت کرد. اکنون می‌توان مسیرهای زیادی را انتخاب کرد. می‌توان به انتهای راست مسیر و سپس پایین رفت و یا می‌توان یک مسیر زیگ‌زاگ را انتخاب کرد؟

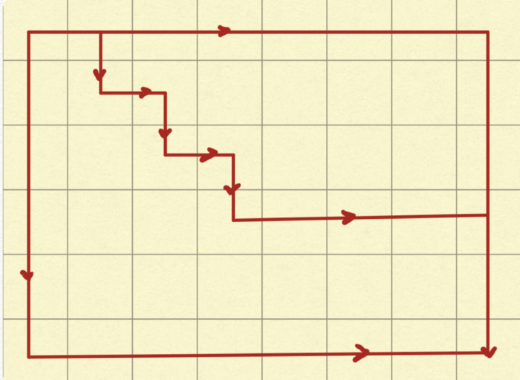
اما تنها یک/تعداد کمی مسیر هستند که موجب پولدار شدن فرد می‌شوند. اما چطور حتی می‌توان به چنین مسئله‌ای فکر کرد؟ هنگامی که به پرسش‌های برنامه‌نویسی خطی فکر می‌شود، یک رویکرد پایین به بالا اتخاذ می‌شود. در این مثال، ساده‌ترین مسئله برای حل کردن، حالت پایه‌ای است. حداکثر میزان طلایی که می‌توان با رسیدن به سلول (۰،۰) به دست آورد، چند است؟ پاسخ، بسیار ساده است. این مقدار، همان مقدار خود سلول است.

پس از حل مسئله ساده بالا، مسائل پیچیده‌تر مورد بررسی قرار می‌گیرند.

میزان طلایی که با رفتن به سلول‌های (0,1) و (1,0) حاصل می‌شود چقدر است. این موارد نیز بسیار ساده هستند. می‌توان به (0,1) و (1,0) تنها از طریق (0,0) رفت و از این رو، بیشینه طلایی که می‌توان به دست آورد مقدار موجود در سلول (0,1)/(1,0) به علاوه بیشینه طلایی است که هنگام رسیدن به سلول (0,0) می‌توان به دست آورد.

اما درباره سلول (0,2) چه می‌توان گفت؟ مجددا، تنها یک مسیر. بنابراین اگر راه حل به (0,1) مشخص است، می‌توان فقط مقدار سلول (0,2) را برای به دست آوردن راهکار برای (0,2) محاسبه کرد. اکنون، کار مشابهی برای یک سلول دلخواه انجام می‌شود. هدف، استخراج رابطه در اینجا است.

بنابراین، در مورد یک سلول دلخواه، می‌توان از بالا یا سمت راست به آن رسید. اگر راهکار رو به بالا و به سمت چپ مشخص است، می‌توان راهکار را برای سلول دلخواه کنونی محاسبه کرد.

کدنویسی و برنامه نویسی پویا در علم داده

هنگامی که بینش اصلی حاصل شد، کدنویسی برای آن بسیار ساده است. کار با محاسبه راهکار برای اولین سطر و اولین ستون آغاز می‌شود. سپس، کار برای محاسبه مقادیر دیگر در شبکه با استفاده از روابطی که پیش از این به دست آمده است، انجام می‌شود.

def maxPathSum(grid):
    m = len(grid)
    n = len(grid[0])
    # sol keeps the solutions for each point in the grid.
    sol = list(grid)
    # we start by calculating solutions for the first row
    for i in range(1,n):
        sol[0][i] += sol[0][i-1]
    # we then calculate solutions for the first column
    for i in range(1,m):
        sol[i][0] += sol[i-1][0]
    # we then calculate all the solutions in the grid
    for i in range(1,m):
        for j in range(1,n):
            sol[i][j] += max(sol[i-1][j],sol[i][j-1])
    # return the last element
    return sol[-1][-1]

جمع‌بندی

برنامه‌نویسی پویا، مبنای برخی از متداول‌ترین پرسش‌ها در مصاحبه‌های استخدامی یادگیری ماشین و علم داده را شکل می‌دهد و به دست آوردن درک خوبی در این رابطه، می‌تواند به فرد در اینکه شغل مورد نظر خود را به دست آورد کمک قابل توجهی کند.