برنامه محاسبه nامین عدد فیبوناچی — به زبان ساده

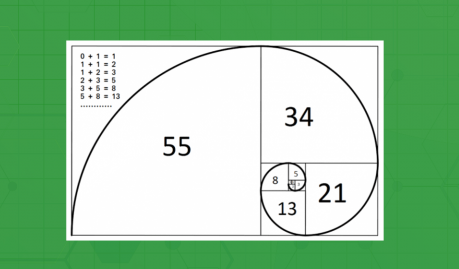
در این مطلب، روش‌های گوناگون نوشتن برنامه محاسبه nامین عدد فیبوناچی مورد بررسی قرار گرفته و سپس، پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و «پی‌اچ‌پی» (PHP) انجام شده است. اعداد فیبوناچی، اعدادی هستند که در توالی اعداد صحیح زیر قرار داشته باشند.

۰, ۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, …

به بیان ریاضی، توالی F_n از اعداد فیبوناچی با استفاده از رابطه بازگشتی زیر، تعریف شده است.

F_n = F_n-1 + F_n-2

در رابطه بالا، مقدار دانه برای F₀ = 0 و برای F₁ = 1 است.

F₀ = 0 and F₁ = 1

فرض می‌شود عدد n داده شده است. هدف، نوشتن برنامه‌ای است که n‌اُمین عدد فیبوناچی را چاپ کند. مثال‌های زیر در این راستا قابل توجه هستند.

Input: n = ۲

Output: ۱



Input: n = ۱

Output: ۳۴

در ادامه، تابع (int fib(int n نوشته می‌شود که مقدار F_n را باز می‌گرداند. برای مثال، اگر n = 0 باشد، ()fib باید ۰ و اگر n = 1 باشد، تابع ()fib باید مقدار ۱ را بازگرداند. برای n > 1، باید مقدار F_n-1 + F_n-2 بازگردانده شود.

For n = 9

Output: ۳۴

در ادامه، روش‌های گوناگون محاسبه nامین عدد فیبوناچی ارائه شده است.

روش اول محاسبه nامین عدد فیبوناچی

یک راهکار ساده برای محاسبه nامین عدد فیبوناچی، پیاده‌سازی مستقیم رابطه ریاضی بازگشتی است که پیش‌تر ارائه شد.

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در ++C

//Fibonacci Series using Recursion 
#include<bits/stdc++.h> 
using namespace std; 
  
int fib(int n) 
{ 
    if (n <= 1) 
        return n; 
    return fib(n-1) + fib(n-2); 
} 
  
int main () 
{ 
    int n = 9; 
    cout << fib(n); 
    getchar(); 
    return 0; 
} 
  
// This code is contributed 
// by Akanksha Rai 

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در C

//Fibonacci Series using Recursion 
#include<stdio.h> 
int fib(int n) 
{ 
   if (n <= 1) 
      return n; 
   return fib(n-1) + fib(n-2); 
} 
  
int main () 
{ 
  int n = 9; 
  printf("%d", fib(n)); 
  getchar(); 
  return 0; 
} 

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در جاوا

//Fibonacci Series using Recursion 
class fibonacci 
{ 
    static int fib(int n) 
    { 
    if (n <= 1) 
       return n; 
    return fib(n-1) + fib(n-2); 
    } 
       
    public static void main (String args[]) 
    { 
    int n = 9; 
    System.out.println(fib(n)); 
    } 
} 
/* This code is contributed by Rajat Mishra */

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در پایتون

# Function for nth Fibonacci number 
  
def Fibonacci(n): 
    if n<0: 
        print("Incorrect input") 
    # First Fibonacci number is 0 
    elif n==0: 
        return 0
    # Second Fibonacci number is 1 
    elif n==1: 
        return 1
    else: 
        return Fibonacci(n-1)+Fibonacci(n-2) 
  
# Driver Program 
  
print(Fibonacci(9)) 
  
#This code is contributed by Saket Modi

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در #C

// C# program for Fibonacci Series  
// using Recursion 
using System;  
  
public class GFG  
{  
    public static int Fib(int n)  
    {  
        if (n <= 1)  
        {  
            return n;  
        }  
        else
        {  
            return Fib(n - 1) + Fib(n - 2);  
        }  
    }  
          
    // driver code 
    public static void Main(string[] args)  
    {  
        int n = 9; 
        Console.Write(Fib(n));  
    }  
}  
  
// This code is contributed by Sam007

برنامه بازگشتی محاسبه nامین عدد فیبوناچی در PHP

<?php 
// Fibonacci Series  
// using Recursion 
  
// function returns  
// the Fibonacci number 
function fib($n) 
{ 
    if ($n <= 1) 
        return $n; 
    return fib($n - 1) +  
           fib($n - 2); 
} 
  
// Driver Code 
$n = 9; 
echo fib($n); 
  
// This code is contributed by aj_36 
?> 

خروجی

خروجی قطعه کدهای بالا برای n = 9 به صورت زیر است.

34

پیچیدگی زمانی این این روش، (T(n) = T(n-1) + T(n-2 است. می‌توان مشاهده کرد که این پیاده‌سازی کارهای تکرار شونده زیادی را انجام می دهد (درخت بازگشتی که در ادامه آمده، قابل مشاهده است). بنابراین، پیاده‌سازی ارائه شده در بالا، برای محاسبه nامین عدد فیبوناچی، نامناسب است.

fib(5) 
/ \
fib(4) fib(3) 
/ \ / \ 
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)

فضای اضافی (Extra Space) مورد استفاده در روش بالا، اگر فراخوانی تابع برابر با سایز پشته در نظر گرفته شود، برابر با (O(n و در غیر این صورت برابر با (O(۱ است.

روش دوم محاسبه nامین عدد فیبوناچی

در روش دوم محاسبه nامین عدد فیبوناچی، از روش بازگشتی، همراه با برنامه‌نویسی پویا (Dynamic Programming) استفاده شده است. در این روش، می‌توان از کار تکرار شونده‌ای که در راهکار بالا انجام می‌شود اجتناب کرد؛ این کار به وسیله ذخیره‌سازی اعداد فیبوناچی که تاکنون محاسبه شده‌اند انجام می‌شود.

برنامه محاسبه nامین عدد فیبوناچی در C

//Fibonacci Series using Dynamic Programming 
#include<stdio.h> 
  
int fib(int n) 
{ 
  /* Declare an array to store Fibonacci numbers. */
  int f[n+2];   // 1 extra to handle case, n = 0 
  int i; 
  
  /* 0th and 1st number of the series are 0 and 1*/
  f[0] = 0; 
  f[1] = 1; 
  
  for (i = 2; i <= n; i++) 
  { 
      /* Add the previous 2 numbers in the series 
         and store it */
      f[i] = f[i-1] + f[i-2]; 
  } 
  
  return f[n]; 
} 
  
int main () 
{ 
  int n = 9; 
  printf("%d", fib(n)); 
  getchar(); 
  return 0; 
}

برنامه محاسبه nامین عدد فیبوناچی در جاوا

// Fibonacci Series using Dynamic Programming 
class fibonacci 
{ 
   static int fib(int n) 
    { 
    /* Declare an array to store Fibonacci numbers. */
    int f[] = new int[n+2]; // 1 extra to handle case, n = 0 
    int i; 
       
    /* 0th and 1st number of the series are 0 and 1*/
    f[0] = 0; 
    f[1] = 1; 
      
    for (i = 2; i <= n; i++) 
    { 
       /* Add the previous 2 numbers in the series 
         and store it */
        f[i] = f[i-1] + f[i-2]; 
    } 
       
    return f[n]; 
    } 
       
    public static void main (String args[]) 
    { 
        int n = 9; 
        System.out.println(fib(n)); 
    } 
} 
/* This code is contributed by Rajat Mishra */

برنامه محاسبه nامین عدد فیبوناچی در پایتون

# Fibonacci Series using Dynamic Programming  
def fibonacci(n):  
      
    # Taking 1st two fibonacci nubers as 0 and 1  
    FibArray = [0, 1]  
      
    while len(FibArray) < n + 1:  
        FibArray.append(0)  
      
    if n <= 1:  
        return n  
    else:  
        if FibArray[n - 1] == 0:  
            FibArray[n - 1] = fibonacci(n - 1)  
  
        if FibArray[n - 2] == 0:  
            FibArray[n - 2] = fibonacci(n - 2)  
              
    FibArray[n] = FibArray[n - 2] + FibArray[n - 1]  
    return FibArray[n]  
      
print(fibonacci(9))

برنامه محاسبه nامین عدد فیبوناچی در #C

// C# program for Fibonacci Series  
// using Dynamic Programming 
using System; 
class fibonacci { 
      
static int fib(int n) 
    { 
          
        // Declare an array to  
        // store Fibonacci numbers. 
        // 1 extra to handle  
        // case, n = 0 
        int []f = new int[n + 2];  
        int i; 
          
        /* 0th and 1st number of the  
           series are 0 and 1 */
        f[0] = 0; 
        f[1] = 1; 
          
        for (i = 2; i <= n; i++) 
        { 
            /* Add the previous 2 numbers 
               in the series and store it */
            f[i] = f[i - 1] + f[i - 2]; 
        } 
          
        return f[n]; 
    } 
      
    // Driver Code 
    public static void Main () 
    { 
        int n = 9; 
        Console.WriteLine(fib(n)); 
    } 
} 
  
// This code is contributed by anuj_67.

برنامه محاسبه nامین عدد فیبوناچی در PHP

<?php 
//Fibonacci Series using Dynamic 
// Programming 
  
function fib( $n) 
{ 
      
    /* Declare an array to store 
    Fibonacci numbers. */
      
    // 1 extra to handle case, 
    // n = 0 
    $f = array(); 
    $i; 
      
    /* 0th and 1st number of the 
    series are 0 and 1*/
    $f[0] = 0; 
    $f[1] = 1; 
      
    for ($i = 2; $i <= $n; $i++) 
    { 
          
        /* Add the previous 2 
        numbers in the series 
        and store it */
        $f[$i] = $f[$i-1] + $f[$i-2]; 
    } 
      
    return $f[$n]; 
} 
  
$n = 9; 
echo fib($n); 
  
// This code is contributed by 
// anuj_67.  
?> 

روش سوم محاسبه nامین عدد فیبوناچی

این روش، نسبت به روش‌های ارائه شده در بالا، بهینه‌تر است. در اینجا، می‌توان فضای استفاده شده در روش ۲ را با ذخیره‌سازی دو عدد پیشین بهینه کرد. زیرا این دو مورد، تنها اعدادی هستند که برای محاسبه عدد فیبوناچی بعدی در سری مورد نیاز هستند.

برنامه محاسبه nامین عدد فیبوناچی در ++C/C

// Fibonacci Series using Space Optimized Method 
#include<stdio.h> 
int fib(int n) 
{ 
  int a = 0, b = 1, c, i; 
  if( n == 0) 
    return a; 
  for (i = 2; i <= n; i++) 
  { 
     c = a + b; 
     a = b; 
     b = c; 
  } 
  return b; 
} 
  
int main () 
{ 
  int n = 9; 
  printf("%d", fib(n)); 
  getchar(); 
  return 0; 
}

برنامه محاسبه nامین عدد فیبوناچی در جاوا

// Java program for Fibonacci Series using Space 
// Optimized Method 
class fibonacci 
{ 
    static int fib(int n) 
    { 
        int a = 0, b = 1, c; 
        if (n == 0) 
            return a; 
        for (int i = 2; i <= n; i++) 
        { 
            c = a + b; 
            a = b; 
            b = c; 
        } 
        return b; 
    } 
  
    public static void main (String args[]) 
    { 
        int n = 9; 
        System.out.println(fib(n)); 
    } 
} 
  
// This code is contributed by Mihir Joshi

برنامه محاسبه nامین عدد فیبوناچی در پایتون

# Function for nth fibonacci number - Space Optimisataion 
# Taking 1st two fibonacci numbers as 0 and 1 
  
def fibonacci(n): 
    a = 0
    b = 1
    if n < 0: 
        print("Incorrect input") 
    elif n == 0: 
        return a 
    elif n == 1: 
        return b 
    else: 
        for i in range(2,n+1): 
            c = a + b 
            a = b 
            b = c 
        return b 
  
# Driver Program 
  
print(fibonacci(9)) 
  
#This code is contributed by Saket Modi

برنامه محاسبه nامین عدد فیبوناچی در #C

// C# program for Fibonacci Series  
// using Space Optimized Method 
using System; 
  
namespace Fib  
{  
    public class GFG  
    {  
        static int Fib(int n)  
        {  
            int a = 0, b = 1, c = 0;  
              
            // To return the first Fibonacci number  
            if (n == 0) return a;  
      
            for (int i = 2; i <= n; i++)  
            {  
                c = a + b;  
                a = b;  
                b = c;  
            }  
      
            return b;  
        }  
          
    // Driver function 
    public static void Main(string[] args)  
        {  
              
            int n = 9; 
            Console.Write("{0} ", Fib(n));  
        }  
    }  
}  
  
// This code is contributed by Sam007.

برنامه محاسبه nامین عدد فیبوناچی در PHP

<?php 
// PHP program for Fibonacci Series  
// using Space Optimized Method 
  
function fib( $n) 
{ 
    $a = 0;  
    $b = 1;  
    $c; 
    $i; 
    if( $n == 0) 
        return $a; 
    for($i = 2; $i <= $n; $i++) 
    { 
        $c = $a + $b; 
        $a = $b; 
        $b = $c; 
    } 
    return $b; 
} 
  
// Driver Code 
$n = 9; 
echo fib($n); 
  
// This code is contributed by anuj_67. 
?>

خروجی

خروجی قطعه کدهای بالا برای n = 9 به صورت زیر است.

34

پیچیدگی زمانی این الگوریتم از درجه (O(n و فضای اضافی آن از (O(1 است.

روش چهارم محاسبه nامین عدد فیبوناچی

در اینجا، از به توان رساندن ماتریس {{1,1},{1,0}} برای محاسبه nامین عدد فیبوناچی استفاده شده است. پیچیدگی زمانی این راهکار از درجه (O(n است؛ دلیل این امر آن است که اگر n بار ماتریس {{M = {{1,1},{1,0 در خودش ضرب شود، (به بیان دیگر، توان (M, n) محاسبه شود) n+1اُمین عدد فیبوناچی به عنوان عنصری در سطر و ستون (0, 0) در ماتریس نتیجه به دست می‌آید. ارائه ماتریس، عبارت بسته زیر را برای اعداد فیبوناچی به دست می‌دهد.

$$\begin{bmatrix}1 & 1 \\1 & 0 \end{bmatrix} ^ n = \begin{bmatrix}F_{n+1} & F_{n} \\F_{n} & F_{n-1} \end{bmatrix}$$

برنامه محاسبه nامین عدد فیبوناچی در C

#include <stdio.h> 
  
/* Helper function that multiplies 2 matrices F and M of size 2*2, and 
  puts the multiplication result back to F[][] */
void multiply(int F[2][2], int M[2][2]); 
  
/* Helper function that calculates F[][] raise to the power n and puts the 
  result in F[][] 
  Note that this function is designed only for fib() and won't work as general 
  power function */
void power(int F[2][2], int n); 
  
int fib(int n) 
{ 
  int F[2][2] = {{1,1},{1,0}}; 
  if (n == 0) 
      return 0; 
  power(F, n-1); 
  
  return F[0][0]; 
} 
  
void multiply(int F[2][2], int M[2][2]) 
{ 
  int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0]; 
  int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1]; 
  int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0]; 
  int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1]; 
  
  F[0][0] = x; 
  F[0][1] = y; 
  F[1][0] = z; 
  F[1][1] = w; 
} 
  
void power(int F[2][2], int n) 
{ 
  int i; 
  int M[2][2] = {{1,1},{1,0}}; 
  
  // n - 1 times multiply the matrix to {{1,0},{0,1}} 
  for (i = 2; i <= n; i++) 
      multiply(F, M); 
} 
  
/* Driver program to test above function */
int main() 
{ 
  int n = 9; 
  printf("%d", fib(n)); 
  getchar(); 
  return 0; 
}

برنامه محاسبه nامین عدد فیبوناچی در جاوا

class fibonacci 
{ 
      
    static int fib(int n) 
    { 
    int F[][] = new int[][]{{1,1},{1,0}}; 
    if (n == 0) 
        return 0; 
    power(F, n-1); 
      
       return F[0][0]; 
    } 
       
     /* Helper function that multiplies 2 matrices F and M of size 2*2, and 
     puts the multiplication result back to F[][] */
    static void multiply(int F[][], int M[][]) 
    { 
    int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0]; 
    int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1]; 
    int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0]; 
    int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1]; 
       
    F[0][0] = x; 
    F[0][1] = y; 
    F[1][0] = z; 
    F[1][1] = w; 
    } 
  
    /* Helper function that calculates F[][] raise to the power n and puts the 
    result in F[][] 
    Note that this function is designed only for fib() and won't work as general 
    power function */
    static void power(int F[][], int n) 
    { 
    int i; 
    int M[][] = new int[][]{{1,1},{1,0}}; 
      
    // n - 1 times multiply the matrix to {{1,0},{0,1}} 
    for (i = 2; i <= n; i++) 
        multiply(F, M); 
    } 
       
    /* Driver program to test above function */
    public static void main (String args[]) 
    { 
    int n = 9; 
    System.out.println(fib(n)); 
    } 
} 
/* This code is contributed by Rajat Mishra */

برنامه محاسبه nامین عدد فیبوناچی در پایتون ۳

# Helper function that multiplies  
# 2 matrices F and M of size 2*2,  
# and puts the multiplication 
# result back to F[][]  
  
# Helper function that calculates  
# F[][] raise to the power n and  
# puts the result in F[][] 
# Note that this function is  
# designed only for fib() and  
# won't work as general 
# power function  
def fib(n): 
    F = [[1, 1], 
         [1, 0]] 
    if (n == 0): 
        return 0
    power(F, n - 1) 
      
    return F[0][0] 
  
def multiply(F, M): 
  
    x = (F[0][0] * M[0][0] + 
         F[0][1] * M[1][0]) 
    y = (F[0][0] * M[0][1] +
         F[0][1] * M[1][1]) 
    z = (F[1][0] * M[0][0] + 
         F[1][1] * M[1][0]) 
    w = (F[1][0] * M[0][1] + 
         F[1][1] * M[1][1]) 
      
    F[0][0] = x 
    F[0][1] = y 
    F[1][0] = z 
    F[1][1] = w 
  
def power(F, n): 
  
    M = [[1, 1], 
         [1, 0]] 
  
    # n - 1 times multiply the 
    # matrix to {{1,0},{0,1}} 
    for i in range(2, n + 1): 
        multiply(F, M) 
  
# Driver Code 
if __name__ == "__main__": 
    n = 9
    print(fib(n)) 
  
# This code is contributed  
# by ChitraNayal

برنامه محاسبه nامین عدد فیبوناچی در #C

// C# program to find fibonacci number. 
using System; 
  
class GFG { 
      
    static int fib(int n) 
    { 
        int [,]F = new int[,] {{1, 1}, 
                               {1, 0} }; 
        if (n == 0) 
            return 0; 
        power(F, n-1); 
          
        return F[0,0]; 
    } 
      
    /* Helper function that multiplies 2  
    matrices F and M of size 2*2, and puts 
    the multiplication result back to F[][] */
    static void multiply(int [,]F, int [,]M) 
    { 
        int x = F[0,0]*M[0,0] + F[0,1]*M[1,0]; 
        int y = F[0,0]*M[0,1] + F[0,1]*M[1,1]; 
        int z = F[1,0]*M[0,0] + F[1,1]*M[1,0]; 
        int w = F[1,0]*M[0,1] + F[1,1]*M[1,1]; 
          
        F[0,0] = x; 
        F[0,1] = y; 
        F[1,0] = z; 
        F[1,1] = w; 
    } 
  
    /* Helper function that calculates F[][]  
    raise to the power n and puts the result 
    in F[][] Note that this function is designed 
    only for fib() and won't work as general 
    power function */
    static void power(int [,]F, int n) 
    { 
        int i; 
        int [,]M = new int[,]{{1, 1}, 
                              {1, 0} }; 
          
        // n - 1 times multiply the matrix to 
        // {{1,0},{0,1}} 
        for (i = 2; i <= n; i++) 
            multiply(F, M); 
    } 
      
    /* Driver program to test above function */
    public static void Main () 
    { 
        int n = 9; 
        Console.WriteLine(fib(n)); 
    } 
} 
  
// This code is contributed by anuj_67.

برنامه محاسبه nامین عدد فیبوناچی در PHP

<?php  
// PHP program for above approach 
function fib($n) 
{ 
    $F = array(array(1, 1), 
               array(1, 0)); 
    if ($n == 0) 
        return 0; 
    power($F, $n - 1); 
      
    return $F[0][0]; 
} 
  
function multiply(&$F, &$M) 
{ 
$x = $F[0][0] * $M[0][0] +  
     $F[0][1] * $M[1][0]; 
$y = $F[0][0] * $M[0][1] +  
     $F[0][1] * $M[1][1]; 
$z = $F[1][0] * $M[0][0] +  
     $F[1][1] * $M[1][0]; 
$w = $F[1][0] * $M[0][1] + 
     $F[1][1] * $M[1][1]; 
  
$F[0][0] = $x; 
$F[0][1] = $y; 
$F[1][0] = $z; 
$F[1][1] = $w; 
} 
  
function power(&$F, $n) 
{ 
    $M = array(array(1, 1), 
               array(1, 0)); 
      
    // n - 1 times multiply the 
    // matrix to {{1,0},{0,1}} 
    for ($i = 2; $i <= $n; $i++) 
        multiply($F, $M); 
} 
  
// Driver Code 
$n = 9; 
echo fib($n); 
  
// This code is contributed  
// by ChitraNayal 
?>

پیچیدگی زمانی این روش، از درجه (O(n و فضای اضافی آن از درجه (O(1 است.

روش پنجم محاسبه nامین عدد فیبوناچی

این روش، بهینه شده روش پیشین است. در واقع، روش چهارم را می‌توان به نوعی بهینه کرد که با پیچیدگی زمانی (O(Logn کار کند. می‌توان از ضرب بازگشتی برای محاسبه (power(M, n در روش پیشین، استفاده کرد.

برنامه محاسبه nامین عدد فیبوناچی در C

#include <stdio.h> 
  
void multiply(int F[2][2], int M[2][2]); 
  
void power(int F[2][2], int n); 
  
/* function that returns nth Fibonacci number */
int fib(int n) 
{ 
  int F[2][2] = {{1,1},{1,0}}; 
  if (n == 0) 
    return 0; 
  power(F, n-1); 
  return F[0][0]; 
} 
  
/* Optimized version of power() in method 4 */
void power(int F[2][2], int n) 
{ 
  if( n == 0 || n == 1) 
      return; 
  int M[2][2] = {{1,1},{1,0}}; 
  
  power(F, n/2); 
  multiply(F, F); 
  
  if (n%2 != 0) 
     multiply(F, M); 
} 
  
void multiply(int F[2][2], int M[2][2]) 
{ 
  int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0]; 
  int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1]; 
  int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0]; 
  int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1]; 
  
  F[0][0] = x; 
  F[0][1] = y; 
  F[1][0] = z; 
  F[1][1] = w; 
} 
  
/* Driver program to test above function */
int main() 
{ 
  int n = 9; 
  printf("%d", fib(9)); 
  getchar(); 
  return 0; 
}

برنامه محاسبه nامین عدد فیبوناچی در جاوا

//Fibonacci Series using  Optimized Method 
class fibonacci 
{ 
    /* function that returns nth Fibonacci number */
    static int fib(int n) 
    { 
    int F[][] = new int[][]{{1,1},{1,0}}; 
    if (n == 0) 
        return 0; 
    power(F, n-1); 
       
    return F[0][0]; 
    } 
       
    static void multiply(int F[][], int M[][]) 
    { 
    int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0]; 
    int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1]; 
    int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0]; 
    int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1]; 
      
    F[0][0] = x; 
    F[0][1] = y; 
    F[1][0] = z; 
    F[1][1] = w; 
    } 
       
    /* Optimized version of power() in method 4 */
    static void power(int F[][], int n) 
    { 
    if( n == 0 || n == 1) 
      return; 
    int M[][] = new int[][]{{1,1},{1,0}}; 
       
    power(F, n/2); 
    multiply(F, F); 
       
    if (n%2 != 0) 
       multiply(F, M); 
    } 
      
    /* Driver program to test above function */ 
    public static void main (String args[]) 
    { 
         int n = 9; 
     System.out.println(fib(n)); 
    } 
} 
/* This code is contributed by Rajat Mishra */

برنامه محاسبه nامین عدد فیبوناچی در پایتون ۳

# Fibonacci Series using  
# Optimized Method 
  
# function that returns nth  
# Fibonacci number  
def fib(n): 
      
    F = [[1, 1], 
         [1, 0]] 
    if (n == 0): 
        return 0
    power(F, n - 1) 
          
    return F[0][0] 
      
def multiply(F, M): 
      
    x = (F[0][0] * M[0][0] + 
         F[0][1] * M[1][0]) 
    y = (F[0][0] * M[0][1] + 
         F[0][1] * M[1][1]) 
    z = (F[1][0] * M[0][0] + 
         F[1][1] * M[1][0]) 
    w = (F[1][0] * M[0][1] + 
         F[1][1] * M[1][1]) 
      
    F[0][0] = x 
    F[0][1] = y 
    F[1][0] = z 
    F[1][1] = w 
          
# Optimized version of 
# power() in method 4  
def power(F, n): 
  
    if( n == 0 or n == 1): 
        return; 
    M = [[1, 1], 
         [1, 0]]; 
          
    power(F, n // 2) 
    multiply(F, F) 
          
    if (n % 2 != 0): 
        multiply(F, M) 
      
# Driver Code 
if __name__ == "__main__": 
    n = 9
    print(fib(n)) 
  
# This code is contributed  
# by ChitraNayal

برنامه محاسبه nامین عدد فیبوناچی در #C

// Fibonacci Series using  
// Optimized Method 
using System; 
  
class GFG 
{ 
/* function that returns  
nth Fibonacci number */
static int fib(int n) 
{ 
int[,] F = new int[,]{{1, 1},  
                      {1, 0}}; 
if (n == 0) 
    return 0; 
power(F, n - 1); 
  
return F[0, 0]; 
} 
  
static void multiply(int[,] F,  
                     int[,] M) 
{ 
int x = F[0, 0] * M[0, 0] +  
        F[0, 1] * M[1, 0]; 
int y = F[0, 0] * M[0, 1] +  
        F[0, 1] * M[1, 1]; 
int z = F[1, 0] * M[0, 0] +  
        F[1, 1] * M[1, 0]; 
int w = F[1, 0] * M[0, 1] +  
        F[1, 1] * M[1, 1]; 
  
F[0, 0] = x; 
F[0, 1] = y; 
F[1, 0] = z; 
F[1, 1] = w; 
} 
  
/* Optimized version of  
power() in method 4 */
static void power(int[,] F, int n) 
{ 
if( n == 0 || n == 1) 
return; 
int[,] M = new int[,]{{1, 1},  
                      {1, 0}}; 
  
power(F, n / 2); 
multiply(F, F); 
  
if (n % 2 != 0) 
multiply(F, M); 
} 
  
// Driver Code 
public static void Main () 
{ 
    int n = 9; 
    Console.Write(fib(n)); 
} 
} 
  
// This code is contributed 
// by ChitraNayal

پیچیدگی زمانی این روش، از درجه (O(Logn است. اگر اندازه پشته فراخوانی تابع در نظر گرفته شود، فضای اضافی این روش از درجه (O(Logn و در غیر این صورت، از (O(1 است.

روش ششم محاسبه nامین عدد فیبوناچی

در زیر، یک فرمول بازگشتی جالب توجه برای پیدا کردن nامین عدد فیبوناچی در زمان (O(Log n ارائه شده است.

اگر n زوج است، k = n/2:

F(n) = [2*F(k-1) + F(k)]*F(k)

اگر n فرد است، k = (n + 1)/2:

F(n) = F(k)*F(k) + F(k-1)*F(k-1)

این رابطه را می‌توان از معادله ماتریس بالا به دست آورد.

$$\begin{bmatrix}1 & 1 \\1 & 0 \end{bmatrix} ^ n = \begin{bmatrix}F_{n+1} & F_{n} \\F_{n} & F_{n-1} \end{bmatrix}$$

با دترمینان گرفتن از دو طرف معادله، داریم:

$$(-1)^n = F_{n+1}F_{n-1} – F_{n}^2$$

همچنین، با توجه به اینکه رابطه $$ A^nA^m = A^n+m$$ برای هر ماتریس مربعی A برقرار است، ماتریس‌های همانی زیر را می‌توان به دست آورد (این موارد، از دو ضریب مختلف ضرب داخلی ماتریس‌ها به دست آمده‌اند).

$$F_{m} F_{n} + F_{m – 1} F_{n – 1} = F_{m + n – 1}$$

با قرار دادن n = n+1 رابطه زیر به دست می آید:

$$F_{m}F_{n+1} + F_{m – 1}F_{n} = F_{m + n}$$

با قرار دادن m = n روابط زیر حاصل می‌شوند:

$$F_{2n-1} = F_{n}^2 + F_{n-1} ^ 2$$

$$F_{2n} = (F_{n – 1} + F_{n+1})F_{n} = (2F_{n-1}+F_{n})F_{n}$$

برای اثبات این رابطه، باید اقدامات زیر را انجام داد:

• اگر n زوج است، می‌توان $$k = \frac{n}{2}$$ را قرار داد.
• اگر n فرد است، می‌توان $$k = \frac{n + 1}{2}$$ را قرار داد.

در ادامه، پیاده‌سازی روش بالا انجام شده است.

برنامه محاسبه nامین عدد فیبوناچی در ++C

// C++ Program to find n'th fibonacci Number in 
// with O(Log n) arithmatic operations 
#include <bits/stdc++.h> 
using namespace std; 
  
const int MAX = 1000; 
  
// Create an array for memoization 
int f[MAX] = {0}; 
  
// Returns n'th fuibonacci number using table f[] 
int fib(int n) 
{ 
    // Base cases 
    if (n == 0) 
        return 0; 
    if (n == 1 || n == 2) 
        return (f[n] = 1); 
  
    // If fib(n) is already computed 
    if (f[n]) 
        return f[n]; 
  
    int k = (n & 1)? (n+1)/2 : n/2; 
  
    // Applyting above formula [Note value n&1 is 1 
    // if n is odd, else 0. 
    f[n] = (n & 1)? (fib(k)*fib(k) + fib(k-1)*fib(k-1)) 
           : (2*fib(k-1) + fib(k))*fib(k); 
  
    return f[n]; 
} 
  
/* Driver program to test above function */
int main() 
{ 
    int n = 9; 
    printf("%d ", fib(n)); 
    return 0; 
} 

برنامه محاسبه nامین عدد فیبوناچی در جاوا

// Java Program to find n'th fibonacci  
// Number with O(Log n) arithmetic operations 
import java.util.*; 
  
class GFG { 
      
    static int MAX = 1000; 
    static int f[]; 
      
    // Returns n'th fibonacci number using  
    // table f[] 
    public static int fib(int n) 
    { 
        // Base cases 
        if (n == 0) 
            return 0; 
              
        if (n == 1 || n == 2) 
            return (f[n] = 1); 
       
        // If fib(n) is already computed 
        if (f[n] != 0) 
            return f[n]; 
       
        int k = (n & 1) == 1? (n + 1) / 2 
                            : n / 2; 
       
        // Applyting above formula [Note value 
        // n&1 is 1 if n is odd, else 0. 
        f[n] = (n & 1) == 1? (fib(k) * fib(k) +  
                        fib(k - 1) * fib(k - 1)) 
                       : (2 * fib(k - 1) + fib(k))  
                       * fib(k); 
       
        return f[n]; 
    } 
      
    /* Driver program to test above function */
    public static void main(String[] args)  
    { 
        int n = 9; 
        f= new int[MAX]; 
        System.out.println(fib(n)); 
    } 
} 
      
// This code is contributed by Arnav Kr. Mandal.

برنامه محاسبه nامین عدد فیبوناچی در پایتون

# Python 3 Program to find n'th fibonacci Number in 
# with O(Log n) arithmatic operations 
MAX = 1000
  
# Create an array for memoization 
f = [0] * MAX
  
# Returns n'th fuibonacci number using table f[] 
def fib(n) : 
    # Base cases 
    if (n == 0) : 
        return 0
    if (n == 1 or n == 2) : 
        f[n] = 1
        return (f[n]) 
  
    # If fib(n) is already computed 
    if (f[n]) : 
        return f[n] 
  
    if( n & 1) : 
        k = (n + 1) // 2
    else :  
        k = n // 2
  
    # Applyting above formula [Note value n&1 is 1 
    # if n is odd, else 0. 
    if((n & 1) ) : 
        f[n] = (fib(k) * fib(k) + fib(k-1) * fib(k-1)) 
    else : 
        f[n] = (2*fib(k-1) + fib(k))*fib(k) 
  
    return f[n] 
  
  
# Driver code 
n = 9
print(fib(n)) 
  
  
# This code is contributed by Nikita Tiwari.

برنامه محاسبه nامین عدد فیبوناچی در #C

// C# Program to find n'th  
// fibonacci Number with  
// O(Log n) arithmetic operations 
using System; 
  
class GFG 
{ 
  
static int MAX = 1000; 
static int[] f; 
  
// Returns n'th fibonacci  
// number using table f[] 
public static int fib(int n) 
{ 
    // Base cases 
    if (n == 0) 
        return 0; 
          
    if (n == 1 || n == 2) 
        return (f[n] = 1); 
  
    // If fib(n) is already  
    // computed 
    if (f[n] != 0) 
        return f[n]; 
  
    int k = (n & 1) == 1 ? (n + 1) / 2 
                         : n / 2; 
  
    // Applyting above formula  
    // [Note value n&1 is 1 if  
    // n is odd, else 0. 
    f[n] = (n & 1) == 1 ? (fib(k) * fib(k) +  
                           fib(k - 1) * fib(k - 1)) 
                        : (2 * fib(k - 1) + fib(k)) *  
                                            fib(k); 
  
    return f[n]; 
} 
  
// Driver Code 
static void Main()  
{ 
    int n = 9; 
    f = new int[MAX]; 
    Console.WriteLine(fib(n)); 
} 
} 
  
// This code is contributed by mits

برنامه محاسبه nامین عدد فیبوناچی در PHP

خروجی

خروجی قطعه کدهای بالا برای n = 9 به صورت زیر است.

34

پیچیدگی زمانی این روش، از درجه (O(Log n است، زیرا در هر فراخوانی بازگشتی، مساله به نیمی تقسیم (شکسته) می‌شود.

روش هفتم محاسبه nامین عدد فیبوناچی

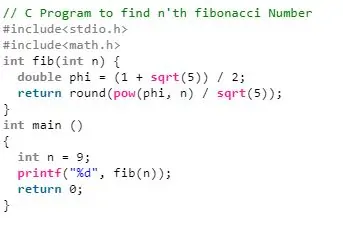
در این روش، فرمول به طور مستقیم برای nامین عبارت سری فیبوناچی پیاده‌سازی می‌شود.

$$F_{n} = \frac{\{[\frac{\sqrt{5}+1}{2}]^{n}\}}{\sqrt{5}}$$

برنامه محاسبه nامین عدد فیبوناچی در ++C

// C++ Program to find n'th fibonacci Number 
#include<iostream> 
#include<cmath> 
  
int fib(int n) { 
  double phi = (1 + sqrt(5)) / 2; 
  return round(pow(phi, n) / sqrt(5)); 
} 
  
// Driver Code 
int main () 
{ 
  int n = 9; 
  std::cout << fib(n) << std::endl; 
  return 0; 
} 
//This code is contributed by Lokesh Mohanty.

برنامه محاسبه nامین عدد فیبوناچی در C

برنامه محاسبه nامین عدد فیبوناچی در جاوا

برنامه محاسبه nامین عدد فیبوناچی در #C

برنامه محاسبه nامین عدد فیبوناچی در PHP

خروجی

خروجی قطعه کد بالا، برای n = 9 به صورت زیر است.

34

پیچیدگی زمانی این روش از درجه (O(1 و پیچیدگی فضایی آن نیز از درجه (O(1 است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• برنامه تشخیص اعداد اول در پایتون — به زبان ساده
• برنامه تجزیه عدد به عوامل اول آن — به زبان ساده

^^