اندازه پذیر لبگ و مجموعه بورل — به زبان ساده

در این نوشتار سعی داریم یک مجموعه اندازهپذیر لبگ را به شکلی ایجاد کنیم که یک مجموعه بورل نباشد. اغلب تصور میشود که مجموعههای اندازهپذیر لبگ از اعداد حقیقی یک مجموعه بورل نیز هستند. به این ترتیب با ایجاد مثالی که این موضوع را نقض میکند، متن این مطلب را شکل میدهیم. البته در اکثر مواقع مجموعه بورل و اندازه پذیری لبگ با هم یکسان دیده میشوند. پس به دنبال پیدا کردن مجموعهای هستیم که اندازه پذیر لبگ بوده ولی مجموعه بورل نیست.
به منظور آشنایی بیشتر با نظریه اندازه و مجموعههای بورل و لبگ بهتر است نوشتارهای دیگر مجله فرادرس با عنوانهای اندازه لبگ در نظریه اندازه | به زبان ساده و مجموعه بورل در نظریه اندازه | به زبان ساده را مطالعه کنید. همچنین خواندن مطالب نظریه اندازه در ریاضیات — مفاهیم و کاربردها و فضای توپولوژیک در ریاضیات — به زبان ساده نیز خالی از لطف نیست.
اندازه پذیر لبگ و مجموعه بورل
همانطور که میدانید مجموعه بورل از «مجموعههای باز» (Open Sets) تشکیل شده است. در طرف مقابل مجموعههای اندازه پذیر لبگ براساس مجموعههای باز و مجموعههای صفر (Null Sets) تشکیل میشوند. به این ترتیب اگر گردایهای از مجموعههای بورل و نیز گردایه مجموعههای اندازهپذیر لبگ باشند، رابطه زیر بین آنها مسجل است.
مقدمات درباره مجموعه اندازهپذیر لبگ و مجموعه بورل
به منظور پیدا کردن مجموعهای که در بوده ولی به تعلق ندارد از دو واقعیت و اصل استفاده میکنیم.
- هر مجموعهای از با اندازه مثبت شامل یک زیر مجموعه اندازهناپذیر لبگ (Lebesgue Non-measurable) است.
- بیشتر مثالهای نقض در مورد مجموعه اندازه پذیر لبگ و مجموعه بورل مربوط به مجموعه کانتور است.
البته گزاره آخر، واقعا به عنوان یک اصل مطرح نیست ولی امروزه بحث در مورد مجموعه کانتور بسیار داغ و به روز است.
در این نوشتار سعی داریم به کمک یک «نگاشت همریخت» (Homeomorphism) که در حقیقت تابع پیوسته و معکوسپذیر از بازه به است، هر مجموعه یا زیرمجموعه کانتور با اندازه صفر را به یک مجموعه با اندازه یک تبدیل کنیم.
با توجه به واقعیت شماره ۱، میدانیم که مجموعهای با اندازه ۱، شامل یک زیرمجموعه اندازهناپذیر است. اگر چنین مجموعهای را بنامیم، پیش تصویر یک مجموعه اندازهپذیر لبگ بوده که بورل اندازهپذیر نیست.
در ادامه به بررسی این موضوع پرداخته و به این نکته نیز توجه داریم که مبنای کار ما همریختی است و به کمک مجموعه کانتور نشان میدهیم که همریختی همیشه حافظ خاصیت اندازهپذیری (Measurable) نیست.
ادعا در مورد اندازه لبگ و مجموعه بورل
ابتدا از تعریف تابع از به آغاز میکنیم. اگر تابع از به یک «تابع کانتور» (Cantor Function) باشد، آنگاه تابع را به صورت زیر در نظر میگیریم.
نمودار تابع در تصویر ۱ دیده میشود. همانطور که مشخص است شیب خط در زمانی که منحنی پیوسته است، برابر با ۱ و در نقاط ناپیوستگی، مشتق موجود نیست.
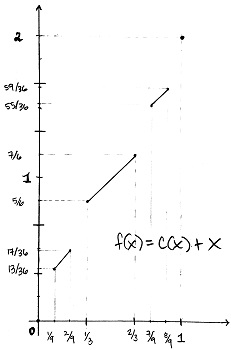
- مشخص است که تابع اکیدا صعودی است. زیرا مشتق تابع «تقریبا همه جا» (Almost everywhere) برابر با ۱ بوده و مثبت است. زیرا مشتق تابع کانتور تقریبا همه جا صفر است.
- تابع پیوسته است زیرا هر دو بخش آن یعنی و پیوسته بوده و جمع دو تابع پیوسته، نیز پیوسته است.
- معکوس تابع موجود است. زیرا تابع یک تابع «یک به یک و پوشا» (One to One Corresponding) است. به این علت تابع یک به یک است که یک تابع صعودی است. از طرفی تابع به دلیل «قضیه مقدار میانی» (Intermediate Value Theorem) پوشا نیز هست. واضح است که و تابع پیوسته بوده و شرایط قضیه مقدار میانی در بازه برقرار است.
- معکوس تابع یعنی نیز پیوسته است در نتیجه تابع ، «همریخت» (Homeomorphism) است. اثبات این قضیه در ضمیمه آماده است.
این موضوعات بیانگر آن است که تابع یک نگاشت از است که با حذف مجموعه کانتور روی اندازه لبگ عمل میکند ولی طول برابری برحسب اندازه لبگ از مجموعه اول دارد. اثبات این قضیه نیز در ضمیمه آورده شده است. به این ترتیب داریم:
ولی چون به صورت نوشته میشود خواهیم داشت:
در نتیجه میتوان نوشت:
براساس رابطه بالا نتیجه میگیریم که بوده و شامل یک زیر مجموعه اندازهناپذیر مثل است.
به این ترتیب ادعا میکنیم که لبگ-اندازهپذیر بوده ولی یک مجموعه بورل نیست. برای اثبات این موضوع به مقدمات و لمی (Lema) احتیاج داریم که در ادامه به معرفی و اثبات آن میپردازیم.
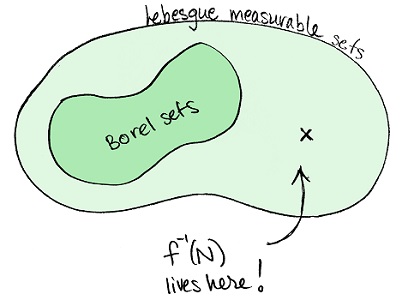
صورت لم:
یک تابع اکیدا صعودی که روی یک بازه تعریف شده، نگاشتی از یک مجموعه بورل به مجموعه بورل دیگر ایجاد میکند.
اثبات لم:
اثبات این لم را در تمرینات ۴۵ تا ۴۷ فصل دوم کتاب «آنالیز حقیقی» (Real Analyses) «رویدن» (Royden) آمده است. ما هم همان روال را طی خواهیم کرد.
فرض کنید اکیدا صعودی روی بازهای از اعداد حقیقی باشد، با استفاده از گزارههای قبلی میدانیم که چنین تابعی، همریخت است. این امر به ما نشان میدهد که یک نگاشت از مجموعه بورل به مجموعه بورل است. برای نشان دادن این موضوع کافی است که برای هر تابع پیوستهای مثل مجموعه زیر، یک «سیگما-جبر» (-Algebra) شامل مجموعههای باز باشد.
اگر بتوانیم این موضوع را مشخص کنیم، نتیجه خواهیم گرفت که مجموعه شامل همه مجموعههای بورل است و در نتیجه تابع را همان در نظر خواهیم گرفت که میدانیم پیوسته است. به این ترتیب برای هر مجموعه بورلی مثل داریم:
که طرف راست تساوی یک مجموعه بورل است. برای نشان دادن این موضوع به ترتیب زیر عمل میکنیم:
- اگر باشد آنگاه زیرا یک سیگما-جبر است در نتیجه خواهد بود.
- اگر باشد، آنگاه ، زیرا یک سیگما-میدان بوده در نتیجه .
- اگر یک مجموعه باز باشد، نیز یک مجموعه باز بوده و عناصر آن مجموعههای بورل هستند. در نتیجه در سیگما میدان قرار خواهد داشت.
همانطور که میبینید دو قسمت اول، سیگما میدان بودن را نشان داده و قسمت سوم نیز بیانگر آن است که معکوس تابع نیز یک مجموعه باز و بورل خواهد بود.
حال با توجه به این لم، آماده هستیم که ادعای خود را اثبات کنیم.
اثبات وجود مجموعه اندازه پذیر لبگ که مجموعه بورل نیست
از آنجایی که است میدانیم که و اندازهپذیر بوده و اندازه آن صفر است. علت آن است که این مجموعه زیر مجموعه یک مجموعه با اندازه صفر بوده و اندازه لبگ نیز یک اندازه کامل است.
از طرفی یک مجموعه بورل نیست. زیرا اگر چنین بود، چون یک نگاشت از مجموعه بورل به بورل محسوب میشود، طبق لم گفته شده، باید داشته باشیم:
که ، یک مجموعه بورل است. ولی از آنجایی که یک مجموعه اندازهپذیر نیست، چنین امری امکانپذیر نخواهد بود. این موضوع ادعای ما را ثابت میکند.
ضمیمه
همانطور که گفته شد، برای اثبات بعضی از گزارهها احتیاج به محاسبات دیگری است که در این قسمت به آنها خواهیم پرداخت.
اثبات پیوستگی و باز بودن
فرض کنید که و از طرفی یک مجموعه باز (Open Set) باشد. در نتیجه یک مجموعه فشرده بوده، پس، بسته و کراندار خواهد بود. این گزارهها را به صورت زیر بیان میکنیم:
اثبات یکسان بودن اندازه تابع با اندازه بازه
این موضوع به سادگی با ثابت بودن مقدار تابع کانتور روی هر بازهای که زیر مجموعه باشد، مشخص میشود.
فرض کنید در مورد بازه داشته باشیم:
در نتیجه رابطههای زیر برقرار خواهند بود.
خلاصه و جمعبندی
همانطور که در این نوشتار خواندید، با توجه به ریاضیات مدرن و با تکیه به نظریه اندازه (Measure Theory)، هدف متن، ایجاد ساختاری بود که توسط یک مثال نشان دهیم، مجموعهای اندازه پذیر لبگ وجود دارد که مجموعه بورل نیست. در این میان به کمک مجموعه کانتور و قضیههایی، ساختار چنین مجموعهای را ارائه کرده و به کمک مثالی آن را معرفی کردیم. این کار از این جهت مهم است که به کمک آن نشان میدهیم، هر مجموعه اندازه پذیر لبگ و مجموعه بورل یکسان نیستند.













اثبات به روش تکرار زیر بازه و برهان خلف که بازه یکه [۰,۱] فشرده هست