مجموعه بورل در نظریه اندازه | به زبان ساده

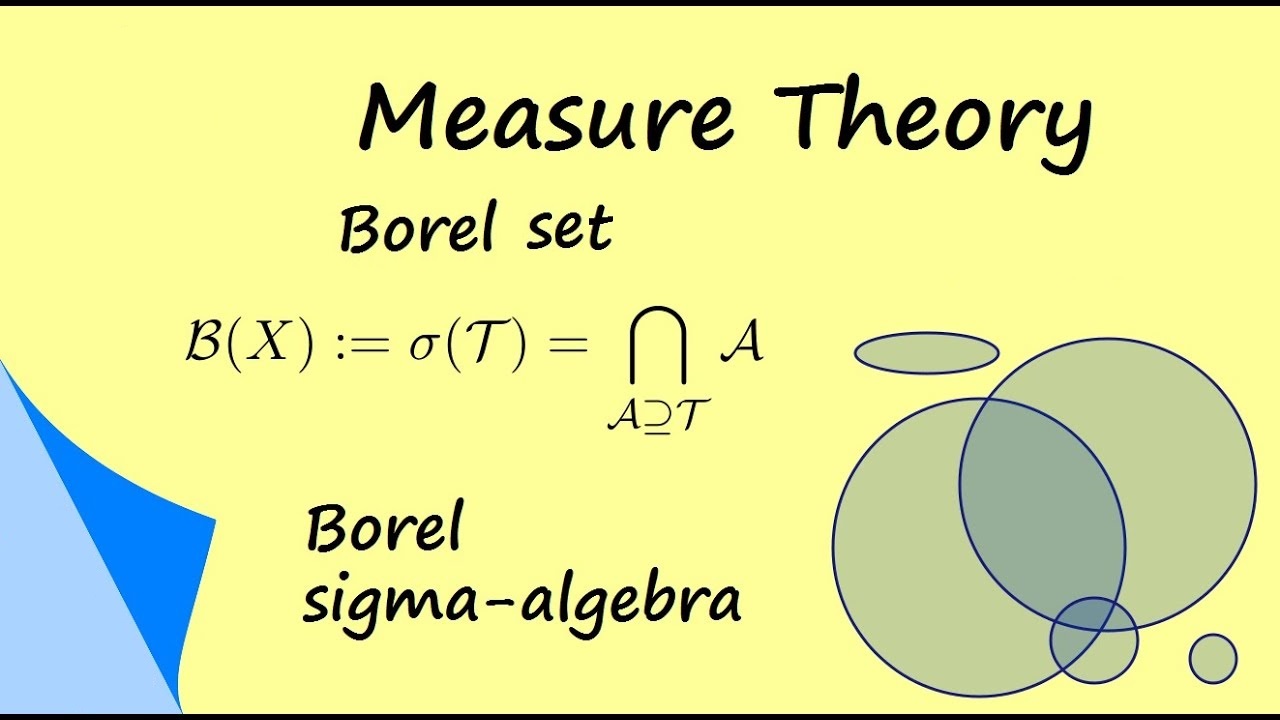
در ریاضیات و فضای توپولوژیک (Topological Space)، یک مجموعه بورل (Borel set) بوسیله «مجموعه‌های باز» (Open sets) یا به صورت معادل با «مجموعه‌های بسته» (Closed sets) قابل بیان و توصیف است. اهمیت چنین مجموعه‌هایی در آنالیز ریاضی (Mathematical Analysis) و نظریه اندازه (Measure Theory) بسیار زیاد است. از طرفی در نظریه احتمال (Probability Theory) و تعریف متغیر تصادفی (Random Variable) از مجموعه بورل و تعریف آن‌ها، بسیار صحبت می‌شود. به همین دلیل این نوشتار از مجله فرادرس را به مجموعه بورل در نظریه اندازه اختصاص داده‌ایم تا علاوه بر آشنایی با مفاهیم آن، از کاربردهای چنین مجموعه‌هایی در آمار و احتمال آگاه شوید.

برای آشنایی بیشتر با فضای توپولوژیک و نظریه اندازه پیشنهاد می‌شود به عنوان مقدمه، نوشتارهای دیگر مجله فرادرس با عنوان‌های نظریه اندازه در ریاضیات — مفاهیم و کاربردها و میدان، حلقه و گروه در ریاضی — مفاهیم اولیه را مطالعه کنید. همچنین خواندن نوشتارهای متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و اندازه لبگ در نظریه اندازه | به زبان ساده نیز خالی از لطف نیست.

مجموعه بورل در نظریه اندازه

مجموعه‌های بورل، در نظریه اندازه بسیار با اهمیت هستند زیرا با مجموعه اعداد حقیقی و همچنین مفاهیم مجموعه‌ها باز و بسته، ارتباط دارند. در واقع هر اندازه روی مجموعه‌های باز (Open set) یا بسته (Closed set) از یک فضای برگرفته از مجموعه اعداد حقیقی ساخته می‌شود که مجموعه‌های بورل هستند. هر اندازه‌ای که روی مجموعه‌های بورل تعریف شود، به عنوان یک «اندازه بورل» (Borel Measure) خواهد بود. به این ترتیب مجموعه‌های بورل راه را برای تعریف اندازه بورل باز می‌کنند.

فیلم آموزش مبانی آنالیز ریاضی در فرادرس

کلیک کنید

در یک فضای توپولوژیک (مثل $$X$$)، گردایه تشکیل شده از همه مجموعه‌های بورل از آن فضا، یک «سیگما-جبر»  ($$\sigma \text{-algebra}$$) می‌سازد که به «جبر بورل» (Borel algebra) یا «سیگما-جبر بورل» (Borel $$\sigma$$-algebra) معروف است. جبر بورل ساخته شده در $$X$$، کوچکترین سیگما-جبری است که از همه مجموعه‌های باز (بسته) این توپولوژی ساخته شده است.

نکته: سیگما-جبر یا سیگما میدان ($$\sigma \text{-field}$$)، روی یک مجموعه مثل $$A$$ تعریف شده و گردایه‌ای از زیرمجموعه‌های آن محسوب می‌شود که نسبت به متمم‌گیری، اشتراک و اجتماع شمارش‌پذیر بسته است. ضروری است که مجموعه اصلی $$A$$ و همچنین مجموعه تهی ($$\emptyset$$) نیز در سیگما-جبر حضور داشته باشند.

به طور خلاصه مجموعه‌های بورل در اعداد حقیقی را می‌توان از اجتماع و اشتراک مجموعه‌ها یا فاصله‌های باز و بسته از اعداد حقیقی، تولید کرد. به بیان دیگر اگر $$E_1 , E_2 , \ldots$$ متعلق به کلاس مجموعه‌های بورل $$B$$ باشند، آنگاه $$\cup E_i$$ و $$\cap E_i$$ نیز به $$B$$ تعلق دارند. همچنین $$E'=R-E$$‌ که متمم مجموعه $$E$$ در مجموعه اعداد حقیقی در نظر گرفته می‌شود، نیز در مجموعه $$B$$ ظاهر خواهد شد.

نام‌گذاری چنین مجموعه‌هایی به افتخار ریاضیدان فرانسوی «امیل بورل» (Émile Borel) صورت گرفته است. کارهای عملی و تحقیقات منتشر شده از او در رشد نظریه اندازه و احتمال نقش بسیار مهمی دارد.

تولید جبر بورل

در اینجا فرض می‌کنیم که توپولوژی $$X$$ یک «فضای متریک» (Metric Space) است. ترتیب مراحل ایجاد یک جبر بورل در ادامه شرح داده می‌شود ولی بهتر است ابتدا به منظور یادآوری، مجموعه باز و بسته را معرفی کنیم.

فیلم آموزش مبانی آنالیز حقیقی در فرادرس

کلیک کنید

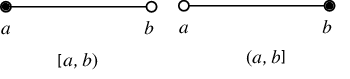
مجموعه باز: مجموعه‌ای که شامل نقاط مرزی همسایگی نباشد، یک مجموعه باز است. این موضوع را به وسیله رابطه همسایگی زیر نشان می‌دهیم.

$$\large \forall x \in A: \exists \delta>0; N_{\delta}(x) \subseteq A$$

مجموعه بسته: مجموعه‌ای که شامل نقاط مرزی همسایگی باشد، یک مجموعه بسته است. به بیان دیگر، مجموعه‌ای که متمم آن یک مجموعه باز باشد، یک مجموعه بسته نامیده می‌شود.

$$ \large A \text{ is closed, if } A' = R- A \text{ is an open set} $$

نکته: واضح است که در اینجا فضای متریک شامل یک متر بوده و می‌توان همسایگی برای یک مجموعه را تعریف کرد.

حال به چگونگی تولید سیگما جبر بورل و تشکیل مجموعه بورل می‌پردازیم. ابتدا گردایه $$T$$ از زیر مجموعه‌های $$T$$ را در نظر بگیرید. در حقیقت $$T$$ شامل زیرمجموعه‌هایی از «مجموعه توانی» (Power Set) فضای متریک $$X$$ است. حال شرایط زیر را برای $$T$$ در نظر داشته باشید.

• همه اجتماع‌های شمارش‌پذیر از عناصر $$T$$ را $$T_{\sigma}$$ بنامید.
• همه اشتراک‌های شمارش‌پذیر از عناصر $$T$$ را $$T_{\delta}$$ در نظر بگیرید.
• فرض کنید تساوی $$T_{\delta \sigma}= (T_{\delta})_{\sigma}$$ برقرار است. یعنی اشتراک همه مجموعه‌های حاصل از $$T_{\delta}$$ با اشتراک‌های اجتماع همه اعضای $$T$$ برابر است.

حال استقرا زیر را روی دنباله $$G^m$$ دنبال می‌کنیم. به این موضوع نیز توجه داشته باشید که $$m$$ یک «عدد ترتیبی» (Ordinal Number) است.

• برای حالت پایه، $$m=0$$ و $$G^0$$ را گردایه حاصل از مجموعه‌های باز $$X$$ محسوب می‌کنیم.
• رابطه زیرا را با توجه به کران انتهایی $$i$$ روی $$G$$ در نظر می‌گیریم.

$$ \large G^{i}=[G^{{i-1}}]_{{\delta \sigma }} $$

• اگر $$i$$ ‌به کران و حد نهایی خود رسید، رابطه را به شکل زیر در نظر خواهیم گرفت.

$$ \large G^{i}=\bigcup _{{j<i}}G^{j}$$

ادعا می‌کنیم که $$G^{\omega_1}$$، جبر بورل است بطوری که $$\omega_1$$ اولین عدد ترتیبی غیرقابل شمارش (first uncountable ordinal number) است. به این ترتیب، جبر بورل را می‌توان از گردایه‌ای از مجموعه‌های باز بوسیله تکرار مراحل گفته شده، تولید کرد. به این ترتیب همگرایی زیر در صورت رسیدن به اولین عدد ترتیبی غیرقابل شمارش حاصل خواهد شد.

$$ \large G\mapsto G_{{\delta \sigma }}$$

نکته: توجه داشته باشید که برای هر مجموعه بورل مثل $$B$$ یک عدد شمارش‌پذیر ترتیبی مثل $$\alpha_{b}$$ وجود دارد که می‌توان براساس آن مجموعه $$B$$ را ساخت. به این منظور به نوشتار عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده مراجعه کنید.

برای اثبات این ادعا، در نظر داشته باشید که هر مجموعه باز از این فضای متریک (متر دار) از اجتماع دنباله‌ای صعودی تشکیل شده است. به این ترتیب متمم مجموعه‌های تصویر شده توسط $$G^m$$ به خودش، برای هر کران عدد ترتیبی مثل $$m$$، نسبت به عمل اجتماع شمارش‌پذیر، بسته است. در ادامه به بعضی از جبرهای بورل اشاره خواهیم کرد.

مثال‌هایی از جبر بورل

یکی از موضوعات بسیار مهم در نظریه احتمال (Theory of Probability)، جبر بورلی است که روی اعداد حقیقی ساخته می‌شود. در مبحث متغیر تصادفی (Random Variable) و با توجه به تکیه‌گاه آن، بیان می‌شود که برای هر مجموعه بورل از اعداد حقیقی، باید بتوان تابعی به صورت معکوس متغیر تصادفی یافت که هر مجموعه بورل را به یک پیشامد در فضای نمونه، نگاشت کند در غیر اینصورت متغیر تصادفی وجود نخواهد داشت. به این معنی که با مشخص بودن متغیر تصادفی با تکیه‌گاه اعداد حقیقی، یک فضای احتمال تعریف می‌شود که در آن توزیع احتمال براساس مجموعه‌های بورل و یک اندازه (Measure) در جبر بورل خواهد بود.

جبر بورل روی اعداد حقیقی، کوچکترین سیگما جبر ($$\sigma \text{-algebra}$$) روی اعداد حقیقی است که شامل همه فاصله‌های باز و بسته است.

با توجه به ویژگی عدد اصلی (Cardinality) مجموعه‌ها، می‌توان نشان داد که تعداد مجموعه‌های بورل کمتر یا مساوی با رابطه زیر است.

$$ \large {\displaystyle \aleph _{1}\cdot 2^{\aleph _{0}}\,=2^{\aleph _{0}}}$$

توجه دارید که $$\aleph_0$$ عدد اصلی مجموعه اعداد طبیعی است. همچنین $$\aleph_1$$ کوچکترین عدد اصلی است که از $$\aleph_0$$ بزرگتر است که آن را عدد اصلی مجموعه اعداد حقیقی می‌شناسیم. به نظر می‌رسد که این رابطه شبیه تعداد اعضای مجموعه توانی یک مجموعه است.

مجموعه‌های غیر بورلی

شاید این طور به نظر برسد که همه زیرمجموعه‌های اعداد حقیقی، مجموعه‌های بورل تشکیل می‌دهند. در حالی که چنین چیزی همیشگی نیست. یکی از مثال‌هایی که در این زمینه ایجاد شده توسط «نیکولای لوسین» (Nikolai Luzin) معرفی شده است که در ادامه به این مثال خواهیم پرداخت.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل مساله در فرادرس

کلیک کنید

توجه داشته باشید که هر عدد گویا (Irrational Number) را می‌توان به صورت دنباله‌ای نامتناهی از مجموع کسرهای به شکل زیر نمایش داد.

$$ \large x=a_{0}+\dfrac{1}{a_{1}+\dfrac{1}{a_{2}+\dfrac{1}{a_{3}+\dfrac {1}{\ddots \,}}}}$$

که در آن $$\alpha_0$$ یک عدد صحیح بوده و بقیه آن‌ها (یعنی $$\alpha_k$$) اعداد صحیح مثبت هستند. مجموعه $$A$$ را همه اعداد گویا در نظر بگیرید که وابسته به دنباله $$(a_0 , a_2 , \ldots )$$ هستند، بطوری که رابطه بخش‌پذیری بینشان برقرار است. به این معنی که هر عنصر از آن توسط عنصر بعدی شمرده (عاد)‌ می‌شود. مجموعه $$A$$، که به صورت بالا تعریف شد، یک مجموعه بورل نیست. البته اثبات آن به دشواری صورت گرفته ولی در کتاب‌های اصلی مربوط به تئوری و نظریه اندازه (+)، مورد بررسی قرار گرفته است.

از طرفی بین مجموعه بورل و مجموعه اندازه‌پذیر لبگ (Lebesgue Measurable) نیز تفاوت‌هایی وجود دارد. می‌توان به کمک یک مثال نشان داد که هر مجموعه اندازه‌پذیر لبگ، لزومی ندارد که یک مجموعه بورل باشد. در حقیقت مجموعه‌های بورلی وجود دارند که اندازه‌پذیر لبگ نیستند. این موضوع را در نوشتارهای بعدی نظریه مجموعه‌ها و نظریه اندازه در مجله فرادرس به شکل گسترده‌تر مورد بررسی قرار خواهیم داد.

خلاصه و جمع‌بندی

در این نوشتار با مجموعه بورل و نقش آن در نظریه اندازه و ریاضیات بخصوص در مباحث مربوط به احتمال و متغیر تصادفی آشنا شدیم. همچنین ویژگی‌های مجموعه‌های بورل نیز مورد بحث قرار گرفت. به کمک مثالی نشان دادیم که ممکن است مجموعه‌ای اندازه‌پذیر لبگ بوده ولی یک مجموعه بورل نباشد. از آنجایی که بحث متغیر تصادفی در آمار و نظریه احتمال بسیار مرتبط با موضوع مجموعه‌های بورل است، برای کسانی که علاقمند به این مباحث هستند، آشنایی با آن از اهمیت زیادی برخوردار است. در نوشتارهای بعدی از سری مطالب ریاضیات در مجله فرادرس، به اندازه بورل (Borel Measure) و ارتباط آن با مجموعه‌های بورل خواهیم پرداخت.