مدلسازی سیستم – به زبان ساده
مدلسازی سیستمهای دینامیکی، مکانیکی و الکتریکی اولین گام در فرایند طراحی کنترلکننده محسوب میشود. در مدلسازی سیستم، تلاش میشود تا یک مدل ریاضی مناسب برای توصیف عملکرد یک سیستم به دست آید و سپس با توجه به آن کنترلکننده را طراحی کرد. در مدلسازی سیستم، مدل ریاضی مربوط به آن را میتوان یا با استفاده از قوانینی فیزیکی (Physical Laws) و یا با استفاده از دادههای تجربی (Experimental Data) به دست آورد. در این مطلب قصد داریم به بیان نمایش تابع انتقال سیستم و نیز نمایش فضای حالت یک سیستم بپردازیم. در هر بخش چند مثال بسیار ساده برای مدلسازی سیستم مکانیکی و الکتریکی را حل میکنیم و در نهایت نحوه ایجاد این مدلها را در نرمافزار متلب نشان میدهیم. مهمترین دستورات متلب که در این مطلب مورد استفاده قرار میگیرند، ss و tf هستند.
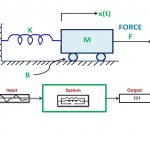
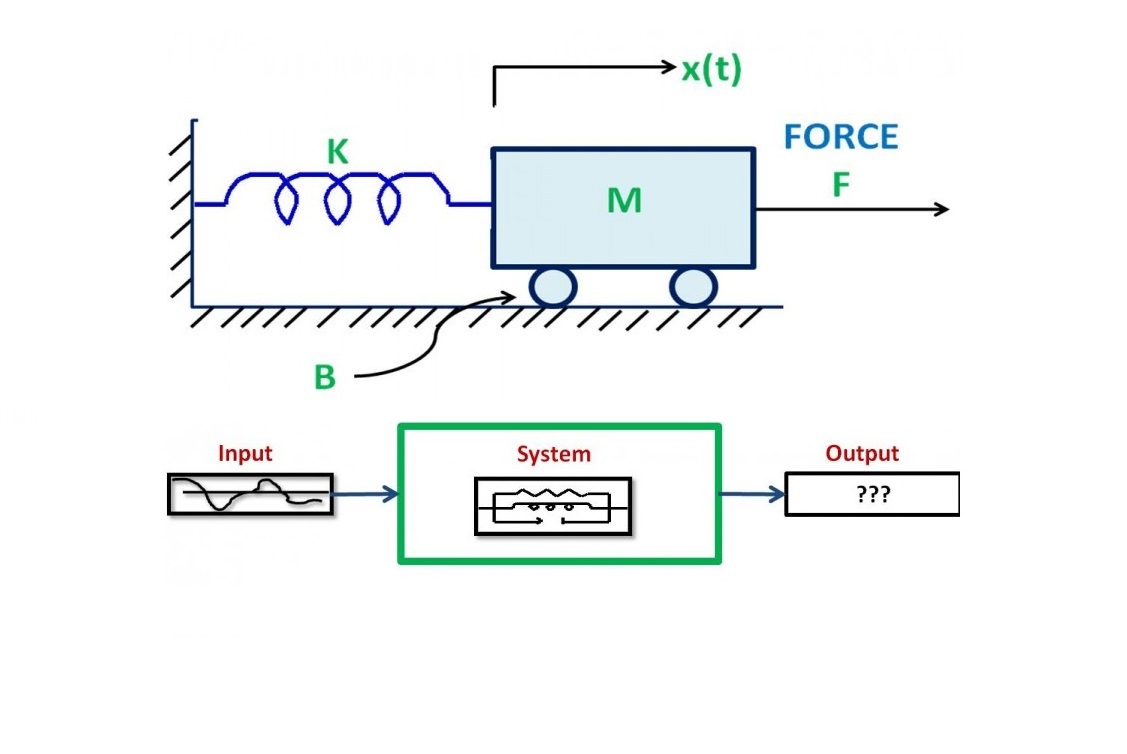
مدلسازی سیستم دینامیکی
سیستمهای دینامیکی سیستمهایی هستند که با گذر زمان و بر اساس یک قانون ثابت، دچار تغییر و یا تکامل میشوند. برای بسیاری از سیستمهای فیزیکی، این قانون میتواند بر اساس مجموعهای از معادلات دیفرانسیل مرتبه اول به صورت زیر بیان شود:
در معادله بالا، بردار حالت نامیده میشود که مجموعهای از متغیرهای تشکیل دهنده دینامیک سیستم در زمان را در خود دارد.
بردار ورودیهای خارجی یا بیرونی سیستم در زمان است و تابعی (شاید غیرخطی) است که مشتق زمانی (نرخ تغییرات) بردار حالت را مشخص میکند.
بردار حالت را در هر زمان آینده میتوان به صورت دقیق تعیین کرد. برای این کار به داشتن مقدار اولیه و ورودیهای گذشته نیاز داریم و با اعمال انتگرال از تا روی معادله بالا مقدار خروجی در هر لحظه به صورت دقیق به دست میآید.
اگرچه متغیرهای حالت، منحصر به فرد نیستند، اما باید تعداد حداقل متغیر وجود داشته باشد که بتوان با آنها حالت سیستم را بررسی و رفتار آینده آن را پیشبینی کرد. ، مرتبه سیستم (System Order) نامیده میشود و بُعد فضای حالت را مشخص میکند. مرتبه سیستم، معمولاً با تعداد عناصر ذخیرهکننده انرژی در سیستم متناظر است.
مدلسازی سیستم با نمایش فضای حالت سیستم
نمایش بلوک دیاگرامی یک سیستم با کنترلکننده فیدبک در شکل زیر نشان داده شده است.
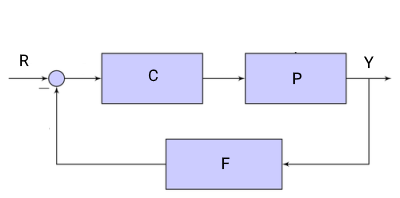
در شکل بالا، مقادیر را میتوان به صورت زیر نامگذاری کرد:
- : ورودی سیستم
- : خروجی سیستم
- : بلوک کنترلی
- یا : بلوک پلنت یا سیستم مورد نظر
- : حلقه فیدبک
در این قسمت میخواهیم یکی از روشهای توصیف دینامیک و مدلسازی سیستم را معرفی کنیم که به مدل فضای حالت (State Space Model) معروف است. قصد داریم با بیان چند مثال، این روش را بیان کنیم.
مثال ۱ از مدلسازی سیستم
سیستم جرم و فنر زیر را در نظر بگیرید.
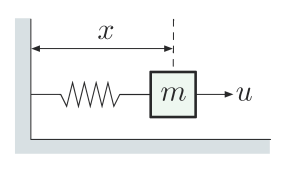
معادله دیفرانسیل توصیف کننده سیستم بالا را به دست آوردید و برای مدلسازی سیستم سپس به فرم ماتریسی بازنویسی کنید.
حل:
برای این کار باید معادلات دیفرانسیل یا ODE را به مجموعهای از معادلات دیفرانسیل درجه یک تبدیل کرد. توجه کنید که متغیر x در این سیستم برابر با جابهجایی فنر از موقعیت اولیه یا در نظر میشود، نه فاصله آن از دیوار؛ زیرا فنر میتواند هم فشرده شود و هم دچار کشش شود.
با توجه به قانون دوم نیوتون، مجموع نیرو برابر با حاصل ضرب جرم در شتاب است. بنابراین در این سیستم داریم:
در فرمول بالا، نیروی برابر با مجموع نیروی فنر و اصطکاک و نیروی خارجی در نظر گرفته میشود. همچنین با استفاده از قانون هوک (Hooke's Law)، نیروی فنر (Spring Force) را به صورت زیر میتوان به دست آورد:
با توجه به قانون استوک (Stokes' Law)، نیروی اصطکاک (Friction Force) برابر است با:
بنابراین در نهایت معادله زیر برای این سیستم به دست میآید:
میتوانیم مقادیر ، و را به یک سمت از معادله منتقل کنیم و متغیر در سمت دیگر از معادله باقی بماند. سپس ضرایب معادله را نرمالیزه میکنیم:
فرمول بالا، یک معادله دیفرانسیل مرتبه دو را در اختیار ما قرار میدهد. با بازنویسی این معادله در فرم کانونی خود، میتوان آن را به مجموعهای از معادلات دیفرانسیل درجه اول تبدیل کرد. متغیر سرعت (Velocity) را برابر با در نظر میگیریم و دستگاه معادلات زیر را به دست میآوریم:
برای مشاهده واضحتر فرم ماتریسی معادله ۱، میتوان آن را به صورت زیر بازنویسی کرد:
در نهایت میتوان معادله را به فرم ماتریسی مانند زیر نوشت:
مثال ۲ از مدلسازی سیستم
مدار RL فرضی مانند شکل زیر را در نظر بگیرید.
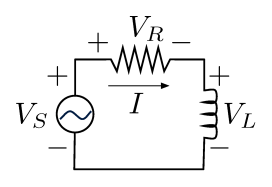
معادله دیفرانسیل متناظر با این سیستم را به دست آورید و سپس با کاهش درجه معادلات دیفرانسیل به مرتبه یک، فرم ماتریسی آن را بنویسید.
حل:
در حالت کلی، نحوه انجام این کار بسیار شبیه به مثال یک است، اما در این شرایط باید از قانون ولتاژ کیرشهف (Kirchhoff’s Voltage Law) استفاده کنیم و جمع جبری افت ولتاژ در طول مدار را برابر با صفر قرار دهیم:
افت ولتاژ در طول مقاومت را میتوان از قانون اهم (Ohm's Law) به دست آورد:
همچنین با اعمال قانون فارادی (Faraday's Law) افت ولتاژ در طول سلف را میتوان به صورت زیر محاسبه کرد:
بنابراین در حالت کلی میتوان نوشت:
پس داریم:
این معادله درجه یک، توصیف کننده سیستم مثال ۲ است. بنابراین با استفاده از فضای حالت، میتوان مدلسازی سیستم الکتریکی و مکانیکی را انجام داد.
مدلسازی سیستم با فضای حالت n بعدی
با توجه به مثالهای ۱ و ۲، برای سیستمی با n حالت (State) و m ورودی (Input) نیز میتوان نوشت:
نمایش فضای حالت خطی، برابر با مجموعهای از معادلات دیفرانسیل در فرم ماتریسی است. پس سیستم را میتوان به صورت زیر در فرم ماتریسی نوشت:
معادله بالا را میتوان به صورت زیر خلاصه کرد:
در نمایش فضای حالت، فرمول بالا را معادله دینامیک (Dynamics Equation) سیستم میگویند. میتوانیم به معادله دینامیک بالا، معادله خروجی را نیز اضافه کنیم. خروجیهای را به صورت بردار نشان میدهیم و داریم:
در این فرمول، برابر با یک ماتریس است. به عنوان مثال، اگر فقط حالت مورد نظر باشد، میتوانیم فقط آن را اندازه بگیریم و بنویسیم:
بنابراین در حالت کلی، نمایش فضای حالت سیستم را میتوان به فرم زیر نوشت:
مدلسازی سیستم بر اساس نمایش فضای حالت، برای انواع مختلف سیستمها مفید و کاربردی است. از مثال متداول پاندول ساده برای توضیح بیشتر کار با مدل فضای حالت استفاده میکنیم.
مثال ۳ از مدلسازی سیستم
یک سیستم پاندول ساده را مطابق شکل زیر در نظر بگیرید.
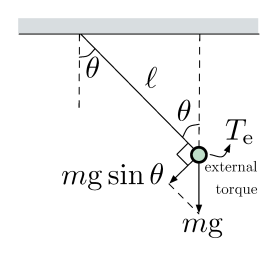
معادلات دیفرانسیل توصیفکننده سیستم را بنویسید و سپس مدل فضای حالت آن را به دست آوردید.
حل
مشابه با مثال یک، در این مثال نیز از قانون دوم نیوتون برای حرکت دورانی (چرخشی) استفاده میکنیم. بر اساس این قانون، مجموع گشتاور برابر با اینرسی لحظهای در شتاب زاویهای است. بنابراین داریم:
در فرمول بالا، گشتاور کلی یا ، برابر با مجموع گشتاور پاندول و گشتاور خارجی است. گشتاور پاندول و اینرسی لحظهای هر کدام به صورت زیر به دست میآیند:
پس از جایگذاری داریم:
$$ \begin{align} \label{d2_eq2}<br /> \ddot{\theta} &= - \frac{{\rm g}}{\ell}\sin \theta + \frac{1}{m\ell^2}T_{\rm e}.<br /> \end{align} $$
فرمول بالا یک معادله غیرخطی است. از ریاضیات پایه به یاد داریم که برای زوایای کوچک میتوان از تقریب استفاده کرد. نمایی از تقریب سینوس زاویه برای زوایای کوچک در تصویر زیر نشان داده شده است.
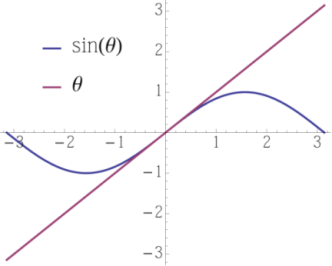
بنابراین داریم:
$$ \begin{align} \label{d2_eq3}<br /> \ddot{\theta} &= - \frac{{\rm g}}{\ell} \theta + \frac{1}{m\ell^2}T_{\rm e}.<br /> \end{align} $$
مطابق آن چه در مثال یک انجام دادیم، در این مثال نیز با معرفی متغیرهای و داریم:
بنابراین نمایش فضای حالت برای یک سیستم پاندول ساده برابر است با:
البته سوالی که ممکن است پیش بیاید این است که اگر زاویه پاندول، زاویه کوچکی نباشد، آنگاه باید به چه صورت عمل کرد. فرض کنید زاویه پاندول در حدود باشد. در این صورت میتوان از تقریب استفاده کرد.
خطی سازی فضای حالت
همان طور که در مثال سوم دیدیم، برای به دست آوردن مدل فضای حالت خطی، از تقریب حول نقطه استفاده کردیم. در این بخش میخواهیم بدانیم که آیا یک استراتژی کلی برای خطی سازی مدل فضای حالت وجود دارد یا خیر.
استفاده از سری تیلور (Taylor Series) یک روش مناسب برای خطی سازی مدل فضای حالت است. بسط سری تیلور برای متغیر حول نقطه ، به صورت زیر نوشته میشود:
برای یک سیستم کنترل غیر خطی در حالت کلی میتوان نوشت:
میتوان بسط سری تیلور را برای چند متغیر نیز اعمال کرد. فرض کنید و یک نقطه تعادل (Equilibrium Point) سیستم باشد، یعنی . به عبارت دیگر، زمانی که سیستم در حال استراحت باشد و هیچ نیروی کنترلی به آن اعمال نشود، سیستم به حرکت در نمیآید.
حول نقطه ، برای هر از که باشد، داریم:
بعد از جمع کردن معادله، حال مدل فضای حالت خطی شده به صورت فرمول زیر به دست میآید.
در معادله بالا، در واقع ژاکوبین نسبت به متغیر است. به طریق مشابه، ژاکوبین نسبت به متغیر در نقطه تعادل سیستم است. نکته مهمی که در اینجا باید به آن توجه کنیم این است که چون از عبارات درجه بالا صرف نظر کردهایم، در نتیجه سیستم خطی به دست آمده تقریبی از سیستم واقعی است و فقط برای تغییرات کوچک حول نقطهٔ تعادل معتبر است.
حال بیاید از استراتژی کلی که در این قسمت به دست آوردیم، برای محاسبه مدل فضای حالت سیستم پاندول مثال ۳ استفاده کنیم.
حل مثال ۳ با روش بسط سری تیلور
میخواهیم مدل فضای حالت سیستم پاندول مثال ۳ را خطی سازی کنیم. مدل فضای حالت اصلی سیستم به صورت زیر نوشته میشود:
معادله را حول نقطه تعادل به صورت زیر خطی سازی میکنیم.
بنابراین مدل فضای حالت خطی شده سیستم پاندول برابر است با:
در نهایت مدلسازی سیستم پاندول به دست میآید. مشاهده میکنیم که معادله به دست آمده با استفاده از روش بسط سری تیلور، مشابه با جواب به دست آمده به روش تقریب زاویه است.
روش عمومی خطی سازی
به این نکته توجه کنید که اگر نقطه تعادل سیستم در نقطهای به غیر از قرار داشته باشد، باید با استفاده از انتقال، نقطه تعادل غیر صفر را به مبدا بازگردانیم. نحوه این انتقال به صورت زیر است:
چون ، سیستمی است که نقطه تعادل آن در مبدا قرار دارد، در نتیجه میتوان از روش بالا برای خطی سازی مدل فضای حالت استفاده کرد. بعد از محاسبه ژاکوبین، میتوان مدل خطی شده را بر حسب متغیرهای و به دست آورد و در نهایت از تغییر متغیر و استفاده کرد تا یک مدل خطی شده بر حسب متغیرهای و به دست آید.
توجه کنید که برای هر سیستم خطی، باید یک نقطه تعادل در وجود داشته باشد؛ زیرا اگر تابع در حال حاضر خطی باشد، آنگاه رابطه زیر برقرار است:
نمایش فضای حالت با عنوان نمایش حوزه زمان نیز شناخته میشود. این نمایش میتواند به سادگی برای سیستمهای چند ورودی - چند خروجی، سیستمهای با شرایط اولیه غیر صفر و نیز سیستمهای غیر خطی مورد استفاده قرار گیرد. نمایش مدل سیستم بر اساس فضای حالت، به صورت گسترده در تئوری کنترل مدرن مورد استفاده قرار میگیرد.
پاسخ ضربه
در بخش قبلی به استفاده از مدل فضای حالت برای مدلسازی سیستم پرداختیم. مدل فضای حالت یک روش موثر برای توصیف سیستم است.
مدل پاسخ ضربه
نترل در یک چارچوب متحد است. همان طور که گفتیم، در حالت کلی مدل فضای حالت یک سیستم را میتوان به صورت زیر نوشت:
که در فرمول بالا داریم:
- : بردار حالتها در زمان t
- : بردار ورودیها در زمان t
- : بردار خروجیها در زمان t
- : ماتریس دینامیکهای سیستم
- : ماتریس کنترل یا ورودی
- : ماتریس خروجی یا سنسور
حال سوالی که پیش میآید، این است که برای مدلسازی سیستم با یک ورودی معین ، چگونه مقدار خروجی را به دست آوریم؟
توجه کنید که ما در این مطلب فقط سیستمهای تک ورودی - تک خروجی (Single-Input, Single-Output) یا SISO را در نظر میگیریم. به عبارت دیگر، برای تمام زمانهای داریم:
در مدل فضای حالت بالا، اگر باشد، آنگاه میتوان گفت که سیستم SISO است.
برای پاسخ به سوال مطرح شده، ابتدا باید پاسخ ضربه سیستم را تعریف کنیم. همان طور که در مطالب قبلی مجله فرادرس اشاره شد، ضربه واحد (Unit Impulse) یا تابع دلتای دیراک (Dirac’s δ-function)، یک تابع از زمان است که در شرایط زیر صدق کند:
- برای تمام زمانهای درست باشد.
- به ازای ، عبارت برقرار باشد.
در تصویر زیر نمایی از تابع دلتای دیراک یا ضربه واحد را مشاهده میکنید.
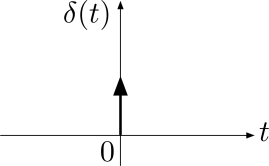
میتوان تابع ضربه واحد را به صورت حدی از ضربه در نظر گرفت که مساحت زیر آن برابر با واحد باشد. این مفهوم در تصویر زیر به خوبی نشان داده شده است. وقتی ، آنگاه ضربه باریکتر میشود ()، اما مساحت زیر منحنی، همان باقی میماند.
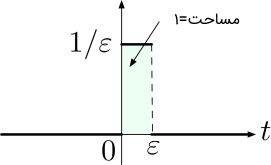 و ارتفاع " width="271" height="165">
و ارتفاع " width="271" height="165">بیان خروجی سیستم به صورت انتگرال کانولوشن
حال ورودی را در نظر بگیرید. این تابع در واقع بیانگر ضربه واحد در زمان است. اگر یک سیستم خطی و نامتغیر با زمان (Time-Invariant) یا LTI مانند تصویر زیر را در نظر بگیریم که شرایط اولیه این سیستم صفر باشد، آنگاه میتوان گفت که خروجی سیستم برابر با خواهد بود. در این حالت، تابع را پاسخ ضربه سیستم میگویند.
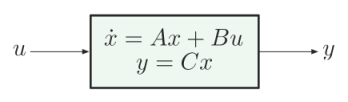
با در اختیار داشتن پاسخ ضربه یک سیستم، میتوان پاسخ آن سیستم به هر ورودی دلخواه دیگر را نیز به دست آورد. در حقیقت، با توجه به خاصیت انتقالی (Sifting Property) تابع ضربه، در برای هر تابع که خوش رفتار (Well-Behaved) باشد، داریم:
معادله بالا بیان میکند که تابع ضربه واحد قادر است مقدار تابع را به منتقل کند. بنابراین هر تابع منظم منطقی (Reasonably Regular) را میتوان به صورت انتگرال توابع ضربه واحد بیان کرد. برای محاسبه پاسخ سیستم به سایر ورودیهای تصادفی با استفاده از پاسخ ضربه ، میتوان با استفاده از خاصیت انتقالی بالا، سیگنال ورودی را به فرم انتگرالی نوشت:
برای تمام سیستمهای خطی، پاسخ کلی سیستم که در اثر دو یا چند ورودی به وجود میآید، برابر با جمع جبری پاسخ سیستم به هر ورودی تکی است. این اصل را اصل جمع آثار میگویند.
در نتیجه، با استفاده از اصل جمع آثار (Superposition)، پاسخ یک سیستم خطی به مجموع یا انتگرال ورودیها برابر با جمع یا انتگرال پاسخ سیستم به تک تک ورودیها است. در نتیجه میتوان نوشت:
انتگرال در معادله بالا که مقدار را تعیین میکند، کانولوشن و نام دارد. بنابراین در یک سیستم LTI با شرایط اولیه صفر، مقدار خروجی برابر با کانولوشن ورودی و پاسخ ضربه سیستم است. پس داریم:
اما متاسفانه فرمول بالا راه راحتی برای محاسبه مقدار خروجی با در اختیار داشتن ورودی نیست. راه حل دیگری که در عمل بسیار مورد استفاده قرار میگیرد، استفاده از تبدیل لاپلاس (Laplace Transform) است.
مدلسازی سیستم با تبدیل لاپلاس و تابع انتقال
در این قسمت میخواهیم برای مدلسازی سیستم از روش تابع انتقال استفاده کنیم. میدانیم که تبدیل لاپلاس دو طرفه تابع را میتوان به صورت زیر محاسبه کرد:
$$ \begin{align*} \tag{Laplace} \label{d3_lt}<br /> F(s) = \int^\infty_{-\infty} f(\tau)e^{-s\tau}d\tau,<br /> \end{align*} $$
در فرمول بالا، و یک متغیر مختلط است. مقادیر سیستم در حوزه زمان و نیز در حوزه فرکانس به صورت زیر هستند:
| حوزه فرکانس | حوزه زمان |
کانولوشن در حوزه زمان به صورت است، در حالی که با گرفتن تبدیل لاپلاس از طرفین معادله بالا، میتوان نوشت:
در نتیجه مقدار خروجی در حوزه فرکانس، که معادل با مقدار کانولوشن بیان شده در قسمت قبل است، به صورت زیر نوشته میشود:
همچنین تبدیل لاپلاس پاسخ ضربه سیستم را میتوان به صورت زیر محاسبه کرد:
تابع به دست آمده در معادله بالا را تابع انتقال (Transfer Function) سیستم میگویند. تابع انتقال سیستم نیز یک راه مفید برای مدلسازی سیستم است.
همان طور که گفتیم سیستمهای LTI دارای یک مشخصه بسیار مهم هستند که بر اساس آن، اگر ورودی سیستم یک سیگنال سینوسی باشد، مقدار خروجی سیستم نیز یک سیگنالی سینوسی خواهد بود که فرکانس آن با فرکانس سیگنال ورودی برابر است و فقط مقدار دامنه و فاز آنها با یکدیگر متفاوت خواهد بود. اختلاف دامنه و فاز در این دو سیگنال، تابعی از فرکانس است و بر اساس پاسخ فرکانسی سیستم به دست میآیند.
با استفاده از تبدیل لاپلاس، میتوان نمایش حوزه زمان یا نمایش فضای حالت را به نمایش حوزه فرکانس و یا تابع تبدیل سیستم تبدیل کرد. این نمایش بر اساس ورودیها و خروجیهای سیستم است و تابع انتقال نام دارد. یکی دیگر از مزیتهای استفاده از تابع انتقال برای نمایش مدل یک سیستم یا مدلسازس سیستم این است که معادلات دیفرانسیل توصیف کننده سیستم را به معادلات جبری تبدیل میکند که انجام محاسبات و نیز آنالیز با استفاده از آنها بسیار سادهتر است.
اگر سیستم را علّی (Causal) فرض کنیم، در آن صورت خروجیها در زمان از ورودیهای زمان آینده یا تاثیر نخواهند پذیرفت. در چنین سیستمی اگر پاسخ ضربه سیستم در زمان به ورودی ضربه واحد در زمان ۰ باشد، آنگاه مقدار تابع پاسخ ضربه برای برابر با صفر خواهد بود. ما تمام ورودیهای دیگر را نیز مانند تابع ضربه واحد در برابر با صفر فرض میکنیم. در این حالت میتوانیم از تبدیل لاپلاس یک طرفه (One-Sided Laplace Transforms) استفاده کنیم و بنویسیم:
محاسبه تابع انتقال سیستم
در این قسمت میخواهیم به پرسش دیگری پاسخ دهیم. با داشتن ، میتوانیم تبدیل لاپلاس آن را توسط نرمافزار متلب و یا با جدول تبدیل لاپلاس به دست آوریم. اما در مورد و چگونه باید عمل کرد؟ سیستم LTI نشان داده شده در قسمتهای قبل را به یاد بیاورید.
در این سیستم، میتوانیم از فرمول زیر استفاده کنیم و مقدار تابع انتقال سیستم و تابع ضربه آن را به دست آوریم.
حال میخواهیم چند مثال برای مدلسازی سیستم از طریق محاسبه تابع انتقال سیستم را بررسی کنیم.
مثال 1
دینامیکهای سیستم زیر را در نظر بگیرید:
برای مدلسازی سیستم، تابع انتقال سیستم را محاسبه کنید.
حل:
با داشتن ، ما S را به صورت یک عدد ثابت در نظر میگیریم. بنابراین داریم:
حال با جایگذاری مقدار زیر:
در معادله داریم:
$$\begin{align*}\require{cancel}<br /> sH(s)\cancel{e^{st}} &= -a H(s)\cancel{e^{st}} + \cancel{e^{st}}, \qquad \forall~ s, t > 0 \\<br /> sH(s) &= -a H(s) + 1 .<br /> \end{align*} \;\;\;\;\;\; (3) $$
اکنون با محاسبه کردن در فرمول بالا داریم:
اگر به سمت راست تابع انتقال بالا نگاه کنیم، آنگاه مقدار تابع ضربه سیستم نیز با استفاده از جدول و یا گرفتن تبدیل لاپلاس معکوس به صورت زیر به دست خواهد آمد:
این مثال را با استفاده از دیاگرام زیر میتوان نشان داد.
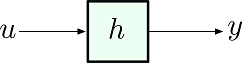
در نتیجه میتوان نوشت:
مدلسازی سیستم با محاسبه پاسخ فرکانسی
تا این قسمت با نحوه محاسبه برای یک ورودی و پاسخ ضربه مشخص آشنا شدیم. در این قسمت میخواهیم با روش مدلسازی سیستم به کمک پاسخ فرکانسی آشنا شویم.
با داشتن ورودی در مثال یک و به ازای تمام مقادیر میخواهیم نسبت زیر را محاسبه کنیم:
برای محاسبه ، باید مطابق نمودار تصویر زیر مراحل را به ازای هر مقدار S که ضروری است، تکرار کنیم.
 " width="528" height="63">
" width="528" height="63">مشکل اصلی این روش در آن است که تابع اگر باشد، به سرعت افزایش مییابد و اگر باشد، به سرعت به سمت صفر کاهش مییابد. در نتیجه، سیگنالهای ورودی باید سیگنالهایی پایدار (Sustained) و محدود (Bounded) باشند. به همین دلیل است که در معادله تبدیل لاپلاس که در بالا معرفی کردیم، S مجاز است که یک عدد مختلط () باشد.
میتوان یک عدد مختلط به فرم را به صورت زیر رسم کرد.
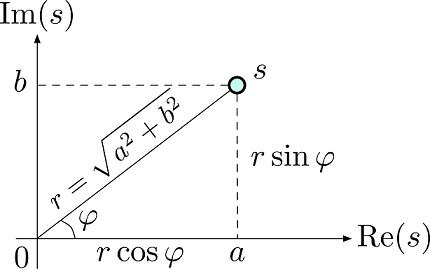
در این حالت، a برابر با قسمت حقیقی و b برابر با قسمت موهومی عدد است. همچنین میتوان از فرم قطبی اعداد مختلط نیز استفاده کرد. در این صورت داریم:
همچنین بر اساس فرمول اویلر داریم:
سیستم LTI با شرایط اولیه صفر را در نظر بگیرید. به این سیستم یک سیگنال ورودی سینوسی با دامنه A و فرکانس رادیان بر ثانیه داده میشود. حال میتوانیم مقدار خروجی را محاسبه کنیم. میدانیم که تابع کسینوس مختلط در به صورت زیر تعریف میشود:
این معادله بر اساس فرمول اویلر نیز درست است. بنابراین، به طریق خطی پاسخ برابر است با:
که در این فرمول داریم:
توجه کنید که یک تابع با مقدار حقیقی و است. میتوان نوشت:
چون هر دو تابع بالا در حوزه اعداد مختلط هستند، بنابراین اگر معادله را با داشتن دامنه و فاز و بازنویسی کنیم، آنگاه داریم:
معادله بالا بیان میکند که پاسخ حالت پایدار یک سیستم به سیگنال کسینوسی با دامنه A و فرکانس ، باز هم یک سیگنال کسینوسی خواهد بود، با این تفاوت که دامنه آن به مقدار مقیاس میشود و فرکانس سیگنال خروجی ثابت باقی میماند، اما فاز آن به شیفت مییابد. در حالت کلی میتوان گفت که پاسخ سیستم به یک سیگنال (نه فقط یک سیگنال سینوسی) همیشه بر طبق محاسبه میشود. برای یک سیستم با شرایط اولیه غیرصفر، پاسخ سیستم به صورت مجموع پاسخ حالت گذرا (Transient Response) و پاسخ حالت پایدار (Steady State Response) توصیف میشود.
مدل فضای حالت در نرمافزار متلب
سیستم جرم و فنر و دمپر زیر را در نظر بگیرید.
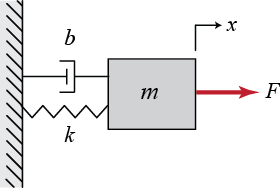
دیاگرام نیروها در سیستم جرم و فنر و دمپر نیز در تصویر زیر نشان داده شده است.
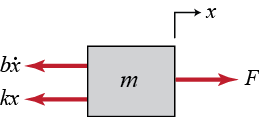
برای مدلسازی سیستم مدل فضای حالت این سیستم به صورت زیر نوشته خواهد شد:
حال میخواهیم نشان دهیم که مدل فضای حالت بالا را چگونه در m-file نرمافزار متلب وارد کنیم.
ابتدا مقادیر زیر را به هر یک از المانهای سیستم اختصاص میدهیم.
| جرم | m | |
| ثابت فنر | k | |
| ثابت میرایی | b | |
| نیروی ورودی | F |
یک m-file جدید در متلب باز میکنیم و دستورات زیر را در آن وارد میکنیم.
sys =
A =
x1 x2
x1 0 1
x2 -1 -0.2
B =
u1
x1 0
x2 1
C =
x1 x2
y1 1 0
D =
u1
y1 0
Continuous-time state-space model.
در نتیجه توانستیم مدلسازی سیستم با استفاده از فضای حالت را در نرمافزار متلب ایجاد کنیم.
وارد کردن تابع انتقال در متلب
تبدیل لاپلاس یک سیستم با شرایط اولیه برابر است با:
بنابراین تابع انتقال از نیروی ورودی به جابهجایی به صورت زیر به دست میآید:
حال برای وارد کردن تابع انتقال یک سیستم در m-file متلب، باید قطعه کد زیر را در فایلی که پارامترهای سیستم در آن تعریف شدهاند، نوشت.
sys =
1
---------------
s^2 + 0.2 s + 1
Continuous-time transfer function.
البته میتوان برای تعریف کردن تابع انتقال و مدلسازی سیستم در متلب و یا سیمیولینک، از روش زیر نیز استفاده کرد.
sys =
1
---------------
s^2 + 0.2 s + 1
Continuous-time transfer function.
در این مطلب به بیان روشهای مختلف مدلسازی سیستم پرداختیم و در نهایت دو مدل را در نرم افزار متلب وارد کردیم. اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش سیستمهای کنترل خطی
- مجموعه آموزشهای مهندسی کنترل
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- فیدبک (Feedback) در سیستم های کنترل — مفاهیم اصلی
- تبدیل z — به زبان ساده
- مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده
^^












