قضیه جمع آثار در مدار – از صفر تا صد (+ دانلود فیلم آموزش رایگان)

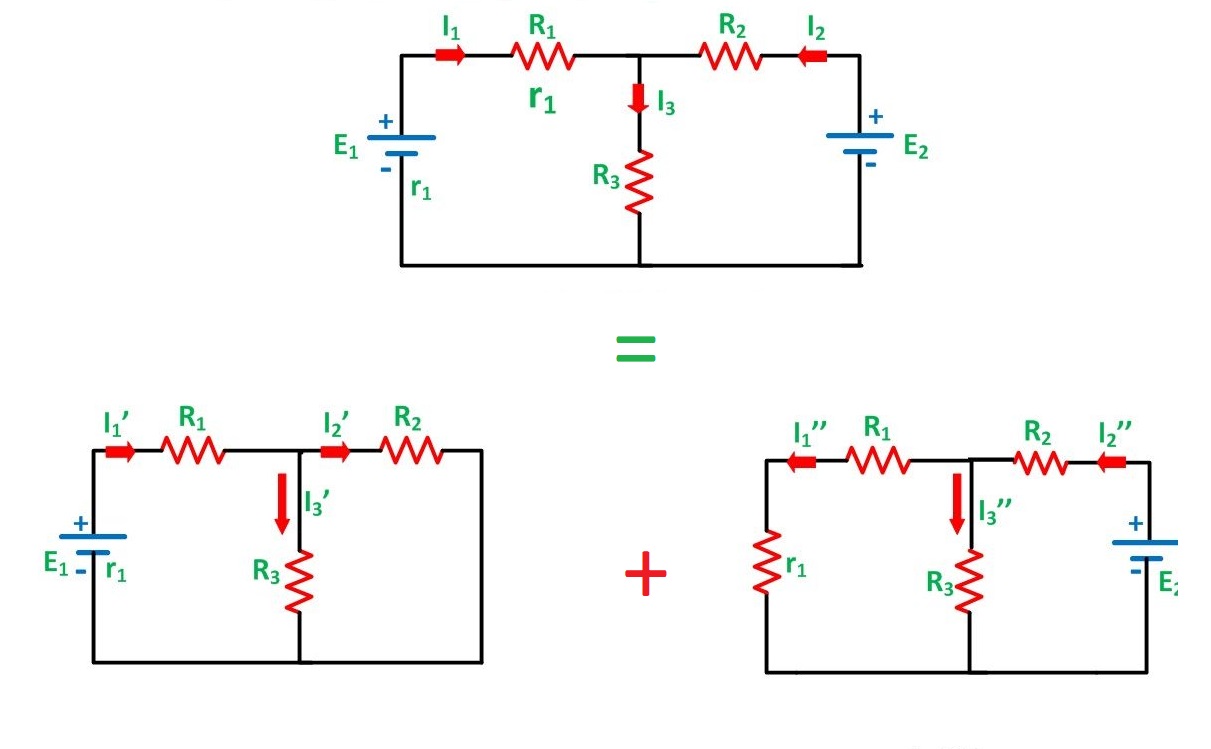
اگر یک مدار دو یا تعداد بیشتری منبع مستقل داشته باشد، یک راه برای تعیین مقدار یک متغیر خاص (ولتاژ یا جریان)، استفاده از تحلیل گره و تحلیل مش است. اما راه دیگری نیز وجود دارد و آن تعیین سهم هر منبع مستقل در یک متغیر و سپس جمع کردن آن‌ها است. این روش به قضیه جمع آثار (Superposition) معروف است. در این مطلب قصد داریم که به بیان این قضیه بپردازیم. قضیه جمع آثار فقط به آنالیز مدارات محدود نیست و در بسیاری رشته‌ها که علت و معلول رابطه خطی با یکدیگر دارند، قابل اعمال است.

بیان قضیه جمع آثار

اساس قضیه جمع آثار بر مشخصه خطی بودن استوار است. قضیه جمع آثار بیان می‌کند که ولتاژ یا جریان در المانی از یک مدار خطی برابر با جمع جبری ولتاژ یا جریان آن المان است که از عملکرد هر کدام از منابع به تنهایی ناشی شده باشد.

اصل جمع آثار از طریق محاسبه تاثیر هر کدام از منابع به صورت جداگانه به ما کمک می‌کند تا اقدام به آنالیز یک مدار با بیش از یک منبع مستقل کنیم. اما برای اعمال قضیه جمع آثار باید به دو نکته توجه کنیم.

1. باید در هر زمان فقط یکی از منابع مستقل روشن باشد و بقیه منابع را خاموش فرض کنیم. برای خاموش کردن منابع ولتاژ را صفر ولت (اتصال کوتاه) و منابع جریان را برابر با صفر آمپر (مدار باز) در نظر می‌گیریم. در این صورت مدار حاصل بسیار ساده‌تر قابل تجزیه و تحلیل است.
2. منابع وابسته باید دست نخورده باقی بمانند؛ زیرا توسط متغیرهای مدار کنترل می‌شوند.

حال قضیه جمع آثار را می‌توان در سه گام اعمال کرد.

1. تمام منابع مستقل به غیر از یکی از آن‌ها را خاموش و ولتاژها و جریان‌های ناشی از منبع باقی مانده را با استفاده از تکنیک‌های آنالیز مش و آنالیز گره محاسبه می‌کنیم.
2. گام اول را برای سایر منابع مدار نیز تکرار می‌کنیم.
3. مقدار کلی را با استفاده از جمع جبری آثار ناشی از تمام منابع مستقل به دست می‌آوریم.

اما آنالیز مدار با استفاده از قضیه جمع آثار یک عیب بزرگ دارد. در اکثر موارد تحلیل مدار با استفاده از این روش ممکن است، زمان بیشتری طول بکشد. اگر مدار شامل سه منبع مستقل باشد، باید سه مدار ساده‌تر را هر بار برای محاسبه اثر یکی از منابع مستقل، آنالیز کنیم. با این حال قضیه جمع آثار در کاستن از پیچیدگی تحلیل یک مدار و تبدیل آن به مداری ساده‌تر، از طریق مدار باز کردن منابع جریان مستقل و اتصال کوتاه کردن منابع ولتاژ مستقل، بسیار مفید است.

لازم است به این نکته توجه کنیم که قضیه جمع آثار برای مدارات با مشخصه خطی صادق است و به همین دلیل برای محاسبه توان ناشی از هر منبع قابل اعمال نیست؛ زیرا توان جذب شده توسط مثلا یک مقاومت به مربع جریان یا ولتاژ بستگی دارد. اگر به محاسبه توان یک المان نیاز داشته باشیم، باید ابتدا ولتاژ یا جریان آن المان را از طریق قضیه جمع آثار محاسبه کنیم.

مثال ۱

با استفاده از قضیه جمع آثار، مقدار ولتاژ $$v$$ را در مدار زیر به دست بیاورید.

فیلم آموزش مبانی مهندسی برق 1 در فرادرس

کلیک کنید

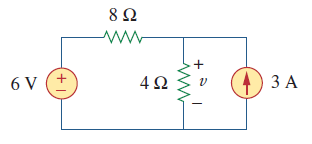
مقدار ولتاژ ناشی از منبع ولتاژ ۶ ولت و منبع جریان ۳ آمپر را به ترتیب  $$v_1$$ و $$v_2$$ نام‌گذاری می‌کنیم. بنابراین ولتاژ $$v$$ به صورت زیر است:

$$v = v_1 + v_2$$

برای محاسبه $$v_1$$، باید منبع جریان را مانند شکل زیر مدار باز فرض کنیم.

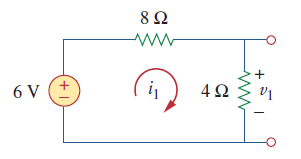
حال از طریق اعمال KCL در حلقه، مقدار جریان برابر است با:

$$12 i_1 -6=0 \rightarrow i_1=0.5A$$

حال ولتاژ $$V_1$$ را به دست می‌آوریم.

$$v_1 = 4 i_1 = 2V$$

برای محاسبه ولتاژ $$V_2$$ باید منبع ولتاژ را مانند شکل زیر اتصال کوتاه فرض کنیم.

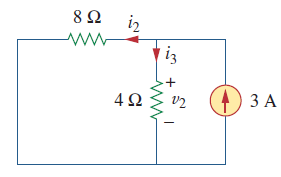
با استفاده از تقسیم جریان داریم:

$$i_{3}=\frac{8}{4+8}(3)=2 \mathrm{A}$$

مقدار $$V_2$$ را می‌توان به صورت زیر محاسبه کرد:

$$V_2 = 4 I_3 = 8 v$$

حال ولتاژ کلی $$V$$ را می‌توان به صورت زیر به دست آورد:

$$v = v_1 + v_2 = 2+8=10$$

مثال 2

در مدار شکل زیر مقدار جریان $$i_o$$ را با استفاده از قضیه جمع آثار بیابید.

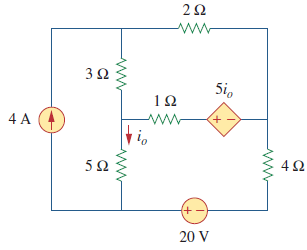
مدار شامل یک منبع وابسته است که باید دست نخورده باقی بماند. در نتیجه داریم:

$$i_o = i_o^\prime + i_o^{\prime \prime}$$

که در آن $$i_o^\prime$$ و $$i_o^{\prime \prime}$$ به ترتیب جریان ناشی از منبع جریان ۴ آمپری و منبع ولتاژ ۲۰ ولتی به صورت جداگانه هستند. برای محاسبه $$i_o^\prime$$، باید منبع ولتاژ مستقل را مانند شکل زیر اتصال کوتاه کنیم.

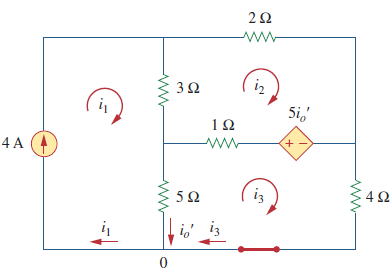
در نتیجه از طریق اعمال آنالیز مش در حلقه شماره ۱ و حلقه شماره ۲ معادلات زیر به دست می‌آیند:

$$i_1 = 4 A$$

$$-3 i_1 +6i_2 -i_3 -5i_o^ \prime = 0$$

برای حلقه شماره ۳ نیز داریم:

$$-5 i_1 -1i_2 +10i_3 +5i_o^ \prime = 0$$

در گره شماره ۰ رابطه زیر برقرار است:

$$i_3 = i_1 - i_o^ \prime = 4 - i_o^ \prime$$

با استفاده از معادلات بالا دستگاه معادلات زیر را به دست می‌آوریم:

$$3 i_{2}-2 i_{o}^{\prime}=8$$

$$i_{2}+5 i_{o}^{\prime}=20$$

برای به دست آوردن مقدار جریان $$i_o^ \prime$$، باید دستگاه معادلات بالا را حل کرد. در نتیجه جواب به صورت زیر است:

$$i_o^ \prime = \frac{52} {17} A$$

حال برای یافتن جریان $$i_o ^ {\prime \prime}$$، منبع جریان ۴ آمپری را مانند شکل زیر مدار باز فرض می‌کنیم.

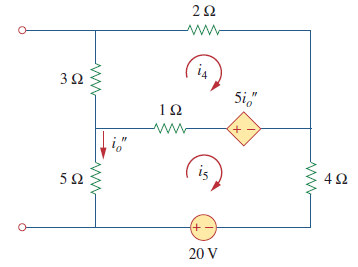
سپس در حلقه ۴ از KVL استفاده می‌کنیم.

$$6 i_{4}-i_{5}-5 i_{o}^{\prime \prime}=0$$

و نیز در حلقه ۵ داریم:

$$-i_{4}+10 i_{5}-20+5 i_{o}^{\prime \prime}=0$$

پس از جایگزینی $$i_5= - i_o ^{\prime \prime }$$ در معادلات بالا، آن‌ها را بازنویسی می‌کنیم.

$$6 i_{4}-4 i_{o}^{\prime \prime}=0$$

$$i_{4}+5 i_{o}^{\prime \prime}=-20$$

مقدار جریان $$i_o^ { \prime \prime }$$ به صورت زیر است:

$$i_{o}^{\prime \prime}=-\frac{60}{17} \mathrm{A}$$

 در نتیجه جریان $$i_o$$ که برابر با مجموع $$i_o ^\prime$$ و $$i_{o}^{\prime \prime}$$ است، به دست می‌آید.

$$i_{o}=-\frac{8}{17}=-0.4706 \mathrm{A}$$

اگر مطالب بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط با آن بیشتر بدانید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• مجموعه آموزش‌های مهندسی برق
• آموزش مدارهای الکتریکی ۱
• مجموعه آموزش‌‌های مهندسی الکترونیک
• آموزش مدارهای الکتریکی ۱ (مرور و حل تست)
• قضیه هم پاسخی — به زبان ساده
• قضیه نورتن (Nortons Theorem) — مفاهیم اصلی
• قضیه تونن (Thevenin’s Theorem) — مفاهیم کلیدی

^^