پاسخ گذرا (Transient Response) — به زبان ساده (+ دانلود فیلم آموزش رایگان)

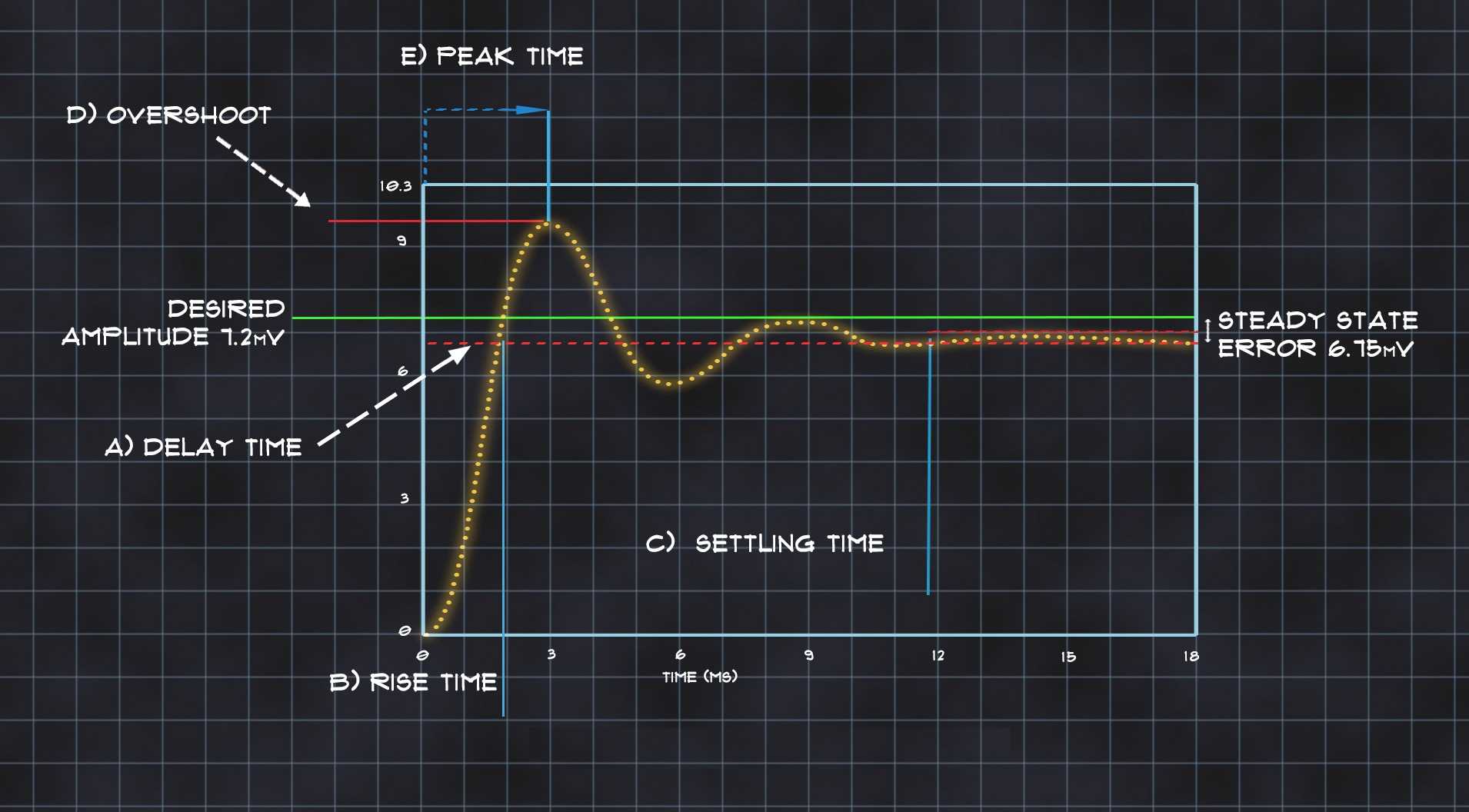
«پاسخ گذرا» (Transient Response) که با نام پاسخ طبیعی نیز شناخته می‌شود، پاسخ یک سیستم دینامیکی به هرگونه تغییرات در حالت ماندگار یا وضعیت تعادل است. پاسخ پله و ضربه، مثال‌هایی از این پاسخ هستند.

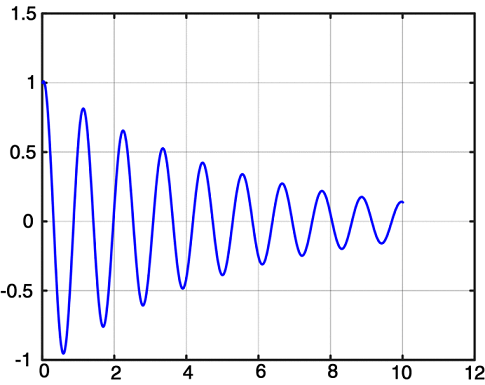
شکل زیر، یک نوسان میرا را نشان می‌دهد که نمونه‌ای از یک پاسخ حالت گذرا است.

خروجی سیستمی با تابع تبدیل $$G(s)$$ و ورودی $$R(s)$$، به صورت زیر است:

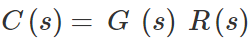
خروجی $$C(s)$$‌ و پاسخ $$c(t)$$ آن را می‌توان به فرم  زیر نوشت که در آن، قطب‌های متمایز $$(p_1,...,p_n)$$ مختلط یا حقیقی هستند.

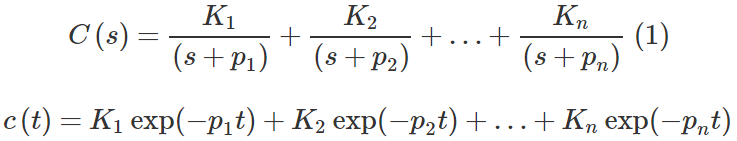
مخرج $$C(s)=G(s)R(s)$$ و بسط کسری جزئی آن، شامل جملاتی از قطب‌های ورودی $$R(s)$$ و سیستم $$G(s)$$ است.

پایداری سیستم

«پایداری» (Stability)، مهم‌ترین مشخصه پاسخ گذرا است. یک سیستم پایدار است، اگر پاسخ حالت گذرای آن کاهشی باشد.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

قضیه پایداری اساسی را می‌توان با کمک رابطه (۱) بیان کرد. اگر هر قطب $$p_i$$ سیستم، مثبت باشد یا بخش حقیقی آن مثبت باشد، نمایی متناظر با آن رشد خواهد کرد و سیستم ناپایدار خواهد بود. بخش حقیقی مثبت بدین معنی است که قطب، در سمت راست محور موهومی صفحه s قرار دارد. بنابراین:

یک سیستم، پایدار است اگر و تنها اگر، همه قطب‌های آن، در سمت چپ محور موهومی صفحه s باشند.

پاسخ گذرای سیستم مرتبه اول

سیستم مرتبه اول زیر، یک مثال متداول برای تحلیل سیستم‌های کنترل است.

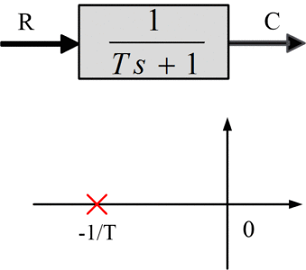
برای یک ورودی پله‌ای $$R(s)=1/s$$، داریم:

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

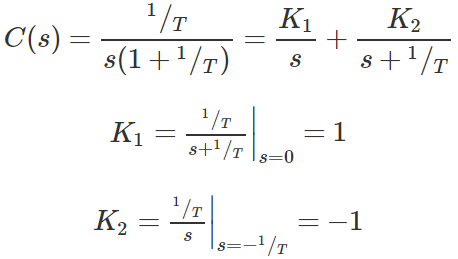
در نتیجه، پاسخ حالت گذرا به فرم زیر است:

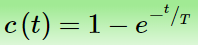
در پاسخ کامل بالا، جمله نخست پاسخ اجباری به ورودی را مشخص می‌کند، در حالی که جمله دوم، پاسخ گذرای ناشی از قطب سیستم است. شکل 3، این پاسخ گذرا (جمله دوم) و $$c(t)$$‌ را نشان می‌دهد. از شکل 3 (الف) واضح است که پاسخ گذرا به صورت نمایی کاهش می‌یابد و از جایی به بعد سرعت کاهش آن کم می‌شود. سرعت این کاهش معمولاً با «ثابت زمانی» (Time constant) یا T اندازه‌گیری می‌شود.

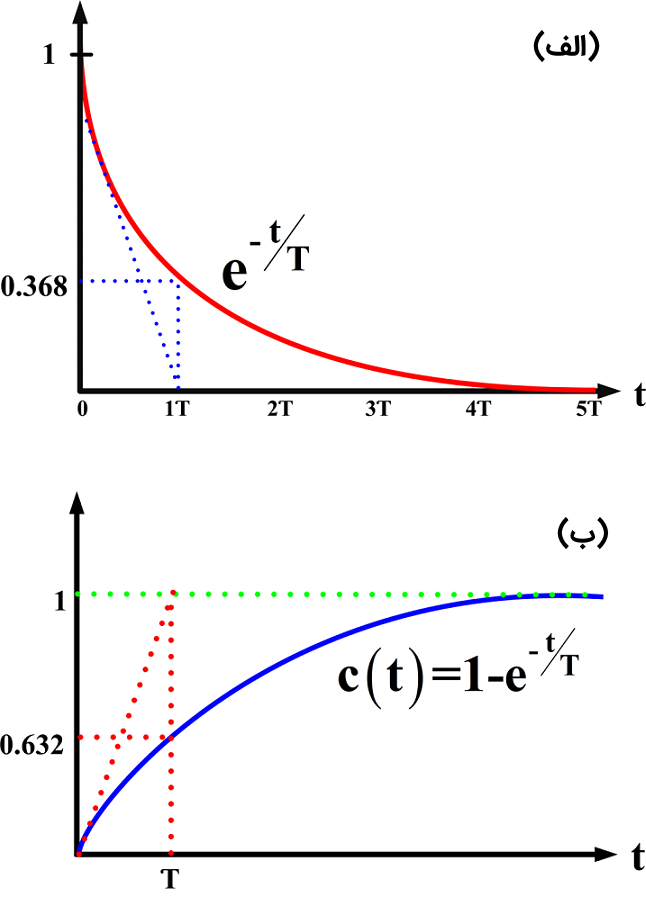
ثابت زمانی یک سیستم، مدت زمانی است که طول می‌کشد پاسخ سیستم به صورت نمایی به اندازه $$e^{-1}=0.368$$ نسبت به مقدار اولیه کاهش یابد. از آن‌جایی که وقتی $$t=T$$، $$e^{-t/T}=e^{-1}$$  است، داریم:

1. ثابت زمانی یک شبکه پس‌فاز $$(1/Ts+1)$$، برابر T ثانیه است.
2. به دلیل همین ثابت زمانی است که سیستم مرتبه اول را به فرم خاصی می‌نویسیم. ضریب s سرعت کاهش پاسخ را نشان می‌دهد.
3. معمولاً با گذشت $$4T$$ ثانیه، پاسخ گذرا به $$1.8 \%$$ مقدار اولیه‌اش کاهش پیدا می‌کند.
4. در $$t=T$$، داریم:‌$$c(T)=1-0.368=0.632$$.

مقادیر متناظر با زمان $$t=T$$، در شکل‌های بالا مشخص شده است. شیب اولیه منحنی‌های بالا نیز با نقطه‌چین مشخص شده است. رابطه زیر، نحوه به دست آوردن T‌ را از شیب نشان می‌دهد:

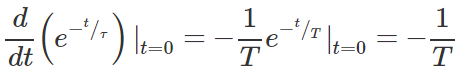
بنابراین، برای یکی سیستم مرتبه اول ساده، دو مشخصه بسیار مهم وجود دارد:

1. پایداری: همان‌گونه که گفته شد، برای آنکه سیستم پایدار باشد، باید قطب $$-1/T$$ در سمت چپ محور موهومی صفحه s باشد. در غیر این صورت، پاسخ گذرای $$e^{-t/T}$$ به جای کاهش، افزایش می‌یابد.

2. سرعت پاسخ: برای آنکه سرعت پاسخ را با کاهش ثابت زمانی افزایش دهیم، قطب $$-1/T$$ باید بزرگتر باشد (در سمت چپ محور موهومی بوده و فاصله زیادی از آن داشته باشد).

پاسخ گذرای سیستم مرتبه دوم

تابع تبدیل متداولی که با آن‌ یک سیستم مرتبه دوم را نشان می دهیم، به صورت استاندارد زیر است:

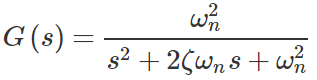
که در آن، $$\omega _n$$ فرکانس طبیعی نامیرا و $$\zeta$$ ضریب میرایی است.

برای ورودی پله $$R(s)=1/s$$، خروجی به صورت زیر خواهد بود:

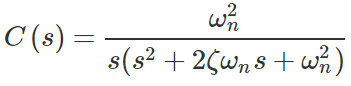
معادله مشخصه به فرم زیر است:

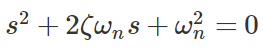
قطب‌های سیستم، به مقدار $$\zeta$$ بستگی دارند:

• اگر $$\zeta >1$$ باشد، $$s_{1,2}=-\zeta \omega_n \pm \omega _n\sqrt{\zeta ^2-1}$$ بوده و پاسخ فرامیرا است.
• اگر $$\zeta =1$$‌ باشد، $$s_{1,2}=-\omega _n$$ بوده و پاسخ میرای بحرانی است.
• اگر $$\zeta <1$$ باشد، $$s_{1,2}=-\zeta \omega_n \pm j \omega _n\sqrt{1-\zeta ^2}$$ بوده و پاسخ فرومیرا است.

شکل 4، صفحه s‌ و موقعیت قطب‌ها را در آن، نشان می‌دهد.

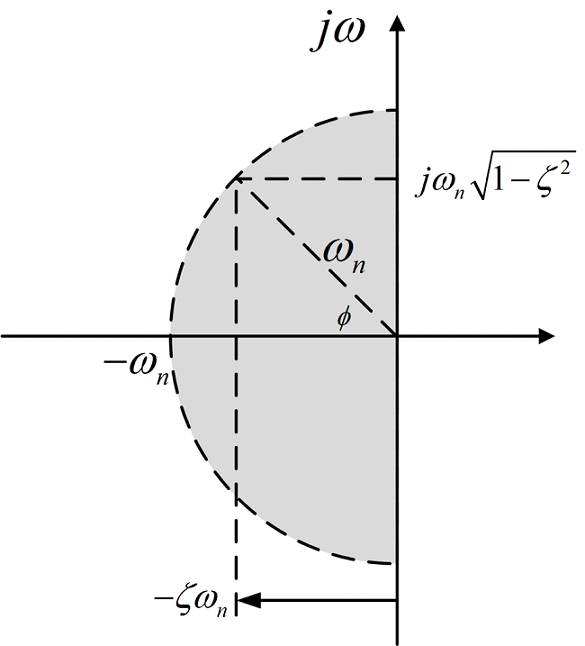
• اگر $$\zeta >1$$، قطب‌ها در قسمت منفی محور حقیقی و دو سمت $$-\omega _n$$‌ هستند.
• اگر $$\zeta =1$$، در قطب در $$-\omega _n$$‌ قرار دارند.
• اگر $$\zeta <1$$، قطب‌ها روی دایره‌ای به شعاع $$\omega _n$$‌ و به مرکز مبدا قرار دارند. فرمول زیر، نحوه به دست آوردن فاصله از مبدا را نشان می‌دهد:

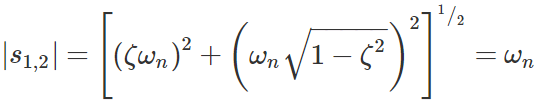
با دقت در شکل ۳، می‌توان نوشت:

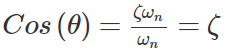
بنابراین،

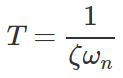
مشابه سیستم مرتبه اول، دامنه پاسخ، با گذشت $$4T$$ ثانیه، به $$2\%$$ مقدار اولیه خود می‌رسد. تعیین رابطه بین رفتار دینامیکی و موقعیت قطب‌ها در صفحه s شکل 4 امری ضروری است:

1. پایداری مطلق: برای کاهش پاسخ گذرا، بخش حقیقی $$-\zeta\omega _n$$ قطب‌ها باید منفی باشد (در سمت چپ محور موهومی واقع شود).

2. پایداری نسبی: برای جلوگیری از فراجهش زیاد و رفتار نوسانی، مقدار ضریب میرایی $$\zeta$$ باید رضایت‌بخش باشد. از آن‌جایی که $$\zeta=\cos \Phi$$، زاویه $$\Phi$$‌ نباید نزدیک $$90^\circ$$ باشد.

3. ثابت زمانی: با افزایش اندازه بخش حقیقی (منفی) قطب، ثابت زمانی کم می‌شود (سرعت میل به صفر افزایش می‌یابد).

4. سرعت پاسخ: سرعت پاسخ، با افزایش فاصله $$\omega _n$$ قطب‌ها از مبدا، افزایش می‌یابد.

5. فرکانس طبیعی نامیرا: این فرکانس، برابر با فاصله قطب‌ها از مبدا است. افزایش $$\omega _n$$ قطب‌ها (با $$\zeta $$ ثابت)، سرعت پاسخ را زیاد می‌کند، در حالی که درصد فراجهش تغییری نمی‌کند.

6. فرکانس نوسانات گذرا ($$\omega _n \sqrt{1-\zeta ^2}$$): این فرکانس، فرکانس تشدید یا رزونانس و فرکانس طبیعی میرا نیز نامیده می‌شود که برابر با قسمت موهومی قطب مختلط است.

^^