تحلیل مولفه اساسی (PCA) در پایتون — راهنمای کاربردی
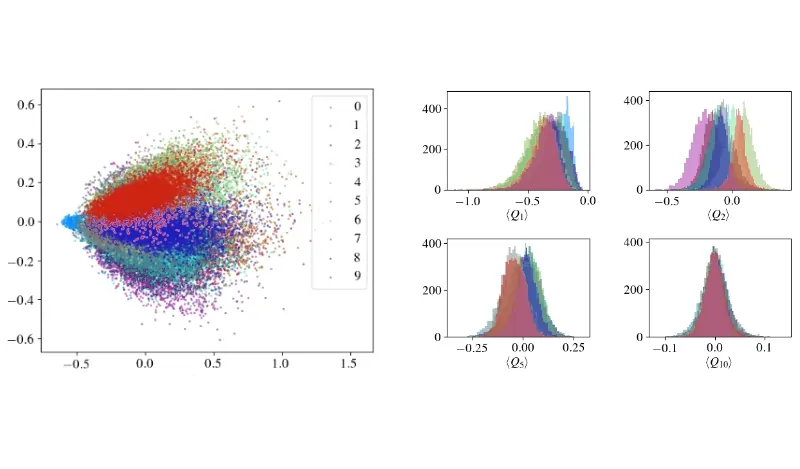
تحلیل مولفه اساسی (PCA) یا (Principal Component Analysis) یک «روش تبدیل خطی» (Linear Transformation Technique) ساده و در عین حال محبوب و کارآمد محسوب میشود. از این روش در کاربردهایی مانند پیشبینی بازار بورس، تحلیل دادههای بیان ژن و بسیاری از دیگر موارد استفاده میشود. در این راهنما، میتوان مشاهده کرد که PCA یک روش «جعبه سیاه» (Black Box) نیست و این امکان وجود دارد که آنچه در این الگوریتم انجام میشود را در تنها سه گام اساسی مشاهده کرد.
مقدمهای از تحلیل مولفه اساسی (PCA)
اندازه دادهها در عصر مدرن، نه فقط یک چالش برای سختافزارهای کامپیوتر، بلکه تنگنایی برای کارایی بسیاری از الگوریتمهای «یادگیری ماشین» (Machine Learning) محسوب میشود. هدف اصلی تحلیلهای PCA شناسایی الگوهای موجود در دادهها است؛ تحلیل مولفه اساسی (PCA) قصد دارد همبستگی بین متغیرها را شناسایی کند. اگر یک همبستگی قوی بین متغیرها وجود داشت، تلاشها برای کاهش ابعاد معنادار خواهد بود. به طور کل، آنچه در PCA به وقوع میپیوندد پیدا کردن جهت واریانس بیشینه در دادههای ابعاد بالا و طرحریزی کردن آن در زیرفضایی با ابعاد کمتر به طوری است که بیشترین اطلاعات حفظ شوند.
PCA در مقایسه با LDA
هم «تحلیل تشخیصی خطی» (Linear Discriminant Analysis | LDA) و هم تحلیل مولفه اساسی (PCA) از جمله روشهای تبدیل خطی هستند. PCA جهتهایی که واریانس دادهها را بیشینه میکنند (مولفه اساسی) مییابد، در حالیکه هدف LDA پیدا کردن جهتهایی است که جداسازی (یا تمایز) بین دستههای گوناگون را بیشینه میکند و میتواند در مسائل دستهبندی الگو (PCA از برچسب کلاس صرفنظر میکند) مورد استفاده قرار بگیرد. به بیان دیگر، PCA کل مجموعه داده را در یک (زیر)فضای دیگر طرحریزی میکند و LDA تلاش میکند تا یک ویژگی مناسب را به منظور ایجاد تمایز بین الگوهایی که به دستههای مختلف تعلق دارند تعیین کند.
PCA و کاهش ابعاد
اغلب، هدف مورد انتظار کاهش ابعاد یک مجموعه داده d بُعدی با طرحریزی آن در یک زیرفضای k بُعدی (که در آن k < d است) به منظور افزایش بازدهی محاسباتی به صورتی است که بخش مهم اطلاعات باقی بماند. پرسش مهمی که در این وهله مطرح میشود آن است که «سایز K که دادهها را به خوبی نشان میدهد چند است؟».
در ادامه، بردارهای ویژه (Eigenvectors) (مولفههای اساسی) برای مجموعه داده محاسبه و همه آنها در یک «ماتریس تصویر» (Projection Matrix) گردآوری میشوند. به هر یک از این بردارهای ویژه یک مقدار ویژه تخصیص داده میشود که میتواند به عنوان طول یا بزرگنمایی بردار ویژه متناظر در نظر گرفته شود. اگر برخی از مقدارهای ویژه دارای بزرگنمایی به طور قابل توجهی بزرگتر از دیگر موارد بودهاند، کاهش مجموعه داده با تحلیل مولفه اساسی (PCA) به یک زیرفضای ابعاد کوچکتر با حذف جفت ویژههایی با «اطلاعات کمتر» معقول است.
خلاصهای از رویکرد PCA
- استانداردسازی دادهها
- به دست آوردن بردارهای ویژه و مقدارهای ویژه از «ماتریکس کواریانس» (Covariance matrix) یا «ماتریس همبستگی» (Correlation Matrix)، یا انجام «تجزیه مقدارهای منفرد» (Singular Vector Decomposition)
- مرتبسازی مقدارهای ویژه به ترتیب نزولی و انتخاب k بردار ویژهای که متناظر با K بزرگترین مقدار ویژه هستند. K تعداد ابعاد زیرفضای ویژگی جدید است (k≤d).
- ساخت ماتریکس تصویر W از K بردار ویژه انتخاب شده
- تبدیل مجموعه داده اصلی X به وسیله W، برای به دست آوردن زیرفضای Kبُعدی Y
آمادهسازی مجموعه داده IRIS
در این راهنما، از مجموعه داده معروف IRIS استفاده خواهد شد که در مخزن یادگیری ماشین UCI (+) وجود دارد. مجموعه داده IRIS دارای اندازهگیریهای مربوط به طول و عرض کاسبرگ و گلبرگ سه گونه مختلف از گیاه زنبق، در مجموع برای ۱۵۰ نمونه است. سه دسته موجود در مجموعه داده IRIS عبارتند از:
- (Iris-setosa (n=50
- (Iris-versicolor (n=50
- (Iris-virginica (n=50
و چهار ویژگی این مجموعه داده عبارتند از:
- طول کاسبرگ به سانتیمتر (sepal length)
- عرض کاسبرگ به سانتیمتر (sepal width)
- طول گلبرگ به سانتیمتر (petal length)
- عرض گلبرگ به سانتیمتر (petal width)
بارگذاری مجموعه داده
به منظور بارگذاری مستقیم دادههای IRIS از مخزن UCI، از کتابخانه «پانداس» (Pandas) استفاده خواهد شد. پانداس کتابخانهای عالی است که کار با دادهها را به چالشی فوقالعاده مبدل میکند.
1import pandas as pd
2
3df = pd.read_csv(
4 filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
5 header=None,
6 sep=',')
7
8df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
9df.dropna(how="all", inplace=True) # drops the empty line at file-end
10
11df.tail()
# split data table into data X and class labels y X = df.ix[:,0:4].values y = df.ix[:,4].values
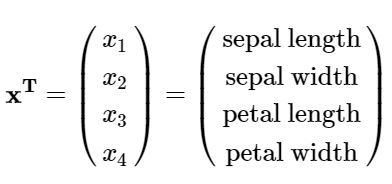
اکنون، مجموعه داده IRIS به صورت یک ماتریس ۱۵۰*۴ ذخیره شده است که ستونهای آن ویژگیهای متفاوت و هر سطریک نمونه گل جدا را مشخص میکند. هر سطر نمونه x را میتوان به صورت یک بردار ۴بُعدی نشان داد.
بصریسازی اکتشافی
در ادامه، برای درک بهتر چگونگی توزیع سه گونه مختلف گل زنبق، نمودارهای هیستوگرام آن رسم خواهند شد.
کدهای مربوطه را در ادامه آوردهایم.
1import plotly.plotly as py
2from plotly.graph_objs import *
3import plotly.tools as tls1# plotting histograms
2
3traces = []
4
5legend = {0:False, 1:False, 2:False, 3:True}
6
7colors = {'Iris-setosa': 'rgb(31, 119, 180)',
8 'Iris-versicolor': 'rgb(255, 127, 14)',
9 'Iris-virginica': 'rgb(44, 160, 44)'}
10
11for col in range(4):
12 for key in colors:
13 traces.append(Histogram(x=X[y==key, col],
14 opacity=0.75,
15 xaxis='x%s' %(col+1),
16 marker=Marker(color=colors[key]),
17 name=key,
18 showlegend=legend[col]))
19
20data = Data(traces)
21
22layout = Layout(barmode='overlay',
23 xaxis=XAxis(domain=[0, 0.25], title='sepal length (cm)'),
24 xaxis2=XAxis(domain=[0.3, 0.5], title='sepal width (cm)'),
25 xaxis3=XAxis(domain=[0.55, 0.75], title='petal length (cm)'),
26 xaxis4=XAxis(domain=[0.8, 1], title='petal width (cm)'),
27 yaxis=YAxis(title='count'),
28 title='Distribution of the different Iris flower features')
29
30fig = Figure(data=data, layout=layout)
31py.iplot(fig)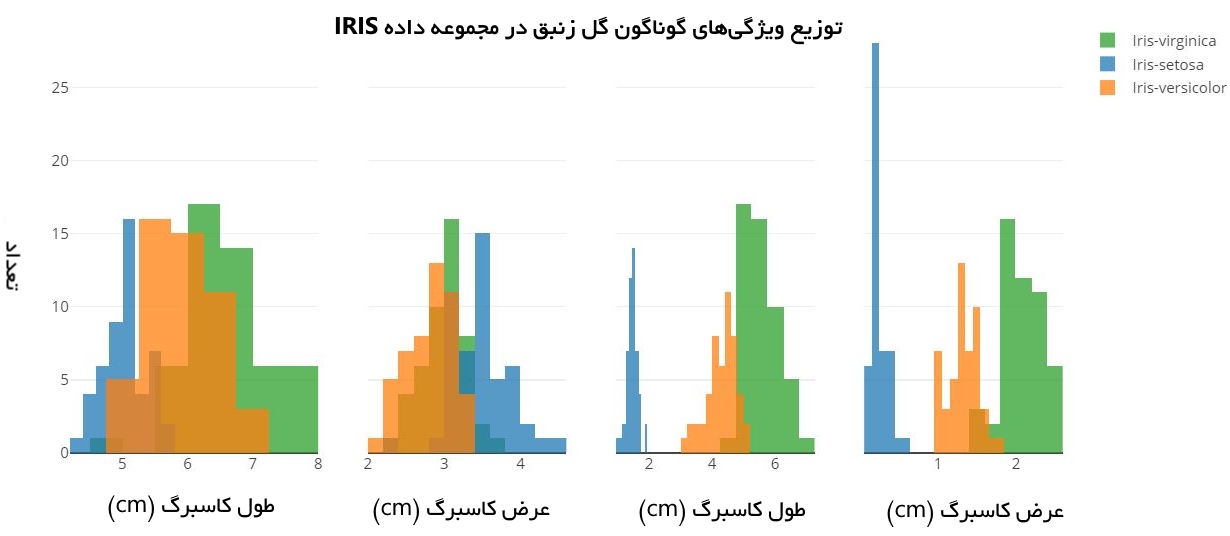
استانداردسازی
استانداردسازی دادهها پیش از تحلیل مولفه اساسی (PCA) روی ماتریس کوارایانس، بستگی به مقیاس اندازهگیری ویژگیهای اصلی دارد.
از آنجا که PCA یک زیرفضای ویژگی دارد که واریانس را در طول محورها بیشینه میکند، برای استانداردسازی دادهها نیز قابل بهرهبرداری است؛ به ویژه اگر در مقیاسهای گوناگون اندازهگیری شده باشد. اگرچه، همه ویژگیها در مجموعه داده IRIS به سانتیمتر اندازهگیری شدهاند، میتوان با تبدیل دادهها به یک مقیاس واحد (میانگین=۰ و واریانس=۱) ادامه داد، که برای کارایی بهینه بسیاری از الگوریتمها یادگیری ماشین لازم است.
1from sklearn.preprocessing import StandardScaler
2X_std = StandardScaler().fit_transform(X)۱. تجزیه ویژه، محاسبه بردارهای ویژه و مقدارهای ویژه
«بردارهای ویژه» (EigenVectors) و «مقدارهای ویژه» (EigenValues) از یک ماتریس کواریانس (همبستگی) نشانگر «هسته» (Core) الگوریتم PCA هستند. بردارهای ویژه (مولفههای اساسی) جهت فضای ویژگی جدید را تعیین میکنند و مقدارهای ویژه بزرگی آنهای را تعیین میکند. به عبارت دیگر، مقدارهای ویژه واریانس دادهها در طول محورهای ویژگی جدید را تعیین میکند.
ماتریکس کواریانس
رویکرد کلاسیک در PCA انجام «تجزیه ویژه» (Eigendecomposition) در ماتریس کواریانس Σ است که یک ماتریس d×d محسوب میشود و هر عنصر در آن نمایانگر کواریانس بین دو ویژگی است. کواریانس بین دو ویژگی به صورت زیر محاسبه میشود:
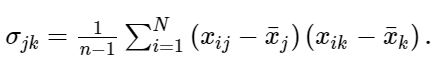
میتوان محاسبه ماتریس کواریانس را با معادله ماتریس زیر انجام داد.
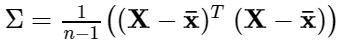
که در آن بردار میانگین
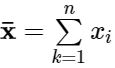
است. بردار میانگین، یک بردار dبُعدی است که در آن هر مقدار نشانگر میانگین نمونه از بردار ویژگی در مجموعه داده است.
1import numpy as np
2mean_vec = np.mean(X_std, axis=0)
3cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
4print('Covariance matrix \n%s' %cov_mat)1Covariance matrix
2[[ 1.00671141 -0.11010327 0.87760486 0.82344326]
3 [-0.11010327 1.00671141 -0.42333835 -0.358937 ]
4 [ 0.87760486 -0.42333835 1.00671141 0.96921855]
5 [ 0.82344326 -0.358937 0.96921855 1.00671141]]راهکار عمیقتر بالا، که به سادگی به منظور اثبات مورد استفاده قرار گرفت را میتوان با تابع cov در کتابخانه NumPy پیادهسازی کرد.
1print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))1NumPy covariance matrix:
2[[ 1.00671141 -0.11010327 0.87760486 0.82344326]
3 [-0.11010327 1.00671141 -0.42333835 -0.358937 ]
4 [ 0.87760486 -0.42333835 1.00671141 0.96921855]
5 [ 0.82344326 -0.358937 0.96921855 1.00671141]]سپس، یک تجزیه ویژه در ماتریس کواریانس انجام میشود.
1cov_mat = np.cov(X_std.T)
2
3eig_vals, eig_vecs = np.linalg.eig(cov_mat)
4
5print('Eigenvectors \n%s' %eig_vecs)
6print('\nEigenvalues \n%s' %eig_vals)1Eigenvectors
2[[ 0.52237162 -0.37231836 -0.72101681 0.26199559]
3 [-0.26335492 -0.92555649 0.24203288 -0.12413481]
4 [ 0.58125401 -0.02109478 0.14089226 -0.80115427]
5 [ 0.56561105 -0.06541577 0.6338014 0.52354627]]
6
7Eigenvalues
8[ 2.93035378 0.92740362 0.14834223 0.02074601]ماتریس همبستگی
در حوزههای «مالی»، ماتریس همبستگی معمولا به جای ماتریس کواریانس استفاده میشود. اگرچه، تجزیه ویژه ماتریس کواریانس (اگر دادههای ورودی استاندارد شده باشند) نتایج مشابهی را مانند تجزیه ویژه روی ماتریس همبستگی به دست میدهد، از این رو ماتریس همبستگی را میتوان به عنوان ماتریس کواریانس نرمال شده درک و محسوب کرد. تجزیه ویژه دادههای استاندارد شده بر پایه ماتریس همبستگی، با بهرهگیری از قطعه کد زیر انجام میشود.
1cor_mat1 = np.corrcoef(X_std.T)
2
3eig_vals, eig_vecs = np.linalg.eig(cor_mat1)
4
5print('Eigenvectors \n%s' %eig_vecs)
6print('\nEigenvalues \n%s' %eig_vals)Eigenvectors [[ 0.52237162 -0.37231836 -0.72101681 0.26199559] [-0.26335492 -0.92555649 0.24203288 -0.12413481] [ 0.58125401 -0.02109478 0.14089226 -0.80115427] [ 0.56561105 -0.06541577 0.6338014 0.52354627]] Eigenvalues [ 2.91081808 0.92122093 0.14735328 0.02060771]
تجزیه ویژه دادههای خام بر مبنای ماتریس همبستگی به صورت زیر است:
1cor_mat2 = np.corrcoef(X.T)
2
3eig_vals, eig_vecs = np.linalg.eig(cor_mat2)
4
5print('Eigenvectors \n%s' %eig_vecs)
6print('\nEigenvalues \n%s' %eig_vals)Eigenvectors [[ 0.52237162 -0.37231836 -0.72101681 0.26199559] [-0.26335492 -0.92555649 0.24203288 -0.12413481] [ 0.58125401 -0.02109478 0.14089226 -0.80115427] [ 0.56561105 -0.06541577 0.6338014 0.52354627]] Eigenvalues [ 2.91081808 0.92122093 0.14735328 0.02060771]
میتوان به وضوح مشاهده کرد که هر سه رویکردی که در بالا تشریح شدند، جفتهای بردار ویژه و مقدار ویژه مشابهی را در خروجی ارائه میکنند. این سه رویکرد، عبارت بودند از:
- تجزیه ویژه ماتریس کواریانس بعد از استانداردسازی دادهها
- تجزیه ویژه ماتریس همبستگی
- تجزیه ویژه ماتریس همبستگی پس از استانداردسازی دادهها
تجزیه مقدارهای منفرد
در حالیکه تجزیه ویژه ماتریس کواریانس یا همبستگی ممکن است بصریتر باشد، اغلب پیادهسازیهای PCA از «تجزیه مقدار منفرد» (Singular Vector Decomposition | SVD) برای بهبود کارایی محاسباتی استفاده میکنند. بنابراین، SVD برای تایید اینکه نتایج در واقع یکسان هستند اجرا میشود.
1u,s,v = np.linalg.svd(X_std.T)
2uarray([[-0.52237162, -0.37231836, 0.72101681, 0.26199559],
[ 0.26335492, -0.92555649, -0.24203288, -0.12413481],
[-0.58125401, -0.02109478, -0.14089226, -0.80115427],
[-0.56561105, -0.06541577, -0.6338014 , 0.52354627]])
۲. انتخاب مولفه اساسی
هدف اصلی الگوریتم تحلیل مولفه اساسی (PCA) کاهش ابعاد فضای ویژگی اصلی با تصویر آن به زیرفضای کوچکتری است که در آن بردارهای ویژه محورها را تشکیل میدهند.
اگرچه، بردارهای ویژه تنها جهت محورهای جدید را تعیین میکنند، زیرا آنها همه دارای طول واحد برابر با یک هستند که میتوان درباره این موضوع با دو خط کد زیر اطمینان حاصل کرد.
1for ev in eig_vecs:
2 np.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev))
3print('Everything ok!')1# Make a list of (eigenvalue, eigenvector) tuples
2eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
3
4# Sort the (eigenvalue, eigenvector) tuples from high to low
5eig_pairs.sort()
6eig_pairs.reverse()
7
8# Visually confirm that the list is correctly sorted by decreasing eigenvalues
9print('Eigenvalues in descending order:')
10for i in eig_pairs:
11 print(i[0])Eigenvalues in descending order: 2.91081808375 0.921220930707 0.147353278305 0.0206077072356
پس از مرتبسازی «جفتهای ویژه» (eigenpairs)، پرسش بعدی این است که «چه تعداد مولفه اساسی برای فضای ویژگی جدید انتخاب خواهد شد؟». یک سنجه مناسب «واریانس توصیف شده» (Explained variation) است که از مقدارهای ویژه قابل محاسبه به شمار میآید. واریانس توصیف شده، بیان میکند که چقدر اطلاعات (واریانس) به هر مولفه اساسی اختصاص دارد.
1tot = sum(eig_vals)
2var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
3cum_var_exp = np.cumsum(var_exp)
4
5trace1 = Bar(
6 x=['PC %s' %i for i in range(1,5)],
7 y=var_exp,
8 showlegend=False)
9
10trace2 = Scatter(
11 x=['PC %s' %i for i in range(1,5)],
12 y=cum_var_exp,
13 name='cumulative explained variance')
14
15data = Data([trace1, trace2])
16
17layout=Layout(
18 yaxis=YAxis(title='Explained variance in percent'),
19 title='Explained variance by different principal components')
20
21fig = Figure(data=data, layout=layout)
22py.iplot(fig)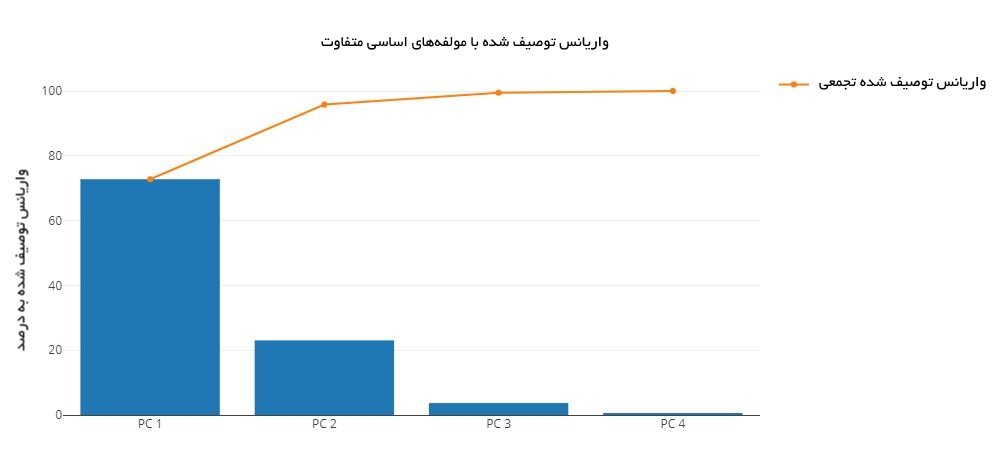
نمودار بالا نشان میدهد که بیشترین واریانس (برای دقیقتر بودن باید گفت ٪۷۲.۷۷ واریانس) به تنهایی به وسیله اولین مولفه اساسی ارائه میشود. دومین مولفه اساسی همچنان دربردارنده اطلاعات است (٪۲۳.۰۳)، در حالی که سومین و چارمین مولفه میتوانند در عین امنیت بدون از دست دادن اطلاعات زیادی حذف شوند. دو مولفه اساسی اول و دوم، در کنار هم در بردارنده ٪۹۵.۸ اطلاعات هستند.
اکنون، نوبت جذابترین بخش کار یعنی ساخت «ماتریس تصویرگر» (Projection Matrix) است که برای تبدیل اطلاعات IRIS به یک زیرفضای ویژگی جدید مورد استفاده قرار میگیرد. اگرچه، نام «ماتریس تصویرگر» ارتباط خوبی با آن دارد، اما اساسا صرفا یک ماتریس از k بردار ویژه به هم ملحق شده است. در اینجا، فضای ویژگی ۴بُعدی، با انتخاب دو بردار ویژه با بالاترین مقدارهای ویژه برای ساخت ماتریس بردار ویژه d×k بُعدی W، به زیرفضای ۲بُعدی کاهش پیدا کرد.
1matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
2 eig_pairs[1][1].reshape(4,1)))
3
4print('Matrix W:\n', matrix_w)('Matrix W:\n', array([[ 0.52237162, -0.37231836],
[-0.26335492, -0.92555649],
[ 0.58125401, -0.02109478],
[ 0.56561105, -0.06541577]]))
۳. تصویر کردن روی فضای ویژگی جدید
در آخرین گام، از ماتریس تصویرگر ۲×۴بُعدی W برای تبدیل نمونهها به یک زیرفضای جدید با معادله Y=X×W استفاده میشود، که در آن Y یک ماتریس ۲×۱۵۰ از نمونههای تبدیل شده است.
1Y = X_std.dot(matrix_w)1traces = []
2
3for name in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
4
5 trace = Scatter(
6 x=Y[y==name,0],
7 y=Y[y==name,1],
8 mode='markers',
9 name=name,
10 marker=Marker(
11 size=12,
12 line=Line(
13 color='rgba(217, 217, 217, 0.14)',
14 width=0.5),
15 opacity=0.8))
16 traces.append(trace)
17
18
19data = Data(traces)
20layout = Layout(showlegend=True,
21 scene=Scene(xaxis=XAxis(title='PC1'),
22 yaxis=YAxis(title='PC2'),))
23
24fig = Figure(data=data, layout=layout)
25py.iplot(fig)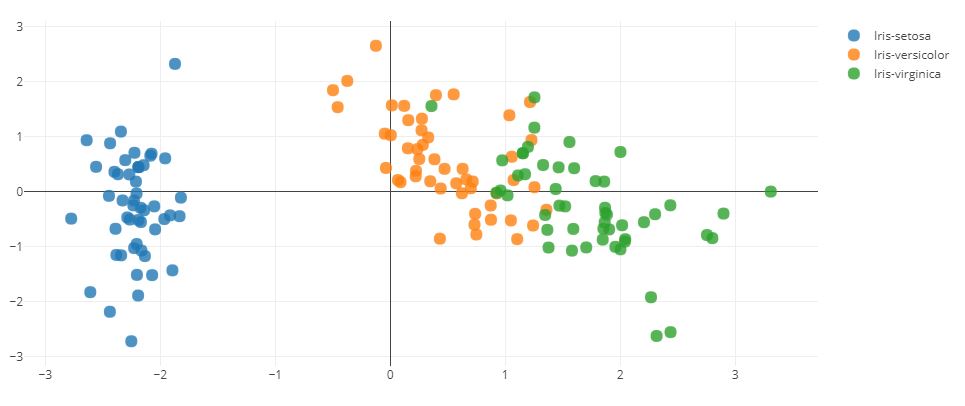
PCA در سایکیتلِرن
برای اهداف آموزشی، کلیه جزئیات لازم برای پیادهسازی تحلیل مولفه اساسی (PCA) و اعمال آن روی مجموعه داده IRIS بیان شد. ولی خوشبختانه، پیادهسازی این الگوریتم در کتابخانه «سایکیتلِرن» (Scikit-learn) موجود است.
1from sklearn.decomposition import PCA as sklearnPCA
2sklearn_pca = sklearnPCA(n_components=2)
3Y_sklearn = sklearn_pca.fit_transform(X_std)1traces = []
2
3for name in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
4
5 trace = Scatter(
6 x=Y_sklearn[y==name,0],
7 y=Y_sklearn[y==name,1],
8 mode='markers',
9 name=name,
10 marker=Marker(
11 size=12,
12 line=Line(
13 color='rgba(217, 217, 217, 0.14)',
14 width=0.5),
15 opacity=0.8))
16 traces.append(trace)
17
18
19data = Data(traces)
20layout = Layout(xaxis=XAxis(title='PC1', showline=False),
21 yaxis=YAxis(title='PC2', showline=False))
22fig = Figure(data=data, layout=layout)
23py.iplot(fig)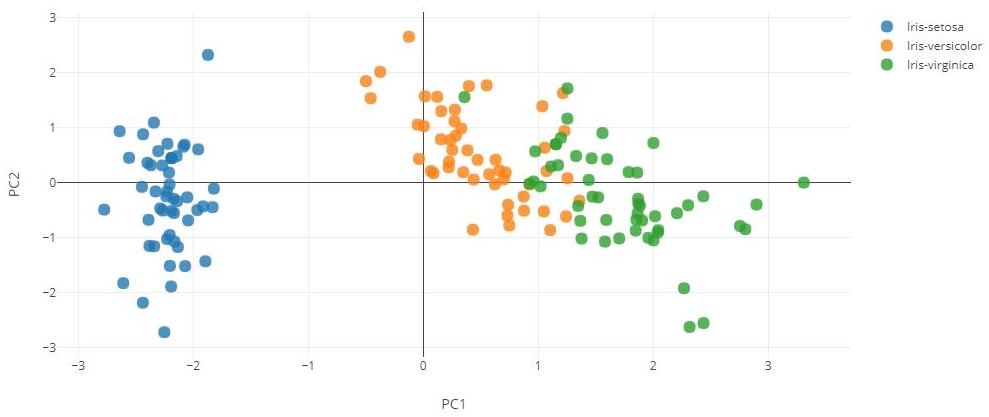
اگر نوشته بالا برای شما مفید بود، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزشهای دادهکاوی یا Data Mining در متلب
- مجموعه آموزشهای مدل سازی، برازش و تخمین
- دادهکاوی (Data Mining) — از صفر تا صد
- یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
^^













با سلام من آموزشهای نرم افزار R را خریداری و مطالعه کردم الان می خواهم PCA به صورت ترسیمهای مختلف که در مقالات خارجی است و CCA آن را در نرم افزار R را در مقالاتم استفاده کنم لطفا اگر آموزشی در این زمینه دارید معرفی کنید با تشکر
با سلام و احترام؛
در رابطه با CCA، مطالعه مطلب تحلیل همبستگی کانونی و تفسیر آن از مجله فرادرس را به شما پیشنهاد میکنیم.
از همراهی شما با مجله فرادرس بسیار خشنود و سپاسگزاریم.
سلام و تشکر بابت مطالب مفیدتون
در صورت امکان برایPCA ,SVM هم فایل ویدیوئی تهیه کنید. قطعا استقبال خواهد شد.
با تشکر
حسین فاتحی
سوال دوم:
الان ما 4 بعد رو تبدیل کردیم به 2 بعد.
یعنی ماتریسی با ابعاد 2*150 .
د واقع کاهش بعد انجام گرفت ولی در عمل ترکیب خطی از کل ویژگیها در ماتریس 2*150 ایجاد شد.
می خواستم بدونم بعد از انجام PCA ، چه کارهایی با داده های با ابعاد جدید میشه انجام داد؟
چون من الان یک ماتریس دیتا با ابعاد 20*100 دارم که اطلاعات خرید پروژه هستند.(100 بسته خرید با 20 مشخصه)
میخواستم بدونم اگر من بخوام براساس بیشترین واریانس داده ، حداکثر بردار ویژه رو نگه دارم(مثلا 90% ) که در نهایت تعداد مولفه های من خواهند بود، چه استفاده ایی از دیتای جدید،مثلا با ابعاد 5*100 می تونم انجام بدم؟
آیا میتونم با این بعد جدید یک معادله رگرسیون براش بسازم؟
آیا میتونم این میزان از دیتا رو به انفیس بدم تا برام یک پترن با قاعده های فازی بسازه که بعد بشه باهاش رفتار Black Box خریدرو در آینده پیش بینی کرد؟
سلام.یک سوال داشتم.
ماتریس نهایی که ساخته میشه با بعد کمتر، (Y = X_std.dot(matrix_w)) در واقع برای ساخت الگو و سایر موارددیگه ازش استفاده خواهد شد به جای ماتریس اولیه(X)؟
یعنی ماتریس نهایی با بعد کمتر بعنوان ماتریس نهایی به جای ماتریس اولیه استفاده می شود؟