آزمایش تصادفی، پیشامد و تابع احتمال

از آنجایی که اصول و مبنای احتمال بر پیشامدهای تصادفی بنا شده است،‌ بهتر است در ابتدا با مفهوم آزمایش تصادفی، پیشامد و تابع احتمال، آشنا شده و سپس وارد فضای احتمال شویم. آزمایش تصادفی با آزمایش‌هایی که در فیزیک یا شیمی انجام می‌شود متفاوت است. در اینگونه آزمایش‌ها معمولا با تکرار آزمایش در شرایط یکسان،‌ نتایج یکسان نیز گرفته می‌شود. ولی در آزمایش تصادفی نتایج با تکرار آزمایش در شرایط یکسان، متفاوت و برمبنای تصادف حاصل می‌شوند.

آزمایش تصادفی

«آزمایش تصادفی» (Random Experiment, Random Trial)، عملی است که دارای خصوصیات زیر باشد:

1. قابلیت تکرار داشته باشد.
2. در شرایط یکسان نتایج متفاوتی داشته باشد.
3. همه نتایج قبل از انجام آزمایش قابل پیش‌بینی باشند.

برای مثال، پرتاب یک سکه که در بیشتر مباحث احتمال به آن اشاره می‌شود، یک آزمایش تصادفی است. زیرا:

1. پرتاب سکه قابل تکرار است.
2. می‌توان نیرو و ارتفاع پرتاب سکه را با استفاده از دستگاه‌های مکانیکی تنظیم کرد (در نتیجه شرایط آزمایش یکسان است).
3. از قبل مشخص است سکه یا از طرف رو (شیر) ظاهر می‌شود یا پشت (خط)

همینطور پرتاب تاس، فاصله محل اصابت تیر از مرکز تخته هدف در ورزش تیر و کمان (با فرض ثابت بودن جهت و میزان وزش باد)، انتخاب یک گزینه از پاسخ‌های چهارگزینه‌‌ای که به زبان چینی نوشته شده باشد (به فرض اینکه از زبان چینی آگاهی نداشته باشیم) و ... از انواع آزمایش‌های تصادفی هستند.

فضای نمونه

مجموعه نتایج ممکن برای یک آزمایش تصادفی را «فضای نمونه» (Sample Space) می‌نامند. معمولا فضای نمونه یک آزمایش تصادفی را با حرف $$\Omega$$ نمایش می‌دهند. برای مثال در پرتاب یک سکه به منظور مشاهده شیر (H) یا خط (T)، فضای نمونه برابر با $$\Omega=\{H,T\}$$ خواهد بود. همچنین اگر دو سکه مستقل از یکدیگر پرتاب شوند (یا یک سکه دوبار پرتاب شود)، فضای نمونه به صورت $$\Omega=\{HH,HT,TH,TT\}$$ درخواهد آمد. منظور از TH مشاهده خط در پرتاب اول و شیر در پرتاب دوم است در حالیکه HT به معنی مشاهده شیر و سپس مشاهده خط در پرتاب دوم است.

همچنین در آزمون زبان چینی که دارای ۱۰ پرسش چهار گزینه‌ای است، اگر تعداد پاسخ‌های صحیح مورد نظر باشد، فضای نمونه برابر است با $$\Omega=\{0,1,2,3,4,5,6,7,8,9,10\}$$.

قابل ذکر است که چنین آزمایش‌هایی دارای فضای نمونه متناهی هستند.

اگر سکه‌ای را تا مشاهده اولین شیر پرتاب کنیم و تعداد پرتاب‌های صورت گرفته تا رسیدن به چنین وضعیتی مورد نظر باشد، فضای نمونه برای این آزمایش تصادفی به صورت  $$\Omega=\{1,2,\ldots\}$$ است، زیرا ممکن است این اتفاق در اولین پرتاب، دومین پرتاب یا ... اتفاق بیافتد. این فضای نمونه را نامتناهی شمارش پذیر می‌نامند.

در ورزش تیر و کمان اگر فاصله محل اصابت تا مرکز تخته ملاک باشد، فضای نمونه برای این آزمایش تصادفی به صورت $$\Omega=[0,r)$$ است، که منظور از r، شعاع تخته هدف در این ورزش است. چنین فضای نمونه‌ای با توجه به اینکه یک فاصله از اعداد حقیقی است، نامتناهی و ناشمارا محسوب می‌شود.

پیشامد

در حالتی که فضای نمونه متناهی باشد، می‌توان گفت هر زیر مجموعه‌ای از فضای نمونه یک پیشامد تلقی می‌شود. در این حالت با توجه به فضای نمونه‌ای مربوط به پرتاب دو سکه، می‌توان $$A=\{TT,TH\}$$ را پیشامد مشاهده خط در اولین پرتاب در نظر گرفت. مشخص است که $$A\subset \Omega$$.

از آنجایی که A یک پیشامد است، انتظار داریم مکمل آن یعنی $$A\prime$$ نیز یک پیشامد باشد. از طرفی خود $$\Omega$$ نیز یک پیشامد خواهد بود زیرا $$\Omega \subset \Omega$$،  پس انتظار داریم که $$\emptyset$$ نیز یک پیشامد باشد. به $$\Omega$$ «پیشامد حتمی» و به $$\emptyset$$ «پیشامد محال» می‌گویند.

در نتیجه اگر F را مجموعه همه زیر مجموعه‌های $$\Omega$$ در نظر بگیریم، به آن «فضای پیشامد» می‌گوییم. مجموعه F باید در شرایط زیر صدق کند:

1. مجموعه تهی ($$\emptyset$$) و فضای نمونه ( $$\Omega$$) باید در F باشند. به این معنی که $$\Omega \in F$$ و $$\emptyset \in F$$.
2. اگر A در F باشد باید مکمل آن یعنی $$A\prime$$ نیز در F باشد.
3. اگر $$A_1, A_2, \ldots$$ دنباله‌ای از پیشامدهای جدا از هم باشند، اجتماع آن‌ها نیز یک پیشامد است، یعنی $$\cup_{i=1}^ \infty A_i \in F$$.

مجموعه‌ای که براساس زیر مجموعه‌های یک فضای نمونه‌ نامتناهی ایجاد شود و در همه شرط‌های اول تا سوم صدق کند، «سیگما-میدان» ($$\sigma-Field$$) یا «سیگما-جبر» ($$\sigma-Algebra$$) گفته می‌شود. پس می‌توان فضای پیشامد را سیگما-میدان حاصل از فضای نمونه در نظر گرفت.

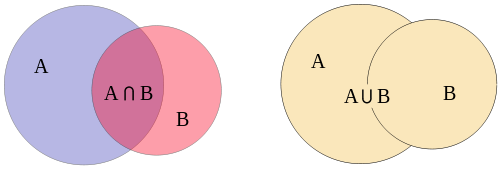
نکته: $$A \cap B$$ را پیشامد رخداد هر دو پیشامد A و B می‌نامند. همچنین پیشامد $$A \cup B$$ نیز به معنی رخداد پیشامد A یا B (یا هر دو) خواهد بود. پیشامد مکمل A یعنی $$A\prime$$ را پیشامد عدم رخداد A در نظر می‌گیرند.

پیشامدهای ناسازگار

اگر A و B دو پیشامد باشند، آن‌ها را ناسازگار گویند، اگر اشتراکشان برابر مجموعه $$\emptyset$$ باشد. یعنی:

$$A\cap B = \emptyset$$

به این ترتیب فقط یا پیشامد A رخ داده یا B و نه هر دو.

دنباله پیشامدهای $$A_1, A_2, \ldots$$ را دو به دو ناسازگار گویند، اگر همزمان فقط یکی از آن‌ها رخ دهد. یعنی:

 $$A_i\cap A_j = \emptyset\;\;\;\;\;\;\;\ ,i,j=1,2,\ldots$$

دنباله پیشامدهای یکنوا

اگر دنباله پیشامدهای $$A_1, A_2, \ldots$$ به صورت صعودی باشند، آن را یکنوا می‌نامیم. یعنی رابطه بین $$A_i$$ ها به صورت زیر باشد.

 $$A_۱\subset A_2 \subset a_3 \subset \ldots$$

البته ممکن است این رابطه به صورت نزولی نیز گفته شود، ولی در هر دو حالت دنباله پیشامدها یکنوا هستند، زیرا می‌توان با ساخت پیشامدهای جدید از روی پیشامدهای نزولی، آن‌ها را به صورت صعودی درآورد.

اصول احتمال و تابع احتمال

با توجه به تعریف فضای نمونه و فضای پیشامد، امکان تعریف تابع احتمال بوجود می‌آید.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

تعریف تابع احتمال: هر تابعی یا نگاشتی از فضای پیشامد به مجموعه اعداد حقیقی اگر در سه اصل زیر صدق کند یک تابع احتمال است.

• اصل اول: مقدار احتمال برای هر پیشامد، نامنفی است. بنابراین اگر A یک پیشامد باشد (یعنی متعلق به فضای پیشامد F باشد)

$$P(A)\geq 0$$

• اصل دوم: مقدار احتمال برای فضای نمونه برابر است با ۱.

$$P(\Omega)=1$$

• اصل سوم: احتمال اجتماع هر دنباله نامتناهی از پیشامدهای دو به دو ناسازگار، برابر با مجموع احتمال پیشامدهای دنباله است.

$$P(\cup_{i=1}^\infty A_i)= \sum_{i=1}^\infty P(A_i)$$

این اصول توسط «آندری کولموگروف» (Andrey Kolmogorov) ریاضی و آماردان روسی در سال 1933، به عنوان اصول تابع احتمال مطرح شد. این کار باعث شد که نظریه احتمال از پشتوانه آنالیز ریاضی و نظریه اندازه برخوردار شود.

براساس این سه اصل قضیه‌های زیادی برای تابع احتمال اثبات شده است. در ادامه به معرفی چند قضیه مهم برای تابع احتمال می‌پردازیم:

۱- مقدار احتمال برای پیشامد $$\emptyset$$ برابر با صفر است.

$$P(\emptyset)=0$$

۲- احتمال اجتماع دو پیشامد ناسازگار برابر با مجموع احتمال آن‌ها است.

$$P(A\cup B)= P(A)+P(B)$$

۳- مقدار احتمال برای مکمل یک پیشامد A برابر با تفاضل مقدار احتمال پیشامد A از ۱ است.

$$P(A\prime)= 1-P(A)$$

۴- اگر پیشامد A زیر مجموعه پیشامد B باشد،‌ مقدار احتمال نیز برای پیشامد A از B کمتر است.

$$A\subset B \rightarrow P(A)\leq P(B)$$

۵- اگر C پیشامدی باشد که از اجتماع دو پیشامد A و B ایجاد شده باشد، احتمال پیشامد C برابر است با مجموع پیشامدهای A و B منهای پیشامد $$A\cap B$$.

$$P(C)=P(A\cup B)=P(A)+P(B)-P(A\cap B)$$

پیوستگی تابع احتمال

برطبق اصل سوم می‌توان به بررسی پیوستگی تابع احتمال پرداخت.

قضیه پیوستگی تابع احتمال: دنباله‌ای نامتناهی و یکنوا از پیشامدهای جدا از هم مثل $$A_n$$‌ها را در نظر بگیرید، آنگاه حد احتمال این پیشامدها برابر با احتمال حد پیشامدها است. یعنی:

$$lim_{n\to \infty} P(A_n)=P(lim_{n\to \infty} A_n)$$

در ادامه به بررسی چند مثال به منظور روشن شدن مفهوم تابع احتمال و شیوه محاسبه آن می‌پردازیم.

مثال‌ ۱

فرض کنید فردی مسیر محل کار تا منزلش را به دو شیوه می‌تواند طی کند. فضای نمونه و فضای پیشامد برای او به چه صورت است؟

اگر شیوه اول را با A و شیوه دوم را با B نشان دهیم، فضای نمونه به صورت $$\Omega = \{A,B\}$$ نوشته خواهد شد. همچنین فضای پیشامد نیز برابر است با $$F=\{A,B,\emptyset,\Omega \}$$، زیرا واضح است که $$A\cup B = \Omega$$  و $$A \cap B = \emptyset$$. همینطور مشخص است که $$A\prime = B$$ و $$B\prime = A$$.

احتمال اینکه روش اول را انتخاب کند برابر با 0.4 است. احتمال اینکه روش دوم را برای رفتن به منزل انتخاب کند چقدر است؟

$$P(B)=P(A\prime)=1-P(A)=1-0.4=0.6$$

احتمال اینکه او از این دو روش استفاده نکند چقدر خواهد بود؟ طبق قضیه شماره ۵ می‌توان نوشت: $$P(A\cap B)= P(A\cap B)-P(A)-P(B)$$. حال با به کار بردن این تساوی برای پیشامدهای مکمل داریم:

$$P(A\prime \cap B\prime)= P(A\prime \cup B\prime )-P(A\prime )-P(B\prime )= p(\Omega)-(1-0.4)-(1-0.6)=1-0.6-0.4=0$$

مثال ۲

فرض کنید A، B و C سه پیشامد باشند و فضای نمونه از این سه پیشامد تشکیل شده. حال به دنبال پاسخ برای پرسش‌های زیر هستیم.

• پیشامد اینکه هر سه با هم اتفاق بیافتند، چیست؟

با توجه به نکته‌ای که در قسمت پیشامد گفته شد، $$A \cap B\cap C$$ پیشامد مورد نظر است.

• احتمال اینکه هیچکدام اتفاق نیافتند کدام است؟

با توجه به اینکه سه پیشامد، فضای نمونه را می‌سازد، $$\Omega =A \cup B \cup C$$ که به معنی رخداد حداقل یکی از پیشامد‌ها است.  در نتیجه احتمال رخداد هیچکدام از پیشامدها برابر است با

$$P(A\prime \cap B\prime \cap C \prime)=P(\Omega')=1-P(\Omega)=1-1=0$$

• احتمال اینکه فقط دو پیشامد رخ دهد چگونه محاسبه می‌شود؟

$$P(A\cap B\cap C')+P(A\cap C\cap B')+P(B\cap C\cap A')$$

مثال ۳

دو پیشامد A و B‌ در فضای پیشامد F هستند و $$P(A)=a$$ و $$P(B)=b$$. حداکثر مقدار برای $$P(A\cup B)$$ چقدر خواهد بود؟

طبقه قضیه ۵ می‌دانیم $$P(C)=P(A\cup B)=P(A)+P(B)-P(A\cap B)$$ ولی از مقدار $$P(A\cap B)$$  اطلاعی نداریم. مشخص است که مقدار احتمال نامنفی است یعنی برای هر پیشامد مانند $$A$$ و $$B$$ داریم $$P(A)\geq 0$$ و $$P(B)\geq 0$$.

از طرفی چون $$A\cap B\subset A$$ و $$A\cap B\subset B$$، نتیجه می‌گیریم که:

$$P(A\cap B) \leq P(A) \;\;, P(A\cap B) \leq P(B) \rightarrow P(A\cap B)\leq \min(P(A),P(B))=\min(a,b)$$

پس می‌توانیم برای پیدا کردن حداقل مقدار احتمال اجتماع این دو پیشامد، بنویسیم:

$$P(A\cup B)\geq P(A)+P(B)-\min(a,b)=a+b-\min(a,b)$$

از طرفی می‌دانیم هر پیشامد زیر مجموعه اجتماع آن با هر پیشامد دیگری است. به این ترتیب مشخص است که رابطه‌های $$A \subset A\cup B$$ و $$B \subset A \cup B$$ برقرار است. در نتیجه خواهیم داشت:

$$P(A) \leq P(A\cup B) , P(B) \leq P(A\cup B) \rightarrow P(A \cup B ) \geq \max( P(A),P(B))$$

نکته: فرض کنید $$\min(a,b) = a$$ باشد، پس مشخص است که $$\max(a,b)=b$$ و برعکس، اگر $$\min(a,b)=b$$ باشد، آنگاه $$\max)a,b)=a$$ خواهد بود. در نتیجه رابطه بالا و رابطه قبلی یکی هستند.

برای مشخص کردن حداکثر مقدار $$P(A\cup B)$$ کافی است که $$A\cap B=\emptyset$$ باشد. آنگاه

$$P(A\cup B)\leq P(A)+P(B)-0=a+b$$

به این ترتیب اگر $$P(A)=0.3$$ و $$P(B)=0.5$$ باشد، آنگاه حداقل مقدار برای $$P(A\cup B)$$ برابر خواهد بود با $$P(A\cup B)\geq 0.5+0.3-\min(0.5,0.3)=0.5$$ که می‌تواند همان $$\max \Big(P(A), P(B) \Big)= 0.5$$ باشد.

همچنین حداکثر مقدار برای $$P(A\cup B)$$‌ نیز برابر با 0.5+0.3=0.8 خواهد بود. زیرا می‌توان نوشت:

 $$0.5+0.3-0.3=0.5\leq P(A\cup B)\leq P(A)+P(B)=0.5+0.3=0.8$$

مثال ۴

در ورزش تیر و کمان، یک فرد مبتدی در جلسه اول خود به صفحه‌ای دایره‌ای شکل به شعاع ۳۰ سانتی‌متر تیراندازی می‌کند. اگر او طوری تیراندازی کند که محل برخورد تیر با هدف به صورت تصادفی باشد، احتمال اینکه تیر او به فاصله حداکثر ۵ سانتی‌متری از مرکز صفحه هدف (سیبل) برخورد کند چقدر است؟

این احتمال را می‌توان برحسب مساحتی که تیر از مرکز صفحه هدف دارد نسبت به مساحت دایره سیبل محاسبه کرد. در نتیجه نسبت این دو مساحت را احتمال در نظر می‌گیریم. اگر پیشامد A‌ را مساحت دایره‌ای با شعاع ۵ سانتی‌متری از مرکز سیبل در نظر بگیریم، فضای نمونه نیز مساحت کل دایره سیبل خواهد بود. نسبت این دو مساحت احتمال را نشان می‌دهد.

$$P(A)=\dfrac{3.14\times 5^2}{3.14\times 30^2}=\dfrac{78.5}{2826}=0.03$$

همچنین برای محاسبه اصابت تیر خارج از دایره‌ای به مرکز ۵ سانتی‌متر نیز از پیشامد مکمل A استفاده می‌کنیم:

$$P(A')=1-P(A)=1-0.03=0.97$$