متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

متغیر تصادفی «دو جمله‌ای» (Binomial) مرتبط با آزمایش تصادفی برنولی است. اگر یک آزمایش برنولی با پارامتر ثابت p را n بار بطور مستقل تکرار کنید، جمع متغیرهای تصادفی برنولی ایجاد شده، یک متغیر تصادفی با توزیع دو جمله‌ای را می‌سازد.

از آنجایی که ضرایب بسط دو جمله‌ای $$(a+b)^n$$ که به ضرایب خیام-پاسکال نیز مشهور است، با تابع احتمال این متغیر تصادفی مرتبط است، نام این نوع متغیر تصادفی، دو جمله‌ای انتخاب شده.

از متغیر تصادفی و توزیع دو جمله‌ای برای مدل‌سازی تعداد موفقیت‌ها در nبار نمونه‌گیری با جایگذاری از جمعیت با حجم N بهره گرفته می‌شود. در این حالت احتمال موفقیت می‌تواند به صورت $$\frac{N_A}{N}$$ برآورد شود (در اینجا $$N_A$$ تعداد اعضای از جامعه است که ویژگی A را دارند.) از آنجایی که باید پارامتر توزیع برنولی (احتمال موفقیت) ثابت باشد از نمونه‌گیری با جایگذاری استفاد شده است. زیرا اگر نمونه‌گیری بدون جایگذاری باشد، احتمال موفقیت در هر نوبت از نمونه‌گیری متفاوت خواهد بود و تعداد موفقیت‌ها دارای توزیع «فوق‌هندسی» (Hyper-geometric) خواهند شد.

از آنجایی که متغیر تصادفی و توزیع دو جمله‌ای براساس متغیر تصادفی برنولی ساخته می‌شوند بهتر است ابتدا مطلب متغیر تصادفی و توزیع برنولی --- به زبان ساده را مطالعه کنید.

متغیر تصادفی دو جمله‌ای

مجموع n متغیر تصادفی برنولی مستقل با پارامتر یکسان، دارای توزیع دو جمله‌ای است و اگر $$X$$ چنین متغیر تصادفی باشد می‌نویسیم $$X\sim B(n,p)$$ و می‌خوانیم X‌ دارای توزیع دو جمله‌ای با پارامترهای n و p است.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

برای مثال اگر یک سکه نااریب را ۱۰ بار پرتاب کنیم، تعداد شیرهای مشاهده شده دارای توزیع دو جمله‌ای با پارامترهای ۱۰ و ۱/۲ است.

نکته: منظور از سکه نااریب، سکه‌ای است که احتمال شیر یا خط آمدن برای آن برابر باشد یعنی $$p=(1-p)=q=\tfrac{1}{2}$$.

تابع احتمال برای متغیر تصادفی دو جمله‌ای

با توجه به اینکه متغیر تصادفی دو جمله‌ای از حاصل جمع n متغیر تصادفی برنولی ساخته می‌شود،‌ مقدارهای نامنفی و گسسته را اختیار می‌کند. پس «تکیه‌گاه» (Support) یا مجموعه مقدارهای متغیر تصادفی به صورت $$\{0,1,2,\ldots,n\}$$ خواهد بود. فرم تابع احتمال یا تابع جرم احتمال برای متغیر تصادفی دو جمله‌ای با پارامترهای n و p به صورت زیر است:

$$\displaystyle P(X=x) = (^n_x) p^x(1-p)^{(n-x)}=(^n_x)p^xq^{(n-x)}\;\;\;\ ,x=0,1,2,\ldots,n$$

که منظور از $$(^n_x)$$ ترکیب x از n است که به فرم زیر محاسبه می‌شود:

$$(^n_x)=\dfrac{n!}{x!(n-x)!}$$

برای آشنایی با مفهوم فاکتوریل و بسط دو جمله‌ای به آموزش قضیه بسط دو جمله ای و مثلث خیام مراجعه کنید.

در تابع احتمال بالا مشخص است که تعداد x موفقیت با احتمال p برای هر کدام و تعداد n-x‌ شکست با احتمال رخداد $$1-p$$ وجود دارد. به نظر می‌رسد تنها ترکیب قرارگیری این موفقیت‌ها و شکست‌ها که همان ضرایب دو جمله‌ای است، برای کامل کردن تابع احتمال لازم است.

نکته: مشخص است که توزیع برنولی حالت خاصی از توزیع دو جمله‌ای با پارامترهای ۱ و p است. در این حالت اگر X‌ متغیر تصادفی برنولی باشد، می‌نویسیم: $$X\sim B(1,p)$$‌

مثال 1

احتمال آنکه در ۱۰ بار پرتاب سکه نااریب ۶ بار شیر مشاهده شود برابر خواهد بود با:

$$P(X=6) = {10 \choose 6}(0.5)^{(6)}\times (0.5)^{10-6}=210\times (\tfrac{1}{2})^{10}=0.205$$

اگر این کار را برای تکیه‌گاه $$X$$ با مجموعه مقدارهای (x=0,1,2,3,4,5,6,7,8,9,10) انجام دهیم، می‌توانیم نمودار توزیع احتمال را برای این مثال ترسیم کنیم.

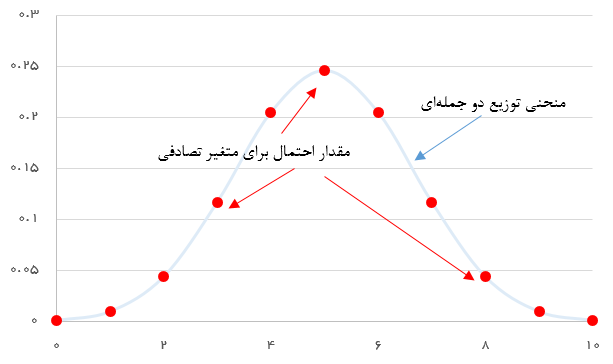
همانطور که در نمودار دیده می‌شود، اگر نقطه‌های احتمال را به یکدیگر متصل کنیم، شکلی شبیه توزیع نرمال بدست خواهد آمد که نشان می‌دهد با افزایش تعداد آزمایش‌ها، توزیع دو جمله‌ای به توزیع نرمال نزدیک می‌شود.

تابع توزیع احتمال دو جمله‌ای

تابع توزیع احتمال متغیر تصادفی X در نقطه x که با $$F_{\large X}(x)$$ نشان داده می‌شود به صورت زیر تعریف می شود:

$$F_{\large X}(x)=P(X\leq x)=\sum_{k=0}^x P(X=k)$$

توجه داشته باشید که منظور از $$F_{\large X}(x)$$، تابع توزیع احتمال برای متغیر تصادفی $$X$$‌ (با حرف بزرگ انگلیسی) در نقطه $$\small x$$ (با حرف کوچک انگلیسی) است که نشان می‌دهد باید تابع توزیع احتمال به ازاء آن محاسبه شود.
البته برای محاسبه تابع توزیع احتمال متغیر تصادفی دو جمله‌ای، جدول‌هایی نیز بر حسب n و p وجود دارد که برای xهای مختلف تنظیم شده. یکی از این گونه جدول‌ها در تصویر زیر دیده می‌شود. باید توجه داشت که مقدارهای درون جدول توزیع احتمال دو جمله‌ای، مقدار احتمال را تا نقطه x نشان می‌دهند و نه در نقطه‌ x.

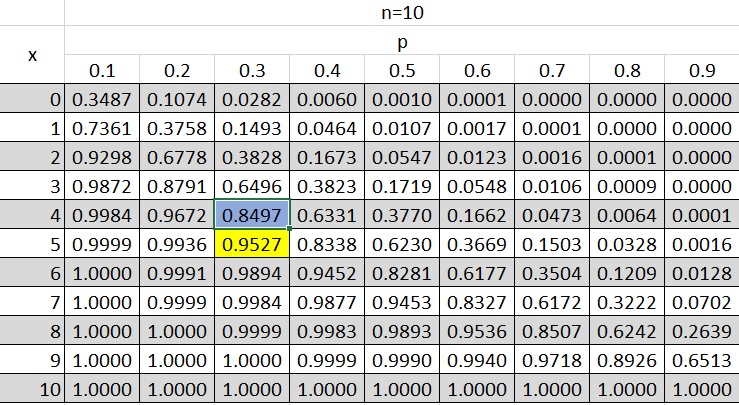
مثال ۲

در ۱۰ بار پرتاب یک سکه اریب که شانس مشاهده شیر برای آن برابر با 0.3 است، احتمال مشاهده ۵ شیر طبق جدول به صورت زیر محاسبه می‌شود.

$$P(X=x)=P(X\leq x)-P(X\leq x-1)=0.9527-0.8497=0.1029$$

البته اگر براساس تابع احتمال محاسبات را طبق مراحل زیر انجام بدهیم به همین مقدار خواهیم رسید.

$$P(X=5) = (^{10}_5)(0.3)^{(5)}\times (0.7)^{(10-5)}=252\times (0.004)=0.1029$$

میانگین و واریانس متغیر تصادفی دو جمله‌ای

با توجه به رابطه‌ای که متغیر تصادفی برنولی با دو جمله‌ای دارد می‌توان امید-ریاضی و واریانس متغیر تصادفی دو جمله‌ای را برحسب متغیر تصادفی برنولی محاسبه کرد. این محاسبات در ادامه آورده شده است.

اگر X یک متغیر تصادفی دو جمله‌ای با پارامترهای n و p‌ باشد، می‌توان آن را برحسب مجموع n متغیر تصادفی برنولی مستقل مثل $$Y_i$$ با پارامتر p نوشت، یعنی $$X=\sum Y_i$$. بنابراین برای محاسبه امید-ریاضی خواهیم داشت:

$$E(X)=E(\sum_{i=1}^n Y_i)=\sum(EY_i)=\sum_{i=1}^n p=np$$

برای محاسبه واریانس متغیر تصادفی دو جمله‌ای نیز از همین روش استفاده می‌کنیم.

$$Var(X)=Var(\sum_{i=1}^nY_i)=\sum_{i=1}^n Var(Y_i)=\sum_{i=1}^n pq=npq$$

زیرا $$Y_i$$ها مستقل هستند، پس می‌توان واریانس مجموع را به صورت جمع واریانس‌ها نوشت.

مثال 3

یک تاس نااریب (که شانس مشاهده هر عدد برابر با 1/6 است) را ۱۰ بار مستقلا پرتاب می‌کنیم. پس اگر X را تعداد مشاهده شش در نظر بگیریم با یک آزمایش دو جمله‌ای سروکار داریم و می‌توانیم توزیع متغیر تصادفی X را به صورت  $$X\sim B(10,\frac{1}{6})$$ در نظر بگیریم.

در نتیجه امید-ریاضی یعنی متوسط تعداد شش‌های مشاهده شده در ۱۰ بار پرتاب این تاس، برابر با $$10\times \tfrac{1}{6}=1.67$$‌ خواهد بود، یعنی حدود ۲ بار عدد شش در ۱۰ بار پرتاب تاس، مشاهده می‌شود. همینطور، واریانس برای تعداد شیرهای مشاهده شده برابر با $$10\times \tfrac{1}{6}\times \tfrac{5}{6}=1.39$$ محاسبه می‌شود.

جمع دو متغیر تصادفی دو جمله‌ای

اگر $$X\sim B(n,p)$$ و $$Y\sim B(m,p)$$ مستقل از یکدیگر باشند، آنگاه $$Z=X+Y\sim B(n+m,p)$$ دارای فرم تابع احتمال به صورت زیر خواهد بود:

$$P(Z=z) = (^{n+m}_{\;\;z})p^z(1-p)^{(n+m-z)}= (^{n+m}_{\;\;z})p^zq^{(n+m-z)}\;\;\;\ ,x=0,1,2,\ldots,n+m$$

تقریب احتمال دو جمله‌ای برحسب تابع توزیع نرمال

با توجه به تصویر ۱ و توضیحات مربوط به مثال ۱، به منظور جلوگیری از محاسبات سنگین برای فاکتوریل، از تقریب نرمال برای محاسبه احتمال متغیر تصادفی دو جمله‌ای می‌توان استفاده کرد. برای چنین کاری کافی است که میانگین و واریانس توزیع دو جمله‌ای مشخص باشد.

فیلم آموزش کنترل کیفیت آماری – جامع و با نکات کاربردی در فرادرس

کلیک کنید

برای متغیر تصادفی $$X\sim B(n,p)$$، اگر n (تعداد نمونه) به حد کافی بزرگ و p کوچک باشد، بطوری که np عدد مناسبی باشد، می‌توان گفت که X دارای توزیع نرمال با میانگین np و واریانس npq است. یعنی بنویسیم $$X\sim N(np,npq)$$ حال با استفاده از جدول‌های تابع توزیع احتمال نرمال می‌توان مقدار تابع توزیع احتمال برای متغیر تصادفی X را پیدا کرد.

برای پیدا کردن تقریب میزان احتمال دو جمله‌ای در نقطه x به صورت زیر عمل می‌کنیم.

$$P(X=x)=p(X\leq x)-P(x\leq x-1)$$

بر طبق مثال 3 با توجه به $$np=1.67$$ که عددی مناسبی است (زیرا p کوچک و n‌ تقریبا بزرگ است) مقدار احتمال با استفاده از تقریب نرمال برای x=6 به شکل زیر محاسبه می‌شود:

$$P(X=6)=P(X\leq 6)-P(x\leq 5)=0.9998-0.9974=0.0024$$

مقدار 0.9998 و 0.9974 از طریق جداول توزیع نرمال استاندارد بدست آمده‌اند. برای آشنایی با نحوه محاسبه این مقدارها می‌توانید به مطلب آموزشی جدول توزیع نرمال استاندارد – به زبان ساده مراجعه کنید.

حال اگر براساس تابع احتمال توزیع دو جمله‌ای، محاسبات را انجام دهیم، خواهیم داشت:

$$P(X=6)=(^n_x)p^xq^{(n-x)}=(^{10}_6)(\tfrac{1}{6})^6(\tfrac{5}{6})^4=0.0022$$

که با مقدار تقریب نرمال بسیار نزدیک است.