همه چیز درباره‌ی هذلولی — به زبان ساده

معمولاً فضاپیماها در یک مسیر هذلولی شکل حرکت می‌کنند. این فضاپیماها از تکنیکی موسوم به «تیرکمان گرانشی» (gravitational slingshot) و از نیروی جاذبه‌ی یک سیاره برای تغییر مسیر حرکت خود و شتاب گرفتن استفاده می کنند. هنگامی که چنین اتفاقی رخ می‌دهد، مسیر حرکت فضاپیما هذلولی شکل خواهد بود.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

منحنی که فاصله‌ی هر نقطه‌ی آن از یک نقطه‌ی ثابت (کانون هذلولی) به فاصله‌ی همان نقطه از یک خط راست ثابت (خط راهنما) نسبت ثابتی می‌باشد.

این نسبت ثابت «خروج از مرکز» نامیده می‌شود و برای یک هذلولی همیشه بزرگتر از 1 است. ضمناً هذلولی یک منحنی باز می‌باشد و انتهایی ندارد. تا بدین جای کار با یک منحنی آشنا شده‌ایم، اما در حقیقت هذلولی از دو منحنی جدا از هم که تصویر یکدیگرند تشکیل شده‌است. به شکل زیر توجه‌کنید:

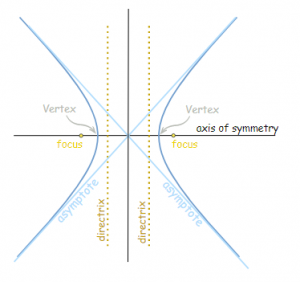
در این شکل می‌بینیم:

• در هر طرف یک خط راهنما و یک کانون وجود دارد.
• محور تقارن (axis of symmetry) که از کانون‌ها گذشته و بر خطوط راهنما عمود است.
• دو رأس دارد (نقاطی که منحنی تیزترین تغییر جهت را دارد).

مجانب‌ها (asymptotes) بخشی از هذلولی نیستند، اما نشان می‌دهند اگر منحنی در چهار جهت تا بی‌نهایت ادامه پیدا کند، چگونه خواهد بود. ضمناً، خط تقارن دیگری نیز وجود دارد که منحنی‌های جدا از هم هذلولی نسبت به آن تصویر شده‌اند.

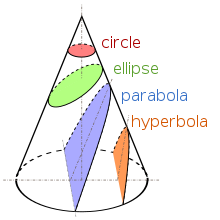
بخش مخروطی

با برش‌دادن یک مخروط می‌توان به یک هذلولی رسید. برش لازم برای رسیدن به یک هذلولی، تیزتر از حالتی است که می‌خواهیم به یک سهمی دست پیدا کنیم؛ اما لازم نیست که این برش با محور مخروط موازی باشد. لذا هذلولی بخشی از یک مخروط است.

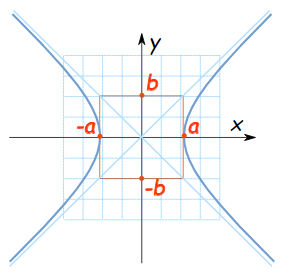
معادله‌ی هذلولی

با قرار دادن هذلولی در صفحه‌ی x-y، به‌گونه‌ای که مرکز آن در مبدأ مختصات قرار بگیرد، معادلات منحنی ها به شکل زیر خواهد بود:

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

همچنین:

1. یک رأس در (a, 0) و رأس دیگر در (a, 0-) قرار دارد.
2. معادله‌ی هذلولی شباهت زیادی به معادله‌ی بیضی (x²/a² + y²/b² = 1) دارد، به غیر از اینکه به جای «+» آن «-» قرار دارد.
3. معادله‌ی خطوط مجانب به صورت زیر است:

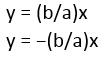
خروج از مرکز

خروج از مرکز (که معمولاً با حرف e نشان داده می‌شود) میزان انحراف هذلولی از یک دایره‌ی کامل بودن را نشان می‌دهد.

در این شکل داریم:

• P نقطه‌ای دلخواه روی منحنی است.
• F کانون هذلولی است.
• N نقطه‌ای روی خط راهنما است، لذا خط PN بر خط راهنما عمود است.

نسبت $$\frac{PF}{PN}$$ خروج از مرکز هذلولی نامیده می‌شود. این مقدار برای یک هذلولی همیشه بزرگتر از 1 می‌باشد. خروج از مرکز را می‌توان از رابطه‌ی زیر نیز به دست آورد:

در این فرمول از a و b نشان داده شده در شکل‌های قبل استفاده می‌شود.

لاتوس رکتام

«لاتوس رکتام» (Latus Rectum) برگرفته از لغت لاتین Latus به معنای «جهت» و لغت Rectum به معنای «سرراست» می‌باشد. لاتوس رکتام خطی است که از کانون‌ها گذشته و با خط راهنما موازی می‌باشد. طول این پاره خط از رابطه‌ی 2b²/a به دست می‌آید.

فیلم آموزش ریاضیات گسسته – پایه دوازدهم در فرادرس

کلیک کنید

اگر تمایل به مطالعه بیشتر در مورد این موضوعات را داشته باشید؛ شاید آموزش های زیر نیز برای شما مفید باشند:

• سطح مقطع در هندسه — به زبان ساده
• تعریف حلقه و محاسبات آن در هندسه — به زبان ساده
• حرکت انتقالی در ریاضیات — به زبان ساده
• تقارن چرخشی در اشکال دوبعدی — به زبان ساده

#

منبع