داده کاوی . هوش مصنوعی

درخت تصمیم و جنگل تصادفی در R — راهنمای کاربردی

آخرین به‌روزرسانی: ۲۵ اردیبهشت ۱۳۹۸
زمان مطالعه: ۴ دقیقه

«درخت تصمیم» (Decision tree) یک راهکار بسیار قدرتمند بصری برای تحلیل یک سری از خروجی‌های پیش‌بینی شده برای یک مدل مشخص است. همچنین، از این الگوریتم اغلب به عنوان مکمل (و یا حتی جایگزین) تحلیل «رگرسیون» (Regression) در تعیین اینکه چگونه یک سری از «متغیرهای توصیفی» (Explanatory Variables) یک متغیر وابسته را تحت تاثیر قرار می‌دهند استفاده می‌شود. در مثال بیان شده در این مطلب، تاثیر متغیرهای توصیفی «سن» (age)، «جنسیت» (gender)، «مایل» (miles)، «اعتبار» (debt) (منظور اعتبار کارت بانکی یا همان کارت اعتباری فرد است) و «درآمد» (income) بر «متغیر وابسته» (dependent variable) «قیمت خودرو» (car sales) با استفاده از درخت تصمیم و «جنگل تصادفی» (Random Forest) تحلیل خواهد شد. مجموعه داده مورد استفاده در این مطلب، از مسیر (+) قابل دانلود است.

فهرست مطالب این نوشته
مساله دسته‌بندی و درخت تصمیم
هرس کردن درخت
حل مساله رگرسیون با درخت تصمیم
جنگل تصادفی

مساله دسته‌بندی و درخت تصمیم

ابتدا، مجموعه داده بارگذاری و متغیر پاسخ ساخته می‌شود (که برای درخت تصمیم مورد استفاده قرار می‌گیرد زیرا نیاز به تبدیل فروش از متغیر عددی به طبقه‌ای وجود دارد):

#Set Directory and define response variable
setwd("C:/Users/michaeljgrogan/Documents/a_documents/computing/data science/datasets")
fullData <- read.csv("cars.csv")
attach(fullData)

fullData$response[CarSales > 24000] <- ">24000"
fullData$response[CarSales > 1000 & CarSales <= 24000] <- ">1000 & <24000"
fullData$response[CarSales <= 1000] <- "<1000"
fullData$response<-as.factor(fullData$response)
str(fullData)

سپس، داده‌های آموزش و آزمون ساخته می‌شود (داده‌هایی که برای ساخت مدل مورد استفاده قرار خواهد گرفت و سپس داده‌هایی که برای آزمودن مدل استفاده می‌شوند).

#Create training and test data
inputData <- fullData[1:770, ] # training data
testData <- fullData[771:963, ] # test data

سپس، درخت دسته‌بندی ساخته می‌شود.

#Classification Tree
library(rpart)
formula=response~Age+Gender+Miles+Debt+Income
dtree=rpart(formula,data=inputData,method="class",control=rpart.control(minsplit=30,cp=0.001))
plot(dtree)
text(dtree)
summary(dtree)
printcp(dtree)
plotcp(dtree)
printcp(dtree)

توجه به این نکته لازم است که cp value چیزی است که سایز درخت مطلوب را تعیین می‌کند (در ادامه مشاهده می‌شود که خطای نسبی X-val هنگامی که سایز درخت برابر با ۴ است کمینه می‌شود). بنابراین، درخت تصمیم با استفاده از متغیر dtree و در نظر گرفتن این متغیر ساخته می‌شود.

> summary(dtree)

Call:
rpart(formula = formula, data = inputData, method = "class", 
    control = rpart.control(minsplit = 30, cp = 0.001))
  n= 770 

           CP nsplit
1 0.496598639      0
2 0.013605442      1
3 0.008503401      6
4 0.001000000     10
  rel error    xerror
1 1.0000000 1.0000000
2 0.5034014 0.5170068
3 0.4353741 0.5646259
4 0.4013605 0.5442177
        xstd
1 0.07418908
2 0.05630200
3 0.05854027
4 0.05759793

هرس کردن درخت

سپس، درخت تصمیم «هرس» (pruned) می‌شود و طی آن «گره‌های» (nodes) نامناسب از درخت برای جلوگیری از «بیش‌برازش» (Overfitting) داده‌ها حذف می‌شوند.

> #Prune the Tree and Plot
pdtree<- prune(dtree, cp=dtree$cptable[which.min(dtree$cptable[,"xerror"]),"CP"])
plot(pdtree, uniform=TRUE,
     main="Pruned Classification Tree For Sales")
text(pdtree, use.n=TRUE, all=TRUE, cex=.8)

پیاده‌سازی درخت تصمیم و جنگل تصادفی با R

مدل اکنون با استفاده از داده‌های تست مورد آزمون قرار گرفته است و می‌توان مشاهده کرد که درصد دسته‌بندی غلط برابر با ٪۱۶.۷۵ است. واضح است که هر چه این میزان کمتر باشد بهتر است، بنابراین این امر از آن حکایت دارد که در حال حاضر مدل در پیش‌بینی «داده‌های واقعی» صحیح‌تر عمل می‌کند.

> #Model Testing
> out <- predict(pdtree)
> table(out[1:193],testData$response)
> response_predicted <- colnames(out)[max.col(out, ties.method = c("first"))] # predicted
> response_input <- as.character (testData$response) # actuals
> mean (response_input != response_predicted) # misclassification %
[1] 0.2844156

حل مساله رگرسیون با درخت تصمیم

هنگامی که متغیرهای وابسته به جای طبقه‌ای، عددی هستند، از درخت رگرسیون به صورت زیر استفاده می‌شود.

> #Regression Tree
fitreg <- rpart(CarSales~Age+Gender+Miles+Debt+Income,
                method="anova", data=inputData)

printcp(fitreg)
plotcp(fitreg)
summary(fitreg) 
par(mfrow=c(1,2)) 
rsq.rpart(fitreg) # cross-validation results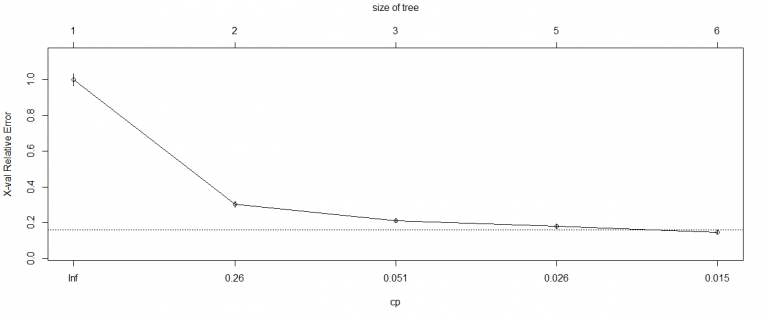

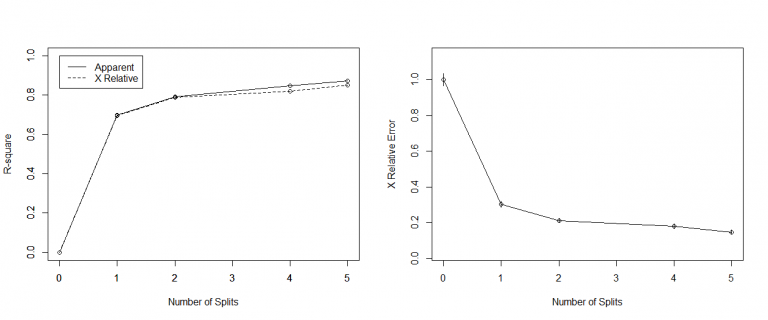
درخت رگرسیون

درخت رگرسیون

> #Regression Tree
> fitreg <- rpart(CarSales~Age+Gender+Miles+Debt+Income,
+                 method="anova", data=inputData)
> 
> printcp(fitreg)

Regression tree:
rpart(formula = CarSales ~ Age + Gender + Miles + Debt + Income, 
    data = inputData, method = "anova")

Variables actually used in tree construction:
[1] Age    Debt   Income

Root node error: 6.283e+10/770 = 81597576

n= 770 

        CP nsplit rel error
1 0.698021      0   1.00000
2 0.094038      1   0.30198
3 0.028161      2   0.20794
4 0.023332      4   0.15162
5 0.010000      5   0.12829
   xerror     xstd
1 1.00162 0.033055
2 0.30373 0.016490
3 0.21261 0.012890
4 0.18149 0.013298
5 0.14781 0.013068

> plotcp(fitreg)
> summary(fitreg)
 
Call:
rpart(formula = CarSales ~ Age + Gender + Miles + Debt + Income, 
    data = inputData, method = "anova")
  n= 770 

          CP nsplit rel error
1 0.69802077      0 1.0000000
2 0.09403824      1 0.3019792
3 0.02816107      2 0.2079410
4 0.02333197      4 0.1516189
5 0.01000000      5 0.1282869
     xerror       xstd
1 1.0016159 0.03305536
2 0.3037301 0.01649002
3 0.2126110 0.01289041
4 0.1814939 0.01329778
5 0.1478078 0.01306756

Variable importance
  Debt  Miles Income    Age 
    53     23     20      4

سپس، با استفاده از کد زیر درخت رگرسیون هرس می‌شود.

> #Prune the Tree
pfitreg<- prune(fitreg, cp=fitreg$cptable[which.min(fitreg$cptable[,"xerror"]),"CP"]) # from cptable   
plot(pfitreg, uniform=TRUE,
     main="Pruned Regression Tree for Sales")
text(pfitreg, use.n=TRUE, all=TRUE, https://blog.faradars.org/wp-admin/post-new.php#cex=.8)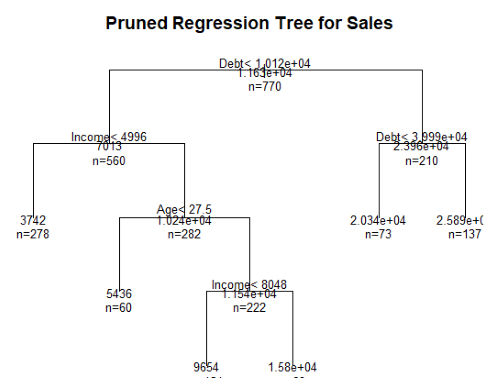

درخت تصمیم و جنگل تصادفی در R

جنگل تصادفی

اگر درخت‌های تصمیم بسیاری وجود داشته باشند که هدف «برازش» (Fit) آن‌ها بدون وقوع «بیش‌برازش» (Overfitting) باشد، یک راهکار برای حل مساله استفاده از «جنگل تصادفی» (Random Forest) است. یک جنگل تصادفی امکان تعیین مهم‌ترین پیش‌بین‌ها را در میان متغیرهای توصیفی با تولید درخت‌های تصمیم زیاد و رتبه‌دهی به متغیرها بر اساس اهمیت آن‌ها فراهم می‌کند.

> library(randomForest)
> fitregforest <- randomForest(CarSales~Age+Gender+Miles+Debt+Income,data=inputData)
> print(fitregforest) # view results

Call:
 randomForest(formula = CarSales ~ Age + Gender + Miles + Debt +      Income, data = inputData) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 10341022
                    % Var explained: 87.33
> importance(fitregforest) # importance of each predictor
       IncNodePurity
Age       5920357954
Gender     187391341
Miles    10811341575
Debt     21813952812
Income   12694331712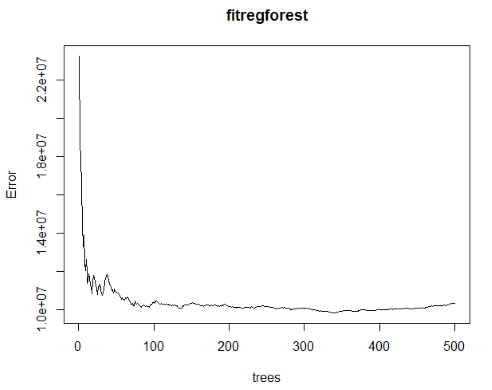

درخت تصمیم و جنگل تصادفی در R

در شکل بالا می توان مشاهده کرد که اعتبار (کارت اعتباری) به عنوان مهم‌ترین عامل علامت‌گذاری شده، در واقع مشتریانی که سطح اعتبار بالاتری دارند احتمال بیشتری دارد که پول بیشتری نیز برای خرید خودرو صرف کنند. می‌توان مشاهده کرد که ٪۸۷.۳۳ از تغییرات به وسیله «جنگل تصادفی» توصیف شده و خطا در تقریبا ۱۰۰ درخت کمینه شده است.

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

^^

بر اساس رای ۹ نفر
آیا این مطلب برای شما مفید بود؟
شما قبلا رای داده‌اید!
اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.
کپی شد
«الهام حصارکی»، فارغ‌التحصیل مقطع کارشناسی ارشد مهندسی فناوری اطلاعات، گرایش سیستم‌های اطلاعات مدیریت است. او در زمینه هوش مصنوعی و داده‌کاوی، به ویژه تحلیل شبکه‌های اجتماعی، فعالیت می‌کند.
مطالب مرتبط

نظر شما چیست؟

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

برچسب‌ها