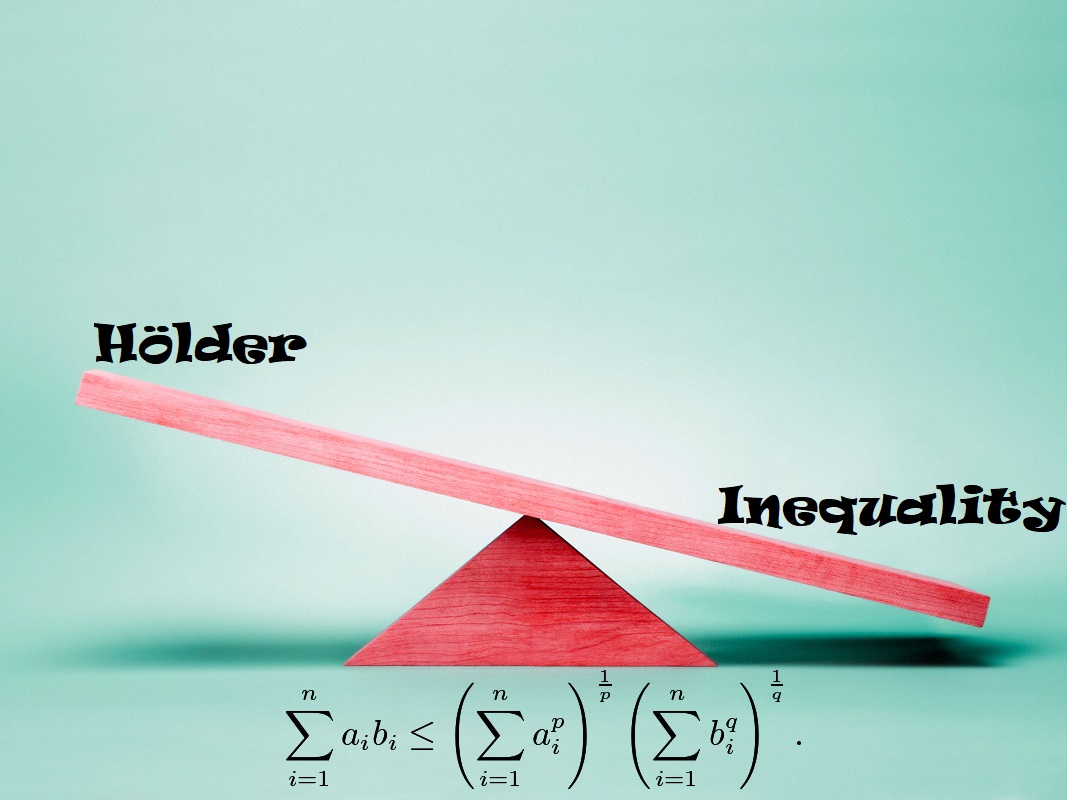
نامساوی هولدر – به زبان ساده
بررسی معادلات روشی برای پیدا کردن ریشه یا مقداری است که تساوی به ازاء آن برقرار میشود. از طرفی تحقیق در مورد نامعادلات نیز برای پیدا کردن کران بالا یا پایین برای یک رابطه ریاضی بسیار موثر هستند. در نوشتار معادله و نامعادله در ریاضی — پیدایش و کاربردها در مورد هر دو این تکنیکها به زبان ساده صحبت شد. نامساویها یا نامعادلههای زیادی در ریاضی وجود دارند که هر یک برای مشخص کردن کرانهای یک رابطه خاص به کار میروند. در این نوشتار با نامساوی هولدر (Holder Inequality) آشنا خواهیم شد و کاربردهای آن را در ریاضیات خواهیم دید.

برای آشنایی بیشتر با انواع نامساویها، نوشتارهای نامساوی مثلثی — به زبان ساده و نامساوی شوارتز — به زبان ساده را بخوانید. همچنین به منظور آگاهی از نحوه ترسیم نامعادلات ریاضی، نوشتار رسم نامعادلات و نامساوی های خطی — به زبان ساده را مطالعه کنید. علاوه بر این موارد خواندن نوشتار تعیین علامت عبارت های جبری و نامساوی ها — به زبان ساده و نیز خالی از لطف نیست.
نامساوی هولدر (Holder Inequality)
در ریاضیات، یکی از نامساویهای پایه و کاربردی در فضای نامساوی هولدر است. این نامساوی به افتخار «اوتو هولدر» (Otto Hölder) ریاضیدان آلمانی، که این نامساوی را در سال 1889 میلادی مورد بررسی قرار داده است، نامساوی هولدر نامیده شده است.

قضیه هولدر
به صورت رسمی نامساوی هولدر که گاهی به آن قضیه هولدر نیز میگویند، به صورت زیر بیان میشود.
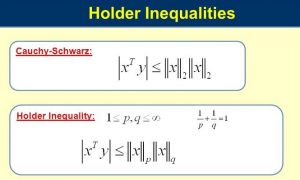
قضیه هولدر: فرض کنید که یک فضای اندازهپذیر (Measurable Space) باشد. همچنین دو مقدار و را مقادیری حقیقی در بازه در نظر بگیرید که رابطه بینشان برقرار است. آنگاه برای هر تابع با مقادیر حقیقی (مختلط) مثل و روی داریم:
نکته: اگر باشد، نامساوی به تساوی تبدیل خواهد شد.
مقادیر و را مزدوجهای هولدر (Holder Conjugates) مینامند. اگر بازه این مقادیر در فاصله قرار بگیرد میتوانیم به جای نُرم (|.|) از انتگرال استفاده کنیم، در این صورت داریم.
نکته: اگر مقدار باشد، نامساوی هولدر به نامساوی کوشی-شوارتز تبدیل خواهد شد. یعنی:
در این صورت تساوی زمانی رخ خواهد داد که باشد.
یکی از کاربردهای مهم برای نامساوی هولدر، اثبات «نامساوی مینکوفسکی» (Minkowski Inequality) است. در حقیقت نامساوی مینکوفسکی، همان نامساوی مثلثی در فضای است.
اثبات قضیه هولدر: قضیه هولدر به چند روش اثبات میشود. در اینجا از روش نامساوی جنسن (Jensen Inequality) استفاده خواهیم کرد. مشخص است که تابع مربع یا با شرط یا تابع محدب است. پس برای هر تابعی مثل داریم:
در نتیجه خواهیم داشت:
حال را یک توزیع احتمال (Probability Distribution) و را یک تابع اندازهپذیر در نظر بگیرید. همچنین فرض کنید یک اندازه (Measure) دلخواه باشد، بطوریکه توزیع ، دارای چگالی متناسب با نسبت به اندازه باشد. یعنی داشته باشیم:
از آنجایی که است، در نتیجه . حال را در نظر میگیریم. به این ترتیب برای خواهیم داشت:
نامساوی آخر از آنجا نتیجه میشود که و . پس در نهایت نتیجه حاصل خواهد شد، یعنی:
نکته: نامساوی هولدر را میتوان برای مشخص کردن یک کران بالا برای انتگرال ضرب دو تابع در نظر گرفت. در این صورت اگر امکان محاسبه انتگرال حاصل ضرب دو تابع وجود نداشته باشد، میتوانیم برای این حاصلضرب یک کران بالا در نظر بگیریم.
کاربردهای نامساوی هولدر
در این قسمت به بعضی از کاربردهای نامساوی هولدر اشاره میکنیم که بخصوص در نظریه اندازه (Measure Theory) مانند نظریه احتمال (Probability Theory) به کار میروند. همچنین در فضای برداری و توابع بردار-مقدار نیز نامساوی هولدر را مورد بررسی قرار خواهیم داد.
نامساوی هولدر برای اندازههای شمارشی
در فضای بُعدی اقلیدسی اگر مجموعه نامتناهی و شمارشپذیر با یک اندازه شمارشی (Counting Measure) در نظر گرفته شود، نامساوی هولدر به صورت زیر در خواهد آمد:
همچنین اگر را مجموعه اعداد طبیعی با یک اندازه شمارشی در نظر بگیریم، نامساوی هولدر به صورت زیر نوشته خواهد شد:
نامساوی هولدر برای توابع بردار-مقدار
فرض کنید فضای یک فضای سیگما-متناهی () بوده و و توابعی -اندازهپذیر با مقادیر حقیقی در فضای بُعدی روی این فضا در نظر گرفته شوند. آنگاه خواهیم داشت:
اگر به جای فضای سیگما-متناهی، فضای متناهی (Finite Space) را در نظر بگیریم، میتوانیم نامساوی هولدر را برای بردارهای متناهی و برای اعداد حقیقی به صورت زیر بنویسیم:
که در آن است و اگر و هر دو مثبت باشند رابطه زیر را هم میتوان نوشت.
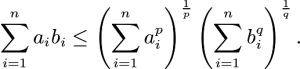
نامساوی هولدر برای اندازه لبگ
اگر مجموعه را یک زیر مجموعه از اعداد حقیقی در فضای بُعدی با اندازه لبگ (Lebesgue Measure) در نظر بگیریم، بطوری که و دو تابع حقیقی-مقدار روی باشند نامساوی هولدر به صورت زیر نوشته خواهد شد.
نامساوی هولدر برای اندازه احتمال
فضای احتمال را در نظر بگیرید. نامساوی هولدر برای عملگر امید ریاضی که همان مقدار مورد انتظار (Expected Value) برای متغیر تصادفی است، براساس فضای القاء شده توسط متغیرهای تصادفی و به صورت زیر درخواهد آمد:
نکته: اگر و باشند، آنگاه مزدوج هولدر خواهد بود. در این صورت میتوان نامساوی زیر را برای گشتاور مرتبه ام نوشت.
بنابراین اگر گشتاور قدر مطلق ام یک متغیر تصادفی، متناهی باشد (وجود داشته باشد) حتما گشتاور قدر مطلق ام که است نیز وجود خواهد داشت. البته این نامساوی را با استفاده از نامساوی جنسن نیز میتوان نشان داد.
نامساوی هولدر تعمیم یافته
اگر یک فضای احتمال (Probability Space) باشند، میتوان فرض کرد که بطوری که باشد. در این صورت نامساوی هولدر به صورت زیر خواهد بود.
بطوری که و توابعی حقیقی یا مختلط و اندازهپذیر روی باشند.
خلاصه و جمعبندی
در این نوشتار با نامساوی هولدر برای اندازههای مختلف صحبت کردیم. همچنین نحوه اثبات آن و حالت تعمیم یافته برای نامساوی هولدر را مرور کردیم. از نامساوی هولدر بخصوص در زمینه محاسبات امید ریاضی در مباحث احتمال و تئوری آمار استفاده میشود. همچنین در تئوری اندازه، برای تعیین کران بالا برای انتگرال ضرب توابع اندازه پذیر نیز از این نامساوی استفاده میشود.
در صورتی که مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی
- آموزش ریاضی عمومی ۲
- مجموعه آموزشهای محاسبات عددی
- نامساوی شوارتز — به زبان ساده
- رسم نامعادلات و نامساوی های خطی — به زبان ساده
- نامساوی های ریاضی — به زبان ساده
^^