نامساوی جنسن (Jensen Inequality) — به زبان ساده
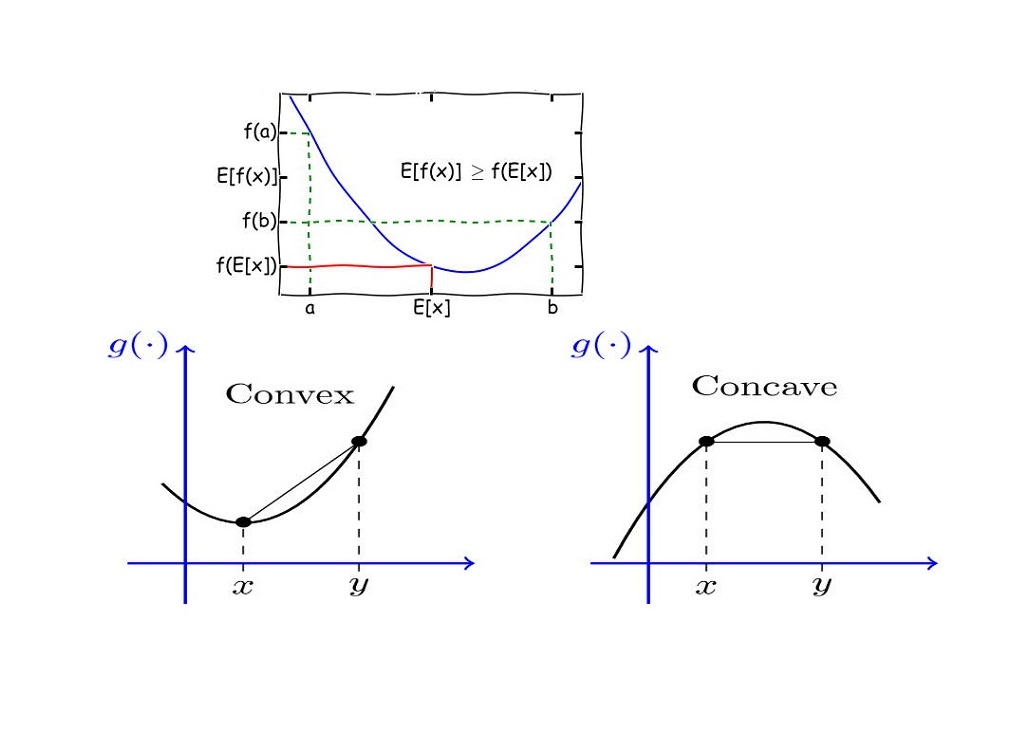
یکی از نامساویهای اصلی در ریاضیات، بخصوص در بررسی نامساویها برای توابع «مقعر» (Concave) و «محدب» (Convex)، نامساوی جنسن (Jensen Inequality) است. این نامساوی به افتخار ریاضیدان دانمارکی «جان جنسن» (John Jensen) نامگذاری شده است که در سال 1906 آن را برای توابع محدب معرفی کرد. بیان صحیح نام این دانشمند در زبان دانمارکی «ینسن» است ولی از آنجا که در کتابهای انگلیسی نامش به صورت «جنسن» خوانده میشود، این نامساوی را بیشتر با تلفظ جنسن به جای ینسن به کار میبرند. هدف او از ابداع این نامساوی، مشخص کردن رابطه بین انتگرال یک تابع محدب با تابعی محدب از یک انتگرال بود. البته امروزه این نامساوی در بسیاری از زمینههای دیگر به غیر از انتگرال نیز به کار میرود.
در ریاضیات به کمک نامساوی جنسن میتوان نشان داد که یک تبدیل محدب روی میانگین همیشه از میانگین آن تبدیل محدب کوچکتر است. البته این امر برای توابع مقعر نیز برعکس است به این معنی که یک تبدیل مقعر روی میانگین همیشه از میانگین آن تبدیل مقعر بزرگتر است. در مباحث آمار و احتمال، بوسیله نامساوی جنسن میتوان نشان داد که همیشه واریانس یک متغیر تصادفی، نامنفی است.
برای آشنایی با دیگر نامساویهای ریاضی میتوانید مطلب نامساوی های ریاضی — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای فضای متریک و نامساوی مثلثی — به زبان ساده و نامساوی شوارتز — به زبان ساده نیز خالی از لطف نیست.
نامساوی جنسن
فرم اصلی نامساوی جنسن دارای اعداد و متغیرهای زیادی است که اگر توسط زبان نظریه اندازه (Measure theory) یا احتمال (Probability) بیان شود، شکل سادهتری خواهد داشت. ابتدا فرم اصلی نامساوی جنسن را بیان میکنیم، سپس با توجه به نظریه اندازه، نامساوی جنسن را معرفی میکنیم.
نامساوی جنسن و دنباله متناهی از مقادیر
فرض کنید $$\phi$$ تابعی محدب (Convex) و اعداد $$x_{1},x_{2},\ldots ,x_{n}$$ نیز در دامنه آن قرار داشته باشند. با انتخاب مقادیر وزن (Weights) $$a_i$$، نامساوی جنسن به فرم زیر نوشته میشود.
$$\large \varphi \left({\frac {\sum a_{i}x_{i}}{\sum a_{i}}}\right)\leq {\frac {\sum a_{i}\varphi (x_{i})}{\sum a_{i}}}$$
رابطه ۱
همچنین اگر تابع $$\phi$$ مقعر باشد این نامساوی به صورت زیر در خواهد آمد.
$$\large \varphi \left({\frac {\sum a_{i}x_{i}}{\sum a_{i}}}\right)\geq {\frac {\sum a_{i}\varphi (x_{i})}{\sum a_{i}}}$$
رابطه ۲
در رابطه ۱ و ۲، تساوی زمانی اتفاق میافتد که $$\large {\displaystyle x_{1}=x_{2}=\cdots =x_{n}}$$ بوده یا تابع $$\phi$$ یک ترکیب خطی از نقاط $${\displaystyle x_{1},x_{2},\cdots ,x_{n}}$$ باشد.
نکته: اگر مقادیر همه وزنها یعنی $$a_i$$ها برابر باشد، رابطه ۱ و ۲ به شکل زیر در خواهند آمد.
$$\large \varphi \left({\frac {\sum x_{i}}{n}}\right)\leq {\frac {\sum \varphi (x_{i})}{n}}$$
رابطه ۳
$$\large {\displaystyle \varphi \left({\frac {\sum x_{i}}{n}}\right)\geq {\frac {\sum \varphi (x_{i})}{n}}}$$
رابطه ۴
مثال 1
فرض کنید $$ {\displaystyle \varphi (x)=\log(x)}$$ باشد. در نتیجه با توجه به مقعر بودن تابع لگاریتم رابطه ۴ به صورت زیر در خواهد آمد.
$$\large {\displaystyle \log \!\left({\frac {\sum _{i=1}^{n}x_{i}}{n}}\right)\geq {\frac {\sum _{i=1}^{n}\log \!\left(x_{i}\right)}{n}}}$$
از طرفی چون تابع نمایی یک تابع یکنوا است میتوانیم دو طرف رابطه بالا را به صورت نمایی بنویسیم و به نامساوی میانگین حسابی و هندسی برسیم. زیرا با بازنویسی رابطه سمت راست بالا خواهیم داشت:
$$\large \log \!\left({\frac {\sum _{i=1}^{n}x_{i}}{n}}\right)\geq \log\left(\prod _{i=1}^{n}x_{i}\right)^{\tfrac{1}{n}}$$
پس
$$\large \quad {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}$$
مثال ۲
فرض کنید $$X$$ یک متغیر تصادفی گسسته باشد. میخواهیم نشان دهیم که واریانس این متغیر تصادفی همیشه نامنفی است. با توجه به شیوه محاسبه واریانس رابطه زیر را میتوان نوشت:
$$\large Var(X)=\operatorname{E}\left(X-\operatorname{E}[X]\right)^2=\operatorname{E}^2[X]-\operatorname{E}[X^2]$$
از آنجایی که تابع $$f(x)=x^2$$ محدب است، پس در نامساوی جنسن صدق میکند. در نتیجه طبق رابطه ۴ خواهیم داشت:
$$\large \operatorname{E}^2[X]\geq \operatorname{E}[X^2]$$
در نتیجه واریانس همیشه نامنفی خواهد بود.
نامساوی جنسن در نظریه اندازه و احتمال
فرض کنید که فضای اندازه $$(\Omega,A\mu)$$ یک فضای احتمال باشد به این معنی که $$\mu(\Omega)=1$$. در این صورت اگر $$g$$ تابع حقیقی و $$\mu$$-اندازهپذیر و $$\varphi$$ نیز یک تابع محدب روی خط اعداد حقیقی باشد، آنگاه نامساوی جنسن را به صورت زیر میتوان نوشت:
$$\large \varphi \left(\int _{\Omega }g\,d\mu \right)\leq \int _{\Omega }\varphi \circ g\,d\mu$$
رابطه ۵
همچنین به عنوان یک کاربرد نامساوی جنسن در آنالیز حقیقی (Real Analysis) به برآورد رابطه زیر میپردازیم:
$$\large \varphi \left(\int _{a}^{b}f(x)\,dx\right),$$
بطوری که $$a,b \in R$$ و $$f:[a,b]\rightarrow R$$ تابعی نامنفی و انتگرالپذیر لبگ است. در این صورت اندازه بلگ روی بازه $$[a,b]$$ لازم نیست برابر با ۱ باشد. هر چند با انتگرالگیری، میتوان این اندازه را در بازه صفر تا یک تغییر مقیاس داد. به این ترتیب نامساوی جنسن به صورت زیر در خواهد آمد.
$$\large {\displaystyle \varphi \left({\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx\right)\leq {\frac {1}{b-a}}\int _{a}^{b}\varphi (f(x))\,dx.}$$
همین نتیجه را نیز برای اندازه احتمال میتوان نوشت. کافی است که فضای احتمال را به صورت $${\displaystyle (\Omega ,{\mathfrak {F}},\operatorname {P} )}$$ در نظر گرفت. آنگاه برای $$X$$ به عنوان یک متغیر تصادفی انتگرالپذیر و تابع محدب $$\phi$$ خواهیم داشت:
$$\large {\displaystyle \varphi \left(\operatorname {E} [X]\right)\leq \operatorname {E} \left[\varphi (X)\right]}$$
رابطه ۶
این نامساوی نیز بیانگر نامنفی بودن واریانس برای یک متغیر تصادفی پیوسته خواهد بود. نظیر این موضوع را برای متغیر تصادفی گسسته در مثال ۲، بررسی کردیم. واضح است که رابطه اخیر از جایگزینی اندازه $$\mu$$ با تابع احتمال $$P$$ و انتگرال نسبت به $$\mu$$ با امید ریاضی E (مقدار مورد انتظار) و $$g$$ با متغیر تصادفی $$X$$ در رابطه ۴، حاصل شده است.
نکته: توجه داشته باشید که تساوی در نامساوی جنسن در این حالت زمانی رخ میدهد که متغیر تصادفی $$X$$، تباهیده بوده یا $$\varphi$$ یک تابع خطی باشد. البته در صورتی که برای $$A\in R$$ به عنوان یک مجموع بورل (Borel Set) داشته باشیم:
$$\large{\displaystyle \Pr(X\in A)=1}$$
و تابع $$\varphi$$ نیز خطی روی $$A$$ باشد، باز هم نامساوی جنسن به تساوی تبدیل خواهد شد. در این صورت تابع $$\varphi$$ و $$A$$ به صورت زیر در رابطه هستند.
$$\large{\displaystyle \varphi (x)=ax+b,\forall x\in A}$$
تفسیر نامساوی جنسن به صورت تصویری
قبل از اینکه به اثبات نامساوی جنسن بپردازیم بهتر است به صورت تصویری و شهودی با این نامساوی بیشتر آشنا شویم. ابتدا تجسمی از یک تابع محدب ارائه میدهیم. به تصویر زیر توجه کنید.
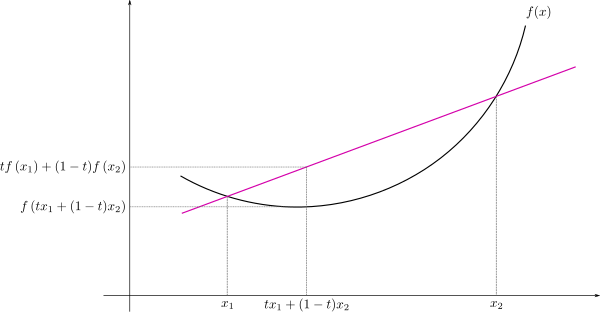
منحنی یا تابع $$f(x)$$ را محدب میگویند اگر خط (وتر) ترسیمی از هر دو نقطه این منحنی بالای قوس آن قرار گیرد. این موضوع را به بیان ریاضی میتوان به صورت زیر نشان داد.
$$\large {\displaystyle f\left(tx_{1}+(1-t)x_{2}\right)\leq tf(x_{1})+(1-t)f(x_{2})}$$
بطوری که $$t\in [0,1]$$ وزن برای نقاط $$x_1$$ و $$x_2$$ و همچنین تابع $$f$$ باشد.
نکته: توجه داشته باشید که برای هر دو نقطه $$x_1$$و $$x_2$$، نقاط بین آنها را میتوان به صورت ترکیب وزندار از آن دو نقطه نوشت. در نتیجه رابطه زیر برقرار است.
$$\large x_1 \leq tx_{1}+(1-t)x_{2} \leq x_2$$
اگر $$t=\tfrac{1}{2}$$ باشد، آنگاه رابطه $$x=tx_{1}+(1-t)x_{2}$$ نقطهای را پدید میآورد که از هر دو نقطه $$x_1$$ و $$x_2$$ فاصله یکسانی دارد. واضح است که با در نظر گرفتن $$t=0$$ نقطه $$x_2$$ و با $$t=1$$ نقطه $$x_1$$ حاصل خواهد شد.
حال به بررسی نامساوی جنسن به صورت تصویری میپردازیم. در شکل زیر براساس مفهوم امید ریاضی و تابع محدب $$\varphi$$، نامساوی جنسن مشخص شده است. مقادیر روی محور افقی مربوط به متغیر تصادفی $$X$$ است. امید ریاضی یا میانگین این مقادیر نیز به صورت $$E\{X\}$$ روی این محور نمایش داده شده است. توجه داشته باشید که منحنی توزیع احتمال $$X$$ و همینطور $$Y$$ مقداری به سمت چپ چولگی دارند. به همین علت میانگین درست روی قله توزیع احتمال قرار نگرفته است.
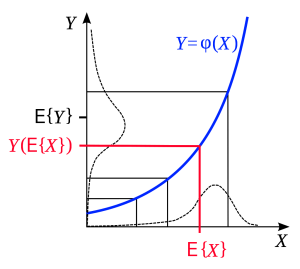
حال تبدیلی به صورت $$Y=\varphi(X)$$ انجام شده و متغیر تصادفی $$Y$$ پدیده آمده است. با اتصال نقطه $$E(x)$$ به منحنی $$\varphi(X)$$ میتوان نگاشت این نقطه را روی محور عمودی نیز مشخص کرد. این نقطه به صورت $$Y(E\{X\})$$ روی این محور نمایش داده شده. ولی براساس نقاط تبدیل یافته، امید ریاضی متغیر تصادفی $$Y$$ که به صورت $$E\{Y\}$$ در محور عمودی قابل مشاهده است از $$Y(E\{X\})$$ بزرگتر است زیرا تابع محدب باعث کشیدگی مقادیر روی محور عمودی میشود.
منحنی توزیع مقادیر $$Y$$ نیز به خوبی ارتباط بین توزیع متغیر تصادفی $$X$$ و $$Y$$ را نشان میدهد. واضح است که پراکندگی و دامنه تغییرات متغیر تصادفی $$Y$$ که تابع محدبی از $$X$$ است بسیار بیشتر از خود متغیر تصادفی $$X$$ است.
در منحنی $$\varphi(X)$$ دیده میشود که به ازاء مقادیر کوچکتر از $$X_0$$، نقاط تابع (مقادیر $$Y$$) از $$X$$ کوچکتر هستند ولی برای $$X>X_0$$ این ارتباط برعکس میشود و نقاط روی محور عمودی دارای طول بیشتری هستند. حال اگر $$X_0$$ را همان امید ریاضی یعنی $$E[X]$$ در نظر بگیریم نامساوی جنسن حاصل میشود.
$$\large {\displaystyle \varphi (\operatorname {E} [X])\leq \operatorname {E} [\varphi (X)]=\operatorname {E} [Y],}$$
و تساوی زمانی رخ میدهد که تابع $$\varphi$$ ترکیب خطی از $$X$$ باشد.
اثبات نامساوی جنسن
برای نامساوی جنسن، اثباتهای مختلف در حوزههای گوناگون وجود دارد در ادامه به اثبات نامساوی جنسن در فضای متناهی اشاره خواهیم کرد.
اثبات براساس تعریف دنباله متناهی
فرض کنید $$\lambda_1$$ و $$\lambda_2$$ دو عدد نامنفی حقیقی باشند بطوری که $$\lambda_1+\lambda_2=1$$ آنگاه برای تابع محدب $$\varphi$$ داریم:
$$\large \forall x_{1},x_{2}:\qquad \varphi \left(\lambda _{1}x_{1}+\lambda _{2}x_{2}\right)\leq \lambda _{1}\,\varphi (x_{1})+\lambda _{2}\,\varphi (x_{2}).$$
واضح است که این نامساوی براساس محدب بودن این تابع نوشته شده است. اگر وزنها را به صورت $$\lambda_1\cdots,\lambda_n$$ در نظر بگیریم، آنگاه با شرط $$\lambda_1 + ... + \lambda_n = 1$$ و برای هر $$x_1,\cdots, x_n$$ خواهیم داشت:
$$\large \varphi (\lambda _{1}x_{1}+\lambda _{2}x_{2}+\cdots +\lambda _{n}x_{n})\leq \lambda _{1}\,\varphi (x_{1})+\lambda _{2}\,\varphi (x_{2})+\cdots +\lambda _{n}\,\varphi (x_{n}),$$
این فرم از حالت متناهی نامساوی جنسن به راحتی بوسیله استقرا اثبات میشود:
- گام اول: با توجه به خاصیت تابع محدب در حالت $$n=2$$، نامساوی جنسن صحیح است.
- گام دوم: فرض کنید این نامساوی برای حالت $$k=n$$ نیز برقرار باشد.
- گام سوم: نشان میدهیم که نامساوی جنسن برای $$k=n+1$$ نیز برقرار است.
از آنجایی که مجموع مقادیر نامنفی فقط زمانی برابر با ۱ میشود که حداقل یکی از آنها مثبت (یا برابر با ۱) باشد، فرض میکنیم $$\lambda_1>0$$ در نتیجه خواهیم داشت:
$$\large {\begin{aligned}\varphi \left(\sum _{i=1}^{n+1}\lambda _{i}x_{i}\right)&=\varphi \left(\lambda _{1}x_{1}+(1-\lambda _{1})\sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}x_{i}\right)\\&\leq \lambda _{1}\,\varphi (x_{1})+(1-\lambda _{1})\varphi \left(\sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}x_{i}\right).\end{aligned}}$$
از آنجایی که $$\lambda_1>0$$ است داریم:
$$\large \sum _{i=2}^{n+1}{\frac {\lambda _{i}}{1-\lambda _{1}}}=1$$
با توجه به گام دوم میتوانیم به استقرا پایان دهیم. در نتیجه:
$$\large \varphi \left(\sum _{i=1}^{n+1}\lambda _{i}x_{i}\right)\leq \lambda _{1}\,\varphi (x_{1})+\dfrac{(1-\lambda_1)}{(1-\lambda_1)}\varphi \left(\sum _{i=2}^{n+1}{\lambda _{i}}x_{i}\right)=\sum_{i=1}^{n+1}\lambda_ix_i$$
نامساوی جنسن تعمیم یافته
فرض کنید متغیر تصادفی $$X$$ تک بُعدی بوده و دارای میانگین و واریانس متناهی است.
$$\large E(X)=\mu, \;\;\;Var(X)=\sigma^2 \geq 0$$
همچنین فرض کنید که تابع $$\varphi$$ دو بار مشتقپذیر بوده و داشته باشیم:
$$\large{\displaystyle h(x)\triangleq {\frac {\varphi \left(x\right)-\varphi \left(\mu \right)}{\left(x-\mu \right)^{2}}}-{\frac {\varphi '\left(\mu \right)}{x-\mu }}.}$$
در نتیجه میتوان نامساوی زیر را در نظر گرفت.
$$\large{\displaystyle \sigma ^{2}\inf {\frac {\varphi ''(x)}{2}}\leq \sigma ^{2}\inf h(x)\leq E\left[\varphi \left(X\right)\right]-\varphi \left(E[X]\right)\leq}$$
$$\large \sigma ^{2}\sup h(x)\leq \sigma ^{2}\sup {\frac {\varphi ''(x)}{2}}$$
رابطه ۷
اگر $$\varphi$$ تابعی محدب باشد، پس $$ {\displaystyle \varphi ''(x)\geq 0} $$ است در نتیجه فرم نامساوی جنسن از رابطه ۷ ساخته خواهد شد.
کاربردهای نامساوی جنسن در آمار
نامساوی جنسن در آمار و احتمالات بسیار به کار گرفته شده است. در این میان میتوان به رابطه نامساوی جنسن برای امید ریاضی (Mathematical Expectation) متغیر تصادفی و همچنین قضیه رائو-بلکول (Rao-Blackwell) اشاره کرد. در ادامه به این موضوعات به عنوان کاربردهایی از نامساوی جنسن خواهیم پرداخت.
نامساوی جنسن برای امید ریاضی متغیر تصادفی
از نامساوی جنسن بخصوص در رابطههایی که برحسب چگالی احتمال نوشته میشود، بسیار استفاده میشود. فرض کنید $$\Omega$$ یک زیر مجموعه اندازهپذیر روی اعداد حقیقی و $$f(x)$$ نیز تابعی نامنفی و حقیقی باشد، بطوری که
$$\large\int _{-\infty }^{\infty }f(x)\,dx=1.$$
در زبان احتمال، چنین تابعی را تابع چگالی احتمال مینامند. در این صورت نامساوی جنسن برای تابع حقیقی-مقدار $$g$$ و محدب $$\varphi$$ به صورت زیر در خواهد آمد.
$$\large\varphi \left(\int _{-\infty }^{\infty }g(x)f(x)\,dx\right)\leq \int _{-\infty }^{\infty }\varphi (g(x))f(x)\,dx.$$
نکته: این فرم همان نامساوی برای امید ریاضی که در رابطه ۶ ذکر شده را هم نتیجه میدهد. کافی است که $$g(x)=X$$ باشد که $$X$$، یک متغیر تصادفی روی فضای احتمال است. پس خواهیم داشت.
$$\large \varphi\left(\operatorname{E}(X)\right)=\varphi \left(\int _{-\infty }^{\infty }g(x)f(x)\,dx\right)\leq \int _{-\infty }^{\infty }\varphi (g(x))f(x)\,dx=\operatorname{E}\left(\varphi(X)\right)$$
نامساوی جنسن و قضیه رائو-بلکول
قضیه رائو-بلکول به منظور انتخاب برآوردگر مناسب برای پارامتر به کار میآید. این قضیه توسط دو دانشمند بزرگ آمار به نامهای «رائو» (Calyampudi Radhakrishna Rao) و «بلکول» (David Blackwell) اثبات و مورد استفاده قرار گرفته است. صورت این قضیه به شکل زیر است.
اگر $$L$$ تابعی محدب و $${\displaystyle {\mathfrak {G}}}$$ یک زیر-سیگما-جبر (Sub-Sigma_algebra) باشد، آنگاه میتوان براساس امیدریاضی شرطی نوشت:
$$\large {\displaystyle L(\operatorname {E} [\delta (X)\mid {\mathfrak {G}}])\leq \operatorname {E} [L(\delta (X))\mid {\mathfrak {G}}]\rightarrow \operatorname {E} [L(\operatorname {E} [\delta (X)\mid {\mathfrak {G}}])]\leq \operatorname {E} [L(\delta (X))].}$$
این نامساوی بیان میکند که اگر $$ \delta(X)$$ برآوردگر پارامتر نامشخص $$\theta$$ به شرط بردار تصادفی $$X$$ باشد، آنگاه توسط آماره بسنده $$T(x)$$ برای $$\theta$$ میتوان برآوردگر $$\delta(x))$$ را بهبود بخشید. به این معنی که برآورد $$\delta(X)$$ به شرط $$T(X)$$ دارای متوسط زیان $$L$$ (ریسک- Risk) کمتری نسبت به $$\delta(X)$$ است.
$$\large {\displaystyle \delta _{1}(X)=\operatorname {E} _{\theta }[\delta (X')\mid T(X')=T(X)],}$$
در اینجا چنین برآوردگری را به صورت $$\delta_1(X)$$ نشان دادهایم.
فیزیک آماری (Statistical Physics)
از نامساوی جنسن در فیزیک آماری در موارد زیادی استفاده میشود بخصوص وقتی که تابع محدب $$g(x)$$ یک تابع نمایی باشد. بر این اساس خواهیم داشت:
$$\large {\displaystyle e^{\operatorname {E} [X]}\leq \operatorname {E} \left[e^{X}\right],}$$
که در آن $$\operatorname{E}$$ همان امید ریاضی برای متغیر تصادفی $$X$$ است. البته اثبات نامساوی جنسن در این حالت بسیار ساده است. کافی است که از نامساوی زیر استفاده کنیم.
$$\large e^X \geq 1 + X $$
حال رابطه راست نامساوی جنسن را باز نویسی میکنیم.
$$\large {\displaystyle \operatorname {E} \left[e^{X}\right]=e^{\operatorname {E} [X]}\operatorname {E} \left[e^{X-\operatorname {E} [X]}\right]}$$
در نتیجه نامساوی جنسن به صورت زیر اثبات میشود.
$$\large e^{E[X]}=e^{E[X]}E\left(e^{X-E[X]}\right)\geq e^{E[X]}E\left(1+X-E[X]-E[X]\right)=\\ \large
e^{E[X]}\times (1+E[X]-E[X])=e^{E[X]}$$
نظریه اطلاع (Information Theory)
فرض کنید که تابع احتمال یا چگالی احتمال اصلی برای متغیر تصادفی $$X$$ به صورت $$p(x)$$ باشد. ولی براساس حدسی برای این تابع چگالی به صورت $$q(x)$$ نیز موجود است. اگر نسبت این دو چگالی را به صورت زیر بنویسیم:
$$\large Y(X) = \frac{q(X)}{p(X)},$$
آنگاه برای تابع محدب $$\varphi(y) = −\log(y) $$ داریم:
$$\large{\displaystyle \operatorname {E} [\varphi (Y)]\geq \varphi (\operatorname {E} [Y])}$$
در نتیجه
$$\large-D(p(x)\|q(x))=\int p(x)\log \left({\frac {q(x)}{p(x)}}\right)\,dx\leq\\ \large \log \left(\int p(x){\frac {q(x)}{p(x)}}\,dx\right)=\log \left(\int q(x)\,dx\right)=0$$
از آنجایی که $$-\log(x)$$ برای مقادیر $$x>0$$ محدب است، تساوی زمانی برقرار است که $$p(x)=q(x)$$ باشد.
چنین نامساوی به «نامساوی گیبز» (Gibbs Inequality) شهرت دارد. همانطور که مشخص است، طرف چپ این نامساوی همان واگرایی کولبک-لیبرل (Kullback-Leibler) برای چگالی $$q$$ و $$p$$ است.
گشتاورهای زوج متغیر تصادفی
متغیر تصادفی $$X$$ را در نظر بگیرید. اگر تابع $$g(x)=x^{2n}$$ باشد، آنگاه
$$\large{\displaystyle {\frac {d^{2}g}{dx^{2}}}(x)=2n(2n-1)x^{2n-2}\geq 0\quad \forall \ x\in \mathbb {R} }$$
و در نتیجه تابع $$g(x)$$ محدب است، پس
$$\large{\displaystyle g(\operatorname {E} [X])=(\operatorname {E} [X])^{2n}\leq \operatorname {E} [X^{2n}].}$$
به بیان دیگر، با توجه به موجود بودن گشتاورهای زوج برای متغیر تصادفی $$X$$ (متناهی بودن گشتاورهای زوج) میتوان نتیجه گرفت که گشتاور اول یعنی $$E(X)$$ نیز متناهی است.
به این ترتیب حتی میتوان برای گشتاورهای مرتبه $$l$$ نیز این موضوع را نشان داد به شرطی که $$ {\displaystyle l\in \mathbb {N}/n } $$ باشد.
نامساوی جنسن در فضای اندازهپذیر شمارشی
فرض کنید اندازه $$\mu$$ در رابطه ۵، یک اندازه شمارشی (Counting Measure) باشد. در این صورت میتوانیم $$\Omega$$ را به صورت $$\Omega=\{x_1,x_2\ldots,x_n\}$$ در نظر بگیریم. در این صورت فرم نامساوی جنسن به شکل زیر نوشته خواهد شد.
$$\large\varphi \left(\sum _{i=1}^{n}g(x_{i})\lambda _{i}\right)\leq \sum _{i=1}^{n}\varphi (g(x_{i}))\lambda _{i},$$
بطوری که ضرایب $$\lambda_i$$ نامنفی هستند و مجموع آنها برابر با واحد است. یعنی $$\lambda_i$$ وزنهای تابع $$g(x)$$ هستند.
$$\large\lambda _{1}+\cdots +\lambda _{n}=1.$$
خلاصه و جمعبندی
در این نوشتار با نامساوی جنسن (Jensen's Inequality) آشنا شدیم. نحوه اثبات و کاربردهای آن نیز بخصوص در فضای احتمال مورد بحث قرار گرفت. از آنجایی که بسیاری از نامساویهای دیگر در احتمال وابسته به نامساوی جنسن است، آگاهی از نحوه به کارگیری آن در شاخههای مختلف از اهمیت زیادی برخوردار است. این نامساوی برای حالتهای مختلف نیز اثبات شد. از این نامساوی برای اثبات رابطه بین میانگین حسابی و میانگین هندسی نیز استفاده میشود، که در این مطلب به این موضوع نیز پرداخته شد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش ریاضی پایه دانشگاهی
- مجموعه آموزشهای ریاضی و فیزیک
- معیار واگرایی کولبک لیبلر (Kullback Leibler)— پیاده سازی در پایتون
- نامساوی های ریاضی — به زبان ساده
- رسم نامعادلات و نامساوی های خطی — به زبان ساده
^^










