رسم نامعادلات و نامساوی‌ های خطی — به زبان ساده

معمولا نمایش هندسی معادلات و نامعادلات در درک روابط بین متغیر و تابع کمک شایانی می‌کند. در این مطلب سعی می‌کنیم برای نامساوی و نامعادلات خطی (مرتبه ۱) روش‌های ترسیم و حل را بررسی کنیم. برای درک بهتر این مطلب بهتر است که ابتدا نوشتار تعیین علامت عبارت های جبری و نامساوی ها — به زبان ساده و معادله خط — به زبان ساده را بخوانید. البته مطالعه مطلب معادله و نامعادله در ریاضی — پیدایش و کاربردها نیز خالی از لطف نیست. توجه داشته باشید که در این نوشتار رسم نامعادلات و نامسوی های خطی را در مختصات دکارتی انجام می‌دهیم.

رسم نامعادلات و نامساوی‌های خطی

ابتدا بهتر است به نمودار یک نامساوی نگاهی بیاندازیم. در زیر نامساوی $$y\leq x+2$$ نمایش داده شده است.

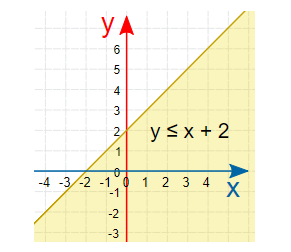
ناحیه‌ای که به رنگ زرد درآمده است، پاسخ برای این نامعادله و یا نامساوی است. خط زرد پررنگ نیز معادله y=x+2 را نشان می‌دهد.

فیلم آموزش المپیاد ریاضی مبحث ترکیبیات – مرحله اول + نکات و حل نمونه سوالات در فرادرس

کلیک کنید

همانطور که دیده می‌شود، یک نامعادله یا نامساوی خطی درست به مانند یک معادله یا تساوی خطی است که به جای علامت تساوی (=) از علامت‌های (>)، (<)، ($$\leq$$) و ($$\geq$$) در آن استفاده شده است.

چگونه نمودار یک نامساوی خطی را رسم کنید؟

برای رسم نامعادلات ابتدا نامساوی را به صورت یک تساوی خطی در نظر گرفته و ترسیم کنید. سپس ناحیه مربوط به نامساوی را روی محور مختصات به صورت سایه‌دار نمایش دهید. به این ترتیب سه گام زیر می‌تواند برای ترسیم چنین نموداری مورد استفاده قرار بگیرد.

1. نامساوی یا نامعادله را به صورتی تنظیم کنید که فقط y در طرف چپ قرار بگیرد و بقیه جملات در سمت راست علامت نامساوی (<, > $$\leq$$, $$\geq$$) دیده شوند.
2. خط مربوط به تساوی یا معادله را ترسیم کنید.
3. ناحیه مربوط به نامساوی را با سایه مشخص کنید به این شکل که اگر نامساوی به صورت $$y\leq$$ باشد، ناحیه سایه‌دار در زیر خط ترسیمی قرار می‌گیرد. اگر نامساوی به صورت $$y\geq$$ باشد، ناحیه سایه‌دار در بالای خط ترسیمی خواهد بود. توجه داشته باشید که اگر نامساوی به صورت اکید (< یا >) باشد، خط ترسیم شده برای تساوی، شامل ناحیه جواب نیستند و باید آن را به صورت خط‌چین در نمودار نمایش داد.

برای روشن‌تر شدن موضوع به حل چند مثال می‌پردازیم.

مثال

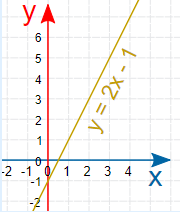
نمودار نامساوی $$y\leq 2x-1$$ را رسم کنید.

گام‌هایی که در بالا به آن اشاره شد را پی‌ می‌گیریم تا نمودار ترسیم شود.

1. مشخص است که نامساوی به صورت استاندارد درآمده است. یعنی y در طرف چپ نامساوی دیده می‌شود و بقیه جملات در سمت راست هستند.
2. خط y=2x-1 را مطابق تصویر زیر ترسیم می‌کنیم.
3. ناحیه پاسخ را با توجه به شرایط گفته شده با سایه نشان می‌دهیم.

از آنجایی که نامساوی به صورت $$\leq$$ نوشته شده است، هنگام رسم نامعادلات ناحیه جواب برای نامساوی در زیر خط ترسیم شده قرار دارد. از طرفی چون نامساوی به صورت کوچکتر یا مساوی است، خط مربوط به تساوی نیز شامل ناحیه جواب است.

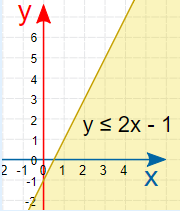
مثال

نامساوی $$2y-x\leq6$$ را ترسیم کنید.

مراحل سه گانه رسم را طی می‌کنیم. ابتدا باید y را به سمت چپ ببریم.

• به دو طرف نامساوی x را اضافه می‌کنیم. $$2y-x+x\leq 6+x$$
• دو طرف نامساوی را به ۲ تقسیم می‌کنیم. $$y\leq \dfrac{6+x}{2}$$ و محاسبات را ساده می‌کنیم. $$y\leq \dfrac{x}{2}+3$$

حال تساوی $$y=\dfrac{2}{2}+3$$ را رسم می‌کنیم.

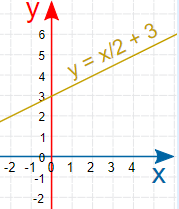
سپس ناحیه پاسخ را سایه می‌زنیم. از آنجایی که نامساوی به صورت $$\leq$$ نوشته شده است، ناحیه در زیر خط ترسیمی قرار دارد و خود خط نیز شامل ناحیه پاسخ است.

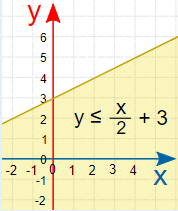
مثال

ناحیه پاسخ نامساوی $$\dfrac{y}{2}+2>x$$ را ترسیم کنید.

باز هم مراحل قبل را تکرار می‌کنیم.

• مقدار ۲ را به طرف دیگر نامساوی می‌بریم یا به هر دو طرف مقدار ۲- را اضافه می‌کنیم. $$\dfrac{y}{2}>x-2$$.
• دو طرف را در ۲ ضرب می‌کنیم. در نتیجه خواهیم داشت $$y>2x-4$$.

از آنجایی نامساوی به صورت اکید است، خط مربوط به تساوی y=2x-۴ را به صورت خط‌چین می‌کشیم.

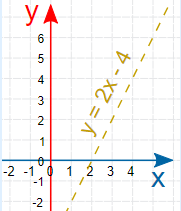
همچنین به علت آن که نامساوی به صورت < است، ناحیه بالای خط‌چین را سایه‌دار می‌کنیم. به این ترتیب ناحیه پاسخ نامعادله طبق تصویر زیر مشخص می‌شود.

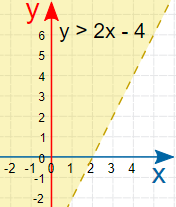
نکته: مشخص است که خط‌چین بیانگر آن است که ناحیه پاسخ شامل خود خط نیست.

حالات خاص

گاهی ممکن است که هنگام رسم نامعادلات ناحیه جواب به صورت یک مستطیل در آید که شامل ناحیه‌ای است که در زیر یک خط افقی یا عمودی قرار دارد.

فیلم آموزش کاربرد مشتق در ریاضیات (برای مدیریت، حسابداری و اقتصاد) (رایگان) در فرادرس

کلیک کنید

فرض کنید نامساوی یا نامعادله به صورت y<4 نوشته شده است. مشخص است که این نامساوی فقط برحسب y نوشته شده و باید ابتدا خط y=4 ترسیم شده و ناحیه زیر این خط به صورت سایه‌دار درآید. تصویر زیر این حالت را به خوبی نشان می‌دهد. از آنجایی که نامساوی به صورت اکید نوشته شده، خط y=4 شامل ناحیه پاسخ نیست و به صورت خط‌چین رسم شده است.

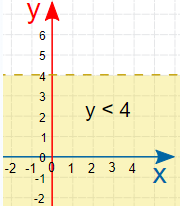
حالت دیگر زمانی  است که نامساوی برحسب فقط x نوشته شده است. برای مثال اگر نامساوی به صورت $$x\geq1$$ باشد ابتدا خط x=1 را رسم می‌کنیم. این خط، عمود بر محور افقی است و از نقطه ۱ روی آن محور عبور می‌کند. مشخص است که به علت علامت $$\geq$$ خط ترسیم شده نیز باید شامل ناحیه پاسخ باشد. به این ترتیب، روی محورهای مختصات، مجموعه مقادیری را مشخص می‌کنیم که دارای طولی بزرگتر از ۱ هستند یا در سمت راست خط x=1 قرار دارند. در زیر نمودار مربوط به این نامساوی ترسیم شده است.

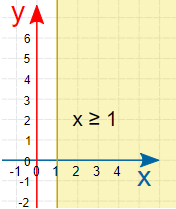
در صورت علاقه‌مندی به مباحث مرتبط در زمینه‌ی ریاضیات، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های ریاضی و فیزیک
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• چندجمله‌ای‌ها – به زبان ساده
• معادله های پارامتری — به زبان ساده
• پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
• معادلات و نامعادلات ریاضی — پیدایش و کاربردها
• معادلات خطی (Linear Equations) — به زبان ساده
• معادله درجه دو — به زبان ساده
• قضیه اساسی جبر — به زبان ساده

^^