نامساوی لگاریتمی – به زبان ساده

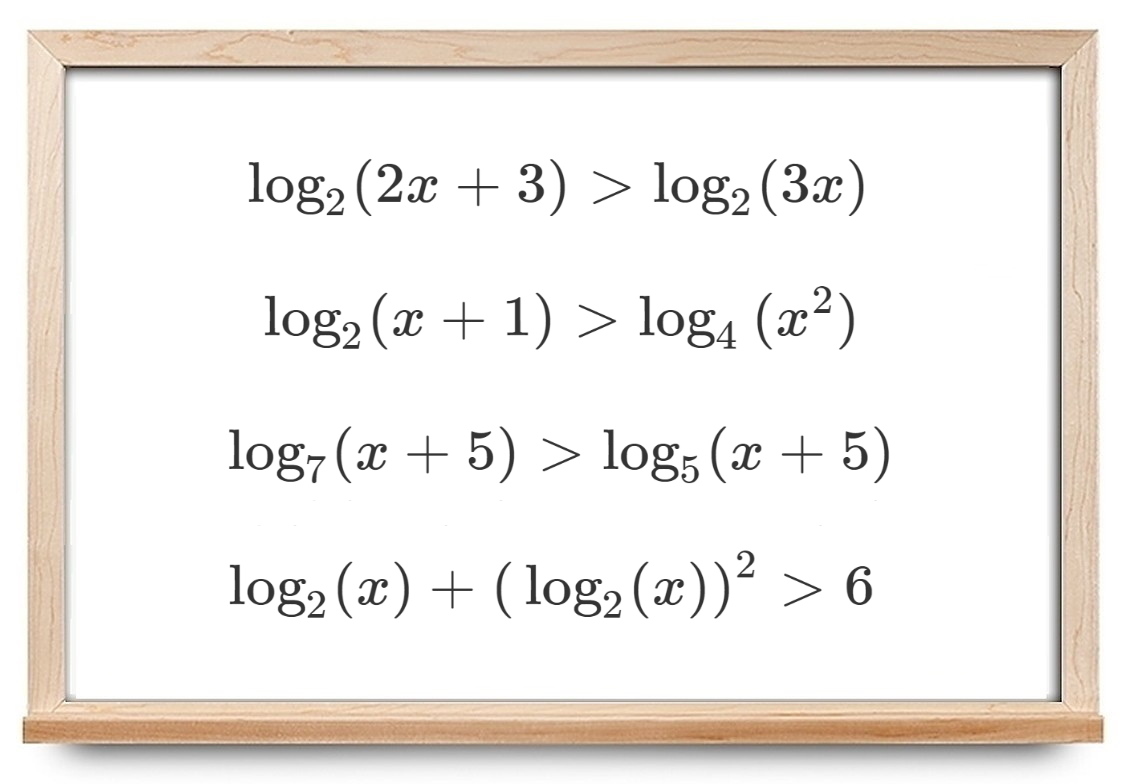
نامساوی لگاریتمی دسته‌ای از نامساوی‌ها است که یک (یا دو) طرف آن با یک عبارت لگاریتمی درگیر است. مشابه نامساوی‌های نمایی، این نامساوی‌ها در تحلیل موقعیت‌هایی که با ضرب مکرر درگیر هستند کاربرد دارند، مانند نرخ بهره و واپاشی.

نامساوی لگاریتمی

نکته اصلی کار با نامساوی لگاریتمی واقعیت زیر است:

اگر $$a > 1$$ و $$x > y$$ باشد، آنگاه $$\log_ax>\log_ay$$. در غیر این صورت، اگر $$0 < a < 1$$ باشد، خواهیم داشت: $$\log_ax<\log_ay$$.

البته پایه لگاریتم نمی‌تواند ۱ یا غیرمثبت باشد. مهم‌تر اینکه، عبارت زیر صحیح است:

اگر $$a > 1$$ و $$\log _ a x > \log _ a y$$، آنگاه $$x > y$$ است. در غیر این‌صورت، اگر $$0 < a < 1$$، آنگاه $$x < y$$.

به بیان رسمی‌تر، تابع لگاریتمی $$f ( x ) = \log _ a x$$ برای $$a > 1$$ یکنوای صعودی (افزایش $$x$$ همواره سبب افزایش $$f ( x )$$ می‌شود) و برای $$0 < a < 1$$ یکنوای نزولی (افزایش $$x$$ موجب کاهش $$f ( x )$$ می‌شود) است.

خوشبختانه، دو عبارتی را که بیان کردیم کاملاً شهودی هستند. وقتی پایه بزرگ‌تر از ۱ باشد، طرفی با آرگومان بزرگ‌تر بزرگ‌تر خواهد بود و عکس آن نیز برای وقتی پایه کوچک‌تر از ۱ باشد، برقرار است. برای مثال، بدون هر دانشی از گزاره‌های فرمول‌بندی شده بالا، به طور شهودی انتظار داریم $$\log _ 2 100$$ بزرگ‌تر از $$\log _ 2 95$$ باشد.

همچنین، نکته مهم زیر را به خاطر بسپرید:

آرگومان لگاریتم باید مثبت باشد.

بنابراین، هر نامساوی از آرگومان‌ها باید مثبت باشد؛ برای مثال، یک نامساوی دارای جمله $$\log _ 2 ( 2 x - 3 )$$ باید شرط $$x > \frac {3}{2}$$ را داشته باشد.

نامساوی لگاریتمی با پایه مشابه

وقتی هر دو سمت یک نامعادله پایه مشابه داشته باشند، مستقیماً می‌توان از گزاره‌های ابتدای متن استفاده کرد.

مثال ۱: چه مقادیری از $$x$$ در نامعادله زیر صدق می‌کنند؟

$$\large \log _ 2 ( 2 x + 3 ) > \log _ 2 ( 3 x )$$

حل: از آنجا که پایه ۲ و بزرگ‌تر از ۱ است، نامعادله $$\log _ 2 ( 2 x + 3 ) > \log _ 2 ( 3 x )$$ نتیجه می‌دهد که $$2 x + 3 > 3 x$$ است. با کم کردن $$2 x$$ از دو طرف نامعادله، به نامساوی $$3 > x$$ می‌رسیم.

علاوه بر این، آرگومان‌های هر دو لگاریتم باید مثبت باشند؛ بنابراین، $$3 x > 0$$ و $$2 x + 3 > 0$$ را نیز داریم. اولی محدودکننده‌تر است، زیرا $$x > 0$$. بنابراین، جواب نهایی $$0 < x < 3$$ خواهد بود.

مفاهیم بالا را می‌توان به عبارات پیچیده‌تری نیز اعمال کرد.

مثال ۲: مقادیر $$x$$ را که در نامساوی زیر صدق می‌کنند، تعیین کنید.

$$\large \log _ 2 \big ( \log _ 3 ( 4 x + 1 ) \big ) > \log _ 2 \big ( \log _ 3 ( 2 x + 3 ) \big )$$

حل: از آنجا که پایه برابر با ۲ و بزرگ‌تر از ۱ است، نامساوی $$\log _ 3 ( 4 x + 1 ) > \log _ 3 ( 2 x + 3 )$$ را خواهیم داشت که خود به $$4x+1>2x+3$$ یا $$2 x > 2 \implies x > 1$$ می‌انجامد. بنابراین، $$x$$ باید بزرگ‌تر از ۱ باشد.

علاوه بر این، آرگومان‌های همه لگاریتم‌ها باید مثبت باشند، اما این در واقع حالتی است که $$x$$ بزرگ‌تر از ۱ است. بنابراین، مجموعه جواب $$x > 1$$ است.

نامساوی لگاریتمی با پایه کوچک‌تر از یک

در این حالت که پایه کوچک‌تر از ۱ است، آنچه پیش‌تر گفتیم اساساً برعکس می‌شود. اکنون طرف بزرگ‌تر آنی است که نمای کوچک‌تری دارد.

مثال ۱:‌ جواب نامعادله زیر را به دست آورید.

$$\large \log _ { \frac { 1 } { 2 } } ( 3 x ) > \log _ { \frac { 1 } { 2 } } ( 2 x + 3 )$$

در اینجا پایه $$\frac 12$$ است که کوچک‌تر از ۱ بوده و منجر به نامساوی $$3 x < 2 x + 3$$ می‌شود. در نتیجه، $$x < 3$$ خواهد بود.

علاوه بر این، آرگومان هر لگاریتم باید مثبت باشد، بنابراین، $$3 x > 0$$ و $$2 x + 3 > 0$$ است. بنابراین، جواب نهایی $$0 < x < 3$$ خواهد بود.

نامساوی لگاریتمی با پایه متفاوت

در بسیاری از نامساوی‌ها، پایه‌ها متفاوت هستند، اما می‌توان آن‌ها را برحسب پایه‌های مشابه بازنویسی کرد. مثال‌های زیر این موضوع را به خوبی نشان می‌دهند.

مثال ۱: نامعادله زیر را حل کنید.

$$\large \log _ 2 ( x + 1 ) > \log _ 4 \big ( x ^ 2 \big )$$

حل: در اینجا پایه‌ها متفاوت‌اند، اما با $$4 = 2 ^ 2$$ با هم ارتباط دارند. نامعادله را به صورت زیر بازنویسی می‌کنیم (تبدیل مبنای ۲ به ۴):

$$\large \log _ 4 \big ( ( x + 1 ) ^ 2 \big ) > \log _ 4 \big ( x ^ 2 \big )$$

بنابراین، $$( x + 1 ) ^ 2 > x ^ 2$$ است و در نتیجه، $$2 x + 1 > 0 \implies x > - \frac { 1 } { 2 }$$. علاوه بر این، آرگومان‌های هر لگاریتم باید مثبت باشند، به جز برای $$x = 0$$. بنابراین، جواب نهایی $$x > - \frac 12$$ و $$x \neq 0$$ است.

مثال ۲: مقادیر $$x$$ را که در نامعادله زیر صدق می‌کنند به دست آورید:

$$\large \log _ 2 ( x ) > \log _ 2 ( 3 ) + \log _ 4 ( 2 5 ) + \log _ 8 ( 3 4 3 )$$

حل: پایه همه لگاریتم‌ها را به ۲ تبدیل می‌کنیم:

$$\large \begin {aligned} \log _ 2 ( x ) & > \log _ 2 ( 3 ) + \log _ 2 ( 5 ) + \log _ 2 ( 7 ) \\ \Rightarrow \log _ 2 ( x ) & > \log _ 2 ( 1 0 5 ) , \end {aligned}$$

بنابراین، $$x > 105$$ است. همه $$x$$های بزرگ‌تر از ۱۰۵ در این نامعادله صدق می‌کنند.

وقتی پایه‌ها متفاوت باشند و نتوان آن‌ها را از طریق یک پایه مشترک با هم مرتبط کرد، استفاده از از فرمول تغییر مبنا ضروری خواهد بود.

مثال ۳: مقادیر $$x$$ را که در نامعادله زیر صدق می‌کنند، به دست آورید.

$$\large \log _ 7 (x + 5 ) > \log _ 5 ( x + 5 )$$

با تغییر مبنا، نامعادله به صورت زیر در می‌آید:

$$\large \frac { \log ( x + 5 ) } { \log 7 } > \frac { \log ( x + 5 ) } { \log 5 } .$$

این نامساوی وقتی $$\log ( x + 5 )$$ منفی باشد، کاملاً صحیح است. بنابراین، خواهیم داشت:

$$\large \log ( x + 5 ) < 0 \implies x + 5 < 1 \implies x < - 4$$

و از آنجا که $$x + 5$$ باید مثبت باشد، نامساوی $$x > - 5$$ را خواهیم داشت. در نهایت، جواب مسئله $$- 5 < x < - 4$$ است.

نامساوی لگاریتمی با چند عبارت

در حالتی که چند عبارت داشته باشیم، بهتر است که متغیر دیگری را به یک عبارت لگاریتمی اختصاص دهیم، نامساوی حاصل را حل کرده و سپس با نامساوی تک‌جمله کار کنیم.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

مثال ۱: نامعادله زیر را حل کنید:

$$\large \log _ 2 ( x ) + \big ( \log _ 2 ( x ) \big ) ^ 2 > 6$$

حل: متغیر $$y = \log _ 2 ( x )$$ را در نظر بگیرید. بنابراین، $$y + y ^ 2 > 6$$ را خواهیم داشت. این نامساوی را می‌توان به صورت $$y ^ 2 + y - 6 = (y - 2 ) ( y + 3 ) > 0$$ بازآرایی کرد که برای $$y > 2$$ یا $$y < - 3$$ صحیح است.

بنابراین:

$$\large \log _ 2 ( x ) > 2 \implies \log _ 2 ( x ) > \log _ 2 4 \implies x > 4$$

یا

$$\large \log _ 2 ( x ) < - 3 \implies \log _ 2 ( x )< \log _ 2 \left ( \frac { 1 } { 8 } \right ) \implies x < \frac { 1 } { 8 } .$$

در نتیجه، جواب نهایی $$0 < x < \frac 1 8$$ و $$x > 4$$ خواهد بود، زیرا آرگومان لگاریتم باید مثبت باشد.

مثال ۲: نامعادله زیر را حل کنید:

$$\large \log _ { \frac { 1 } { 2 } } ( x + 2 ) < - 2 < \log _ { \frac { 1 } { 4 } } ( 2 x )$$

حل: نامعادله اول $$\log_{\frac{1}{2}}(x+2)<-2$$ یا $$\log _ { \frac { 1 } { 2 } } ( x + 2 ) < \log _ { \frac { 1 } { 2 } } ( 4 )$$ است. از آنجا که پایه $$\frac 12$$ کوچک‌تر از یک است، $$x + 2 > 4$$ و در نتیجه، $$x > 2$$ را خواهیم داشت.

نامساوی دوم، $$- 2 < \log _ { \frac { 1 } { 4 } } ( 2 x )$$ یا $$\log _ { \frac { 1 } { 4 } } ( 16 ) < \log _ { \frac { 1 } { 4 } } ( 2 x )$$ است. باز هم مبنا کوچک‌تر از ۱ است، بنابراین، $$16 > 2 x$$ یا $$8 > x$$ را خواهیم داشت.

در نهایت، $$2 < x < 8$$ خواهد بود. از آنجا که آرگومان هر لگاریتم در این بازه مثبت است، جواب نهایی $$2 < x < 8$$ می‌شود.

حل مسائل نامساوی لگاریتمی

دقت کنید که نمای یک لگاریتم می‌تواند کوچک‌تر از یک باشد و به صورت زیر آن را نوشت:

$$\large \large \log _ a b = - \log _ { \frac { 1 } { a } } b$$

مثال ۱: نامساوی لگاریتمی زیر را حل کنید.

$$\large \log _ { \frac { x + 4 } { 2 } } \left ( \log _ { 2 } \frac { 2 x - 1 } { 3 + x } \right ) < 0 .$$

حل: ابتدا، پایه باید مثبت بوده و برابر با ۱ نباشد. بنابراین، $$x > - 4$$ و $$x \neq - 2$$ است. به طور مشابه، آرگومان $$\log _ 2 \frac { 2 x - 1 } { 3 + x }$$ باید مثبت باشد، یعنی $$\frac {2 x - 1 } { x + 3 } > 0 \implies x > \frac 1 2$$ یا $$x < - 3$$. در نتیجه، تنها مقادیر ممکن برای $$x$$، در بازه $$x > \frac 12$$ یا $$- 4 < x < - 3$$ قرار دارد.

اکنون دو حالت زیر را در نظر بگیرید:

حالت اول. $$0 < \frac { x + 4} { 2 } < 1 \iff - 4 < x < - 2$$

در این حالت، لازم است $$\log_2\frac{2x-1}{3+x}>1$$ یا $$\frac{2x-1}{3+x}>2$$ را داشته باشیم که در نتیجه، $$\frac{2x-1}{3+x}-2=\frac{-7}{3+x}>0$$ خواهد بود. بنابراین، $$3 + x$$ منفی است و به عبارت دیگر، $$x < - 3$$.

به یاد داشته باشید که این استراتژی تفریق دو طرف به جای ضرب، از انجام کارهایی که با ضرب سر و کار دارند جلوگیری می‌کند.

حالت دوم. $$\frac { x + 4 } { 2 } > 1 \iff x > - 2$$

در این حالت، لازم است $$\log_2\frac{2x-1}{3+x}<1$$ یا $$\frac{2x-1}{3+x}<2$$ را داشته باشیم، که منجر به نامساوی $$\frac{2x-1}{3+x}-2=\frac{-7}{3+x}<0$$ می‌شود. این زمانی صحیح است، که $$x > - 2$$ باشد.

البته، از قبل می‌دانیم تنها $$x > \frac 12$$ یا $$- 4 < x < - 3$$ ممکن است صحیح باشند و همه $$x$$های $$x > \frac 12$$.

بنابراین، مجموعه جواب به صورت زیر است:

$$\large x > \frac 1 2 , \ - 4 < x < - 3 .$$

یک استراتژی حل مسئله استفاده از فرمول تغییر مبنا است تا همه لگاریتم‌ها مبنای یکسان داشته باشند. این امر استفاده از نامساوی‌های دیگر، مانند میانگین حسابی هندسی را آسان‌تر می‌کند.

مثال ۲: نشان دهید نامساوی زیر برای همه اعداد صحیح $$n \ge 2$$ برقرار است:

$$\large \log _ n ( n + 1 ) > \log _ { n + 1 } ( n + 2 )$$

حل: با استفاده از تغییر مبنا، خواهیم داشت:

$$\large \begin {aligned} \log _ n ( n + 1 ) > \log _ { n + 1 } ( n + 2 ) & \iff \frac { \log ( n + 1 ) } { \log n } > \frac { \log ( n + 2 ) } { \log ( n + 1 ) } \\ & \iff \big ( \log ( n + 1 ) \big )^ 2 > \log n \log ( n + 2 ) . \end {aligned}$$

ضرب لگاریتم‌ها نشانه‌ای برای استفاده از نامساوی میانگین حسابی هندسی است،‌ زیرا جمع مجموع لگاریتم‌ها بسیار ساده است.

بنابراین، داریم:

$$\large \frac { \log n + \log ( n + 2 ) } { 2 } \geq \sqrt { \log n \log ( n + 2 ) } \implies \frac { \log \big ( n ( n + 2 ) \big ) } { 2 } \geq \sqrt { \log n \log ( n + 2 ) } .$$

نامساوی زیر را نیز می‌توان نوشت:

$$\large \log \big ( n( n + 2 ) \big ) = \log \big ( n ^ 2 + 2 n \big ) < \log ( n ^ 2 + 2 n + 1 ) = \log \big ( ( n + 1 ) ^ 2 \big ) = 2 \log ( n + 1 )$$

خواهیم داشت:

$$\large \log ( n + 1) > \frac { \log \big ( n ( n + 2 ) \big ) } { 2 } \geq \sqrt { \log n \log ( n + 2 ) } .$$

بنابراین، نتیجه می‌گیریم:

$$\large \big ( \log ( n + 1 ) \big ) ^ 2 > \log n \log ( n + 2 )$$

که نامساوی اصلی را اثبات می‌کند.