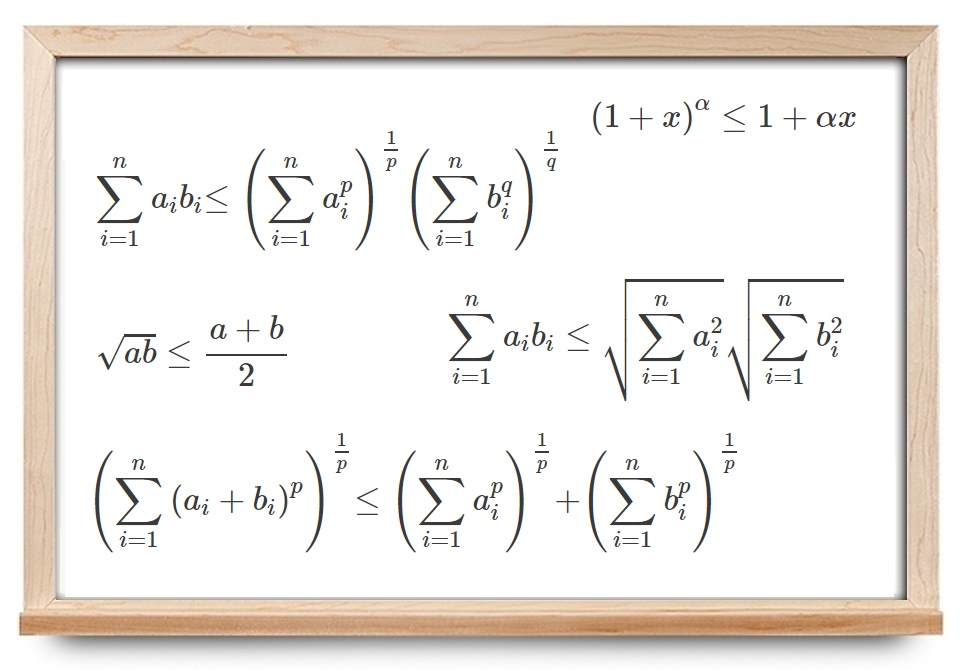نامساوی های ریاضی — به زبان ساده

در میان تمام نامساوی‌‌ها، تعدادی نامساوی کلاسیک معروف وجود دارد که بسیاری از آن‌ها توسط ریاضیدانان مشهور اثبات و با نام آن‌ها نام‌‌گذاری شده‌‌اند. در این آموزش، به معرفی و اثبات برخی از این نامساوی های ریاضی شامل نامساوی‌‌های برنولی، یانگ، هولدر، کوشی-شوارتز و مینکوفسکی خواهیم پرداخت.

رابطه نامساوی های ریاضی

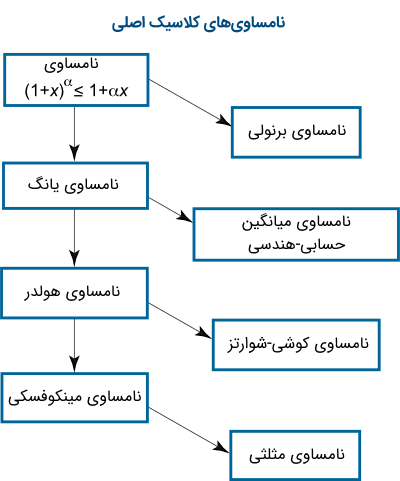
روابط بین نامساوی‌‌های کلاسیک اصلی را می‌‌توان در یک نمودار درختی نشان داد (شکل 1).

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

این نمودار نشان می‌‌دهد که برای مثال، نامساوی کوشی-شوارتز از نامساوی هولدر نتیجه می‌‌شود. در ادامه، نگاهی دقیق‌‌تر به هر یک از نامساوی‌‌های نشان داده شده در نمودار می‌‌اندازیم.

نامساوی $$\LARGE {\left( {1 + x} \right)^\alpha } \le 1 + \alpha x$$ و نامساوی برنولی

نامساوی $${\left( {1 + x} \right)^\alpha } \le 1 + \alpha x$$ که در آن، $$x \ge -1$$ و $$0 \lt \alpha \lt 1$$، منبعی برای استخراج بسیاری از نامساوی‌‌های کلاسیک است.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

این نامساوی را می‌‌توان با استفاده از مشتق اثبات کرد. تابع زیر را در نظر بگیرید:

$$\large f\left( x \right) = {\left( {1 + x} \right)^\alpha } – \alpha x – 1$$

که در آن، $$x \ge -1$$. با مشتق گرفتن از این تابع داریم:

$$\large { f’ \left ( x \right ) = { \left [ { { { \left ( { 1 + x } \right ) } ^ \alpha } – \alpha x – 1 } \right ] ^ \prime } } = { \alpha { \left ( { 1 + x } \right ) ^ { \alpha – 1 } } – \alpha } = { \alpha \left [ { { { \left ( { 1 + x } \right ) } ^ { \alpha – 1 } } – 1 } \right ] . }$$

همانطور که دیده می‌‌شود، در $$x=0$$ مشتق برابر با صفر است. علامت مشتق چپ و راست نقطه $$x=0$$ به مقدار $$\alpha$$ بستگی دارد:

1. اگر $$0 \lt \alpha \lt 1$$ باشد، علامت $$f’\left( x \right)$$ هنگام گذر از نقطه $$x=0$$ از مثبت به منفی تغییر می‌‌کند. در این حالت، در $$x=0$$ یک ماکزیمم داریم.
2. اگر $$\alpha \lt 0$$ یا $$\alpha \gt 1$$ باشد، علامت $$f’\left( x \right)$$ هنگام گذر از نقطه $$x=0$$ از منفی به مثبت تغییر می‌‌کند. از این رو، در این نقطه یک مینیمم خواهیم داشت.

بنابراین، هنگامی که $$x \gt -1$$ است، تابع $$f(x)$$ در حالت 1 نزولی و در حالت 2 صعودی است. در نظر داشته باشید که تابع $$f(x)$$ در $$x=0$$ برابر با صفر است. پس در صورتی که $$x \ge -1$$ باشد، نامساوی‌‌های زیر برقرارند:

1. $$f\left( x \right) \le 0$$ به ازای $$0 \lt \alpha \lt 1$$
2. $$f\left( x \right) \ge 0$$ به ازای $$\alpha \lt 0$$ یا $$\alpha \gt 1$$

یا

1. $${\left( {1 + x} \right)^\alpha } – \alpha x – 1 \le 0$$ به ازای $$0 \lt \alpha \lt 1$$
2. $${\left( {1 + x} \right)^\alpha } – \alpha x – 1 \ge 0$$ به ازای $$\alpha \lt 0$$ یا $$\alpha \gt 1$$

در حالت اول (هنگامی که $$0 \lt \alpha \lt 1$$ است)، نامساوی بالا را می‌‌توان به صورت زیر نوشت:

$$\large { \left ( { 1 + x } \right ) ^ \alpha } \le \alpha x + 1 .$$

از این رابطه برای اثبات سایر نامساوی‌‌های کلاسیک استفاده می‌‌شود.

در حالت دوم (هنگامی که $$\alpha \lt 0$$ یا $$\alpha \gt 1$$ است)، نامساوی زیر را خواهیم داشت:

$$\large { \left ( { 1 + x } \right ) ^ \alpha } \ge \alpha x + 1 .$$

در حالت خاص، اگر فرض کنیم $$\alpha$$ یک عدد طبیعی باشد، آنگاه نامساوی معروف برنولی را به دست خواهیم آورد:

$$\large { { \left ( { 1 + x } \right ) ^ n } \ge 1 + n x , \; \; \; \text {} } \; \; \; \kern-0.3pt { x \ge – 1 , \; n \in \mathbb { N } . }$$

نامساوی یانگ

برای به دست آوردن نامساوی یانگ از نامساوی $${ \left ( { 1 + x } \right ) ^ \alpha } \le \alpha x + 1$$ که به ازای $$x \ge -1$$ و $$0 \lt \alpha \lt 1$$ برقرار است، کمک می‌‌گیریم.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

ابتدا از نمادگذاری زیر استفاده می‌‌کنیم:

$$\large { 1 + x = \frac { a } {b } , } \; \; \; \kern-0.3pt { \alpha = \frac { 1 } { p } , } \; \; \; \kern-0.3pt { \frac { 1 } { q } = 1 – \frac { 1 } { p } . }$$

فرض می‌‌کنیم که $$a \ge 0$$ و $$b \gt 0$$ باشد. از شرط $$0 \lt \alpha \lt 1$$ نیز نتیجه می‌‌شود که $$p \gt 1$$.

با جایگذاری این روابط در نامساوی بالا، داریم:

$$\large { { \left ( { \frac { a } { b } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } \le 1 + \frac { 1 } { p } \left ( { \frac { a } { b } – 1 } \right ) , \; \; } \\ \large \Rightarrow { \frac { { { a ^ { \large \frac { 1 } { p } \normalsize } } } }{ { { b ^ { \large \frac { 1 } { p } \normalsize } } } } \le 1 – \frac { 1 } { p } + \frac { 1 } { p } \frac { a } { b } , \; \; } \Rightarrow { \frac { { { a ^ { \large \frac { 1 } { p } \normalsize } } } } { { { b ^ { \large \frac { 1 } { p } \normalsize } } } } \le \frac { 1 } { q } + \frac { 1 } { p } \frac { a } { b } . }$$

طرفین نامساوی حاصل را در $$b$$ ($$b>0$$) ضرب می‌‌کنیم. در نتیجه، خواهیم داشت:

$$\large { { a ^ { \large \frac { 1 } { p } \normalsize } } { b ^ { 1 – \large \frac { 1 } { p} \normalsize } } \le \frac { a } { p } + \frac { b } { q } , \; \; } \Rightarrow { { a ^ { \large \frac { 1 } { p } \normalsize } } { b ^ { \large \frac { 1 } { q } \normalsize } } \le \frac { a } { p } + \frac { b } { q } . }$$

این نامساوی، همان نامساوی یانگ است.

با قرار دادن $${a^{\large\frac{1}{p}\normalsize}} \to a$$ و $${b^{\large\frac{1}{q}\normalsize}} \to b$$، می‌‌توانیم نامساوی یانگ را به شکل زیر بنویسیم:

$$\large { a b \le \frac { { { a ^ p } } } { p } + \frac { { { b ^ q } } } { q } } \; \; \; \kern-0.3pt { \left ( { p \gt 1 } \right ) . }$$

توجه داشته باشید که به ازای $$p \lt 1$$، نامساوی یانگ به صورت زیر خواهد بود:

$$\large { a b \ge \frac { { { a ^ p } } } { p } + \frac { { { b ^ q } } } { q } } \; \; \; \kern-0.3pt { \left ( { p \lt 1 , \, p \ne 0 } \right ) . }$$

نامساوی میانگین حسابی-هندسی

با قرار دادن $$p = q = {\large\frac{1}{2}\normalsize}$$ در نامساوی یانگ، می‌‌توان نامساوی میانگین‌‌های حسابی و هندسی برای دو عدد نامنفی را به دست آورد:

$$\large { { a ^ { \large \frac { 1 } { 2 } \normalsize } } { b ^ { \large \frac { 1 } { 2 } \normalsize } } \le \frac { a } { 2 } + \frac { b } { 2 } } \; \; \kern-0.3pt { \text {or} \; \; \sqrt { a b } \le \frac { { a + b } } { 2 } . }$$

در حقیقت، می‌‌توان نامساوی یانگ را برای $$n$$ عدد تعمیم داد. در این حالت، این نامساوی به شکل زیر خواهد بود:

$$\large { a _ 1 ^ { \large \frac { 1 } { { { p _ 1 } } } \normalsize } a _ 2 ^ { \large \frac { 1 } { { { p _ 2 } } } \normalsize } \ldots a _ n ^ { \large \frac { 1 } { { { p _ n } } } \normalsize } } { \le \frac { { { a _ 1 } } } { { { p _ 1 } } } + \frac { { { a _ 2 } } } { { { p _ 2 } } } + \ldots + \frac { { { a _ n } } } { { { p _ n } } } , }$$

که در آن:

$$\large { { a _ 1 } , { a _ 2 } , \ldots , { a _ n } , { p _ 1 } , { p _ 2 } , \ldots , { p _ n } \gt 0 , } \; \; \; \kern-0.3pt { \frac { 1 } { { { p _ 1 } } } + \frac { 1 } { {{ p_ 2 } } } + \ldots + \frac { 1 } { { { p _ n } } } = 1 .}$$

در صورتی که $${p_1} = {p_2} = \ldots = {p_n} = n$$ باشد، رابطه زیر به دست می‌‌آید:

$$\large \sqrt [ \large n \normalsize ] { {{ a _ 1 } { a _ 2 } \cdots { a _ n } } } \le \frac { { { a _ 1 } + { a _ 2 } + \ldots + { a _ n } } } { n } ,$$

این بدین معنی است که میانگین هندسی $$n$$ عدد نامنفی بزرگ‌تر از میانگین حسابی آن‌ها نیست.

نامساوی هولدر

$$n$$ جفت عدد مثبت $${x_i},{y_i},\,\left( {i = 1, \ldots ,n} \right)$$ را در نظر بگیرید. اگر اعداد $$p$$ و $$q$$ در شرط $${\large\frac{1}{p}\normalsize} + {\large\frac{1}{q}\normalsize} = 1$$ صدق کنند، آنگاه نامساوی هولدر به ازای $$p \gt 1$$ به صورت زیر خواهد بود:

$$\large { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } } { \le { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^ q } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } . }$$

برای اثبات این رابطه، کافی است از نمادگذاری زیر استفاده کنیم:

$$\large { A = \sum \limits _ { i = 1 } ^ n { a _ i ^ p } , } \; \; \; \kern-0.3pt { B = \sum \limits _ { i = 1 } ^ n { b _ i ^ q } . }$$

در این صورت، می‌‌توان نامساوی هولدر را به شکل زیر نوشت:

$$\large \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } \le { A ^ { \large \frac { 1 } { p } \normalsize } } { B ^ { \large \frac { 1 } { q } \normalsize } } .$$

در مرحله بعد، از نامساوی یانگ به فرم زیر استفاده می‌‌کنیم:

$$\large { a ^ { \large \frac { 1 } { p } \normalsize } }{ b ^ { \large \frac { 1 } { q } \normalsize } } \le \frac { a } { p } + \frac { b } { q } .$$

که در آن:

$$\large { a = \frac { { a _ i ^ p } } { A } , } \; \; \; \kern-0.3pt { b = \frac { { b _ i ^ q } } { B } . }$$

با به کار بردن نامساوی یانگ برای هر جفت از اعداد $$a_i$$ و $$b_i$$، داریم:

$$ \large \require {cancel} { \sum \limits _ { i = 1 } ^ n { \frac { { { a _ i } { b _ i } } } { { { A ^ { \large \frac { 1 }{ p } \normalsize } } { B ^ { \large \frac { 1 } { q } \normalsize } } } } } \le \sum \limits _ { i = 1 } ^ n { \left ( { \frac { { a _ i ^ p } } { { p A } } + \frac { { b _ i ^ q } } { { q B } } } \right ) } , \; \; } \Rightarrow { \frac { { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } } } { { { A ^ { \large \frac { 1 }{ p } \normalsize } } { B ^ { \large \frac { 1 } { q } \normalsize } } } } \le \frac { { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } } { { p A } } + \frac { { \sum \limits _ { i = 1 } ^ n { b _ i ^ q } } } { { q B } } , \; \; } \\ \large \Rightarrow { \frac { { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } } }{ {{ A ^ { \large \frac { 1 } { p } \normalsize } } { B ^ { \large \frac { 1 } { q } \normalsize } } } } \le \frac { \cancel { A } }{ { p \cancel { A } } } + \frac { \cancel { B } } { { q \cancel { B } } } = \frac { 1 } { p } + \frac { 1 } { q } = 1 , \; \; } \Rightarrow { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } \le { A ^ { \large \frac { 1 } { p } \normalsize } }{ B ^ { \large \frac { 1 } { q } \normalsize } } , \; \; } \\ \large \Rightarrow { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } \le { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } { \left ( { \sum \limits _ { i = 1 } ^ n { b_ i ^ q } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } \; \; } \kern0pt { \left ( { p > 1 } \right ) . } $$

بدین ترتیب، نامساوی هولدر برای حالت $$p>1$$ اثبات شد. در حالت $$p \lt 1$$ ($$p \ne 0$$) نیز این نامساوی به شکل زیر نوشته می‌‌شود:

$$\large { \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } \ge { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^ q } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } } \; \; \; \kern-0.3pt { \left ( { p \lt 1 , \, p \ne 0 } \right ) . }$$

نامساوی کوشی-شوارتز

نامساوی معروف دیگری به نام نامساوی کوشی-شوارتز وجود دارد که می‌‌توان آن را حالت خاصی از نامساوی هولدر در نظر گرفت. در واقع، با قرار دادن $$p = q = 2$$ در نامساوی هولدر، می‌‌توان این نامساوی را به دست آورد:

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

$$\large \sum \limits _ { i = 1 } ^ n { { a _ i } { b _ i } } \le \sqrt { \sum \limits _ { i = 1 } ^ n { a _ i ^ 2 } } \sqrt { \sum \limits _ { i = 1 } ^ n { b _ i ^ 2 } } .$$

نامساوی مینکوفسکی

نامساوی مینکوفسکی بیان می‌‌کند که برای اعداد مثبت $$a_i$$ و $$b_i$$ رابطه زیر برقرار است:

$$\large {{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } \right)^{\large\frac{1}{p}\normalsize}} }\kern0pt {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}} }\kern0pt {+ {\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)^{\large\frac{1}{p}\normalsize}},}$$

که در آن، $$p<1$$.

این نامساوی نیز از نامساوی هولدر نتیجه می‌‌شود. جمع طرف چپ نامساوی مینکوفسکی را می‌‌توان به صورت زیر نوشت:

$$\large \begin {align*} \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } & = { \sum \limits _ { i = 1 } ^ n { \left ( { { a _ i } + { b _ i } } \right ) { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { p – 1 } } } } \\ & = { \sum \limits _ { i = 1 } ^ n { { a _ i } { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { p – 1 } } } } + { \sum \limits _ { i = 1 } ^ n { { b _ i } { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { p – 1 } } } . } \end {align*}$$

اگر نامساوی هولدر را برای هر یک از جمع‌‌ها به کار ببریم، خواهیم داشت:

$$\large \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } = \sum \limits _ { i = 1 } ^ n { { a _ i } { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { p – 1 } } } \kern0pt { + \sum \limits _ { i = 1 } ^ n { { b _ i } { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { p – 1 } } } } \kern0pt \\ \large { \le { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } }{ \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { \left ( { p – 1 } \right ) q } } } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } } \kern0pt { + { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^p } } \right ) ^{ \large \frac { 1 } { p } \normalsize } } { \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { \left ( { p – 1 } \right ) q } } } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } } \kern0pt \\ \large = { { \left [ { { { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) } ^ { \large \frac { 1 } { p } \normalsize } } + { { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^ p } } \right ) } ^ { \large \frac { 1 } { p } \normalsize } } } \right ] \cdot } \kern0pt { { { \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ { \left ( { p – 1 } \right ) q } } } } \right ) ^ { \large \frac { 1 } { q } \normalsize } } } . } }$$

توجه داشته باشید که در نامساوی هولدر باید شرط زیر برقرار باشد:

$$\large { \frac { 1 } { p } + \frac { 1 } { q } = 1 , \; \; } \Rightarrow { \frac { 1 } { q } = 1 – \frac { 1 } { p } = \frac { { p – 1 } } { p } , \; \; } \Rightarrow { q = \frac { p } { { p – 1 } } . }$$

بنابراین، عبارت قبلی را می‌‌توان به صورت زیر نشان داد:

$$\large { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } } \kern0pt { \le { \left [ { { { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) } ^ { \large \frac { 1 } { p } \normalsize } } + { { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^ p } } \right ) } ^ { \large \frac { 1 } { p } \normalsize } } } \right ] \cdot } \kern0pt { { \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } } \right ) ^ { \large \frac { 1 }{ q } \normalsize } } , } \; \; } \\ \large \Rightarrow { \frac { { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i} } \right ) } ^ p } } } } { { { { \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } } \right ) }^ { \large \frac { 1 } { q } \normalsize } } } } } \kern0pt { \le { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } + { \left ( { \sum \limits _ { i = 1 } ^ n { b _ i ^ p } } \right ) ^ { \large \frac { 1 }{ p } \normalsize } } . }$$

از آنجایی که $$1 – {\large\frac{1}{q}\normalsize} = {\large\frac{1}{p}\normalsize}$$، خواهیم داشت:

$$\large { { \left ( { \sum \limits _ { i = 1 } ^ n { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ p } } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } } \kern0pt { \le { \left ( { \sum \limits _ { i = 1 } ^ n { a _ i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } }\kern0pt { + { \left ( { \sum \limits _ { i = 1 } ^ n { b _i ^ p } } \right ) ^ { \large \frac { 1 } { p } \normalsize } } . }$$

این نامساوی، نامساوی مینکوفسکی برای حالت $$p \lt 1$$ ($$p \ne 0$$) است.

نامساوی مثلثی

نامساوی مثلثی در دو بعد از نامساوی مینکوفسکی به ازای $$n=2$$ و $$p=2$$ به دست می‌‌آید.

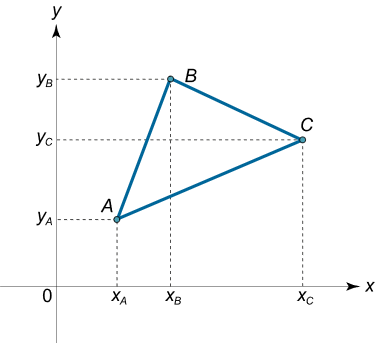
مثلث ABC با رأس‌‌های $$A\left( {{x_A},{y_A}} \right)$$، $$B\left( {{x_B},{y_B}} \right)$$ و $$C\left( {{x_C},{y_C}} \right)$$ را در صفحه $$xy$$ در نظر بگیرید (شکل 7). با قرار دادن $$n=2$$ و $$p=2$$ در نامساوی مینکوفسکی، داریم:

$$\large { \sqrt { \sum \limits _ { i = 1 } ^ 2 { { { \left ( { { a _ i } + { b _ i } } \right ) } ^ 2 } } } } \kern0pt { \le \sqrt { \sum \limits _ { i = 1 } ^ 2 { a _ i ^ 2 } } + \sqrt { \sum \limits _ { i = 1 } ^ 2 { b _ i ^ 2 } } , \; \; } \\ \large \Rightarrow { \sqrt { { { \left ( { { a _ 1 } + { b _ 1 } } \right ) } ^ 2 } + { { \left ( { {a _ 2 } + { b _ 2 } } \right ) } ^ 2 } } } \kern0pt { \le \sqrt { a _ 1 ^ 2 + a _ 2 ^ 2 } + \sqrt { b _ 1 ^ 2 + b _ 2 ^ 2 } . }$$

فرض کنید که اعداد $$a_1$$، $$a_2$$، $$b_1$$ و $$b_2$$ از طریق مختصات رأس‌‌های مثلث به صورت زیر بیان می‌‌شوند:

$$\large { { a _ 1 } = { x _ A } – { x _ B } , } \; \; \; \kern-0.3pt { { a _ 2 } = { y _ A } – { y _ B } , } \; \; \; \kern-0.3pt { { b _ 1 } = { x _ B} – { x _ C } , } \; \; \; \kern-0.3pt { { b _ 2 } = { y _ B } – { y _ C } . }$$

بنابراین، می‌‌توان نوشت:

$$\large { \sqrt { { { \left ( { { x _ A } – \cancel { x _ B } + \cancel { x _ B } – { x _ C } } \right ) } ^ 2 } + { { \left ( { { y _ A } – \cancel { y _ B } + \cancel { y _ B } – { y _ C } } \right ) } ^ 2 } } }\kern0pt \\ \large { \le \sqrt { { { \left ( { { x _ A } – { x _ B } } \right ) } ^ 2 } + { { \left ( { { y _ A } – { y _ B } } \right ) } ^ 2 } } } \kern0pt { + \sqrt { { { \left ( { { x _ B } – { x _ C } } \right ) } ^ 2 } + { { \left ( { { y _ B } – { y _ C } } \right ) } ^ 2 } } }$$

یا

$$\large { \sqrt { { { \left ( { { x _ A } – { x _ C } } \right ) } ^ 2 } + { { \left ( { { y _ A } – { y _ C } } \right ) } ^ 2 } } } \kern0pt \\ \large { \le \sqrt { { { \left ( { { x _ A } – { x _ B } } \right ) } ^ 2 } + { { \left ( { { y _ A } – { y _ B } } \right ) } ^ 2 } } } \kern0pt { + \sqrt { { { \left ( { { x _ B } – { x _ C } } \right ) } ^ 2 } + { { \left ( { { y _ B } – { y _ C } } \right ) } ^ 2 } } . }$$

این نامساوی، نامساوی مثلثی نامیده می‌‌شود و رابطه بین طول اضلاع مثلث را نشان می‌‌دهد:

$$\large \left| { A C } \right | \le \left | { A B } \right | + \left | { B C } \right | .$$

این بدین معنی است که طول هر ضلع مثلث از مجموع طول‌‌های دو ضلع دیگر آن بزرگ‌تر نیست. علامت مساوی در این حالت فقط زمانی امکان‌‌پذیر است که سه نقطه روی یک خط قرار بگیرند.

به طور مشابه، می‌‌توان با استفاده از نامساوی مینکوفسکی، نامساوی مثلثی را در فضای اقلیدسی سه‌‌بعدی به دست آورد. این حالت زمانی اتفاق می‌‌افتد که $$n=3$$ و $$p=2$$ باشد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• نامساوی جنسن (Jensen Inequality) — به زبان ساده
• رسم نامعادلات و نامساوی‌ های خطی — به زبان ساده

^^