مماس دایره چیست و چه ویژگی هایی دارد؟ — به زبان ساده + حل تمرین و مثال

به خطی که دایره را فقط در یک نقطه قطع می‌کند، مماس دایره می‌گویند. مماس در نقطه تماس بر شعاع عمود است. در این مقاله، به معرفی مماس دایره و خواص آن می‌پردازیم. سپس، ضمن اثبات برخی از خواص مماس، چندین مثال متنوع و کاربردی را حل می‌کنیم.

دایره چیست؟

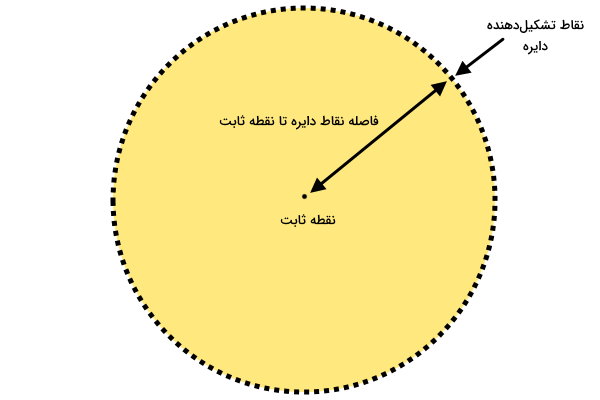
به مجموعه‌ای از نقاط متصل به هم که در فاصله یکسانی از یک نقطه ثابت قرار دارند، دایره می‌گویند.

اجزای دایره چه هستند؟

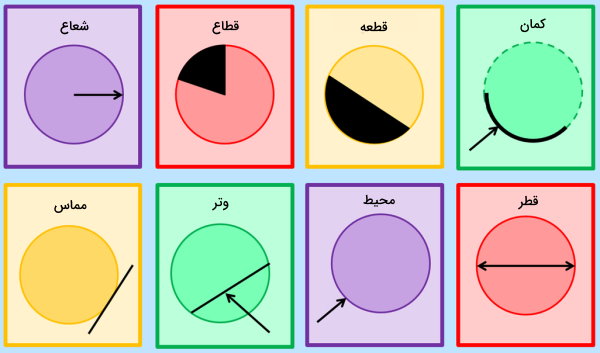
محیط دایره را می‌توان به عنوان مهم‌ترین جزء این شکل هندسی در نظر گرفت. محیط، مجموعه نقاط تشکیل‌دهنده دایره است.

اجزای دیگری مانند مرکز، شعاع، قطر، وتر، کمان، مماس، قطاع و قطعه، با توجه به محیط دایره تعریف می‌شوند.

مماس دایره چیست؟

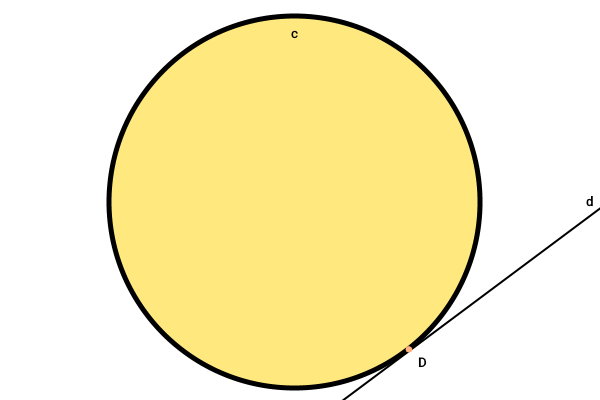
«مماس» (Tangent)، خطی است که دایره را فقط در یک نقطه قطع می‌کند. به محل برخورد مماس به دایره، «نقطه تماس» (Tangency) می‌گویند.

در تصویر زیر، خط d بر دایره c مماس شده است. D، نقطه تماس خط مماس بر دایره را نمایش می‌دهد.

مماس دایره چه ویژگی هایی دارد ؟

برخی از مهم‌ترین ویژگی‌های مماس دایره عبارت هستند از:

• مماس، همواره دایره را در یک نقطه قطع می‌کند.
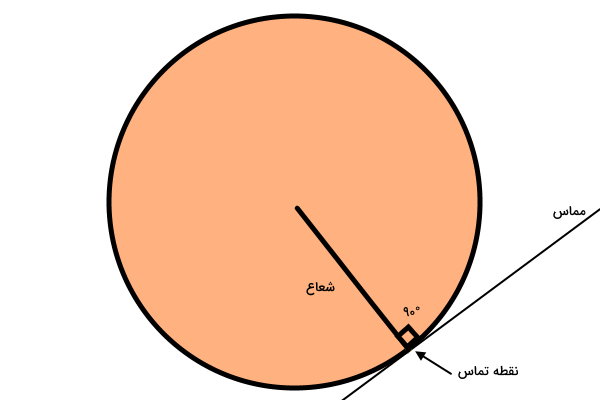
• مماس دایره با شعاع آن در نقطه تماس، زاویه قائمه می‌سازد. به عبارت دیگر، شعاع دایره در نقطه تماس بر خط مماس عمود است.
• از هر نقطه خارج از دایره، می‌توان دو مماس رسم کرد.
• اندازه دو مماس رسم شده از نقطه‌ای در خارج دایره، همواره برابر است.

تعریف هندسی مماس دایره چیست؟

بر اساس تعاریف هندسی، یک خط را مماس دایره می‌نامند، اگر و تنها اگر آن خط بر شعاع رسم شده از نقطه تماس عمود باشد.

طول خط مماس دایره چگونه بدست می آید ؟

طول خط مماس دایره از یک نقطه مشخص تا محل تماس، با استفاده از قضیه فیثاغورس در مثلث‌های قائم الزاویه به دست می‌آید. مراحل محاسبه این اندازه را با حل یک مثال، به طور کامل توضیح می‌دهیم.

مثال 1: محاسبه طول خط مماس

فاصله یک نقطه از مرکز دایره برابر 13 سانتی‌متر و قطر دایره برابر 10 سانتی‌متر است. طول خط مماس از آن نقطه تا محل تماس را حساب کنید.

برای حل این مثال، ابتدا شکل مسئله را رسم می‌کنیم و سپس از خواص مماس و ویژگی‌های دایره برای تعیین اندازه‌های مورد نیاز کمک می‌گیریم.

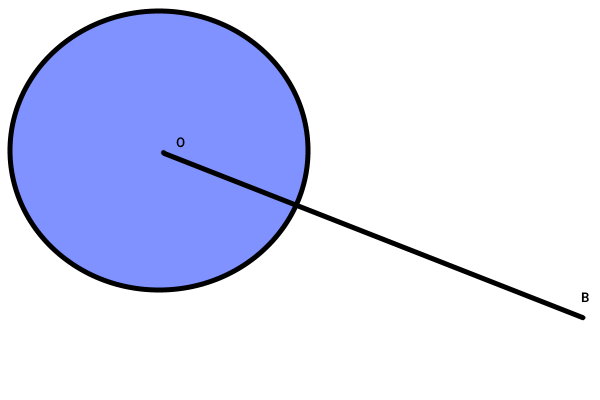
تصویر بالا، ساختار کلی مسئله را نمایش می‌دهد. در این تصویر، نقطه B را به عنوان نقطه شروع مماس و نقطه O را به عنوان مرکز دایره در نظر گرفته‌ایم. از نقطه B، یک خط مماس بر محیط دایره رسم می‌کنیم. محل برخورد این خط را با حرف A نمایش می‌دهیم. یک پاره‌خط نیز از نقطه O تا نقطه A می‌کشیم.

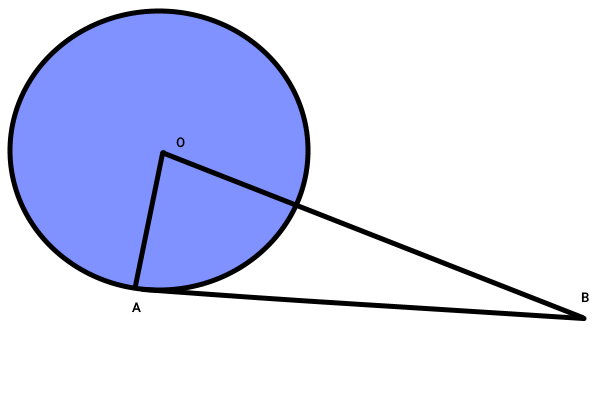
پاره‌خط OA، شعاع دایره است. طول این پاره‌خط، نصف قطر یا 5 سانتی‌متر است. بر اساس ویژگی‌های مماس دایره، OA (شعاع)، در نقطه A (محل تماس) بر BA (خط مماس) عمود خواهد بود. مطابق با صورت مسئله، طول پاره‌خط OB برابر با 13 سانتی‌متر است. اندازه‌های معلوم را بر روی بخش‌های مختلف شکل می‌نویسیم.

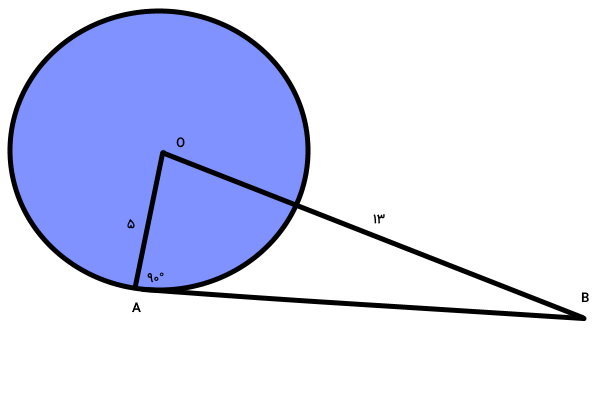
به شکل رسم شده دقت کنید. OB ،OA و BA، یک مثلث قائم الزاویه را تشکیل می‌دهند. در این مثلث، زاویه راس A برابر با 90 درجه است. بنابراین، OB (ضلع مقابل زاویه قائمه)، وتر مثلث قائم الزاویه و دو ضلع دیگر، ساق‌های این مثلث در نظر گرفته می‌شوند. مثلث‌های قائم الزاویه، از قضیه فیثاغورس پیروی می‌کنند. با توجه به این قضیه، مربع وتر با مجموع مربعات ساق‌ها برابر است:

$$c^۲ = a^۲ + b^۲$$

• c: وتر
• a: یکی از ساق‌ها
• b: ساق دیگر

فرمول بالا را بر اساس شکل رسم شده بازنویسی می‌کنیم. به این ترتیب، خواهیم داشت:

$$OB^۲ = OA^۲ + BA^۲$$

• OB: وتر برابر 13 سانتی‌متر
• OA: یکی از ساق‌ها برابر 5 سانتی‌متر
• BA: ساق دیگر (طول مماس دایره تا محل تماس)

اندازه‌های معلوم را درون فرمول قرار می‌دهیم:

$$۱۳^۲ = ۵^۲ + BA^۲$$

$$۱۶۹ = ۲۵ + BA^۲$$

$$BA^۲ = ۱۶۹ - ۲۵$$

$$BA^۲ = ۱۴۴$$

$$BA = \sqrt{۱۴۴}$$

$$BA = ۱۲$$

در نتیجه، طول خط مماس تا محل تماس برابر با 12 سانتی‌متر است.

مثال 2: تعیین اندازه زاویه‌های مثلث با استفاده از خواص مماس

پاره‌خط QP در نقطه P بر دایره مماس شده است. اگر نقطه O، مرکز دایره باشد، اندازه زاویه x چند درجه خواهد بود؟

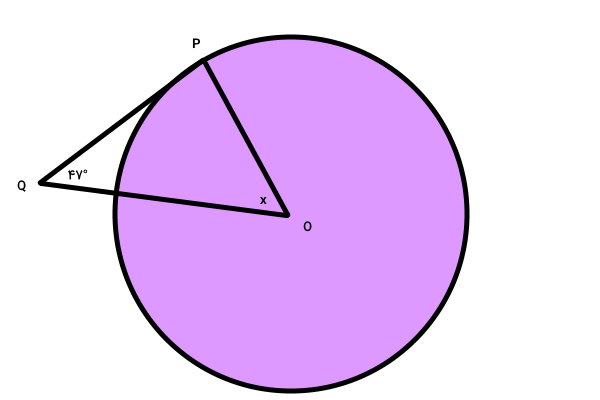
O، مرکز دایره بالا است. بنابراین، OP، شعاع دایره محسوب می‌شود. می‌دانیم که مماس دایره با شعاع آن در محل تماس، زاویه قائمه می‌سازد. از این‌رو، زاویه راس P در مثلث OPQ برابر با 90 درجه است.

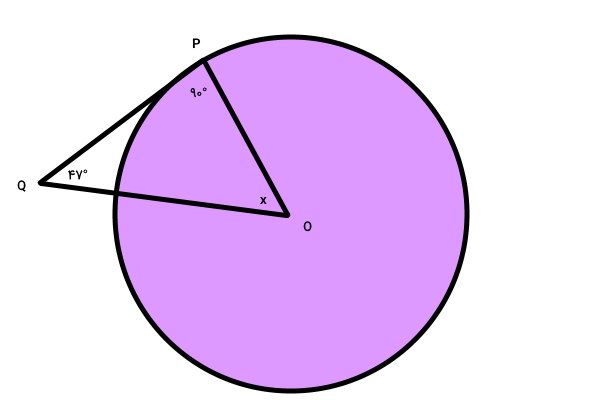
جمع زوایای داخلی مثلث، همواره برابر با 180 درجه است. به همین دلیل، داریم:

$$\hat{O} + \hat{P} + \hat{Q} = ۱۸۰^{\circ}$$

$$\hat{P}$$

زاویه مماس در محل تماس برابر 90 درجه

$$\hat{O}$$

برابر 47 درجه

$$\hat{Q}$$

زاویه‌های معلوم را درون رابطه مجموع زوایای داخلی مثلث قرار می‌دهیم:

$$۴۷^{\circ} + ۹۰^{\circ} + \hat{Q} = ۱۸۰^{\circ}$$

$$۱۳۷^{\circ} + \hat{Q} = ۱۸۰^{\circ}$$

$$\hat{Q} = ۱۸۰^{\circ} - ۱۳۷^{\circ}$$

$$\hat{Q} = ۴۳^{\circ}$$

در نتیجه، زاویه Q برابر با ۴۳ درجه است. در این مثال، مشاهده کردید که یکی از زاویه‌های مثلث OPQ، همواره برابر با 90 درجه خواهد بود. به عبارت دیگر، اگر مماس، شعاع و پاره‌خط بین نقطه‌ای از مماس تا مرکز دایره را رسم کنیم، همیشه یک مثلث قائم الزاویه به وجود می‌آید. از این ویژگی می‌توان در محاسبه اندازه‌های مختلف مماس و دایره بهره گرفت.

دو خط مماس بر دایره

اگر از یک نقطه ثابت، دو خط مماس بر دایره را رسم کنیم، طول هر دو مماس با یکدیگر برابر خواهد بود. بهترین راه برای اثبات برابری اندازه دو مماس، استفاده از هم‌نهشتی مثلث‌ها است.

در هندسه، اگر اندازه تمام ضلع‌ها و زاویه‌های دو شکل با هم برابر باشند، به آن دو شکل، هم‌نهشت می‌گویند. شکل‌های هم‌نهشت را می‌توان با تبدیلاتی مانند انتقال، دوران یا بازتاب، بر روی هم منطبق کرد.

اثبات برابر بودن اندازه دو مماس

شکل زیر را در نظر بگیرید. در این تصویر، دو خط مماس از نقطه ثابت A بر دایره‌ای به مرکز O رسم شده و محیط دایره را نقاط B و C قطع کرده‌اند.

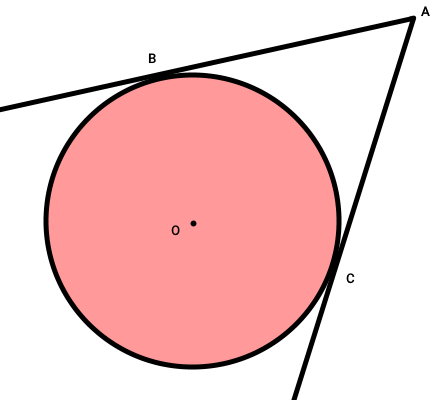
می‌خواهیم ثابت کنیم که طول‌های دو مماس رسم شده برابر هستند. به این منظور، کافی است نشان دهیم که دو پاره‌خط AB و AC، اندازه برابر دارند. برای شروع، از مرکز دایره، دو پاره‌خط تا نقاط B و C رسم می‌کنیم. به این ترتیب، دو پاره‌خط OB و OC به وجود می‌آید.

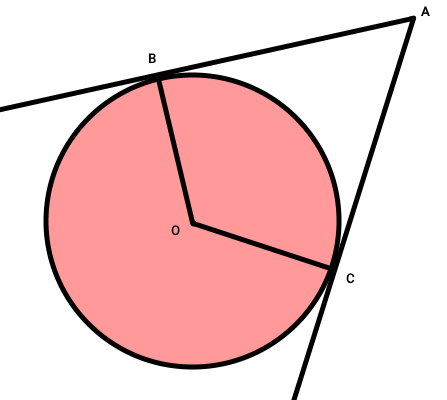
اگر یک پاره خط از نقطه A تا نقطه O‌ رسم کنیم، دو مثلث OAB و OAC تشکیل می‌شود.

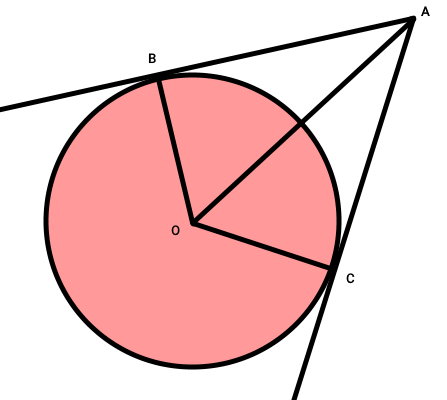
با اثبات هم‌نهشتی مثلث‌های OAB و OAC، برابری دو پاره‌خط AB و AC نیز اثبات می‌شود. OB و OC، شعاع‌های دایره هستند. به این ترتیب، اندازه این ضلع با هم برابر است:

$$OB = OC$$

بر اساس تعریف، شعاع دایره در نقطه تماس بر مماس عمود است. بنابراین، دو زاویه B و C هم‌اندازه و برابر 90 درجه هستند:

$$\hat {B} = \hat {C} = ۹۰^{\circ}$$

دلیل وجود یک زاویه راست (90 درجه)، OAB و OAC، دو مثلث قائم الزاویه محسوب می‌شوند. پاره‌خط OA، وتر این دو مثلث است. از این‌رو می‌توانیم بگوئیم وترهای OAB و OAC هم‌اندازه هستند:

$$OA = OA$$

دو زاویه و ضلع بین (ز ض ز)، دو ضلع و زاویه بین (ض ز ض) و دو سه ضلع (ض ض ض)، به عنوان حالت‌های اصلی هم‌نهشتی مثلث‌ها در نظر گرفته می‌شوند. البته در مثلث‌های قائم الزاویه، اگر وتر و یک ضلع برابر باشند، دو مثلث قائم الزاویه هم‌نهشت خواهند بود. حالت هم‌نهشتی مثلث‌های OAB و OAC نیز همین حالت است. در نتیجه، تمام ضلع‌های زاویه ‌های این دو مثلث، از جمله ضلع‌های AB و AC با هم برابر هستند.

معادله خط مماس بر دایره

معادله دایره‌ای به شعاع r برابر است با:

$$x^۲ + y^۲ = r^۲$$

در معادله بالا، مرکز دایره بر روی مبدا مختصات (0,0) قرار دارد. اگر مرکز دایره، بر روی نقطه دیگری از مختصات قرار داشته باشد، معادله دایره به شکل زیر تغییر می‌کند:

$$(x-x_۱)^۲ + (y-y_۱)^۲ = r^۲$$

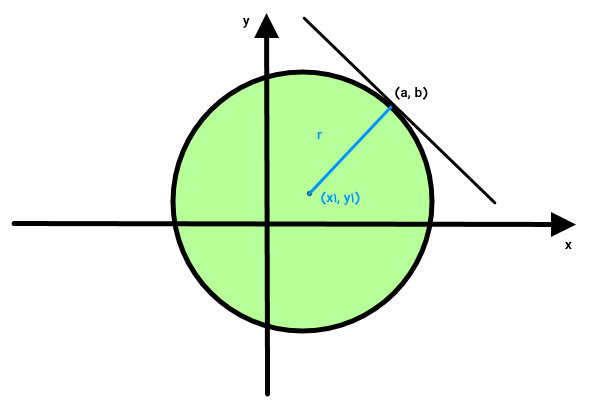
تصویر بالا، یکی از مماس‌های دایره را نمایش می‌دهد که در نقطه (a,b) با محیط برخورد کرده است. معادله این مماس دایره به صورت زیر نوشته می‌شود:

$$y- b = m(x-a)$$

در این معادله، m، شیب یا گرادیان خط مماس و اعداد ثابت a و b، مختصات محل تماس دایره با خط مماس را نمایش می‌دهند. شعاع دایره در نقطه تماس بر خط مماس عمود است. به همین دلیل، شیب خط مماس، از معکوس کردن شیب شعاع دایره به دست می‌آید. برای درک بهتر این موارد، به حل یک مثال می‌پردازیم.

مثال 3: نوشتن معادله خط مماس بر دایره

دایره‌ای به معادله زیر را در نظر بگیرید:

$$x^{۲}+y^{۲}+۴ x-۸ y-۵=0$$

اگر یک خط را در نقطه (۸ ,۵-) به این دایره مماس کنیم، معادله آن چه خواهد بود.

به منظور تعیین معادله مماس، باید مختصات مرکز دایره و شیب شعاع آن نسبت به نقطه تماس را به دست بیاوریم. برای این کار، ابتدا باید معادله دایره را به صورت استاندارد در بیاوریم. شکل استاندارد شده معادله بالا برابر است با:

$$(x+۲)^{۲}+(y-۴)^{۲}=۲۵$$

بر اساس فرم استاندارد معادله دایره، مرکز آن نقطه (۴ ,۲-) خواهد بود.

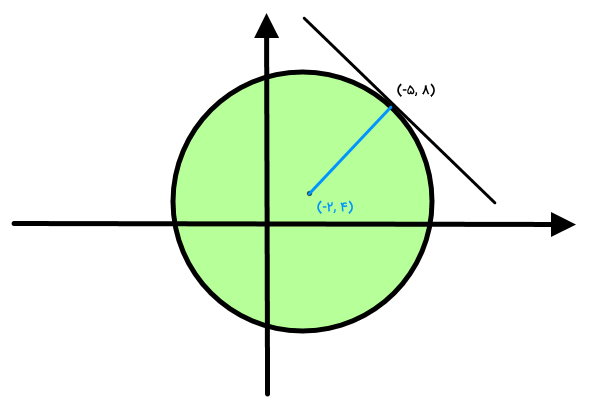
شیب شعاع رسم شده تا نقطه تماس به صورت زیر محاسبه می‌شود:

$$\frac{b-x_۱}{a-y_۱}=\frac{۸-۴}{-۵-(-۲)}=\frac{۴}{-۳}=-\frac{۴}{۳}$$

بنابراین، شیب خط مماس بر دایره، معکوس عدد بالا است:

$$m=\frac{۳}{۴}$$

اکنون، معادله خط مماس را می‌نویسیم و اندازه‌های معلوم را درون آن قرار می‌دهیم:

$$y- b = m(x-a)$$

$$y-۸=\frac{۳}{۴}(x-(-۵))$$

$$۴ y-۳۲=۳ x+۱۵$$

$$۳ x-۴ x+۴۷=0$$

مماس مشترک دایره چیست ؟

اگر خطی به بیش از یک دایره مماس باشد، به آن مماس مشترک می‌گویند. مماس‌های مشترک به دو نوع داخلی و خارجی تقسیم‌بندی می‌شوند.

مماس مشترک داخلی دو دایره

مماس مشترک جانبی یا مماس مشترک داخلی، خطی است که بر دو یا چند دایره مماس می‌شود و خط اتصال مراکز را آن را در فاصله بین دو دایره قطع می‌کند.

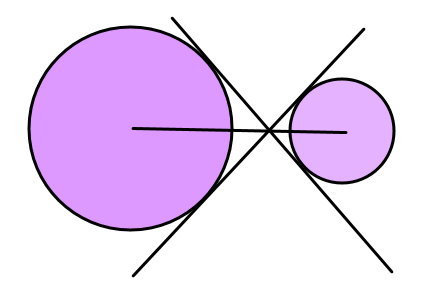
مماس مشترک خارجی دو دایره

مماس مشترک مستقیم یا مماس مشترک خارجی، خطی است که بر دو یا چند دایره مماس می‌شود و امتداد خط اتصال مراکز آن‌ها را قطع می‌کند. تصویر زیر، نمونه‌ای از مماس‌های مشترک خارجی دو دایره را نمایش می‌دهد.

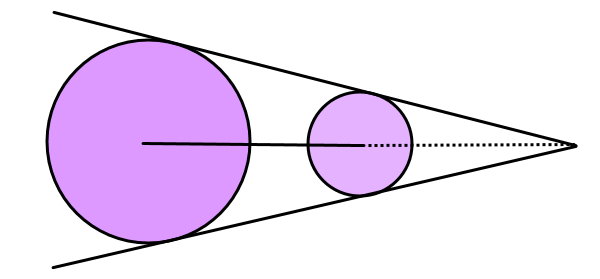
دو دایره مماس بر هم

در برخی از موارد، دو دایره، به اندازه‌ای به هم نزدیک می‌شوند که در یک نقطه همدیگر را قطع می‌کنند. در این حالت، اصطلاحا دو دایره مماس بر هم هستند. این دایره‌ها، دو مماس مشترک خارجی و فقط یک مماس مشترک داخلی دارند. مماس مشترک داخلی دو دایره مماس بر هم از نقطه تماس آن‌ها می‌گذرد.

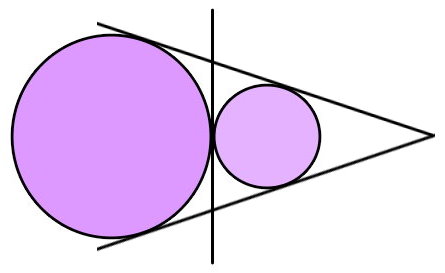
اگر یکی از دایره‌ها در دایره دیگر قرار داشته و بر آن مماس باشد، دو دایره فقط دارای یک مماس مشترک خارجی خواهند بود.

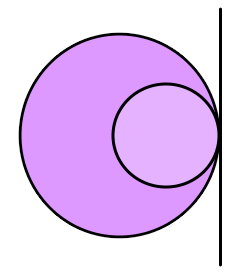
مماس مشترک دو دایره متقاطع

اگر دو دایره در بیش از یک نقطه با هم تقاطع داشته باشند، می‌توان دو مماس مشترک خارجی برای آن‌ها رسم کرد.

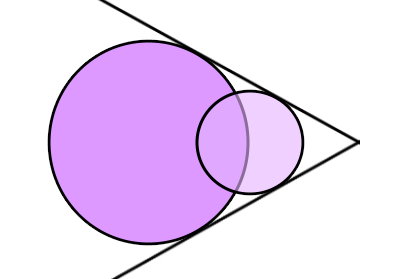
تعداد مماس مشترک دو دایره

به طور کلی، تعداد مماس مشترک‌های دو دایره به صورت زیر تعیین می‌شود:

• دایره‌های مماس
  • مماس درون: یک مماس مشترک خارجی
  • مماس بیرون: یک مماس مشترک داخلی و دو مماس مشترک خارجی
• دایره متقاطع: دو مماس مشترک خارجی
• دایره‌های بدون تماس
  • خارج از هم: دو مماس مشترک داخلی و دو مماس مشترک خارجی
  • داخل هم: بدون مماس مشترک

حل مثال های مماس دایره

در این بخش، به منظور آشنایی بیشتر با خواص و کاربردهای مماس دایره، به حل چند مثال متنوع می‌پردازیم.

مثال 4: محاسبه محیط مثلث با استفاده از ویژگی‌های مماس

تصویر زیر، یک دایره محاط در مثلث را نمایش می‌دهد. با توجه به اندازه‌های معلوم، محیط مثلث را به دست بیاورید.

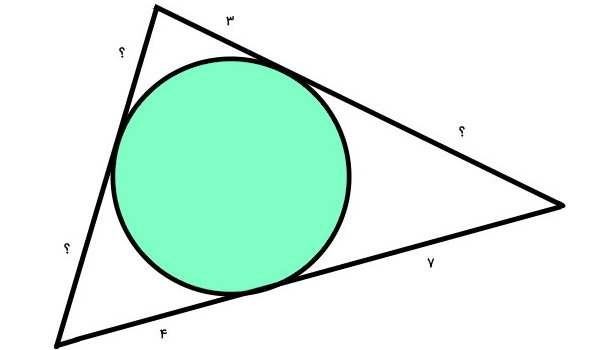
تصویر بالا، شکل یک دایره محاط در مثلث یا مثلث محیط بر دایره است. تمام ضلع‌های مثلث محیطی، بر دایره مماس می‌شود. با استفاده از این ویژگی، می‌توانیم اندازه بخش‌های مجهول را به دست بیاوریم. طول مماس‌های رسم شده از هر راس برابر است.

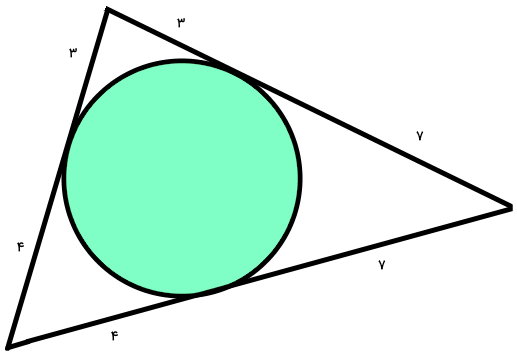
محیط مثلث، از جمع اندازه هر سه ضلع آن به دست می‌آید. در تصویر بالا، اندازه بخش‌های مختلف این ضلع‌ها را تعیین کردیم. بنابراین، داریم:

3 + 3 + 4 + 4 + 7 + 7 = محیط مثلث

28 = محیط مثلث

در نتیجه، محیط مثلث برابر 28 است.

مثال 5: تعیین زاویه های مثلث

در مثلث OPQ، ضلع PQ بر دایره مماس است. اگر نقطه O، مرکز دایره باشد، اندازه زاویه x چقدر خواهد بود؟

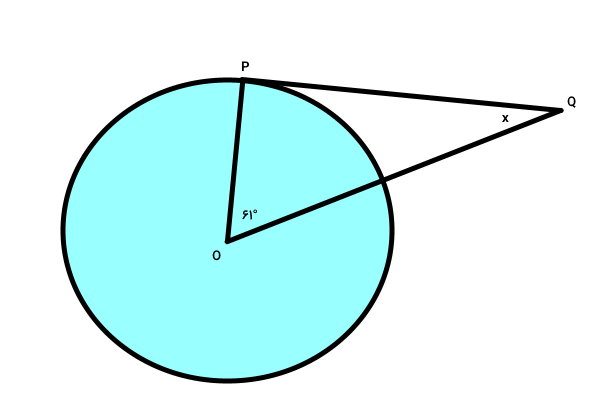
نقطه O مرکز دایره است. بنابراین، ضلع OP، شعاع دایره را نمایش می‌دهد. مماس، در محل تماس با دایره ب شعاع آن عمود می‌شود. بنابراین، زاویه راس P در مثلث برابر 90 درجه است. مطابق با قانون جمع زوایای داخلی در مثلث‌ها داریم:

$$\hat {P} + \hat {O} +\hat {Q} = ۱۸۰^{\circ}$$

با توجه به شکل، اندازه‌های معلوم را در رابطه بالا قرار می‌دهیم:

$${۹۰^{\circ}} + {۶۱^{\circ}} + {x} = ۱۸۰^{\circ}$$

$${x} = ۱۸۰^{\circ} - {۹۰^{\circ}} - {۶۱^{\circ}}$$

$${x} = {۲۹^{\circ}}$$

در نتیجه، زاویه خواسته شده برابر 61 درجه است.

مثال 6: محاسبه شعاع دایره از روی طول مماس

فاصله ابتدای خط مماس بر یک دایره تا نقطه تماس برابر 12 و فاصله آن تا مرکز دایره برابر 15 است. شعاع دایره را حساب کنید.

به خاطر داشته باشید که طول خط مماس تا نقطه تماس، فاصله نقطه ابتدایی خط مماس تا مرکز دایره و شعاع دایره، همیشه یک مثلث قائم الزاویه را تشکیل می‌دهند. در این مثلث، رابطه زیر برقرار است:

$$c^۲ = a^۲ + b^۲$$

• c: فاصله نقطه ابتدایی خط مماس تا مرکز دایره برابر 15
• a: طول خط مماس تا محل تماس برابر 12
• b: شعاع دایره

مقادیر معلوم را درون رابطه بالا قرار می‌دهیم:

$$۱۵^۲ = ۱۲^۲ + b^۲$$

$$b^۲ = ۱۵^۲ - ۱۲^۲$$

$$b^۲ = ۲۲۵ - ۱۴۴$$

$$b^۲ = ۸۱$$

$$b = \sqrt {۸۱}$$

$$b = ۹$$

در نتیجه، شعاع دایره برابر ۹ است.

مثال 7: محاسبه فاصله بین مراکز دو دایره از روی مماس مشترک

پاره خط CD، مماس مشترک دو دایره نمایش داده شده در تصویر زیر است. با توجه به اطلاعات موجود، فاصله بین شعاع‌های دو دایره را به دست بیاورید.

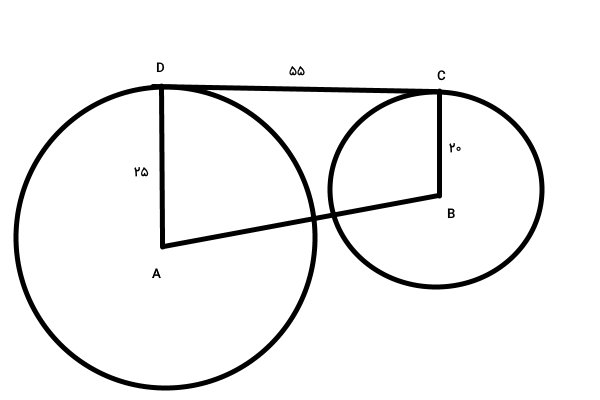
در تصویر بالا، پاره‌خط AB، فاصل بین مراکز دو دایره را نمایش می‌دهد. اگر از نقطه B، خطی را بر پاره خط AD عمود کنیم، یک مستطیل (BEDC) و یک مثلث قائم الزاویه (ABE) تشکیل می‌شود.

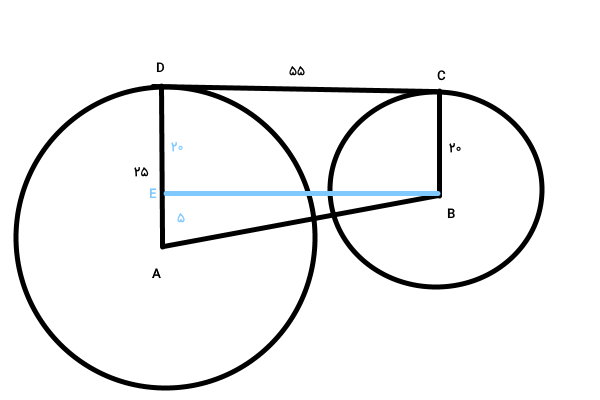
پاره‌خط AB، وتر مثلث قائم الزاویه ABE است. بنابراین داریم:

$$AB^۲=AE^۲+BE^۲$$

$$AB^۲=۵۵^۲+۵^۲$$

$$AB^۲=۳۰۲۵+۲۵$$

$$AB^۲=۳۰۵۰$$

$$AB=\sqrt{۳۰۵۰}$$

$$AB=۵\sqrt{۱۲۲}$$

سوالات متداول در رابطه با مماس دایره

در این بخش، به برخی از سوالات مرتبط با مماس دایره، به طور خلاصه پاسخ می‌دهیم.

تعریف خط مماس بر دایره چیست ؟

اگر یک خط و دایره، تنها یک نقطه مشترک داشته باشند، می‌گوییم خط بر دایره مماس است.

از هر نقطه خارج از دایره چند مماس می‌توان رسم کرد؟

از هر نقطه خارج از دایره، حداکثر دو مماس قابل رسم است.

حالت هم‌نهشتی برابر بودن دو مماس دایره چیست؟

بر اساس حالت هم‌نهشتی وتر و یک ضلع (ساق) در مثلث‌های قائم‌الزاویه می‌توان اثبات کرد که دو مماس دارای نقطه شروع مشترک، با هم برابر هستند.

دایره چند مماس دارد؟

هر دایره می‌تواند بی‌نهایت مماس داشته باشد.

دو دایره چند مماس مشترک دارند؟

با توجه به شعاع و مختصات مرکز، دو دایره می‌توانند حداکثر چهار مماس مشترک و حداقل صفر مماس مشترک داشته باشند.

زاویه بین دو خط مماس بر دایره چگونه بدست می آید؟

زاویه بین دو خط مماس بر دایره برابر حاصلضرب تانژانت معکوس شیب یکی از مماس‌ها در دو است.