عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده

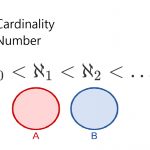
در نظریه مجموعه‌ها (Set Theory)، مفهوم عدد اصلی (Cardinality) یا کاردینالیتی برای یک مجموعه تعریف می‌شود. این عدد برای یک مجموعه متناهی (Finite Set) بیانگر تعداد اعضای آن است. این موضوع ساده، زمانی که مجموعه‌ها نامتناهی شده، مشکل شده و امکان مقایسه مجموعه‌ها را با توجه به تعداد اعضای آن‌ها مشکل می‌سازد. به این ترتیب بحث مربوط به عدد اصلی مجموعه یا کاردینالیتی مجموعه‌ها، یکی از مسائلی است که امکان مرتب‌سازی مجموعه‌ها را براساس تعداد اعضای آن‌ها فراهم می‌سازد.

برای آشنایی بیشتر با اصطلاحات مطرح شده در این نوشتار بهتر است ابتدا مفاهیم مربوط به مجموعه‌ها در نوشتارهای مجموعه ها در ریاضیات – مفاهیم پایه و اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب اعداد گویا — به زبان ساده و اعداد صحیح — به زبان ساده نیز خالی از لطف نخواهد بود.

عدد اصلی مجموعه یا کاردینالیتی

در ریاضیات، عدد اصلی مجموعه به صورت تعداد عناصر آن مجموعه مشخص می‌شود. برای مثال عدد اصلی برای مجموعه متناهی $$A = \{2 , 6, 8\}$$‌ برابر است با ۳ زیرا مجموعه $$A$$ دارای سه عضو است.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

در اواخر قرن نوزدهم عدد اصلی برای مجموعه‌های نامتناهی تبدیل به یک مسئله برای دانشمندان و ریاضیدانان شد. این موضوع بخصوص توجه «جورج کانتور» (George Cantor) و «ریچاد ددکیند» (Richard Dedekind) را به خود جلب کرد.

آنان برای نمایش دادن تعداد اعضای یک مجموعه نامتناهی از نام‌گذاری استفاده کردند و بر این اساس توانستند رابطه بین تعداد اعضای دو مجموعه نامتناهی را مشخص کنند.

نکته: گاهی برای نمایش عدد اصلی یا کاردینالیتی مجموعه $$A$$ از نمادهایی دیگری نیز استفاده می‌کنند. این نمادها در ادامه معرفی شده‌اند. بدیهی است به کار بردن هر یک از آن‌ها معادل با عدد اصلی مجموعه $$A$$ است.

$$\large \#A, \;\; n(A), \;\;\; \operatorname{card} (A) , \;\; |A|$$

عدد اصلی مجموعه و رابطه ترتیبی

هر چند محاسبه عدد اصلی برای یک مجموعه متناهی به سادگی صورت می‌گیرد ولی انتظار می‌رود که رابطه‌ای که بین اعداد اصلی چنین مجموعه‌هایی وجود دارد در رابطه ترتیبی روی عدد اصلی برای مجموعه‌های نامتناهی نیز صادق باشد. به این ترتیب تعریف‌ها زیر برای نشان دادن رابطه ترتیبی بین مجموعه‌های نامتناهی و اعداد اصلی آن‌ها پدید آمد.

تعریف تساوی بین عدد اصلی دو مجموعه

دو مجموعه $$A$$ و $$B$$ را در نظر بگیرید. عدد اصلی مجموعه $$A$$ را با $$|A|$$ و عدد اصلی مجموعه $$B$$‌ را با $$|B|$$ نشان می‌دهیم. دو عدد اصلی این دو مجموعه را برابر می‌گوییم اگر بین اعضای این دو مجموعه بتوان یک تناظر یک به یک (One to One Correspondence) ایجاد کرد.

این امر به این معنی است که بتوان رابطه‌ای از $$A$$ به $$B$$ «پوشا» (Onto) و «یک به یک» (One to One) پیدا کرد که هر عضو از مجموعه $$A$$ را فقط به یک عضو از مجموعه $$B$$ برده و برعکس هر عضو از مجموعه $$B$$ را به فقط یک عضو از مجموعه $$A$$ مرتبط کند. معمولا چنین رابطه‌ای را «دوسویی» (Bijective) می‌نامند. واضح است که تابع دوسویی، وارون‌پذیر (Invertiable) است.

چنین مجموعه‌هایی را «هم‌توان» (Equipotent) یا «هم‌عدد» یا «هم‌شمار» (Equinumerosity) می‌نامند و می‌نویسند:

$$\large |A| = |B| \; \rightarrow \;  A \sim B$$

برای مثال با توجه به رابطه $$y = 2x$$ و با توجه به تعلق مقادیر $$x$$ به مجموعه اعداد طبیعی، به راحتی هم‌توان بودن بین مجموعه اعداد زوج و اعداد طبیعی با توجه به تعریف ارائه شده، نشان داده می‌شود. این امر در تصویر ۲ نشان داده شده است.

تعریف کوچکتر یا مساوی بودن عدد اصلی مجموعه

اگر رابطه مجموعه $$A$$ به $$B$$ یک رابطه یک به یک باشد، آنگاه بین عدد اصلی آن‌ها رابطه زیر نوشته می‌شود.

$$\large  | A |  \leq | B |$$

تعریف کوچکتر بودن عدد اصلی مجموعه

عدد اصلی مجموعه $$A$$ را کمتر اکید از عدد اصلی مجموعه $$B$$ گویند اگر رابطه از $$A$$ به $$B$$ فقط یک رابطه یک به یک بوده و از $$A$$ به $$B$$، پوشا نباشد.

برای مثال مجموعه اعداد طبیعی ($$N$$) را در نظر بگیرید. عدد اصلی این مجموعه نسبت به عدد اصلی مجموعه توانی اعداد طبیعی ($$P(N)$$) که شامل همه زیرمجموعه‌های اعداد طبیعی است، کوچکتر اکید است.

فرض کنید رابطه مربوطه به صورت $$g(n) = \{n\}$$ باشد که از مجموعه اعداد طبیعی ($$N$$) به مجموعه توانی اعداد طبیعی نگاشت عناصر را انجام می‌دهد. از آنجایی که این رابطه، یک به یک بوده ولی پوشا نیست، خواهیم داشت:

$$\large |\ N \ | < | \ P(N) \ |$$

این امر در تصویر ۳ به خوبی دیده می‌شود.

در تصویر ۲، مقادیری روی قطر اصلی تصویر دیده می‌شوند که درون مجموعه $$T$$ قرار ندارند و این امر ناقض رابطه یک به یک بین این دو مجموعه هستند. اعداد قرمز رنگ در قطر اصلی تصویر، مقادیری از توابع $$f$$ را نشان می‌دهد که مجموعه $$T$$ قرار نداشته و مجموعه عناصر $$T$$ وارون نگاشت از مجموعه توانی به مجموعه اعدادطبیعی نیست.

به همین روش می‌توان نشان داد که عدد اصلی مجموعه اعداد طبیعی از مجموعه اعداد حقیقی کوچکتر اکید است. این امر توسط «عناصر قطری کانتور» (Cantor's Diagonal Argument) یا «اثبات اولین شمارش‌ناپذیر کانتور» (Canrtor's First Uncountability Proof) نشان داده می‌شود.

نکته: توجه دارید که گزاره‌های گفته شده، صرفا یک تعریف هستند و احتیاجی به اثبات ندارند.

اگر بین دو مجموعه $$A$$ و $$B$$ رابطه $$|A| \leq | B|$$ و $$|B| \leq |B|$$ برقرار باشد می‌توان نتیجه گرفت که $$|A| = |B|$$. این گزاره را به صورت اصل انتخاب (Axiom of Choice) می‌شناسند.

$$\large |A| \leq |B| \wedge |B| \leq |A | \; \rightarrow \; |A| = | B|$$

عدد اصلی مجموعه

بنا به تعریف‌هایی که در قسمت قبل ارائه شد، نحوه مرتب‌سازی اعداد اصلی مجموعه‌ها مشخص شد، ولی مبنای محاسبه عدد اصلی به طور واضح گفته نشد. در این قسمت با شیوه محاسبه عدد اصلی مجموعه بیشتر آشنا خواهیم شد.چ

فیلم آموزش ریاضیات گسسته – جامع و به زبان ساده در فرادرس

کلیک کنید

اصطلاحاً دو مجموعه را هم‌شمار (Equinumerosity) می‌گویند، اگر عدد اصلی آن‌ها برابر باشد. این تساوی به صورت یک رابطه هم‌ارزی در کلاس همه مجموعه‌ها تعریف می‌شود. کلاس‌های هم‌ارزی برای مجموعه $$A$$، شامل همه مجموعه‌هایی است که عدد اصلی آن‌ها با $$A$$ برابر است. به این ترتیب با دو شیوه عدد اصلی یک مجموعه را تعریف می‌کنیم.

• عدد اصلی مجموعه $$A$$، توسط کلاس هم‌ارزی آن تحت رابطه هم‌شمار، تعریف می‌شود. به این معنی که عدد اصلی کلاس‌های هم‌ارز با $$A$$، عدد اصلی مجموعه $$A$$ را تعیین می‌کنند.
• برای هر کلاس هم‌ارزی، یک مجموعه به عنوان معرف (Representative set) تعیین می‌شود. معمولا مجموعه معرف کلاس هم‌ارزی را مجموعه‌ای انتخاب می‌کنند که ویژگی‌های آن شناخته شده‌تر باشد. عدد اصلی چنین مجموعه‌ای را «مقدار اولیه کلاس هم‌ارزی» (Initial Ordinal in class) می‌نامند. این بیان برای عدد اصلی، به عنوان تعریف معمول در نظریه مجموعه‌ها به کار می‌رود.

بنا به «اصل موضوع انتخاب» (Axiom if Choice)، اعداد اصلی مجموعه‌های بی‌نهایت بوسیله رابطه زیر مشخص و تعیین می‌شوند.

$$\large \aleph _{0}<   \aleph _{1} <\aleph _{2} < \ldots$$

نکته: نماد $$\aleph_0$$ را به صورت «الف-صفر» (Aleph_Null) می‌خوانیم. $$\aleph$$ اولین حرف از زبان عبری است.

برای هر ترتیب $$\alpha$$، مقدار $$\aleph_{\alpha+1}$$ کوچکترین عدد اصلی بزرگتر از $$\aleph_{\alpha}$$ است.

طبق قرار داد ساده‌ترین و معمول‌ترین مجموعه نامتناهی شمارش‌پذیر را اعداد طبیعی (Natural Numbers) در نظر می‌گیریم و عدد اصلی را برای آن به شکل $$\aleph_0$$ نشان می‌دهیم. از طرفی عدد اصلی برای مجموعه اعداد حقیقی را به شکل $$\mathfrak {c}$$ مشخص می‌کنند که گاهی به آن «عدد اصلی پیوستار» (Cardinality of the continuum) نیز گفته می‌شود.

کانتور  (G. Cantor) نشان داد که عدد اصلی اعداد حقیقی بزرگتر از عدد اصلی اعداد طبیعی است. رابطه بین عدد اصلی این دو مجموعه به صورت زیر بیان می‌شود.

 $$\large { \displaystyle { \mathfrak {c}} = 2^{\aleph _{0}}}$$

البته این رابطه برای زیر مجموعه‌هایی از مجموعه اعداد طبیعی نیز صادق است. با توجه به فرضیه پیوستار (continuum hypothesis) می‌توان گفت:

$$\large \aleph_1 = 2 ^{\aleph_0}$$

این رابطه نشان می‌دهد که کوچکترین عدد اصلی که از $$\aleph_0$$ بزرگتر است همان $$2^{\aleph_0}$$ است و هیچ عدد اصلی بین این دو مقدار وجود ندارد. این موضوع (فرضیه پیوستار) را به بیان مجموعه‌ها به صورت زیر مشخص می‌کنیم.

• هیچ مجموعه‌ای وجود ندارد که عدد اصلی آن از اعداد طبیعی بزرگتر بوده و از عدد اصلی اعداد حقیقی کوچکتر باشد.

با توجه به مفهوم عدد اصلی و نحوه ترتیب بین مقادیر اعداد اصلی و فرضیه پیوستار، مجموعه‌های متناهی، شمارا و شمارش‌ناپذیر (ناشمارا) در ادامه تعریف می‌شوند.

مجموعه‌های متناهی، شمارا و ناشمارا

با فرض صحیح بودن اصل موضوع انتخاب، همچنین در نظر گرفتن سه وضعیت برای اعداد اصلی یعنی برابری، بزرگتر یا کوچکتر بودن که در قسمت قبلی بیان شد، تعریف‌ و مفهوم مجموعه‌های متناهی، شمارا و ناشمار را مشخص می‌کند.

• هر مجموعه‌ای مثل $$X$$ با عدد اصلی کوچکتر از عدد اصلی مجموعه اعداد طبیعی، یک مجموعه متناهی (Finite Set) است.

$$\large |X| < |\;N\;| = \aleph_0$$

• مجموعه‌ $$X$$ با عدد اصلی برابر با عدد اصلی اعداد طبیعی، را شمارا یا «شمارای نامتناهی» (Countably Infinite) می‌نامند.

$$\large |X| = |\;N\;| = \aleph_0$$

• مجموعه‌ای با عدد اصلی بزرگتر از عدد اصلی اعداد طبیعی، را «مجموعه ناشمارا» (Uncountable) می‌نامیم. به این ترتیب اگر $$X$$ یک مجموعه ناشمارا باشد، خواهیم داشت:

$$\large |X| > |\;N\;| = \aleph_0$$

برای مثال، مجموعه اعداد حقیقی ($$R$$) را در نظر بگیرید که دارای عدد اصلی بزرگتری از اعداد طبیعی است. چنین مجموعه‌ای، ناشمارا است، زیرا:

 $$\large | R | = { \displaystyle {\mathfrak {c}}}> | \;N\ ;| = \aleph_0$$

خصوصیات عدد اصلی مجموعه

در این بخش می‌خواهیم بعضی از خصوصیات عدد اصلی مجموعه را مشخص کنیم.

• اگر $$X$$ و $$Y$$ مجموعه‌هایی به صورت $$X = \{a,b,c\}$$ و $$Y = \{apples,oranges,peaches\}$$ باشند، آنگاه

$$\large | X | = | Y |$$

زیرا می‌توان یک رابطه یک به یک و پوشا (One to One Correspondence) به صورت زیر بین آن‌ها برقرار کرد.

$$\large R = \{ (a,apple), (b,oranges), (c,peaches) \}$$

• اگر بین عدد اصلی دو مجموعه $$X$$ و $$Y$$ رابطه $$|X| < |Y|$$ باشد، آنگاه مجموعه‌ای مانند $$Z$$ وجود دارد که $$|Z| = |X|$$ و در نتیجه $$Z \subseteq Y$$.
• اگر $$| X | \leq | Y |$$ و $$| Y | \leq | X |$$، آنگاه $$| X | = | Y |$$. این تساوی حتی برای اعداد اصلی مجموعه‌های نامتناهی نیز برقرار است. این رابطه به «قضیه کانتور-برنشتاین-شرودر» ( Cantor–Bernstein–Schroeder theorem) معروف است.
• اگر $$X$$ و $$Y$$ دو مجموعه مجزا (Disjoint sets) بوده که دارای هیچ عضو مشترکی نباشند، آنگاه

$$\large | X \cup Y | = | X | + | Y |$$

• بین عدد اصلی اشتراک و اجتماع دو مجموعه رابطه زیر برقرار است.

$$\large | X \cup Y | + | X \cap Y | = | X | + | Y |$$

خلاصه و جمع‌بندی

در این نوشتار با مفهوم عدد اصلی مجموعه‌ها به عنوان یکی از مفاهیم مربوط به نظریه اعداد آشنا شدیم. مفاهیمی مانند بخش‌پذیری، اعداد اول و هم‌نهشتی از موضوعاتی دیگری هستند که در نظریه اعداد به کار گرفته می‌شوند. عدد اصلی برای مجموعه‌ها این امکان را می‌دهد که مجموعه‌ها را برحسب تعداد اعضای آن‌ها، مرتب کنیم. به این ترتیب بزرگی مجموعه‌ها قابل تعیین خواهد شد. این کار حتی برای مجموعه‌هایی که بی‌نهایت عضو دارند امکان پذیر است. برای مثال با استفاده از قضیه‌هایی، امکان مقایسه تعداد اعضای مجموعه اعداد حقیقی و اعداد طبیعی وجود دارد. براین اساس می‌توان تعریفی برای مجموعه‌های متناهی، شمارش‌پذیر و شمارش‌ناپذیر ارائه داد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر که مرتبط با موضوع این نوشتار هستند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• آموزش ریاضیات مهندسی
• تقسیم عدد صحیح — به زبان ساده
• الگوریتم تقسیم اعداد — از صفر تا صد
• قواعد بخش پذیری یا عاد کردن — به زبان ساده

^^